由一道模考题浅议求二元最值的多种解答策略

王海阔 杜海洋

(1.四川省成都市龙泉驿区教育科学研究院 2.四川省成都经济技术开发区实验中学校)

在高三复习中,我们经常遇到含有两个参变量的代数式求值或值域问题,难度颇大,技巧性较强.笔者发现大部分学生找不到这类问题具体的解答思路,尤其挖掘不出不同题型间的内在联系与区别.本文结合一道经典问题谈谈求解二元代数式最值问题的几种常用方法,以期帮助读者更好地理解和掌握解决此类问题的方法及各种方法之间的联系和区别.

1 试题呈现

题目已知正数x,y满足x＋4y＝x2y3,则的最小值为________.

2 试题解答

据统计,此题得分率极低.大部分学生认为此题可转化为基本不等式求最值.式子含有双变量,与以往所遇到的基本不等式试题结构也没有明显区别,主要是变量次数不一致,导致式子结构变形过程转化难度增大.作为压轴小题,笔者认为此题保持短小精悍风格,堪称经典,这样的试题能给人以启迪,散发着其独特的魅力.研究考题本应成为教师教学研究的常规工作,下面笔者从不同的角度解答这道检测题.

解法1 (二元化一元+均值不等式)

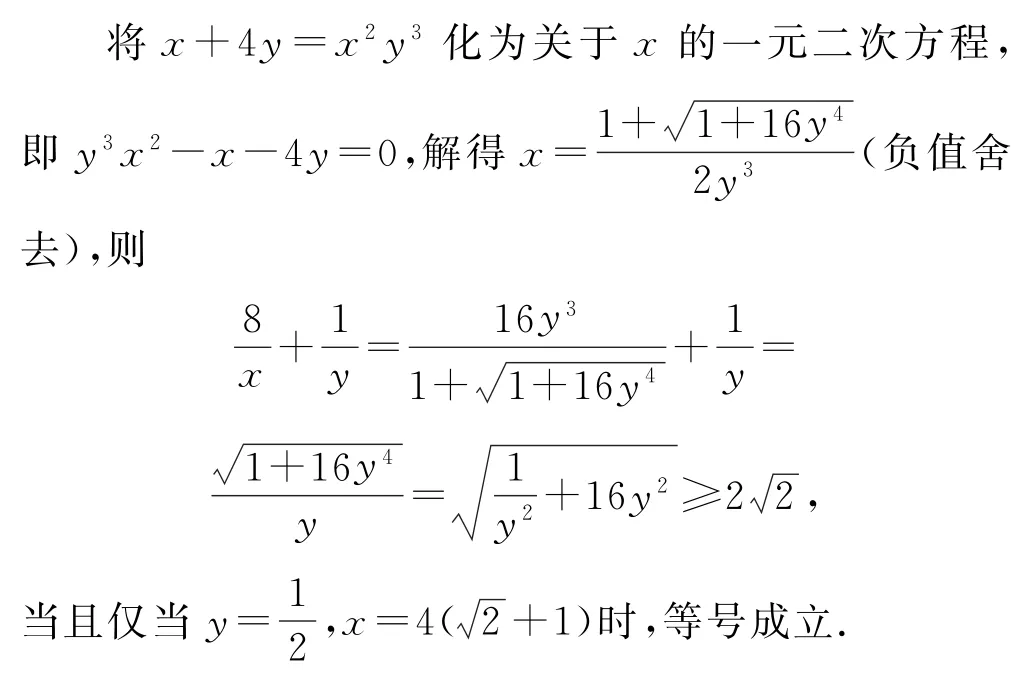
点评对于二元问题,能利用消元法处理的不妨试试消元,将其转化为一元函数问题,退一步讲可以采用求导进行求值,所以遇到这类题根本不用惧怕.此消元策略属于这类问题的通法,即当所求最值的代数式中的变量比较多时,通常考虑利用已知条件消去部分变量后,凑出“和为常数”或“积为常数”,最后利用基本不等式求最值.常见这类题含二次型较多,部分题的前提条件是关于一元二次方程型,可以利用求根公式进行求解.

解法2 (二元化一元+判别式)

点评将所求代数式赋值,这样目标代数式就变成方程组的形式,再将其与已知等式相结合进行消元化为一元二次方程,根据方程有根,利用判别式的取值范围求出最值,这体现了代数式与方程转化与化归策略.

解法3 (二元化一元+基本不等式)

同解法2可得16y4－k2y2＋1＝0,参变分离得

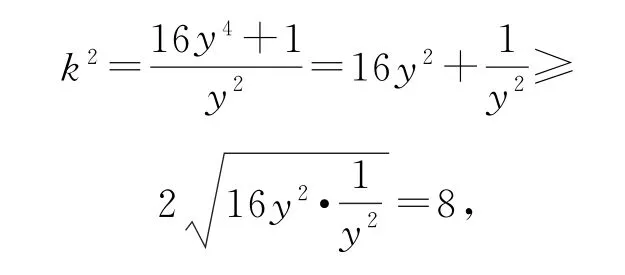
点评此解法利用参变分离,将所求参数用已知变量的函数表示,再结合式子结构特点采用基本不等式或导数进行求解.

解法4 (化齐次+基本不等式)

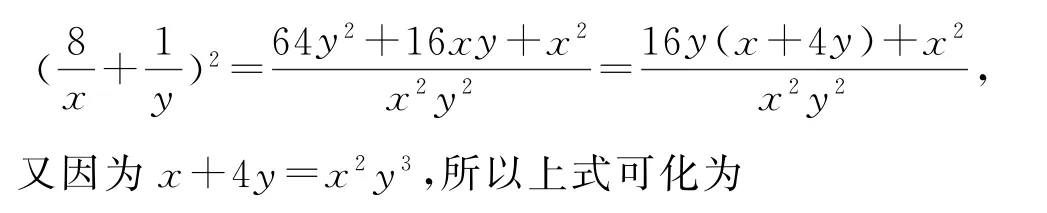
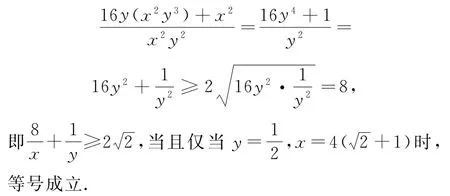
点评此解法利用条件与目标式子的结构特征,将目标式子的指数向条件靠拢,即齐次化策略,再利用已知条件进行整体替换.尤其对于多变量这类题,一般可用整体代换消参求解,平时做题要多领悟总结.

解法5 (拼凑法+基本不等式)

因为

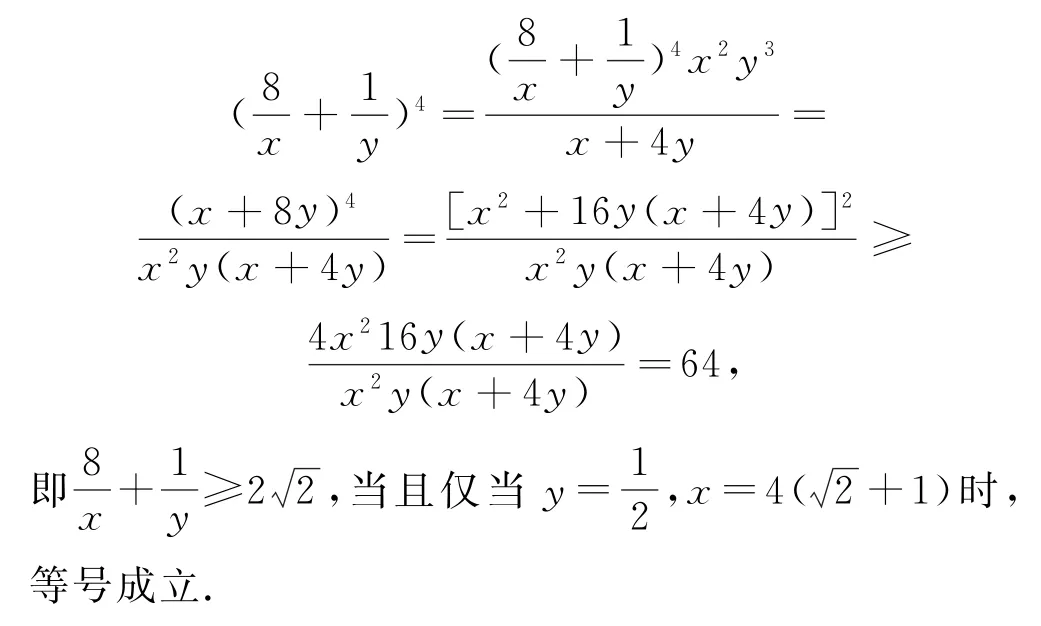
点评利用基本不等式求最值的关键是将相关代数式进行适当的变形,通过添项、拆项等方法凑成“和为定值”或“积为定值”的形式,然后利用基本不等式求解最值.拼凑法的实质是对代数式进行灵活变形,拼系数、凑常数是关键.

解法6 (积换元+基本不等式)

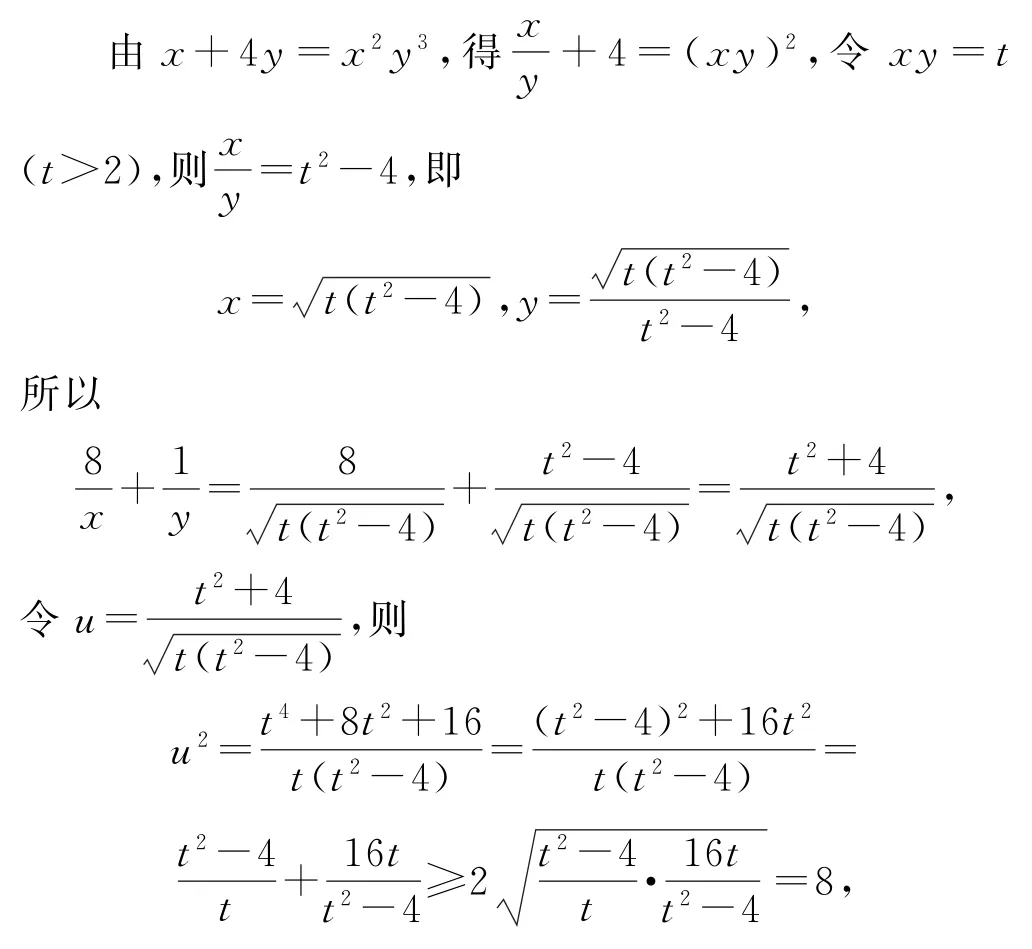
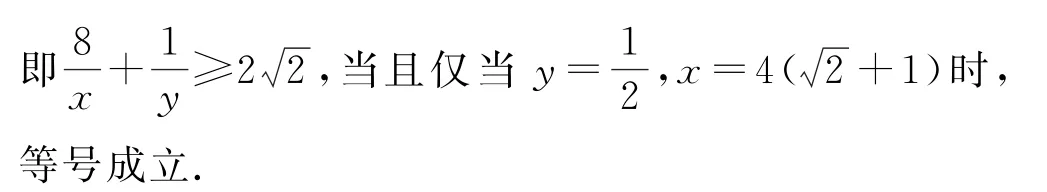
点评当出现或可以化为形如由两个字母如x,y组成的对称式时,我们就可以将代数式用基本对称式x＋y,xy表示出来,即称x＋y,xy为辅助元,这种方法称为和(积)换元.运用和(积)换元法可化简求值、因式分解解方程(组),还可以证明命题,解答某些压轴题和某些数学竞赛题.

解法7 (倒数换元+基本不等式)

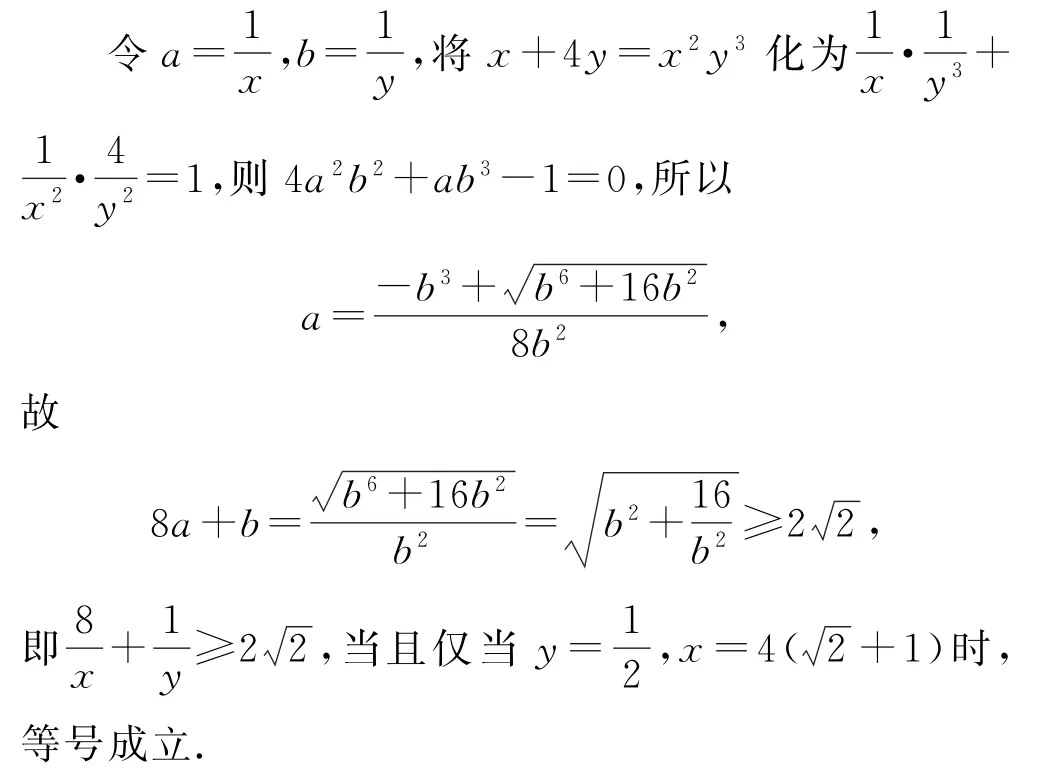
点评倒数法是换元法的一种,先将题中的倒数用整式的字母代替,再将其转化成整式方程并求出整式的解,主要在分式结构中可转化为整式,此解法也称双换元法,即根据多项式的特征用两个字母(元)分别代换原多项式的代数式.

解法8 (局部、整体换元+根与系数的关系)

点评本解法本质上与解法2一样,无非是要实现多次换元,利用换元法得到关于a的方程a2－t2a＋16＝0有两个正实根,再利用根与系数的关系求解.

3 变式训练

变式已知正数a,b,且ab－a－2b＝0,求＋b2的最小值_________.

解法1 (基本不等式+二次函数)

解法2 (消元策略+基本不等式)

当且仅当t＝1时,等号成立.

解法3 (三角换元+基本不等式)

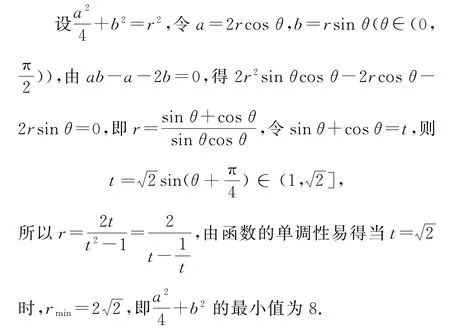
解法4 (商换元+基本不等式)

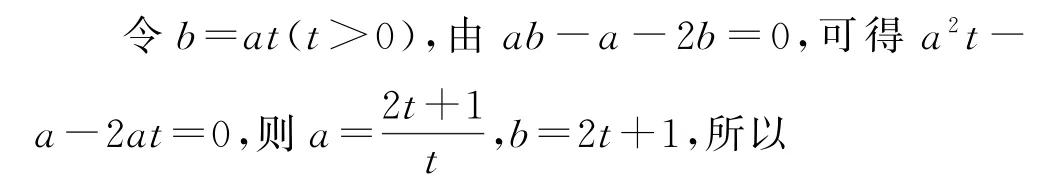
求二元代数式的最值或值域问题,不应仅限于基本不等式,有时可从方程判别式、导数等思路入手.由于此类题型结构一般短小精悍,解答灵活多变,变形思维要求较高,所以在平时的学习或复习过程中,学生要先运用已有知识及方法尝试性地解决问题,再在教师的引导下归纳总结,这样对问题的理解才能逐步深入,进而抓住问题本质,只有这样才能在考试中找到合理的解题途径,提高解题效率.同时平常多进行一题多解训练,有利于调动自己的学习积极性,培养发散性思维,有利于锻炼思维的灵活性,灵活地选择解题切入点.更重要的是解题后要做到一题多思、多变,对多种解法进行反思,提炼共性,区分个性,揭示不同解法之间的关联.善于总结试题规律,能做到一题多解、多思、多变,高考数学备考就会收获多多.

链接练习

链接练习参考答案

(完)