2022年清华大学强基计划测试数学第13题的解答与推广

吴 康

(华南师范大学)

题目(2022年清华大学强基计划测试数学第13题)已知ax＋by＝1,ax2＋by2＝2,ax3＋by3＝7,ax4＋by4＝18,则ax5＋by5＝_________.

据学生回忆,2020年清华大学强基计划测试数学试题共20道选择题,2021年情况类似.本题也是学生回忆版,真实情况待定.如果懂得广义二阶幂和式的递推性质,可在3分钟内解决.以下给出解答与推广.

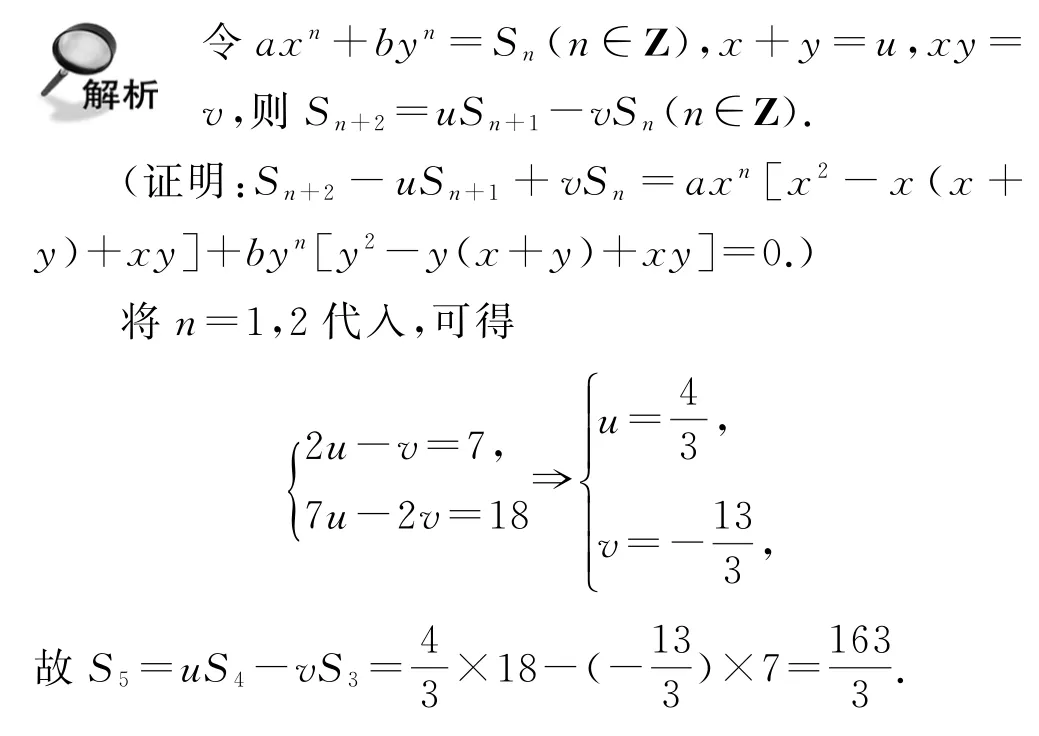
点评本题有多种推广方法,以下自编问题均为填空题,难度中等,计算量适中至稍大,可供类似考题参考.

点评从前两个方程消去S1,再将第三个方程代入,可得关于u的一元二次方程.本题是已知Sn(n＝0,2,3,4)的值,求S5,因所知Sn的下标n的值不连贯,少了n＝1,导致符合本题要求的解有2个.

将n＝0,1,2代入,可得关于u,v,S2的三元二次方程组

点评前两个方程消去S0,得u2＝uS2＋v,与后两个方程可消去S2,再消去v,化简可得(u－1)2(u2＋2u－9)＝0.本题是已知Sn(n＝－1,1,3,4)的值,求S0S2S5,因所知Sn的下标n的值有两处不连贯,少了n＝0,2,导致符合本题要求的解有3个.其实应认为本题有4个解,其中2个解相同,有1个解就是著名的斐波那契数列.

点评求解本题用到了广义三阶幂和式的递推性质.此类型可继续推广.

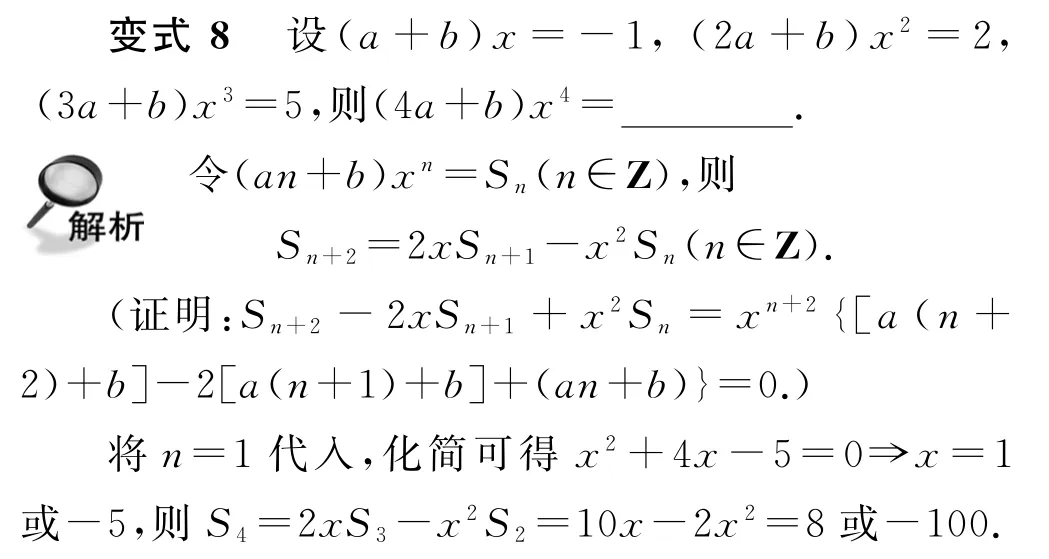
点评求解本题用到变系数广义幂和式的递推性质,也可直接求解题设方程,得(a,b,x)＝(3,－4,1)或(－,－5),稍繁.

变式9设(a＋b)x＋cy＝0,(2a＋b)x2＋cy2＝－1,(3a＋b)x3＋cy3＝2,(4a＋b)x4＋cy4＝18,(5a＋b)x5＋cy5＝70,(6a＋b)x6＋cy6＝214,则(7a＋b)x7＋cy7＝________.则S7＝uS6－vS5＋wS4＝5×214－8×70＋4×18＝582.

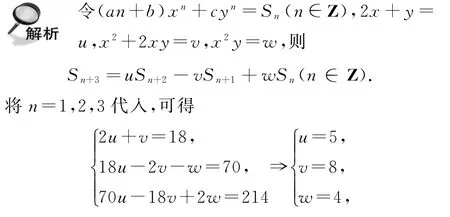
点评求解本题用到变系数广义幂和式的递推性质,若直接求解题设方程,将会相当烦琐.

在不超过4阶的情形,还有f(t)为(t－x)(t－1),(t－x)2(t－1),(t－x)4,(t－x)2(t－y)(t－1)和(t－x)(t－y)(t－z)(t－u)这几类的幂和式问题,留给对命制数学问题感兴趣的读者.以下问题针对三角函数的特殊形式命制,其背景仍为广义幂和式.

点评本题直接通过解方程求b和θ的值,则计算量较大.

等的数列{Sn},已知若干项求其他项的题目,留给感兴趣的读者.

(完)