磁偶极子源电磁场代数解与积分解的数值计算
2022-10-25洪德成王海军
洪德成,王海军
(吉林大学 物理学院,吉林 长春 130012)
随着计算机模拟技术的发展,在科学研究领域,计算物理学与理论物理学、实验物理学成为当代物理学发展的三驾马车.但在目前的大学物理教育体系中仍以理论物理为主,实验物理次之,计算物理再次之.理论物理和实验物理都已建立起成熟而完备的教学体系,而计算物理起步晚,发展缓慢,教学案例较为有限[1-3].
本文针对磁偶极子源,从麦克斯韦方程组出发,通过引入赫兹势推导无限大均匀介质中电磁场代数表达式和积分表达式,并给出相应的数值计算方法.代数解形式简单、参数关系明确,但不能处理含有边界的非均匀介质电磁场问题;积分解适用性较广,可进一步扩展到水平层状分层、圆柱状分层及球状分层介质中电磁场分布问题的求解[4-9].根据不同的边界类型(水平边界、圆柱边界、球形边界),积分解的具体表达形式也不同.
为简明起见,本文给出适用于水平分层介质的电磁场积分解.积分表达式为包含贝塞尔函数的高阶震荡无穷积分(也称Sommerfeld积分).采用三次样条拟合、高斯-勒让德数值积分[7]、以及两种算法相结合的方式分别求解Sommerfeld积分.
1 磁偶极子源的电场和磁场
1.1 场的代数解
无限小电流环可等价为磁偶极子源,设电流随时间变化为e-iωt,麦克斯韦方程组满足如下形式:

(1)

(2)
介质的本构关系:
B=μH+μMδ(r),D=εE,J=σE
(3)
其中μ、σ和ε分为介质磁导率、电导率和介电常量.M代表磁偶极子源强度.将式(3)代入式(1)、式(2)得

(4)

(5)
其中σ*=σ-iωε为复电导率.对式(5)取散度,并考虑到·(×A)=0,得

(6)
由此引入赫兹势π[8]:
E=iωμ×π
(7)
同时,令赫兹势π满足如下散度方程:

(8)
将式(7)代入式(5)得磁场表达式:
H=iωμσ*π+φ
(9)
将式(7)、式(8)代入式(4),得到如下赫兹势方程:

(10)

(11)
式(10)进一步展开为
(12)
可以看出,由于空间对称关系,每个分量满足形式相同的偏微分方程.这里我们只考虑z方向磁偶极子源Mz.即令Mx=My=0,则式(12)的解为[8]
(13)
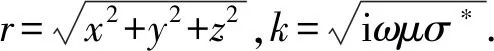
(14)
将式(13)代入式(7),得到电场分量表达式:
Ez=0
(15)
将式(13)和式(14)代入式(9),得到磁场分量表达式:
(16)
1.2 场的积分表达式
在圆柱坐标系(ρ,φ,z)中,有如下恒等式[8]:
(17)

(18)
进一步将式(18)代入式(8)得标势φ积分表达式:
(19)
将上面二式分别代入式(7)和式(9),并应用柱坐标系下偏微分算子得电场分量:
Eρ=0,
Ez=0
(20)
及磁场分量:
Hφ=0,
(21)
(22)
2 数值积分方法
式(20)和式(21)中的Sommerfeld积分可统一写为如下形式:
(23)
本文分别采用三次样条插值、高斯-勒让德积分及这2种方法结合的方式求解式(23)的数值积分.
2.1 三次样条拟合积分方法
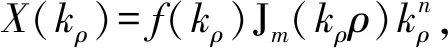
(24)
其中,多项式系数由下式给出:
(25)
式中hj=kρ,j+1-kρ,j为离散点间隔,参量Mj由下列矩阵求解:
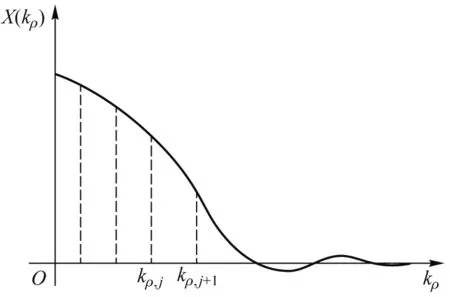
图1 被积函数随自变量变化关系

(26)
方程两侧矩阵元素分别为:
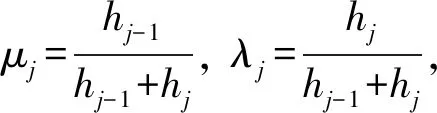
d1=d2,dN+1=dN
(27)
在数值计算中,通常将式(23)的无穷积分截断为有限积分.取kρ,N+1为积分上限,kρ,N+1以后对应的被积函数足够小,在满足积分精度要求下可以忽略不计.由式(25)—式(27)确定所有区间内的三次函数系数后,每一区间积分结果为
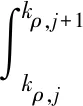
(28)
将所有区间积分结果相加即为式(23)的积分结果.
2.2 高斯-勒让德积分方法
高斯-勒让德积分是一种将积分运算转换为乘积运算的成熟数学积分方法,其运算规则如下:
(29)
其中,方程左侧g(t)是任意形式的被积函数,积分限为[-1,1];方程右侧为采样点对应函数值与加权系数的乘积的和,其中tl为自变量分布在[-1,1]区间的固定采样点,Wl为对应点的加权系数.
例如:当L=5时,有
tl=±0.906 179 845 9,Wl=0.236 926 885 1
tl=±0.538 469 310 1,Wl=0.478 628 670 5
tl=0,Wl=0.568 888 888 9
一般来讲,阶数L越大数值结果精度越高,但耗时也越多.
在求解式(23)积分时,首先将被积函数划分为若干区间,然后对每一区间积分上、下限做变量替换.令
(30)
则每一区间的积分变形为
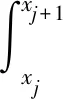
(31)
与式(29)对照,应用高斯-勒让德积分方法即可求出该区间的积分结果,然后将所有区间结果相加即为式(23)的积分结果.
2.3 三次样条拟合结合高斯-勒让德积分方法
三次样条拟合方法和高斯-勒让德积分方法都可以独立求解式(23)的数值积分问题,为增加对积分方法的深入理解与灵活应用,也可将两种方法结合起来.采用三次样条函数拟合式(23)中被积函数随自变量变化相对平滑的部分:
(32)
该区间内的函数积分可进一步表达为
(33)
式(33)右侧积分可采用上述的高斯-勒让德积分方法求出.
上述3种积分方法是严格完备的,理论上,计算结果也可以无限逼近真实值.但计算机编程中总会存在由多种因素引起的计算误差,其中被积分函数形态及采样点分布规则是常见的主要因素.对同一积分问题采用不同的积分方法,一方面可以相互验证数值积分结果的正确性,另一方面也可通过对计算精度和计算效率的评估优选出最适合该问题的最佳积分方法.
3 数值结果
本小节针对一个给定的物理模型,给出电磁场分量的数值计算结果.假定介质磁导率为真空磁导率μ=μ0=4π×10-7H/m;介电常量为真空介电常量ε=ε0=8.854×10-12F/m,电导率σ=0.1 S/m.磁偶极子强度Mz=1 A·m2,频率f=20 kHz.发射点位置(0,0,0),场点位置(0.5,0,1).表1给出了代数解与积分解对比结果.可以看出3种积分数值结果与代数解吻合,证明了理论方法的正确性.数值结果有效数字后几位的计算误差主要来自于对积分上下限的截断及积分区间分割的位置、数量多少等.
4 结论
本文从麦克斯韦方程出发推导了磁偶极子源在均匀介质中激发的电磁场代数解与积分解.并采用三次样条拟合方法、高斯-勒让德积分方法及它们的结合方式分别求解Sommerfeld数值积分.为学生提供了一个以电动力学为背景的计算物理教学案例.
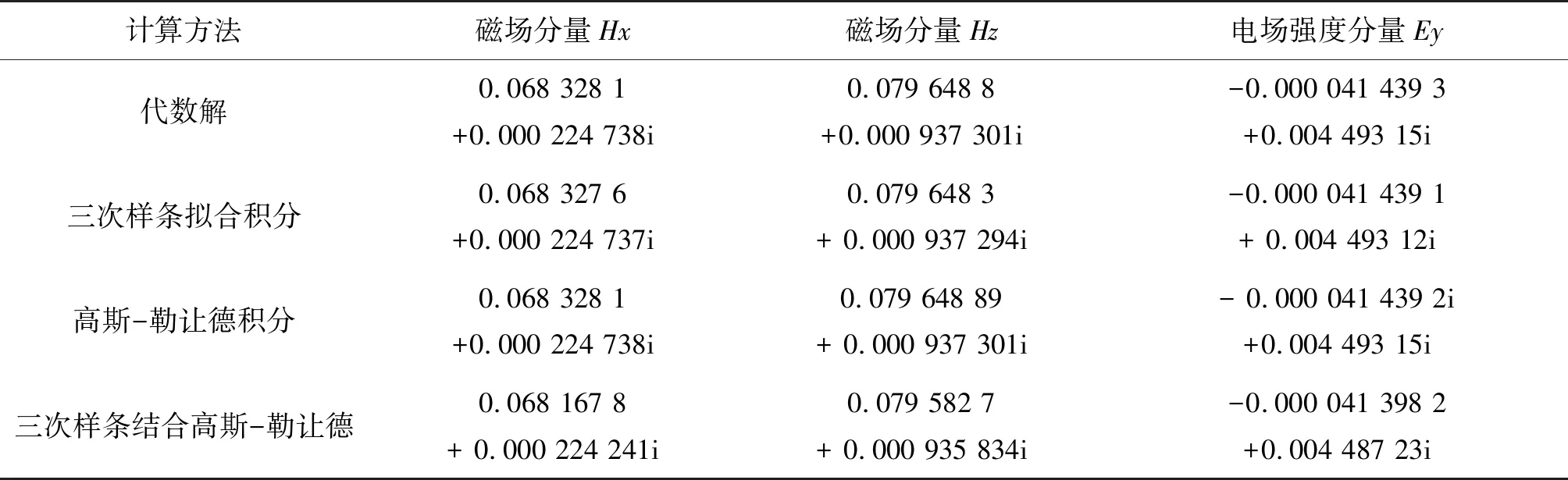
表1 电磁场代数解与积分解数值对比
