同极滚轮放置在铝箔上的运动状况的研究

王荣超，徐小雯，柳辛迪，董 琪

(成都信息工程大学 光电工程学院电子科学与技术系，四川 成都 610200)

2021年6月初，参加第五届西南地区大学生物理学术竞赛，从比赛题目：“不同直径的纽扣磁铁被连接到圆柱形电池的两端. 放置在铝箔上时，物体开始旋转，研究相关参数如何影响该运动. ”中受到启发. 利用紧贴在电池两端的两块相同极性的纽扣磁铁和电池组成的滚动装置，以下称为同极滚轮. 对放置在铝箔上的同极滚轮，在磁铁半径相同与不同时的运动情况进行了研究. 从Seán M. Stewart[1]等的研究中发现，电池两端磁铁半径相同的同极滚轮为从动轮，在运动过程中磁铁的极性保持不变. 电池提供的电流通过磁铁内侧面，其方向与磁场方向垂直，受到垂直于磁场与电流方向的安培力，并产生力矩，滚轮旋转，产生磁铁与桌面接触点的角速度方向相反的摩擦力，滚轮发生直线运动. 但后期的分析中未考虑到温度对磁铁剩磁的影响. 在Guala-Valverde[2]的观点中使用U形连接线连接磁铁两端，形成导电回路. 但U形连接线与磁铁端的接触并不紧密，在同极滚轮运动的过程中，电路连接可能出现断连的情况，导致滚轮受力消失，运动过程不稳定. 连接线同样受到磁场的作用，产生竖直向下的力，且与磁铁的接触点会产生摩擦力. 在前人研究的基础上，将以连接线完成电路连接的方式，替换为滚轮放置在铝箔上完成导电回路. 铝箔较铜等金属而言，具有较好的延展性的同时，比同样具有较好延展性的锡纸，有着更高的熔点(铝箔纸熔点660 ℃，锡纸熔点231.89 ℃)，且铝箔这类材料价格低廉. 并将温度对剩磁的影响考虑到滚轮的运动过程中.

1 简化动力学分析

1.1 磁铁电流流向

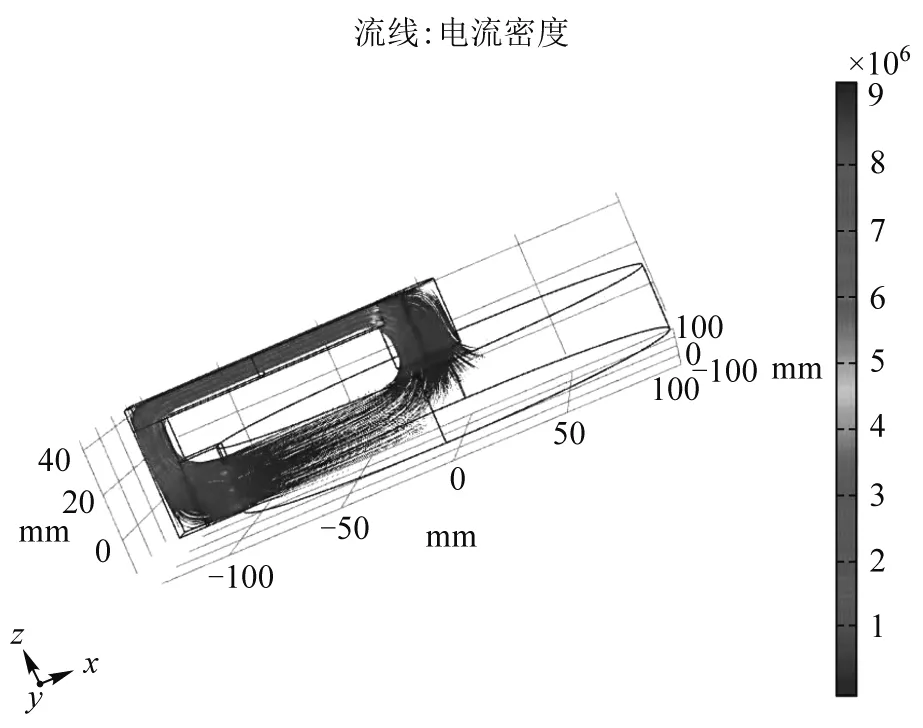
图1 电流密度在纽扣磁铁中的分布

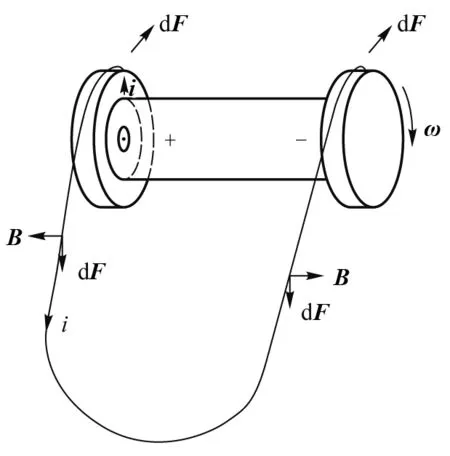
图2 U形同极滚轮系统分析图

1.2 磁铁剩磁受温度的影响

由石生磊等[3]对磁性材料的高温特性的研究发现，磁性材料随着温度的上升，分子的热运动变得强烈，导致金属点阵电子的热运动也变得强烈，破坏磁畴的有序排列，而当磁性材料的温度高于居里温度时，磁畴会被完全破坏，失去导磁能力.系统形成的回路中接入的电阻小，系统发热明显，短时间内磁铁的温度会迅速上升.孙曌续等[3]对永磁体升温时剩磁的研究得知，温度升高永磁体的剩磁都会下降，温度处于工作范围内时，其下降趋势近似为线性变化，剩磁随温度的变化满足

(1)

Br20为20 ℃时剩磁的密度；aBr为Br的可逆温度系数；L为Br的不可逆损失率；t为预计工作温度.

基于孙曌续等[4]和刘艳丽等[5]的研究选磁铁从0 ℃到200 ℃时，取Br的可逆温度系数为-0.03%，不可逆损失率为53.6%，Br20为1.16 T.做出剩磁与温度的关系图，如图 3所示.在工作温度内，永磁体剩磁随温度的变化量较小.本文选用的电池电压仅为1.5 V，滚轮运动过程中的温度不会超过工作温度，由此近似认为同极滚轮运动过程中磁场强度B=Br20.

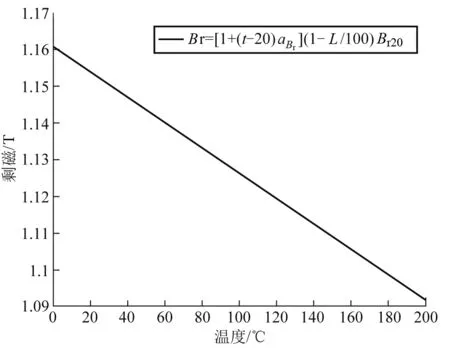
图3 磁铁剩磁随温度变化图

1.3 半径相同滚轮的运动分析1.3.1 回路电流的变化

电池两侧的磁铁半径为r1，两端纽扣磁铁的固定电阻为R1，铝箔电阻相对磁铁固定电阻相比可忽略不计，电池的输出电压为V1，虽滚轮运动时会产生反电动势V2且随着角速度ω的变化而变化，但反电动势的产生只对电流的大小有阻碍作用，并不对电流的方向产生影响.在磁场强度为B的磁场作用下，对每一个径向单位dL上的合力为

dF=idL×B

(2)

对一侧磁铁受力进行积分其合力为

F=i∮dL×B

(3)

由法拉第定律得，两侧磁铁均会产生反电动势:

(4)

(5)

反电动势的存在，系统电压随着旋转速度增大而减小，最终达到0 V，式(4)中的电流值接近零.

1.3.2 同极滚轮位移与时间的关系

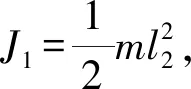
(6)

以带有单位基向量的笛卡儿坐标系〈ex1,ey1,ez1〉来表示系统的受力方向，如图4所示.取dL=dyey1，r3=yey1，B=Bez1，r3为坐标原点指向当前元素的位置向量.

图4 笛卡儿坐标系下相同半径系统分析图

电池一端的磁铁受到的安培力为

F=i∮dL×Bez1=iBl2ex1

(7)

合力矩为

(8)

同极滚轮为不打滑的从动轮，在运动过程中，磁铁与铝箔接触面产生的滚动摩擦力可以忽略不计.滚轮受到与运动方向相同的静摩擦力f，在笛卡儿坐标系中表示为f=fex1.

根据牛顿第二定律，系统的总合力为

∑F2=2F-2f=2iBl2ex1+2fex1=(M+2m)a

(9)

这里的a为系统的加速度.系统的总力矩为

(10)

这里的α为滚轮的角加速度.

同极滚轮在转动过程中与铝箔之间无滑动滚动，因此其转动时的加速度与系统加速度相等，因此系统的加速度与滚轮的角加速度满足关系式：

a=l2α

(11)

将式(11)代回式(15)可计算得a：

(12)

从式(9)中可以得到a的另一种表达方式:

(13)

结合式(12)、(13)定义一个新的值:

(14)

结合式(4), 得

(15)

滚轮的线速度v1与系统运动时的速度相等，满足圆周运动的关系式:v1=l2ω

(16)

对式(15)进行分离积分，系统质心满足从静止开始到保持稳定速度时线速度vT与时间t的关系:

(17)

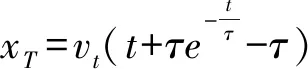
(18)

1.4 系统能量分析

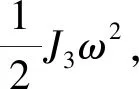
(19)

由焦耳定律可得，滚轮运动时产生的热量为

Qt=I2R1t

(20)

我们定义输出的功率为WO，力f为静摩擦力并不做功，因此整个系统的能量关系为

(21)

1.5 半径不同时滚轮的运动分析1.5.1 滚轮受力分析

半径小的磁铁A其半径为rA，质量为mA.半径大的磁铁B其半径为rB，质量为mB.磁铁A的运动半径为RA，磁铁B的运动半径为RB.磁铁A、B与电池仍围绕同一个转轴旋转.回路以串联连接，流过两磁铁为电流ix，由式(5)可得

(22)

由前面对磁铁安培力的分析，我们可以得知磁铁A、B受到的安培力分别为

FA=ixBrAex2

(23)

FB=ixBrBex2

(24)

1.5.2 磁铁半径与磁铁运动半径的关系

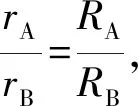
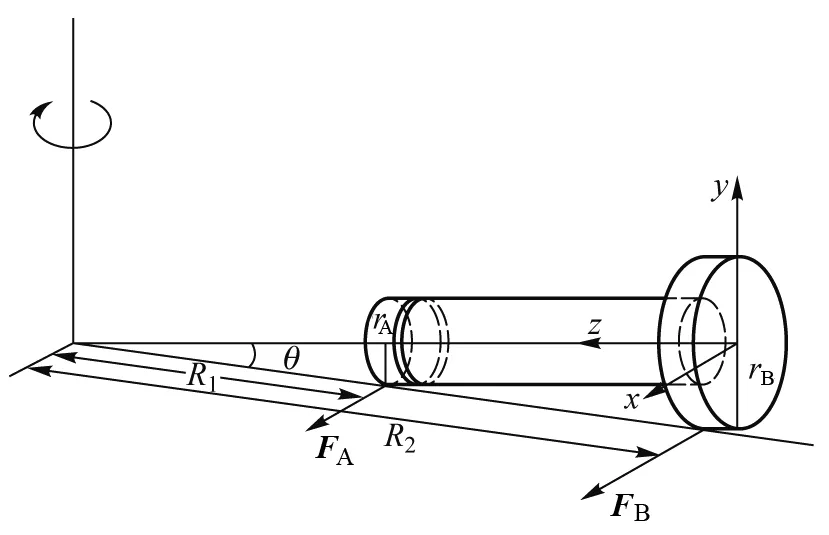
图5 不同半径下滚轮系统分析图

2 实验与仿真

2.1 半径相同时位移与时间关系2.1.1 实验装置

实验选取半径为7.10 mm，质量为 23.8 g的1.5 V碱性电池，宽度为30 cm的铝箔纸，以及半径为10 mm，磁场强度约为1 T，质量为23.04 g，中心到边缘的阻抗约为0.3R的纽扣磁铁，如图6所示.

图6 实验装置实物图

2.1.2 理论计算与实验仿真

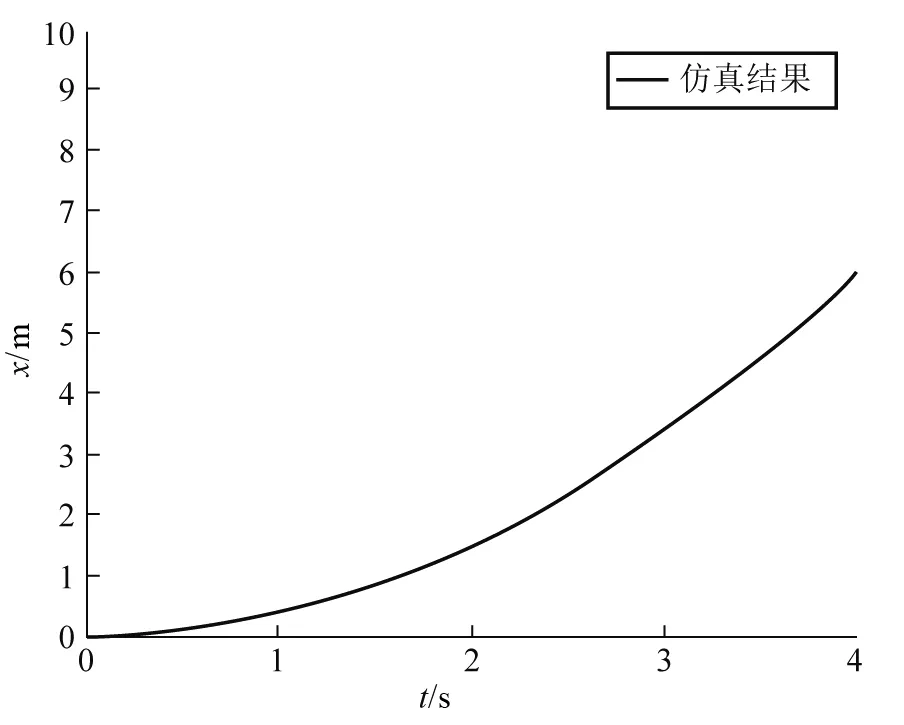
图7 位移与时间关系曲线

2.1.3 实验值与理论值误差分析

实验中为保证电池的电量充足，选取时间为3 s时滚轮运动的位移量.经实验测得滚轮在第3 s时的位移量为2.94 m，与理论值3.4 m相差0.46 m.实验与理论值的误差是由于铝箔纸的可塑性比较强，铺在水平地面，难免会造成微小的褶皱，对滚轮的运动产生阻碍.两端磁铁与电池的旋转轴在运动过程中会出现微量位移，可能并非同一旋转轴.

2.2 半径不同时磁铁半径与磁铁运动半径的关系2.2.1 实验测量

表1 磁铁半径与磁铁运动半径的关系

2.2.2 误差分析

由表1可知，在磁铁半径为5 mm和7.5 mm时，相对百分比有13.04%，在两端磁铁的半径为5 mm和15 mm时，相对百分比有9.31%.误差产生的原因也与0～3 s内的位移随时间变化相同.

3 结束语

受到比赛的启发，对前人研究同极滚轮的装置进行了修改以及温度对剩磁影响的考虑.运用仿真软件仿真出磁铁通过电时电流径直由一端流向另一端，结合前人研究绘制出磁铁剩磁与温度的关系图，运用简化动力学分析出滚轮的运动过程，得到了相同半径时位移与时间的关系，不同半径时，磁铁半径与内外圆周运动的半径的关系.运用仿真与实验结合的方式，分析理论值与实际值产生误差的原因.未来研究方向可为滚轮在运动过程中铝箔纸的褶皱问题，以及存在电流密度叠加情况下的应用[6].最后，感谢我的老师以及与一起比赛的队友们，对完成这篇论文，他们给了我很大的鼓励.