一类具有非瞬时脉冲发展方程适度解的存在性

吴 博, 范虹霞

(兰州交通大学数理学院, 兰州 730070)

脉冲微分方程是微分方程理论中一个重要分支, 近几年来, 瞬时脉冲微分方程不仅在物理、化学、工程学和生物学等方面已有很多成果[1-3], 而且在航天技术、信息科学等科技领域也发挥了重要的作用[4-5]．2016年, Diallo等[6]利用预解算子和Sadovskii不动点定理, 讨论了具有非局部条件和瞬时脉冲的积-微分方程

适度解的存在性．由于药物进入血液的过程及随后身体对药物的吸收过程都是渐进而持续的, 这一过程无法用经典的瞬时脉冲微分方程解释[7], O’Regan等[8]在研究药物动力学的背景下, 首次提出非瞬时脉冲微分方程．此后, 非瞬时脉冲微分方程引起了国内外学者的广泛关注[9-11]． 2016年, 陈鹏玉等[12]在解半群是非紧的情形下, 利用非紧性测度研究了非瞬时脉冲微分发展方程

适度解的存在性．

受上述文献的启发, 本文考虑具有非瞬时脉冲的一阶积-微分非自治方程

(1)

1 预备知识

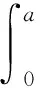
下面介绍积-微分非自治方程预解算子的定义与一些性质, 为此考虑方程(1)相应的线性方程

(2)

其中A(t)和B(t,s)是X上的闭线性算子．

设Y是由A(t)的定义域D(A)构成的Banach空间, 具有图像范数‖y‖Y=‖Ay‖+‖y‖．B(Y,X)表示Y→X中全体有界线性算子构成的空间．

i) 映射(t,s)→R(t,s)是强连续的,R(s,s)=I,并存在常数β和M≥1, 使得对∀(t,s)∈T, 有‖R(t,s)‖≤Meβ(t-s);

ii) 对∀(t,s)∈T,R(t,s)Y⊂Y, 且R(t,s)在Y上关于t和s是强连续的;

iii) 对∀(t,s)∈T, 如果x∈D(A), 那么R(t,s)x关于t和s是强连续可微的, 且

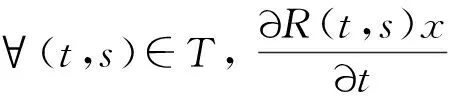
为了确保方程(2)的预解算子存在, 对A(t)和B(·,·)提出以下假设:

(H1)A(t)在Banach空间X中生成一个强连续发展半群．

(H2) 假设Y是D(A)构成的Banach空间．令A(t)和B(t,s)是闭算子, 对∀t∈J,A(t):Y→X是有界算子集, 对∀(t,s)∈T,B(t,s):Y→B(Y,X)是有界算子集． 进一步,A(t)和B(t,s)是连续的．

引理1[13]若条件(H1)和(H2)成立, 则方程(2)存在唯一的预解算子．

用α(·)表示X中有界集的Kuratowski非紧性测度;αC(·),αP(·)分别表示C(J,X),P(J,X)中有界集的Kuratowski非紧性测度．下面给出有关Kuratowski非紧性测度的一些性质．

引理2[14]设X,Y是实Banach空间,S,U是X中的有界集,则有下列性质:

i)S相对紧⟺α(S)=0;

iii) 若S⊆U, 则α(S)≤α(U);

iv)α(S+U)≤α(S)+α(U), 其中S+U={x+y:x∈S,y∈U};

v)α(S∪U)≤max{α(S),α(U)};

vi)α(λS)≤|λ|α(S), 其中λ∈R;

vii) 若映射Q:D(Q)⊆X→Y是Lipschitz连续的, 且Lipschitz常数为k, 则对任意的有界集S⊂D(Q), 有α(Q(S))≤kα(S)．

引理3[15]设X是Banach空间,D⊂X有界, 则存在可数集D0⊂D, 使得α(D)≤2α(D0)．

引理4[15]设X是Banach空间,D={un}⊂P([b1,b2],X)是有界可数集, -∞

引理5[15]设X是Banach空间,D⊂C([b1,b2],X)是有界且等度连续集, 则α(D(t))在[b1,b2]上连续, 并且αC(D)=maxt∈[b1,b2]α(D(t))．

接下来给出k-集压缩映射的定义和Darbo不动点定理．

定义2[16]设X是Banach空间,S⊂X是非空子集, 若Q:S→X连续有界, 存在常数k∈[0,1), 对任意有界集Ω⊂S, 满足α(Q(Ω))≤kα(Ω), 则称Q是S上的k-集压缩映射．

定理1[16](Darbo不动点定理) 设X是Banach空间,Ω⊂X为有界凸闭集, 若Q:Ω→Ω为k-集压缩映射, 则Q在Ω上至少有一个不动点．

最后, 结合文献[14], 给出方程(1)适度解的定义．

定义3若函数u∈P(J,X)满足积分方程

则称u是方程(1)的适度解．

令r>0为有限常数, 并记Ωr={u∈P(J,X): ‖u‖P≤r,t∈J}．

2 主要结果

为了得到方程(1)适度解的存在性, 给出下列假设条件:

(H3) 预解算子R(t,s)是一致连续的, 且存在常数Ra≥1,使得sup(t,s)∈T‖R(t,s)‖≤Ra．

(H4) 函数f:J×X×X→X满足:

i)f(t,·,·):X×X→X, 对t∈J几乎处处连续, 且f(·,x,y):J→X对x,y∈X×X强可测;

ii) 存在函数η∈L1(J;R+), 使得对几乎处处t∈J,∀x,y∈X, 有

‖f(t,x,y)‖≤η(t)(‖x‖+‖y‖);

iii) 存在函数l∈L1(J;R+), 使得对任意的有界集A,B⊂X且对几乎处处t∈J,有

α(f(t,A,B))≤l(t)(α(A)+α(B))．

(H5) 函数h:T×X→X满足:

i)h(t,s,·):X→X,对(t,s)∈T几乎处处连续, 且h(·,·,x):T→X对x∈X强可测;

ii) 存在函数m∈L1(T;R+),有‖h(t,s,x)‖≤m(t,s)‖x‖;

iii) 存在函数ζ1,ζ2∈L1(J;R+), 使得对任意的有界集D⊂X, 且对几乎处处(t,s)∈T, 有α(h(t,s,D))≤ζ1(t)ζ2(s)α(D)．

(H6) 函数γk:[tk,sk]×X→X连续, 并且存在常数Kγk>0,k=1,2,…,m, 对任意的u,v∈X有‖γk(t,u)-γk(t,v)‖≤Kγk‖u-v‖,∀t∈(tk,sk]．方便起见,记

(3)

(4)

(5)

定理2若条件(H1)～(H6)成立, 且

Ramax{K+Ψ+m*Ψ,K+4L}<1,

(6)

则方程(1)在区间J上至少存在一个适度解．

证明 定义算子F:P(J,X)→P(J,X)为

(Fu)(t)=(F1u)(t)+(F2u)(t),

(7)

其中

(8)

(9)

为了使用Darbo不动点定理, 将分6步证明算子F至少有一个不动点．

第1步证明Fu∈P(J,X), 对∀u∈P(J,X)．

情形2t∈(tk,sk], 由式(7)～(9)及条件(H6), 非瞬时脉冲函数γk(t,u(t))(k=1,2,…m)是连续的, 故对∀u∈P(J,X),Fu∈C((tk,sk],X),k=1,2,…m．

综上所述, 对∀u∈P(J,X),Fu∈P(J,X)．

第2步证明存在常数r>0, 使得F(Ωr)⊂Ωr． 如若不然, 对任意的r>0, 存在ur∈Ωr,tr∈J, 使得‖F(ur)(tr)‖>r．

情形1tr∈[0,t1], 由式(7)～(9), 条件(H3)～(H5)及式(4)～(5)有

(10)

情形2tr∈(tk,sk],k=1,2,…m, 由式(7)～(9), 条件(H6)及式(3)有

‖(Fur)(tr)‖≤Kγk‖ur(tr)‖+‖γk(tr,θ)‖≤Kγkr+N≤Kr+N,

(11)

其中

N=maxk=1,2,…,msupt∈J‖γk(t,θ)‖．

(12)

情形3tr∈(sk,tk+1],k=1,2,…,m, 由式(7)～(9), 条件(H3)～(H6)及式(3)～(5)和(12)有

(13)

由式(10),(11),(13), 并结合r<‖F(ur)(tr)‖, 有r<‖F(ur)(tr)‖≤Ra[‖u0‖+(K+Ψ+m*Ψ)r+N]．两边同时除以r, 并令r→+∞, 得1≤Ra(K+Ψ+m*Ψ)．这与式(6)矛盾．

第3步证明算子F1:Ωr→ΩrLipschitz连续．

情形1t∈(tk,sk],k=1,2,…m,∀u,v∈Ωr, 由式(8)及条件(H6)有

‖F1u(t)-F1v(t)‖≤Krk‖u(t)-v(t)‖≤Krk‖u-v‖P．

(14)

情形2t∈(sk,tk+1],∀u,v∈Ωr, 由式(8)及条件(H3)和(H6)有

‖F1u(t)-F1v(t)‖≤RaKγk‖u(sk)-v(sk)‖≤RaKγk‖u-v‖P．

(15)

由式(3),(14),(15), 得‖F1u-F1v‖P≤RaK‖u-v‖P．

第4步证明算子F2在Ωr上连续．设{un}⊂Ωr是一个序列, 且limn→+∞un=u,u∈Ωr,由函数f和h的连续性可知, 对∀s∈J, 有

(16)

由式(9),(16)及条件(H3),有

当n→+∞时, 由Lebesgue控制收敛定理, 得‖(F2un)-(F2u)‖P→0, 故F2在Ωr上连续．

综上所述, ‖(F2u)(t″)-(F2u)(t′)‖→0,故F2:Ωr→Ωr等度连续．

第6步证明F:Ωr→Ωr是k集压缩映射．对任意的有界集D⊂Ωr, 由引理3可知,存在一个可数集D0={un}⊂D,使

αP(F2(D))≤2αP(F2(D0))．

(17)

因F2(D0)⊂F2(Ωr)有界且等度连续,故由引理5可知

αP(F2(D0))=maxt∈[sk,tk+1],k=0,1,…,mα(F2(D0)(t))．

(18)

α(F2(D0)(t))≤2RaLαP(D),

(19)

故由式(17)～(19),αP(F2(D))≤4RaLαP(D)．由引理2中(vii)并结合第3步可知,对任意有界集D⊂Ωr, 有αP(F1(D))≤RaKαP(D), 故αP(F(D))≤αP(F1(D))+αP(F2(D))≤Ra(K+4L)αP(D)．结合式(6),由定义2可知,F:Ωr→Ωr是k-集压缩映射．

因此, 由Darbo不动点定理可得算子F在Ωr上至少有一个不动点, 即方程(1)在区间J上至少有一个适度解．