方程与不等式思想在“数与代数”问题中的应用——以2021年中考题为例

周泽军

(湖北省武汉市光谷实验中学,430223)

本文从概念、性质、图形或图象、实际应用四个方面探究方程与不等式思想在中考中的应用.

一、由概念产生方程与不等式

例1(2021年聊城中考题)关于x的方程x2+4kx+2k2=4的一个解是-2,则k的值为( )

(A)2或4 (B)0或4

(C)-2或0 (D)-2或2

解析此题考查了方程的解的概念.

把x=-2代入方程x2+4kx+2k2=4,得4-8k+2k2=4,解得k1=0,k2=4.故选B.

解析此题考查了二元一次方程(组)解的概念.

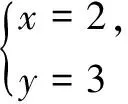
解析此题考查了解分式方程和解一元一次不等式.

将原分式方程去分母,得3x=-m+2(x-1),去括号、移项、合并同类项,得x=-m-2.由方程的解为正数,可得-m-2>0且-m-2≠1，解得m<-2且m≠-3.

评析本题的解题思路分为三步:一是求解关于x的分式方程,二是由题意得到关于m的不等式并解之,三是注意隐含条件(分式的分母不为零)对参数取值的限制.

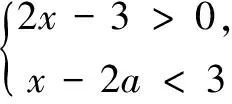
解析此题考查了解一元一次不等式组.

由题意，可得3<2a+3≤4,

评析对于含字母系数的不等式(组),先把其中的字母看作已知数,求出其解集(即用含字母的代数式表示解集),再依题对解集的具体限制,得到新的方程(组)或不等式(组),最后由新的方程(组)或不等式(组)解决问题.

二、由“性质”产生方程与不等式

(A)8 (B)6或8

(C)7 (D)7或8

解析此题考查等腰三角形的性质、三角形的三边关系、二元一次方程组等知识点,以及分类讨论思想.

由非负性,得到方程组

∴等腰三角形的周长为7或8,故选D.

例6(2021年广元中考题改编)将二次函数y=-x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图1所示.

(1)过点(4,0)的直线与新函数的图象只有1个公共点时,则直线的解析式是______.

(3)当直线y=x+b与新函数的图象恰有4个公共点时,则b的取值范围是______.

解析易得抛物线y=-x2+2x+3与x轴的交点为A(-1,0),B(3,0),翻折部分的抛物线解析式为y=(x-1)2-4(-1≤x≤3).

(1)分两种情况讨论:

当直线平行于y轴时,x=4.

(2)分三种情况讨论:

当直线与x轴平行且过(1,-4)时满足条件,此时y=-4.

根据题意,可设满足条件的直线解析式为y=x+b.

当直线y=x+b过点B(3,0)时,直线与新函数图象恰好有三个公共点.

此时,3+b=0,解得b=-3.

评析例6是利用一元二次方程根的判别式的性质解决问题.

三、由图形或图象产生方程与不等式

例7(2021年日照中考题)如图3,在矩形ABCD中,AB=8cm,AD=12cm,点P从点B出发,以2cm/s的速度沿BC边向点C运动,到达点C停止.同时,点Q从点C出发,以vcm/s的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v为______时,∆ABP与∆PCQ全等.

例8(2021年遂宁中考题)已知二次函数y=ax2+bx+c(a≠0)的图象如图4所示,有下列5个结论:①abc>0;②b2<4ac;③ 2c<3b;④a+2b>m(am+b)(m≠1);⑤ 若方程|ax2+bx+c|=1有四个根,则这四个根的和为2.其中正确的结论有( )

(A)2个 (B)3个 (C)4个 (D)5个

评析从知识的融合处设置问题,既可以考查学生思维的深度与广度,还可以有效地考查学生运用数学知识和思想方法解决问题的素养与能力.如,例7是方程思想在几何中的应用,例8是方程思想在函数中的应用.其中二次函数的图象与系数关系类问题主要考查图象的形状、大小、位置,函数解析式中系数变化与图象大小、图象位置的关系,函数的增减性、最值、图象对称性、函数值的大小比较等.

四、实际应用中产生的方程与不等式

例9“十一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.

根据图6提供的信息,解答下列问题:

(1)设租车时间为x小时,租用甲公司的车每日所需费用为y1元,租用乙公司的车每日所需费用为y2元,分别求出y1,y2关于x的函数表达式;

(2)当租车时间为多少小时时,两种方案所需费用相同;

(3)根据(2)的计算结果,结合图象,请你帮助小明分析选择怎样的出游方案更合算.

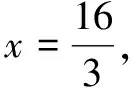
例10(2021年台湾中考题)碳足迹标签是一种碳排放量的标示方式,让大众了解某一产品或服务所产生的碳排放量多寡,如图7所示.碳足迹标签的数据标示有其规定,以碳排放量大于20公克且不超过40公克为例,此范围内的碳足迹数据标示只有20,22,24,…,38,40公克等11个偶数;碳足迹数据标示决定于碳排放量与这11个偶数之中的哪一个差距最小,两者对应标示的范例见表1.

表1

请根据上述资讯,回答下列问题,并详细解释或完整写出你的解题过程.

(1)若有一个产品的碳足迹数据标示为38公克,则它可能的碳排放量之最小值与最大值分别为多少公克?

(2)承(1),当此产品的碳排放量减少为原本的90%时,请求出此产品碳足迹数据标示的所有可能情形.

解析此题是一道开放性题,考查了不等式的相关知识.将现实生活中的情境与数学思想联系起来,需要理解题目所给的信息,并分析出各个数量之间的关系.第(1)问根据题干中关键语句“碳足迹数据标示决定于碳排放量与这11个偶数之中的哪一个差距最小”,可得碳排放量之最小值与最大值分别为37.0公克和39.0公克.第(2)问由第(1)问的最大值和最小值乘以90%,分别得到33.3公克和35.1公克,进而求出此产品碳足迹数据标示的所有可能情形为:34,36.

评析上述试题均是以实际问题为情境,注重培养与渗透学生的生活情境数学化能力.解答此类问题的关键是仔细分析题目的文字信息,从问题情境中抽象出数学问题,并建立数学模型.