一道袋鼠题

单 墫

(南京师范大学数学科学学院,210023)

香港小学高年级袋鼠竞赛第24题(倒数第二题，俗称压轴题)颇为有趣.原题如下：

在袋鼠小学，每位学生或者加入艺术俱乐部，或者加入体育俱乐部，或者两个俱乐部都参加.艺术俱乐部的学生中60%是男生，而体育俱乐部的学生中75%是男生.问袋鼠小学的全体学生中男生所占的百分比最小是多少？

(A)50% (B)57.5% (C)60%

笔者再增加一问：条件同上，男生所占的百分比最大是多少？

虽是小学生的赛题，大学师生未必能做啊！不信，你试试！

感觉男生人数应多于女生，至少不少于女生，即在全体学生中，男生所占百分比p≥50%.

不过这只是一个猜想，需要证明.选择支(A)——(E)以50%为最小，其实改其中之一为小于50%的数更好.

现在要做两件事：

(1)证明p≥50%;

(2)举例说明(1)中等号能够成立.如果举不出等号成立的实例，那么(1)或许要改为p≥57.5%或其他更大的值.

或许先做(2)更好.

设仅参加艺术俱乐部的男生为x人，仅参加体育俱乐部的男生为z人，同时参加两个俱乐部的男生为y人.相应地，女生人数为u,w,v,则有

①

②

显然将v中的1人去掉，而u，w各增加1人，则上述两个比值不变.因此，可设v=0.

同样，将x中1人，z中1人去掉，而y增加1人，上述比值也不变.因此，可设x或z为0.

为举例简单起见，不妨设x=z=0.

这时①、②即

③

y=3w.

④

而x+y+z=u+v+w,

即男生人数为总人数的50%.

现在证明(1)：

x,y,z,u,v,w意义同前，仍有

①′

y+z=3(v+w).

②′

若u≤2(v+w),则

y+z≥v+w+u.

⑤

若u>2(v+w),则

⑥

总之，x+y+z≥u+v+w,

所以x+y+z至少为总人数的50%.

以下再考虑男生所占百分比最大为多少？

与上面类似，举例可举y=0,u=w=0,则

z=3v.

取v=50,则x=75,z=150.

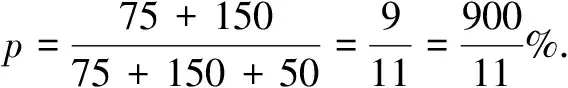
事实上，由①′,②′,得

2x+2y+2z≤2x+4y+2z

=3(u+v)+6(v+w)

=3u+9v+6w≤9(u+v+w).

上面的证法亦即

最小同样可求.