反比例函数中的面积模型及其应用
2022-10-25李晓侠
李晓侠
(山东省枣庄市台儿庄区马兰屯镇第二中学,277400)
在每年各地中考数学试卷中,与反比例函数有关的形态各异的图形面积问题时有出现.这类问题既考查反比例函数系数的几何意义,又充分体现数形结合的思想方法,我们只要熟练掌握了几种常见模型,就可得以快速解决.
一、一点一垂线模型
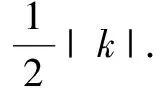
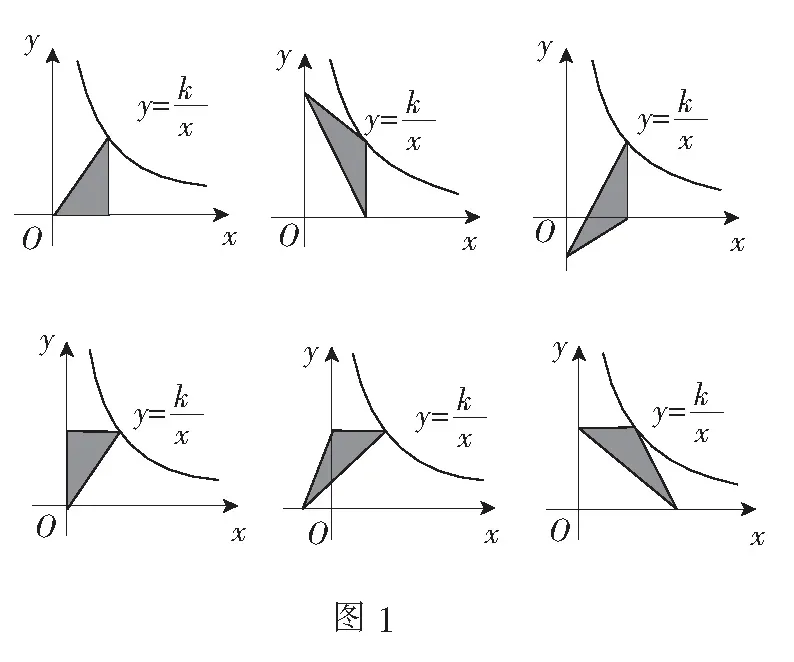
分析由∆OAB的面积为6,AB=3BC,可求出∆OBC的面积为2,进而求出∆OAC的面积为8,再根据反比例函数系数k的几何意义可求出k1,k2,进而得出答案.

∴S∆BOC=2,S∆AOC=2+6=8.
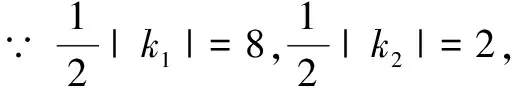
且k1<0,k2<0,
∴k1=-16,k2=-4,
∴k1+k2=-16-4=-20.


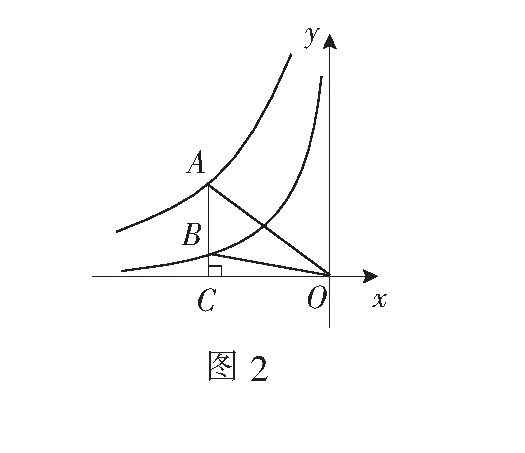
分析由∆OAC的面积以及∆PAB的面积,可求出∆OBC的面积,再根据反比例函数系数k的几何意义可求出k的值.
解如图3,连结OA,OB.
∵AC∥y轴,∴S∆AOB=S∆APB=2.


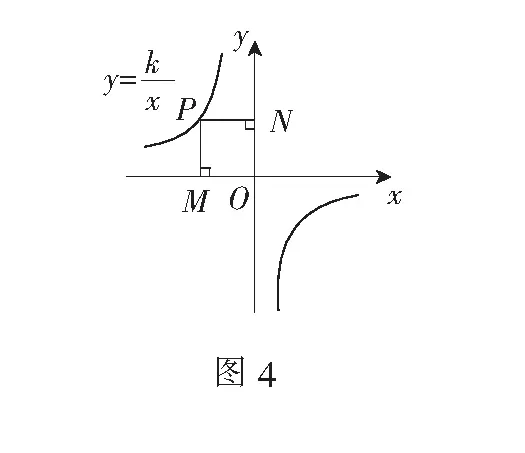
二、一点两垂线模型
结论如图4,反比例函数图象上一点与坐标轴的两条垂线所围成的矩形面积等于|k|.
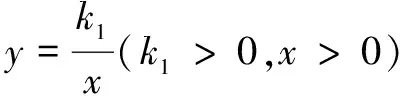
(A)① ② (B)① ③
(C)② ③ (D)①

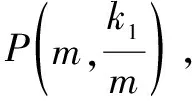
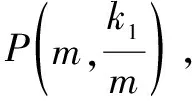

∴CD∥AB,故① 正确.
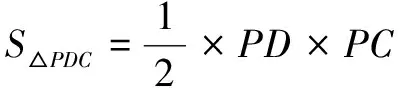
S∆OCD=S矩形OAPB-S∆OBD-S∆OCA-S∆DPC
∴③ 正确,② 错误.
故选B.
三、两点一垂线模型
结论如图6(1)(2),S∆ABM=|k|;





(1)求k的值;
(2)当点P的横坐标为-1时,求∆POQ的面积.

分析(1)过点P作PE垂直于x轴,垂足为E,只要求得∆PEO的面积,即可求得k的值.
(2)先求出直线PB的解析式,再求得Q点的坐标,最后由S∆POQ=S∆POB+S∆QOB即可求解.
解(1)如图7,过点P作PE垂直于x轴,垂足为E,则PE∥BO,∴∆ABO∽∆APE.
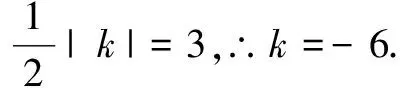
∴BO=4,B(0,4).
由P(-1,6),B(0,4),可得yBP=-2x+4.
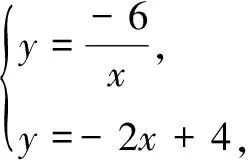
解得x1=3,x2=-1,∴Q(3,-2).
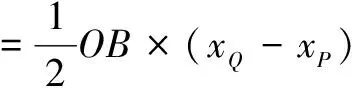
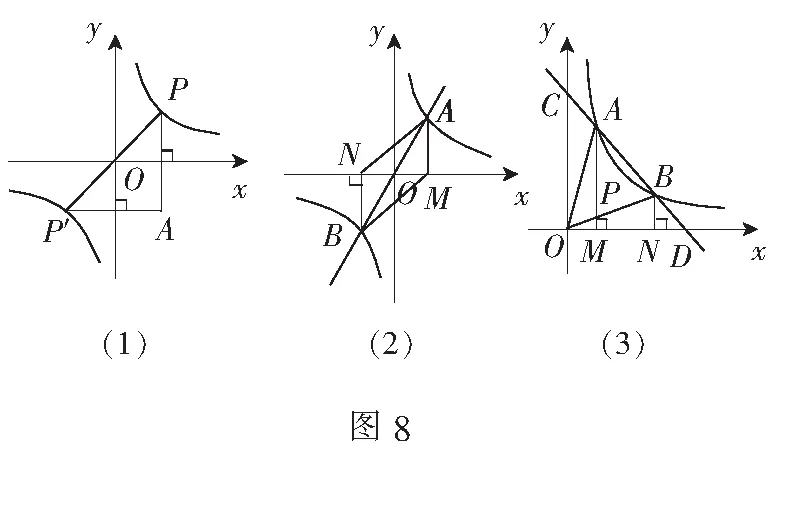
四、两点两垂线模型
结论如图8(1),S∆APP′=2|k|;
如图8(2),S=2|k|;
如图8(3),S∆OAB=S梯形AMNB.
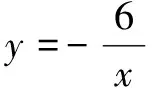
解析由模型(2),可得
点评本题作为一道填空题,用模型解答更为方便、快捷.


分析过点C作x轴的垂线,则由模型(3),可得S∆COD=S梯形ADCE,进而求得k的值.

如图10,作CE⊥x轴于点E,则由面积模型,可得S∆COD=S梯形ADCE,
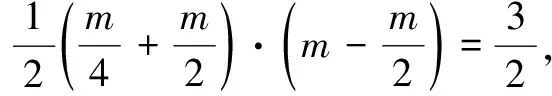

点评本题考查了反比例函数图象上点的坐标特征和反比例函数系数k的几何意义,其中根据面积模型得到关于m的方程是解题的关键.
