理解数学本质，推动智慧发展——以中考一轮复习课“列代数式及其应用”为例

葛东莲（河北省石家庄外国语学校）

进入九年级中考备考，很多数学教师常有“感觉复习不复习，结果差不多”“复习课难上，总复习课更难上”等困惑。带着对这些问题的思考，笔者进行了一轮复习课“列代数式及其应用”的教学探索。下面以这节课为例展现笔者的思考。

一、内容与学情分析

教学内容分析：借助现实情境列代数式，了解代数式的价值；体验从具体情境中抽象出数学符号的过程，探索具体问题中的数量关系和变化规律，掌握用代数式、方程、不等式、函数进行表述的方法；代数式上承用字母表示数，下启方程、不等式、函数的应用；代数式的性质就是代数学研究的主要内容。

学生学情分析：在此之前，学生已经对初中数学全部课程进行了学习，已经充分了解了初中数学的内容特点。本节课是一轮复习，需要站在学科整体的高度，引导学生重新认识数学知识的整体架构、发展脉络，理解代数式在研究数学、借助数学解决实际问题时的重要作用，以代数的眼光、思维观察问题，分析解决问题。

二、目标与重难点

教学目标：1.能分析具体问题中的简单数量关系，并用代数式表示量及量之间的关系，感悟数学抽象的一般过程。2.根据需要，能对所列代数式进行运算、推理，进而解决问题。3.理解代数式作为方程、不等式、函数的“重要组成部分”，能借助代数式构造相关数学模型，解决问题。

教学重点：1.分析具体问题中的简单数量关系，并用代数式进行表示。2.对所列代数式进行运算、推理，解决问题。

教学难点：理解代数式的价值——研究数量之间一般关系和规律。

三、教学实施过程

环节一：通过解决问题，回顾知识本源

教师提问：通过解决下列问题，你认为如何借助代数式解决问题？

某建筑公司承包了A、B两工地，现要从甲、乙两仓库向A、B两工地运送水泥．已知甲仓库可运出100吨水泥，乙仓库可运出80吨水泥，A工地需70吨水泥，B工地需110吨水泥．两仓库到A、B两工地的路程和每吨每千米的运费如下表。

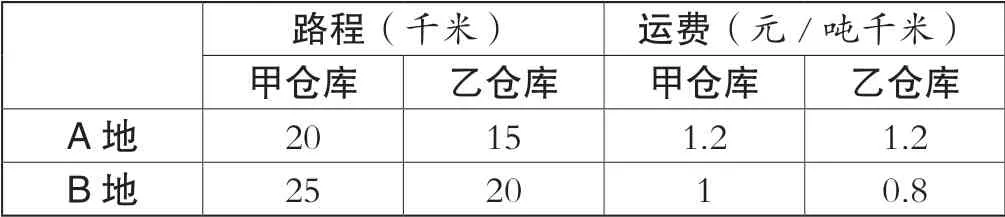
路程（千米） 运费（元/吨千米）甲仓库 乙仓库 甲仓库 乙仓库A地 20 15 1.2 1.2 B地 25 20 1 0.8

问：（1）设甲仓库运往A地水泥x吨，用含x的代数式表示乙仓库分别运往A、B两地多少吨；

（2）当甲、乙两仓库各运往A、B两工地多少吨水泥时，总运费y最小？最小总运费是多少？

学生活动：在独立思考的基础上展开小组讨论：1.如何列代数式？2.如何借助代数式解决问题？3.借助（1）所列出的代数式还能提出哪些问题？

教师调控：在个人探究与小组活动过程中，教师需要关注学生在列代数式过程中，能否厘清数量关系，能否恰当地用字母表示未知量，并列出含有该字母的代数式；需要指导学生对列代数式的相关过程做出概括，引导学生提出更多的实际问题，并借助所列代数式解决问题；需要引导学生关注知识的内在关联，对数与代数板块知识进行结构化归纳概括，凸显知识之间的体系关联。（学生展示过程略）

教学意图：借助本环节，让学生经历从不同角度列代数式，并分析归纳列代数式过程的共性。其次，与方程、不等式、函数等相关知识相联系，完整展现代数式作为“重要组成部分”的知识架构作用。

环节二：体会知识作用，提炼方法联系

教师提问：通过解决下列问题，你认为代数式的作用是什么，解决问题的过程中用到了哪些知识和方法？

超市为回馈市民，决定对某种商品进行降价让利活动，现有两种方案：（1）分两次降价，每次降价率不同。（2）分两次降价，每一次降价率是方案一中两次降价率的平均数。以上两种方案，哪一个方案对消费者优惠力度更大？

学生活动：在独立思考的基础上以小组为单位合作探究：1.解决问题的关键是什么？2.如何借助代数式解决问题？3.解决问题的过程中用到了哪些知识和方法？

教师调控：教师主要关注学生探究过程，指导学生用数学符号表示已知量和未知量；引导学生对所列代数式进行运算、推理等操作，引导学生分析问题的共性，归纳方法。（学生展示过程略）

教学意图：其一，本题不含数字或字母，需要学生将实际问题转化为数学问题，用数学符号表示问题中的量及量之间的关系，感悟用代数式解决问题的一般性。其二，设置知识明线和思想方法暗线两条主线，促进学生学习由字母或代数式所代表数值的不确定性产生的分类讨论思想。

四、教学反思与感悟

1．选择合适的素材，确定学习的研究载体

所谓合适，就是有研究的价值，对学生理解数学有重大作用的，有着典型性、生长性、拓展性等特点，有利于学生感悟实际问题数学化的一般过程：“实际问题→量及其关系→代数式”，发展数学抽象能力。“代数式”在初中数学课程体系中看似不起眼，但其学科价值却影响深远，对代数式的研究贯穿代数学的整个过程。能够有意识地列代数式，并借助相关运算、推理解决问题，标志着符号意识、代数推理、数学建模等核心能力发展至较为成熟的阶段。

2．创设有效的课堂活动，推动学生的素养发展

课堂活动的创设要始终围绕“发展学生核心素养”这一主题。本节课中，着眼于发展学生符号意识、数学推理与运算、数学建模应用等核心能力。一是，有意识地创设问题情境，引领学生用字母表示数，列代数式表示量及量之间的关系，充分感悟引入数学符号的意义，发展学生数学抽象能力。二是，通过问题设置，推动学生对所列代数式进行运算、推理，经历以代数式为核心构建方程、不等式、函数等模型解决问题的完整过程，同时帮助学生将数学知识的结构化，理解不同知识板块间的内在联系。三是，通过引导学生借助所列代数式解决更多问题，发展学生发现问题、提出问题的能力。

3．搭建思维的发展平台，实现数学的智慧进步

教会学生“想问题”的顺序和方法，这是数学教学“质的突破”，使学生思维的生长有章可依，有法可鉴，有据可循。在本节课，始终贯穿“发现量及其关系→表示量及其关系→应用量及其关系”这条主线，这是代数式研究的核心体现。数学知识的学习以此为主轴有序展开：方程研究不同代数式之间的相等关系，不等式研究不同代数式之间的不等关系，函数——研究代数式与其所含字母之间的相互对应、相互依存的关系。学习它的价值就是使学生从“做题”到“明理”，在更广阔的视域内“看问题”。为了获得“代数式”，需要建立量之间的关系，关系复杂时，需要借助一定手段——列表、画图。这些手段就是在帮助学生更加有序且有效地“想问题”。