Improving the Young’s modulus of Mg via alloying and compositing -A short review

Hailong Shi ,Chao Xu ,Xiaoshi Hu ,Weimin Gan ,Kun Wu ,Xiaojun Wang,∗

a National Key Laboratory for Precision Hot Processing of Metals,Harbin Institute of Technology,Harbin 150001,PR China

b Center for Analysis and Measurement,Harbin Institute of Technology,Harbin 150001,PR China

c GEMS at MLZ,Helmholtz-Zentrum Hereon Lichtenbergstrsasse 1,Garching D-85748,Germany

d School of Materials Science and Engineering,Harbin Institute of Technology,Harbin 150001,PR China

Abstract Lightweight,high-modulus structural materials are highly desired in many applications like aerospace,automobile and biomedical instruments.As the lightest metallic structural material,magnesium (Mg) has great potential but is limited by its low intrinsic Young’s modulus.This paper reviews the investigations on high-modulus Mg-based materials during the last decades.The nature of elastic modulus is introduced,and typical high-modulus Mg alloys and Mg matrix composites are reviewed.Specifically,Mg alloys enhance Young’s modulus of pure Mg mainly by introducing suitable alloying elements to promote the precipitation of high-modulus second phases in the alloy system.Differently,Mg matrix composites improve Young’s modulus by incorporating high-modulus particles,whiskers and fibers into the Mg matrix.The modulus strengthening effectiveness brought by the two approaches is compared,and Mg matrix composites stand out as a more promising solution.In addition,two well-accepted modulus prediction models (Halpin-Tsai and Rule of mixtures (ROM)) for different Mg matrix composites are reviewed.The effects of reinforcement type,size,volume fraction and interfacial bonding condition on the modulus of Mg matrix composites are discussed.Finally,the existing challenges and development trends of high-modulus Mg-based materials are proposed and prospected.

Keywords: Elastic modulus;Mg alloy;Mg matrix composite;Modulus prediction model;Mechanical properties.

1.Introduction

Magnesium (Mg) and Mg alloy are well-known for their low density,easy recyclability,excellent damping and machinability while being limited in terms of their low elastic modulus,low absolute strength and poor corrosion resistance [1,2].With the advance of modern industries like aerospace,automobile,weaponry,etc.,metallic materials that possessing low density and high stiffness are highly desired to save energy and reduce the emission of greenhouse gas.Thus,increasing the elastic modulus of Mg-based materials is regarded as one of the most crucial issues in the past decades when developing novel high-performance Mg-based materials.However,because elastic modulus is an intrinsic property for a certain material system,although a great amount of effort has been invested,limited modulus increment was obtained either by alloying or by fabrication of composites.Thus,it is still a bottleneck to fabricate high-modulus Mg-based materials.

Microscopically speaking,the elastic modulus is dependent on the interatomic binding forces.As a result,it is not sensitive to heat treatment,manufacturing process or minor compositional variations.To increase this value,one needs to introduce certain components into the system which can alter the interactions between neighboring atoms.Currently,there are mainly two types of methods to increase the elastic modulus of Mg significantly: (i) Developing Mg alloys by incorporating alloying elements like Al [3,4],Li [4,5],Ge[6],Pb [3],Si [7-9],Y [10],Ag [6],Zn [4] and rare earth(RE) elements [11] into the Mg matrix;(ii) Fabricating Mg matrix composites by incorporating high-modulus reinforcements like ceramic particles (Al2O3[12],SiC [13-16],B4C[17],AlN [18],WC [19],MgO [20],TiB2[21],Si3N4[22],ZrO2[23],TiC [21],SiO2[24],etc.),whiskers (Mg2B2O5[25],Al18B4O33[26-30],Al2O3[12,31],SiC [31],etc.) and long fibers (C [32,33],Ti [34],Al2O3[12],TiNi [35],etc.)into the composite systems.Although many Mg-based materials have been developed,limited modulus increment was realized,especially in Mg alloys.Normally,Mg alloys can increase Young’s modulus by less than 25%compared with pure Mg,much smaller than the induced strength increment by the same fraction of alloying elements.For Mg matrix composites,the modulus enhancement is relatively higher than Mg alloy,and the strengthening efficiency depends greatly on the employed reinforcements.Currently,Mg matrix composites reinforced with continuous fibers possess relatively the highest modulus,while Mg matrix composites reinforced with whiskers and particles obtained much less modulus increment.Anyway,the upper limit of Mg matrix composites is much higher than that of the Mg alloys,and fabrication of Mg matrix composites tends to be a more promising way to yield high-modulus Mg based materials in the future.

Motivated by these observations,this review committed to introducing the physical nature of elastic modulus of metallic materials and recalling the development of high-modulus Mgbased materials by fabrication of Mg alloys and Mg matrix composites during the past decades.The mechanisms of elastic modulus strengthening by alloying and composite methods are reviewed.Specifically,high-modulus Mg alloys with various precipitates are introduced,and the microstructure and mechanical properties of Mg matrix composites reinforced with distinct reinforcements are compared in terms of the reinforcement type,size,volume fraction and interfacial bonding conditions between reinforcements and the Mg matrix.Moreover,the merits and limitations of the two well-accepted modulus prediction models proposed for Mg matrix composites are discussed.Finally,the two kinds of high-modulus materials,i.e.,Mg alloys and Mg matrix composites,are compared in the case of elastic modulus strengthening efficiency.The existing challenges and the development trends of highmodulus Mg-based materials are proposed and prospected.

2.The nature of elastic modulus

Modulus of elasticity describes the difficulty of elastic deformation of an object or substance under a specific applied load within the elastic range,including Young’s modulus (E),shear modulus (G),and bulk modulus (B).It is increasingly hard to trigger the elastic deformation of a solid body with the enhanced elastic modulus.Generally speaking,for metallic materials,the elastic modulus refers to Young’s modulus,which defines the tendency of an object to deform along an axis under tension or compression along that axis and is determined as the ratio of normal stress (σ=F/A: force per unit area) to normal strain (ε=ΔL/L: proportional increase in length parallel to the applied force),i.e.,σ/ε[36,37].From a microscopic perspective,however,the elastic modulus is a fundamental property (interatomic binding force) of material and depends essentially on the type of interatomic binding forces.This binding force differs with the interatomic bonding category,such as homovalent,ionic,and metallic bonds.As a result,the metallic bonds dominate Young’s modulus of Mg alloys because they prevail in metallic materials.When the elastic deformation occurs,the interatomic distance increases or decreases,leading to the variation of the bonding energy.Thus,the factors which influence the interatomic binding force like bonding types,crystal structure,chemical composition,microstructure and temperature can all lead to variation of elastic modulus of the material.

The stiffness of a rigid body is defined by the elastic modulus of the component material,which acts as one of the most critical material characters for structural materials.In most applications,this value determines the bearing limit of the instrument,because once yielding occurs,the structural component fails.Thus,much attention was paid to this character when designing and developing a new kind of structural material.

The modulus of elasticity depends on the interatomic binding forces and is governed by the interactions between the electrostatic attractive and repulsive forces.At the atomic level,it describes the resistance of atomic bonds to bending or stretching.This potential energy (denoted as U) could be described by the classical Lennard-Jones potential [38]:

whereris the interatomic distance,εis the bond energy,σdenotes the finite distance at which the intermolecular potential energy between the two neighboring atoms is zero.

As shown in Fig.1,we set the repulsive force as positive and the attractive force as negative.The depth of the potential energy well just equals the bond energy and is also denoted asεin this figure.The minimum of the potential energy is from the first derivative of the potential,i.e.,dU/dr=0,this happens when the potential energy equals to -ε,at this time,theris just at the equilibrium spacing ofr=ro=1.12σ.Since the interatomic forceFequals to-dU/dr,in other words,the slope of theU-rcurve,it could be deduced that a high elastic modulus arises from a sharper potential well that possesses a more significant slope in the vicinity of the equilibrium spacing.

The elastic modulus is an intrinsic material character and is the function of interatomic bond energy (ε) and the distance between two adjacent atoms (r).To produce a significant modulus increment,one needs to introduce external components into the material system or adopt special processing techniques which could alter the two key characters.Currently,in order to improve the elastic modulus of pure Mg,fabrication of Mg alloys and Mg matrix composites are well accepted to be the two most important methods.

Fig.1.Interatomic potential energy (Ur) as a function of the distance between two adjacent atoms.

3.High modulus Mg alloys

Because elastic modulus is a kind of intrinsic material property and is directly related to the bond strength between atoms in crystalline solids,alloying comes to be a standard method to tailor the elastic modulus of metallic materials[4,6-11,39,40].According to the existence form of alloying elements in an alloy system,they could be classified into two types,i.e.,solid solution and intermetallic compound.

3.1.Young’s modulus of Mg solid solution

There are two types of solid solutions,i.e.,continuous solid solution (the alloying element possesses infinite solid solubility in the alloy system) and discontinuous solid solution (the alloying element possesses limited solid solubility in the alloy system),classified by solute degree of the alloying elements.For instance,for continuous binary alloys like Cu-Ni,Cu-Au and Ag-Cu,the elastic modulus changes typically linearly with the variation of the atomic fraction of the alloying elements [39].Young’s modulus increases when the alloying elements possess a higher average modulus than the matrix metal.The opposite effects will be generated when the lower modulus elements are adopted.Differently,for a discontinuous solid solution,the alloying elements normally possess small content in the composites in two ways.Some of the large alloying atoms take the place of the matrix atoms,and other small alloying atoms like N,H,C,B,etc.,may occupy the interstitials of the matrix alloy.Despite their existence form in the alloy systems,no significant modulus change is expected.As indicated by the Eq.(1),the elastic modulus derives from atomic bonding strength (εin Eq.(1)) and atomicseparation distances (rin Eq.(1)).Because the alloying elements in discontinuous alloys do not change the bonding type or atomic spacing appreciably,the modulus of the alloy will not change dramatically.Therefore,neither continuous or discontinuous alloys results in great modulus change to the pure Mg.

For Mg solid solution,few experimental result is available [3,5,41] and the effects of different alloying elements on the elastic properties of Mg was investigated by Ganeshan et al.[39] using the first-principles calculations.Specifically,a supercell consisting of 36 atoms (35 Mg and 1 X atom,corresponding to 2.77 at.% X) was employed for the calculations,and the elastic properties of pure Mg and 12 kinds of Mg-X (Al,Ca,Ba,Cu,Li,Ni,K,Pb,Si,Ge,Y,Zn,belong either to thes-block,p-block ord-block of the periodic table) solid solution is calculated.Table 1 displays the calculated and some experimental elastic properties of pure Mg and Mg-X alloys.It should be noted that the experimental elastic modulus for Mg-Al,Mg-Li,Mg-Zn and Mg-Pb alloys were measured at several compositions and have been extrapolated to Mg-(2.77% at.% X) for comparison herein.The authors stated reasonable-level of accuracy of the calculated values in their work because the average difference between the calculated and experimental data is smaller than 8%.It was observed that the elastic properties of the Mg-X alloys are affected by the valence shell electrons of the alloying elements.Specifically,the addition of solute atoms belonging to thes-block results in a lower bulk modulus than the addition ofp-andd-block elements.Betweenp-andd-block elements,the former have a lower bulk modulus value except in the case of element Y.The authors attribute this exception to the fact that the Y element has only 1delectron.However,although there exists strong dependence of the bulk modulus on the valence electrons of the alloying element added to Mg,such dependence is absent in the case of shear modulus.

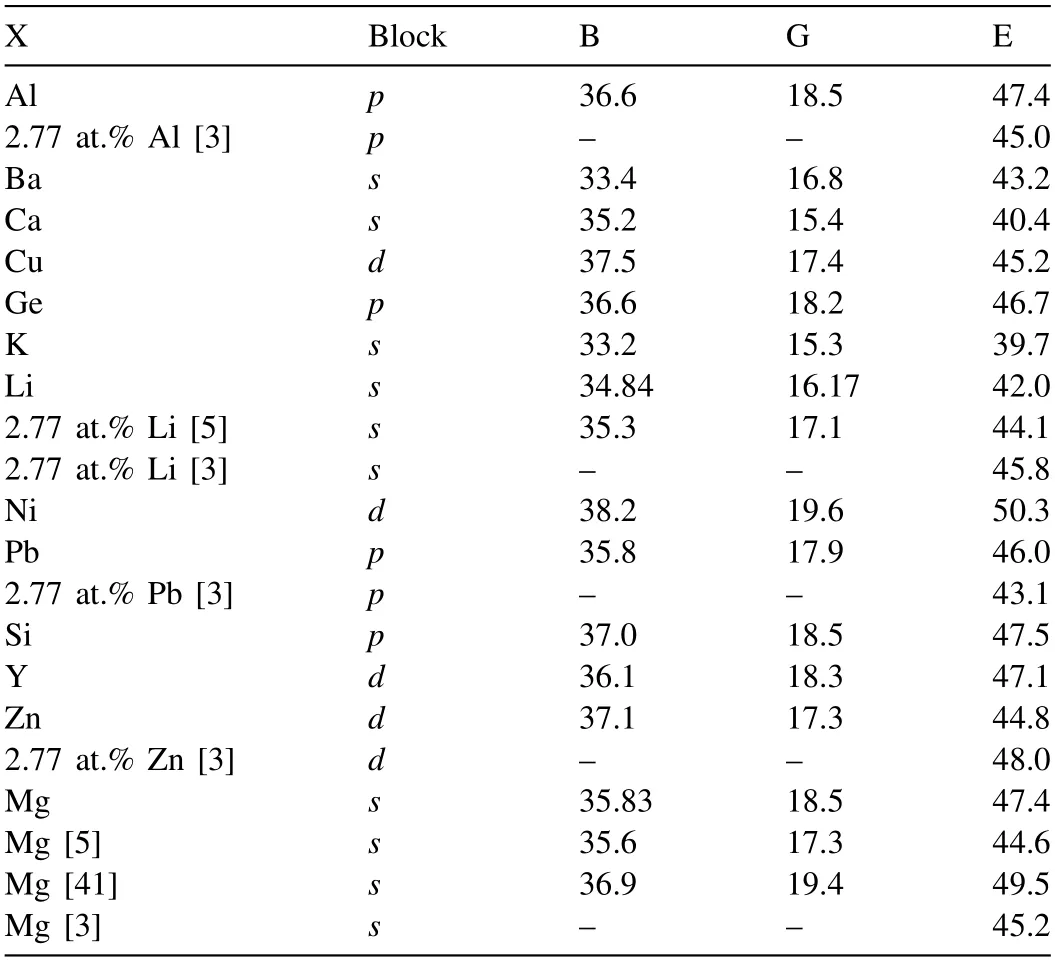
Table 1 Calculated and experimental elastic properties (GPa) of pure Mg and Mg-X alloys [39].

Fig.2.OM images of (a) Al2Gd and (b) Al2Li3 phases in the Mg-Gd-Zn-Zr-Ag-6Al-5Li alloy [4].The insets are TEM images of the indicated phase and corresponding SAED patterns.

3.2.Young’s modulus of Mg alloys reinforced by precipitated second phases

The elastic modulus of Mg alloys does not vary much by producing a continuous or discontinuous solid solution.In more cases,Mg alloys are consisted of a solid solution matrix with binary or ternary second phases because of the low solubility of alloying elements in Mg.At present,the most effective way to increase the elastic modulus of Mg by alloying is to add specific alloying elements into Mg to generate a large number of high-modulus precipitates (second phases)in the alloy.These second phases work as reinforcements in the alloy system so that those with high strength,high elastic modulus,good compatibility and high-temperature stability are favored.For instance,Hu et al.[8] investigated the effects of Si addition (1.0 wt.%) on microstructure and mechanical properties of Mg-8Gd-4Y-Nd-Zr alloy.The results indicated that the added Si led to the formation of high-modulus Mg2Si and (RE+Si)-rich particles,which enhanced Young’s modulus of the alloy by 7 GPa.Tu et al.[4] studied the effects of Al and Li additions on the elastic modulus and ductility of Mg-Gd-Zn-Zr-Ag alloy and obtained an increment of 18.2% on the elastic modulus by the Mg-Gd-Zn-Zr-Ag-6Al-5Li alloy.The high-modulus Al2Li3(125.39 GPa) and Al2Gd(144.23 GPa) phases,as shown in Fig.2,were attributed as the main reasons for the increased elastic modulus.Furthermore,Zhao et al.[10]fabricated Mg-1.3Y-0.8Zn-6.4Al-16.7Li(at.%) alloy with increased Young’s modulus of 52.9 GPa compared with the 46.9 GPa of the Mg-1.3Y-0.8Zn alloy,and the authors attribute the enhanced Young’s modulus to the added Li in solid solution and the formation of highmodulus Al-Li and Al2Y phases.Zhao et al.[9].investigated the effects of Si element on Young’s modulus and damping capacity of the extruded Mg-Gd-Y-Zn-Mn alloy.Fig.3 shows the SEM micrographs of the Mg-Gd-Y-Zn-Mn and Mg-Gd-Y-Zn-Mn-Si alloys.It showed that the long period stacking ordered (LPSO) phase was greatly reduced after the Si addition.Instead,a large number of (RE+Si)-rich particles were formed.Due to the contribution of the high-modulus second phases,the elastic modulus of the as-extruded Mg-Gd-Y-Zn-Mn alloy increased to 49.3 GPa,8 GPa greater than that of the as-extruded pure Mg.

In general,the multi-element alloy is designed and fabricated to increase the elastic modulus of Mg alloy by the formation of high-modulus second phases.Table 2 displays Young’s modulus of some typical high-modulus Mg alloys and the corresponding in-situ formed second phases.It is seen that,although the formed second phases all possess higher elastic modulus than the Mg matrix (as-cast～41 GPa,asextruded～45 GPa),their elastic modulus (normally less than 200 GPa)is not so high as the externally added second phases like ceramic particles,whiskers and fibers,which may possess elastic modulus as high as 480 GPa for the SiC particles,for instance.Moreover,since the alloying elements used are normally non-infinite solid solution elements,they possess a low content in the Mg alloy system,which can produce low content of second phases in the alloy.As a result,according to the rule of mixtures (ROM),Young’s modulus of the Mg alloy cannot increase much by low fraction of the in-situ formed high-modulus second phases.

Table 2 Young’s modulus of typical high-modulus Mg alloys and the corresponding second phases.

Table 3 Young’s modulus of carbon fibers in two feature directions.

Fig.3.OM images and SEM images of the as-extruded Mg-Gd-Y-Zn-Mn (-Si) alloys [9].(a)(c) The Mg-7Gd-4Y-2Zn-0.5Mn alloy,(b)(d) the Mg-7Gd-4Y-2Zn-0.5Mn-0.8Si alloy.

Fig.4.Different types of reinforcements employed in high-modulus Mg matrix composites.(a) Particles,(b) short fibers and whiskers and (c) continuous fibers.

It is worth mentioning that,along with the formation of precipitates in different types,sizes and shapes,distinct types of phase boundaries could be generated and termed as coherent,semi-coherent and incoherent phase boundaries according to the matching degree between the metal matrix and the precipitates [42].The coherent phase boundaries create small or near-zero lattice distortion and enable the perfect load-transfer between the matrix and the precipitates.Thus,coherent phase boundary has nearly no effect on the elastic modulus of the alloy system.Differently,pores and intense lattice strain could be generated at the semi-coherent or incoherent phase boundaries.As a result,the elastic modulus of the alloy will be decreased [43,44].However,because the phase boundaries normally only account for a very small volume fraction of the alloy system,they hardly affect the elastic modulus of the alloy system and could be ignored when conducting the modulus calculation.

4.High modulus Mg matrix composites

As mentioned above,introducing high-modulus second phases into Mg by alloying is restricted by many conditions and can only bring limited increment to the final Young’s modulus.Differently,fabrication of Mg matrix composites,wherein the high-modulus metal or non-metal reinforcements are incorporated into pure Mg or Mg alloy systems,could increase the elastic modulus of Mg to a large extent.On the one hand,there are fewer limitations to the selection of the employed reinforcements than alloying elements in a Mg alloy system.Although we can also use different types of alloying elements so as to produce specific precipitates in the alloy system,the type and amount of the precipitates are strictly restricted by the added alloying elements.For Mg matrix composites,we also need to take some characters like the wettability and the chemical stability of the reinforcements into consideration so that they are compatible in the composite system.Many strengthening agents are satisfied,and Mg matrix composites reinforced with various reinforcements were prepared with the purpose of increasing the mechanical and physical properties of the Mg matrix composites in the past decades.On the other hand,the content of the added reinforcements in the Mg matrix composites is normally much larger than that of thein-situformed second phases in Mg alloys.This is because that the solubility of alloying elements in Mg alloy is normally small.Correspondingly,the volume fraction of the precipitates is also small since they are proportional to the content of the alloying elements.Differently,for the Mg matrix composites,there is no limit to the content of the added reinforcements if we do not pursue a uniform distribution of the reinforcements in the Mg matrix.Notably,the comprehensive mechanical properties of the Mg matrix composites is highly related to the distribution of the reinforcements.It is well accepted that a uniform distribution of reinforcements in the composites is usually pursued to eliminate the strength-ductility trade-off,especially in Mg-based materials.Thus,to avoid early failure of the material due to the formation of the reinforcement clusters,the volume fraction of the reinforcement is also limited,especially for the nanosized reinforcing particles.In general,the volume fraction of the micro-sized particular reinforcements is less than 20%,and it is challenging to successfully incorporate more than 5 vol.% nano-sized particles into the Mg matrix composites,although many advanced fabrication methods such as semi-solid mechanical stirring[45-47],high-energy ultrasonic vibration processing[48-50],molecular mixing[51-53],powder metallurgy [54,55],etc.,were employed to promote the dispersion of reinforcements in the composites.

According to the shape of the reinforcements,they could be mainly classified into three types,i.e.,particles,whiskers(or short fibers) and fibers (continuous long fibers).Fig.4 illustrates the schematic diagram of Mg matrix composites reinforced by the three types of reinforcements.The incorporated reinforcements do not change the interatomic binding forces between the matrix atoms.They tailor the elastic modulus by introducing high Young’s modulus constituents into the system.Thus,Young’s modulus of the Mg matrix composite is greatly influenced by the features of the employed reinforcements.

4.1.High modulus Mg matrix composites reinforced with particular reinforcements

Particular reinforcements are mostly used in Mg matrix composites,such as Al2O3,SiC,B4C,AlN,NbN,WC,ZrC,MgO,TiB2,Si3N4,ZrO2,MoS2,Mo2C,ZrB2,TiC,SiO2,etc.[12-16,21,56-58].For high-modulus Mg matrix composites,particles with high modulus like SiC (Young’s modulus of 480 GPa) and B4C (Young’s modulus of 450 GPa) are commonly employed because of their advantages such as high wettability in Mg,high stability and low cost.For instance,Wang et al.[16] fabricated SiC particles reinforced AZ91 composites with SiC volume fraction of 5-20% by an ultrasonic vibration assisted mechanical stirring process.The obtained SiC/AZ91 composites possess uniform distribution of SiC particles both in the macro and micro scale,as shown in Fig.5 [16].The results also evidenced that the employed ultrasonic treatment assisted semi-solid mechanical stirring method is effective to disperse the microparticles in the Mg matrix composites.

Fig.5.SEM-SE micrographs of SiC particles reinforced AZ91 matrix composites [16].(a) Low magnification,(b) high magnification.

Fig.6.Typical tensile properties as a function of the volume fraction of the added SiC particles.(a) Yield strength (YS) and ultimate tensile strength (UTS),(b) elongation and elastic modulus [16].

Fig.6 displays the yield strength (YS),ultimate tensile strength (UTS),elongation and elastic modulus (E) change curves as a function of the volume fraction of the reinforced SiC particles.It is seen that the YS and UTS of the composites increase linearly with the increased SiC volume fraction(Fig.6a).Interestingly,Young’s modulus of the SiC/Mg composite is proportional to the strength while negatively proportional to the elongation of the composites,as shown in Fig.6b.It should be noted that the YS,UTS and E possess the same increasing trend when the volume fraction is smaller than 15 vol.%.When further increased the volume fraction of the SiC particles,the UTS exhibited lower strengthening efficiency when the volume fraction of SiC is high (for example,20%),while the composite still possesses high strengthening potential for Young’s modulus.The dropped UTS strengthening efficiency of high-volume particle reinforced Mg matrix composites is always observed due to the inevitable particle agglomeration at high volume fraction.Differently,the E value still possesses the same increasing tendency as that of the low volume fraction.The Young’s modulus of the SiC/AZ91 composite increased to 72 GPa when the volume fraction of the SiC particles increased to 20%.This result evidenced that the elastic modulus of particle reinforced Mg matrix composites is dominated by the incorporated particle content and is not sensitive to the dispersion condition of the particles in the composites.

In summary,it is feasible to increase the elastic modulus of Mg by introducing high-modulus particles into the Mg matrix.However,it is still difficult to realize significant strengthening effect since there is a limit to the volume fraction of the incorporated particles.Normally,for micron particles reinforced metal matrix composites,the maximum volume fraction of the reinforced particles is around 20%.Serious particle agglomeration may occur when too many particles are incorporated,which may deteriorate the mechanical properties of the composites greatly since the particle clusters could work as the nucleation sites for the micro-cracks in the composites.

Fig.7.(a) SEM-BSE image of the as-cast Al18B4O33W/GWZ1031K composite,(b) EDS spectrums taken from point P in Fig.7(a),(c) and (d) SEM-SE images of the as-cast Al18B4O33W/GWZ1031K composite [26].

4.2.High modulus Mg matrix composites reinforced with whiskers

Whisker is one of the most important reinforcements for metal matrix composites (MMCs) [25-30,59].It could be classified into two types,including organic whiskers like Butyl Acrylate-Styrene [60],PHB whiskers [61],and inorganic whiskers such as Mg2B2O5[25],Al2O3[31],SiC[62],SiO2[31] and Al18B4O33[63],etc.For elastic modulus strengthening,ceramic whiskers are usually adopted since they possess relatively higher Young’s modulus,and more importantly,good compatibility with the matrix alloy like Al,Mg,Ti,etc.As for Mg matrix composites reinforced with ceramic whiskers,they were usually fabricated to increase the stiffness as well as strength of Mg or Mg alloy.Chang et al.[26]fabricated Al18B4O33/Mg-10Gd-3Y-1Zn-0.4Zr composites by squeeze casting (as shown in Fig.7) and investigated the microstructure,interfacial characteristics,mechanical properties and fracture behavior of the composites systematically.The results indicated that the integration of high strength (YS=364± 13 MPa) and high modulus (77.8±2.1 GPa) was obtained.

Chen et al.[25] investigated the microstructure and interface of a Mg2B2O5whisker reinforced Mg matrix composite.They found that the Young’s modulus of the Mg2B2O5/AZ91 composites increased to 54 GPa because of the addition of the whiskers.Besides,the MgB4O7particles and the globular Mg2Si particles were observed within the Mg2B2O5whisker,and at the interface between the Mg2B2O5whiskers and the Mg matrix,respectively.The MgO and MgB2phases formed at the matrix-whisker interface during the vacuum-gas pressure infiltration process due to the interfacial reaction [25].Zheng et al.[27] investigated the microstructure and mechanical properties of aluminum borate whisker reinforced AZ91 composites (Al18B4O33w/AZ91) fabricated by squeeze casting.The results showed that the tensile properties and Young’s modulus of the composite increased greatly compared with the matrix alloy.Interestingly,detailed microstructure observations found that a thin MgO layer was formed at the whisker-matrix interface by the chemical reaction:

Fig.8.Interfacial structure of the Al18B4O33w/AZ91 composites after exposure at (a) 400 °C for 10 h,(b) 400 °C for 30 h and (c) 600 °C for 10 h [29].

Fig.8 shows the TEM micrographs of the interfacial structure of the Al18B4O33w/AZ91 composite after exposure at different temperatures.When the composites were exposed below the liquidus temperature of the matrix,a thin MgO layer formed in spite of the exposure duration since the dense MgO layer prevented the further reaction between the matrix and the whisker.The Young’s modulus of the Al18B4O33w/AZ91 composites also showed that the as-cast Al18B4O33w/AZ91 composite increased significantly than the AZ91 alloy.This may be because that the formed thin MgO layer enhanced the interfacial bonding between the matrix alloy and the reinforcements and generated potent interatomic bonds with both constituents [64,65].

However,when the Al18B4O33w/AZ91 composites were exposed at temperatures above the liquidus point of the matrix for a long period,as shown in Fig.8c,intense interactions occurred at the matrix-whisker interface and a thick MgO layer was generated.It is reported that the thick reaction layer may induce notches on the whisker surface.Moreover,the larger MgO particles with sharp-edge closer to the matrix-reaction layer could also induce stress concentrations under an applied load[29].Thus,the as-formed thick reaction layer could deteriorate the strength of the employed whiskers and eventually decrease the comprehensive properties of the composites.

4.3.High modulus Mg matrix composites reinforced with fibers

Except for the cost-effective non-continuous particles and whiskers,Mg matrix composites reinforced with fibers like C,Ti,B,Al2O3,and SiC were also investigated by many researchers [31,33,66-69].Along with the strength improvement,many of the fiber-reinforced Mg matrix composites were found to possess drastically increased Young’s modulus compared with the matrix Mg alloy.Notably,the volume fraction of fibers (up to 60%) in the composites is normally higher than that of the non-continuous reinforcements,and the as-fabricated composites possess much advanced Young’s modulus.For instance,Liu et al.fabricated aluminum silicate short fiber ((Al2O3-SiO2)sf) reinforced AZ91D matrix composites by the pressure infiltration method,the result showed that the Young’s modulus of the (Al2O3-SiO2)sf/AZ91D composites increased from 38.5 GPa to 61 GPa (58% higher than the AZ91D alloy) [31].

Among all the continuous fibers reinforced Mg matrix composites,carbon fiber (Cf) reinforced Mg matrix composites (Cf/Mg) were mostly investigated,and they were reported to possess the highest specific Young’s modulus among all the metallic materials [66,70].Carbon fiber offers excellent mechanical and physical properties such as high tensile strength(2-7 GPa),high Young’s modulus (200-900 GPa),low density(1.75-2.20 g/cm3),low thermal expansion and super electrical and thermal conductivity (～800 Wm-1K-1) [71-76].Thus,it is attractive to develop lightweight,high-performance Mg matrix composites adopting Cfas the reinforcement.Besides,the large ratio of the long fiber together with the aligned fiber arrangement could contribute to the anisotropic properties of the composites,in other words,the as-fabricated composites may possess diverse mechanical or physical properties in distinct sample directions (parallel or perpendicular to the axial direction of the employed fibers).Moreover,carbon fibers possess good high-temperature chemical stability and do not react with molten Mg,which enables the fabrication of Cf/Mg composites through the melt processing techniques.

Recently,continuous carbon fiber reinforced metal matrix composites (CF-MMCs) are usually fabricated by gas pressure infiltration [32,77],low pressure infiltration [67,76]and pressure infiltration techniques [78,79].Specifically,preforms of carbon fibers are prepared by entangling or winding the long fibers unidirectionally to a designed shape by a computer numerical control (CNC) winding machine.After that,the molten metal is pressed into the preforms making the molten metal to get into the gaps between adjacent carbon fibers.Golyandin et al.[33] fabricated long unidirectional carbon fibers reinforced Mg matrix composites with a fiber volume fraction of 30%.The obtained Cf/Mg composites possess an impressive Young’s modulus of 275 GPa along the fiber axial direction.Song et al.[67] fabricated unidirectional and orthogonal woven carbon fibers (T700 and M40) reinforced Mg matrix composites by the pressure infiltration method.The as-fabricated unidirectional T700/AZ91D and M40/AZ91D composites possess experimental Young’s modulus of 156 and 242 GPa,respectively,along the axial direction.Fig.9 displays the typical fractographs of Cf/Mg composites,it is clearly seen that the gaps between adjacent carbon fibers are filled with the matrix alloy,and some individual fibers were pulled out during the tensile tests.

Fig.9.Fracture surfaces of the M40/AZ91D composite [67].

Notably,the anisotropic Young’s modulus of Cfmay affects the elastic modulus of Cf/Mg composites greatly.As displayed in Table 3,for instance,the T700 fibers possess a Young’s modulus of 230 GPa along the axial direction.In contrast,in the transverse direction,the fiber only exhibits a Young’s modulus of 8.2 GPa.The great modulus anisotropy is not desired sometimes and the woven carbon fibers were employed to increase the symmetry of the mechanical performance of the Cf/Mg composites [67].

Table 4Theoretical and experimental values of mechanical properties of Cf/Mg [67].

For Mg matrix composites,the Young’s modulus could be greatly improved by load transfer from the matrix to the reinforcement during the elastic deformation process [80-82].As a result,the quality of the interface between the matrix and the reinforcements is of great importance for determining the load-transfer efficiency.In order to obtain high load-transfer efficiency,moderate chemical interfacial reaction is favored since high-strength interface could be produced by the chemical bonding [83-85].However,excessive chemical reaction should be avoided to prevent the integrity damage to the reinforcements.

Although carbon fibers do not react with Mg at high temperatures,they could react with some alloying elements(Al,Si,etc.) in Mg alloys.In the T700/AZ91D and the M40/AZ91D composites prepared by Song et al.[67],aluminum carbide (Al4C3) were observed by TEM characterizations at the Mg-Cfinterfacial regions,as shown in Fig.10.It was found that the amount of the reaction products is related to the graphitization degree of the used carbon fibers.For M40 carbon fibers with higher graphitization degree,fewer Al4C3were observed (seen in Fig.10(b)),and they possess smaller size than that in the T700/AZ91D composites (seen in Fig.10(a)).Although medium reactivity could increase the interfacial bonding strength and benefit the mechanical properties of the composites,violent and uncontrollable interfacial reactions should be avoided in Cf/Mg composites since they will deteriorate the mechanical properties of the fibers and then cause great damage to Young’s modulus of the Cf/Mg composites.

4.4.High modulus Mg matrix composites reinforced with CNTs and GNSs

Carbon nanomaterials,including Carbon nanotubes(CNTs),graphene (Gr) and graphene nanosheets (GNSs) are relatively new reinforcements used in composites,especially in MMCs.However,they have attracted great attention from material researchers because of their superior mechanical(high strength,high modulus,etc.) and physical properties(high thermal conductivity,super electrical conductivity,etc.)compared with traditional reinforcements.More importantly,there is no chemical reaction between Mg and carbon materials even at high temperatures,making them the ideal reinforcements for Mg matrix composites.Consequently,liquid processing techniques like squeeze casting,stir casting and pressure infiltration could be employed to prepare carbon materials reinforced Mg matrix composites.For most cases,graphene and carbon nanotubes are picked with the purpose to increase the strength of Mg matrix composites.Accompanied by the strength enhancement,significant increment on elastic modulus always occur to the as-fabricated composites [86-91] because of their outstanding Young’s modulus (～1 TPa [92]).For instance,Liu et al.[88] fabricated CNTs/AZ91D composites by mechanical stirring and high-intensity ultrasonic dispersion processing.The results indicated that Young’s modulus of the CNTs/AZ91D composite increased from 44.3 GPa to 64.3 GPa because of the addition of 1.5% CNTs.Compared with CNTs,GNSs seem to offer higher strengthening efficiency on Young’s modulus.Rashad et al.[89] prepared graphene nanoplatelets (GNPs)reinforced Mg matrix composites via powder metallurgy technique.The as-fabricated composites exhibit superior Young’s modulus,yield strength and failure strain compared with the matrix.Notably,Young’s modulus of the composite increased by 131% due to the incorporation of 0.30 wt.%GNPs,and the authors attributed the higher strengthening efficiency of GNPs in comparison to CNTs to their high specific surface area (GNPs have 12.8 times larger specific surface area than CNTs).

Fig.10.TEM images of (a) T700/AZ91D and (b) M40/AZ91D composites at the interface regions.

The biggest challenge for improving Young’s modulus of Mg by incorporating CNTs or GNSs lies on the dispersion of the nano-reinforcements in the composites.Due to the well-known strong Van der Waals forces between adjacent nano-particles,agglomerations of CNTs or GNSs always occur,which harms the comprehensive properties of the composites.Although Young’s modulus is not sensitive to the microstructure of the composites,the reinforcement clusters could greatly deteriorate the strength and ductility of the composites.Moreover,this kind of clusters exist before they are added into the composites so that nano-pores will be incorporated into the composites during the fabrication process.It is really hard to eliminate these pores by normal processing techniques once they are introduced into the composites,as a result,all the mechanical properties including Young’s modulus could be harmed by the non-uniformly dispersed nanoreinforcements.This is why that the volume fraction of CNTs or other carbon nanomaterials is normally less than 2 vol.%in spite of their fascinating mechanical properties.

4.5.Proposed models for elastic modulus prediction

The ability to correctly predict Young’s modulus of MMCs is crucial to design and fabricate high-modulus materials successfully.In the past decades,several models have been proposed,among which,the Halpin-Tsai model is accepted by many researchers to well predict Young’s modulus of MMCs reinforced with non-continuous reinforcements,including particles,whiskers and short fibers [13,57].This model takes the aspect ratio of the reinforcements into consideration,and Young’s modulus of the composites could be expressed by the following equations:

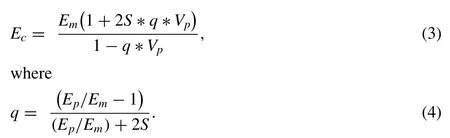
Emis the elastic modulus of the matrix alloy,Epis the elastic modulus of the reinforcement particles,Ecis the elastic modulus of the composite,Vpis the volume fraction of the reinforcement particles,Sis the aspect ratio of the reinforcement particles.

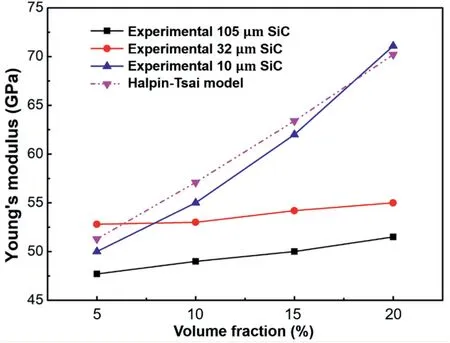
Fig.11.Variation of experimental and predicted Young’s modulus of SiC particles reinforced AZ91D composites(SiCp/AZD)with SiC volume fraction[13,16].

As displayed in Fig.11,variation of experimental and predicted Young’s modulus of SiC particles reinforced AZ91D composites(SiCp/AZ91D)with SiC volume fraction.It is seen that,for each SiC size,Young’s modulus of the SiCp/AZ91D composites increased with the volume fraction of the SiC particles.It should be noted that,when the particle size decreased to 10 μm,the increase rate of the modulus is the highest.However,when we compare the Young’s modulus of composites with the same SiC content,it is found that the Young’s modulus of the composites varies much for different SiC sizes.Specifically,the Young’s modulus increases with the decrease of particle size.In addition,the experimental Young’s modulus of the SiCp/AZ91D composites with SiC size of 10 μm is close to the results of the theoretical values predicted by the Halpin-Tsai model,much higher than the experimental values of the SiCp/AZ91D composites with SiC sizes of 32 μm and 105 μm.This may be because that the smaller particles possess a larger surface area,which will generate a larger reinforcement-matrix interface area in the composites.Because of the mismatch between the matrix atoms and the reinforced particle atoms,the interfacial parts always possess larger internal stress and thus increase the elastic modulus of the composites.Therefore,the Halpin-Tsai model could accurately predict the Young’s modulus of Mg matrix composites when the reinforcement possesses smallsizes.However,the threshold value for the particle size needs to be revealed by further systematical investigations.

Like particular reinforcements,whiskers and short fibers are also non-continuous reinforcements in MMCs.For Mg matrix composites reinforced with different types of whiskers and short fibers,their elastic modulus could also be predicted by the Halpin-Tsai model expressed in Eqs.(3)and(4).However,because whiskers have much larger aspect ratio than the particular reinforcements,they should possess higher modulus strengthening efficiency when they have comparable elastic modulus in comparison with the spherical reinforcements as discussed in part 4.1.In this case,non-continuous fibers are better reinforcements for modulus strengthening in MMCs.

For continuous reinforcements like carbon fibers (Cf),differently,the rule of mixtures (ROM) is normally used to predict Young’s modulus of the composites,and the Young’s modulus of the composite could be predicted by the following equation:

whereEcis Young’s modulus of the as-fabricated composite,Efis the elastic modulus of the incorporated reinforcements,Emis the elastic modulus of the matrix alloy andVfis the volume fraction of the reinforcements.

In this case,theoretically speaking,there is no limit to the elastic modulus of the Mg matrix composites since it is defined by the elastic modulus and volume fraction of the incorporated reinforcements.Table 4 displays the theoretical and experimental values of mechanical properties of two kinds of unidirectionally carbon fiber reinforced Mg matrix composites (Cf/Mg) [67].It is clearly seen that although there is a big gap between the theoretical and experimental tensile strength values,the ROM can well predict Young’s modulus of the Cf/Mg composites.This also evidenced that the elastic modulus is an intrinsic property and is not sensitive to the microstructure (grain size,interface,etc.) of the materials.

5.Comparison between high-modulus Mg alloys and Mg matrix composites

It can be summarized from the above results that both Mg alloys and Mg matrix composites increase their Young’s modulus mainly by introducing high-modulus second phases in the system.The main difference lies in the way of introduction,i.e.,the high-modulus second phases in Mg alloys are formed by precipitation while they are added externally in the Mg matrix composites.Consequently,Young’s modulus of Mg alloys and Mg matrix composites is determined by the mechanical properties of the employed second phases to some extent.Fig.12 displays the densities and Young’s modulus of some typical second phases in Mg alloys and particular reinforcements used in Mg matrix composites.It is seen that the precipitates in Mg alloys all possess relatively low Young’s modulus (lower than 250 GPa) compared with the externally added particular reinforcements.For the latter,most of them possess Young’s modulus (except for BN,SiO2,ZrO2and MoC2) in the range of 300-500 GPa,and is independent of their densities.Normally,density is also an important factor when preparing lightweight,high-modulus Mg-based materials.Thus,the cheap and relatively low-density SiC and B4C particles(as circled with green dashed line in Fig.12) are perfect reinforcing agents for modulus strengthening of Mg matrix composites.

Except for the difference on absolute Young’s modulus of the two types of second phases,they also present distinct achievable volume fractions in the alloy or composite systems.For Mg matrix composites,since the elastic modulus mainly depends on the type and amount of the added particles and is not sensitive to the microstructure of the material,there is no limit to the content of the added particles if we do not take the other mechanical properties like strength,ductility,toughness,etc.,into consideration.While for Mg alloys,the amount of the precipitates is highly constrained by the solid solubility of the specific solute elements.For highmodulus Mg alloys,the reinforcing precipitates are normally binary or ternary intermetallic compounds.Moreover,these high-modulus intermetallic compounds always have transition and rare earth (RE) elements,which possess low solute solubility in Mg alloys.As a result,the volume fraction of the precipitates in Mg alloys is normally small.Constrained by the low modulus and low volume fraction,Mg alloys always possess limited modulus increment compared with Mg matrix composites.

As for high-modulus Mg matrix composites,the modulus is determined by multiple factors,for instance,the reinforcement type (particle,whisker and fiber),the reinforcement size and the matrix-reinforcement interfacial bonding conditions,etc.Fig.13 displays Young’s modulus of Mg matrix composites reinforced with different types of reinforcements as a function of volume fraction.It should be noted that the matrix alloys of these composites could be different,such as pure Mg,AZ91,AZ91D,MB15,Mg-6Zn,etc.Despite the chemical composition and the heat treatment state of the matrix alloys,their Young’s modulus are in the range of 40-45 GPa.Thus,the strengthening effectiveness of different reinforcements could be reflected.

Fig.12.Young’s modulus of common second phases in Mg alloy and reinforcing particles employed in high-modulus Mg matrix composites [4,6,8-10,93-97].

Fig.13.Young’s modulus of Mg matrix composites reinforced with different reinforcements (particles,CNTs/GNSs,whiskers and long fibers) as a function of volume fraction [12-16,25,27,29-31,33,58,67,86,89,98].

It could be seen from Fig.13 that the strengthening effect of CNTs and GNSs on Young’s modulus of Mg matrix composites is significant,obvious modulus increment is realized by a small content of the reinforcement.However,their limited content in the composites restricts the modulus from further climbing.The particular reinforcements possess higher content in the composites (up to 20% in the figure),and their strengthening effect is highly related to the size of the particles.For instance,for SiC particles,the 10 μm sized SiC particles possess relatively the highest strengthening efficiency.The whiskers reinforced Mg matrix composites possess higher Young’s modulus than that reinforced by particular reinforcements.However,this modulus increment is realized by employing high content of whiskers in the composites.Carbon fibers exhibit the highest strengthening effect on modulus among all the reinforcements.It should be noted that the large modulus of Cf/Mg composites is tested along a certain sample direction (parallel to the fiber axial direction),and Young’s modulus of the composites are severely anisotropic.

In the actual production process,Young’s modulus is only one of the mechanical properties we consider when designing a new kind of high-performance Mg-based material.Other mechanical items like strength,ductility and toughness are also crucial to the comprehensive performance of the material.Consequently,the realistic modulus of the present Mg matrix composites is far below the theoretical values predicted by modulus models.The main jobs for material researchers are to tailor the comprehensive performance of Mg-based materials by adopting suitable processing methods and discovering novel reinforcements for the Mg matrix.Most importantly,it is crucial to understand the physical essence of elastic modulus so as to instruct the design and fabrication of high-modulus Mg based materials.

6.Conclusion remarks

1.Elastic modulus is an intrinsic material character and is determined by the interatomic binding forces in the micro scale,i.e.,derived from interatomic bond strength (ε) and the atomic separation distance (r).

2.Mg alloys enhance Young’s modulus mainly by precipitation of high-modulus second phases in the alloy system,while Mg matrix composites realize Young’s modulus improvement by introducing high-modulus particles,whiskers and fibers externally.

3.More significant modulus increments are achieved in Mg matrix composites than in Mg alloys because the adopted second phases offer much higher Young’s modulus,and the reinforcement content is not limited.

4.The Halpin-Tsai model can accurately predict Young’s modulus of Mg matrix composites reinforced with smallsized particles and whiskers.However,the threshold particle size needs to be revealed by further systematical investigations.The rule of mixtures (ROM) is more suitable for Mg matrix composites reinforced with continuous fibers.

5.The interfaces between the Mg matrix and the second phases can affect the Young’s modulus of Mg based materials (especially the Mg matrix composites) by altering the load-transfer efficiency between the two constituents and introducing pores or lattice strain into the system.Chemical reaction is desired to improve the interfacial bonding strength between the matrix and the reinforcements,however,an optimal interfacial reaction degree exists.

6.Young’s modulus of Mg matrix composites is determined by multiple factors,including the reinforcement type (particle,whisker and fiber),size of the reinforcements and the matrix-reinforcement interfacial bonding conditions,etc.One needs to take great care when adopting the reinforcement as well as the processing techniques so as to yield Mg-based materials with an ideal comprehensive mechanical performance.

Conflict of interest

The authors declare no conflict of interest.

Acknowledgments

This work was supported by “National Key Research &Development Program of China” (Grant No.2021YFB3703300),“National Natural Science Foundation of China” (Grant Nos.51971075,51971078,51871074,and 51671066),“National Natural Science Foundation for Young Scientists of China” (Grant No.51801042) and “Fundamental Research Funds for the Central Universities” (Grant No.FRFCU5710000918).