Modeling the optimal compensation capacitance of a giant magnetostrictive ultrasonic transducer with a loosely-coupled contactless power transfer system

Tian LAN, Ping-fa FENG, Jian-jian WANG, Jian-fu ZHANG, Hui-lin ZHOU,2

Research Article

Modeling the optimal compensation capacitance of a giant magnetostrictive ultrasonic transducer with a loosely-coupled contactless power transfer system

1State Key Laboratory of Tribology, Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China2China Ordnance Industry Navigation and Control Technology Research Institute, Beijing 100089, China

The giant magnetostrictive rotary ultrasonic processing system (GMUPS) with a loosely-coupled contactless power transfer (LCCPT) has emerged as a high-performance technique for the processing of hard and brittle materials, owing to its high power density. A capacitive compensation is required to achieve the highest energy efficiency of GMUPS to provide sufficient vibration amplitude when it works in the resonance state. In this study, an accurate model of the optimal compensation capacitance is derived from a new electromechanical equivalent circuit model of the GMUPS with LCCPT, which consists of an equivalent mechanical circuit and an electrical circuit. The phase lag angle between the mechanical and electrical circuits is established, taking into account the non-negligible loss in energy conversion of giant magnetostrictive material at ultrasonic frequency. The change of system impedance characteristics and the effectiveness of the system compensation method under load are analyzed. Both idle vibration experiments and machining tests are conducted to verify the developed model. The results show that the GMUPS with optimal compensation capacitance can achieve the maximum idle vibration amplitude and smallest cutting force. In addition, the effects of magnetic conductive material and driving voltages on the phase lag angle are also evaluated.

Rotary ultrasonic machining; Giant magnetostrictive transducer (GMT); Loosely-coupled contactless power transfer (LCCPT); Electromechanical equivalent circuit; Optimal compensation capacitance

1 Introduction

Hard and brittle materials, represented by ultra-high temperature ceramics and ceramic matrix composites, play a vital role in the aerospace field but they are generally difficult to process using traditional methods. Rotary ultrasonic machining (RUM) is a superior processing technology that applies ultrasonic vibration to the tool to improve the processing performance. The RUM has many advantages in processing hard and brittle materials, including high efficiency, high geometrical accuracy, low cutting heat, long tool life, and low cutting force (Gong et al., 2010; Liu et al., 2012; Wang Y et al., 2014; Wang JJ et al., 2016, 2021). In addition, it is well known that, in RUM, within an amplitude range, the larger the ultrasonic amplitude, the better the processing effect (Liu et al., 2019). The ultrasonic transducer is the crucial component of an RUM system. The transducer that converts the electrical energy into mechanical vibration is usually made of piezoelectric materials.

In addition to piezoelectric materials, giant magnetostrictive material (GMM) emerges as a new and promising energy-converting material for RUM systems. The GMM has the characteristics of high electromechanical conversion efficiency, high power density, and high-quality factor. It can output larger amp litudes with less power and volume (Zhang et al., 2004). The giant magnetostrictive rotary ultrasonic processing system (GMUPS), which uses GMM as the transducer material, can achieve a larger amplitude, and thus a higher material processing efficiency than traditional RUM systems (Zeng, 2013; Cai et al., 2017b).

When performing RUM, the transducer of GMUPS needs to rotate at high speed along with the tool, so it is necessary to use a non-contact method to power the transducer. Using a rotary transformer composed of a pair of coils as a loosely-coupled contactless power transfer (LCCPT) device is usually adopted for power transmission. However, since non-contact power transmission devices will bring a specific inductive load, compensation capacitance is needed to achieve the most efficient energy transmission and maximize amplitude output. Much related research has been done on piezoelectric systems (Jiang and Zhang, 2007; Pang, 2010; Huang and Paramo, 2011; Shen et al., 2015; Zhang, 2019). However, the energy conversion form in the GMM transducer is more complicated than that in the piezoelectric transducer (Zhou et al., 2020b; Ma et al., 2022). The GMUPS needs to be compensated by a unique method. In the past, the compensation methods usually regarded the minimum current frequency as the mechanical resonance frequency and compensated it for electrical resonance (Cai et al., 2017a; Fan et al., 2019). However, these methods have significant deviations, which cause unne cessary energy loss and affect the system's stability.

The unnecessary energy loss that occurs in GMUPS is mainly caused by the core loss (including hysteresis loss and eddy current loss) and skin effect during energy transfer, due to the energy conversion method of the electricity-magnetism-mechanism. These will induce a phase lag between the system's mechanical and electrical parts, indicating a low energy utilization efficiency (Calkins, 1997). In the past, most GMMs were operated at low frequencies, such as sonar systems (Chen, 2015), linear motors (Claeyssen et al., 1997), pumps (Chen et al., 2014), and actuators (Zhang et al., 2004). In those applications, although the core loss and skin effect of GMMs have an impact, they are not as significant as at the ultrasonic frequency. Wakiwaka et al. (1992) found that the phase lag angle between the equivalent mechanical circuit and the electrical circuit was slight under their experimental frequency of 925 Hz. Thus, the phase lag angle caused by the unnecessary energy loss is usually ignored in low-frequency operations because of its small value.

However, in GMUPS, the phase lag angle is much higher than that in low-frequency systems and cannot be ignored. According to research on the performance of metal materials (Wang et al., 2004), both the hysteresis and eddy current losses and the skin effect will cause phase lag in an alternating magnetic field. GMM has essentially the same electromagnetic properties as traditional metal materials, and so the most direct causes of the phase lag are the skin effect and core loss that occur when the GMM and the magnetic permeability material transmit an alternating magnetic field. Since both the core loss and the loss caused by the skin effect increase with frequency, the unnecessary energy loss is significant at high frequencies. The phase lag angle caused by unnecessary energy loss is also significant, and its impact on the system cannot be ignored. Therefore, when analyzing GMUPS, the influence of the phase lag angle must be considered. Zhou et al. (2021) reported a significant difference between the minimum current frequency and the mechanical resonance frequency in GMUPS. This discovery shows that the phase lag angle is significant in the ultrasound system, and a unique compensation method must be used for GMUPS.

In this study, an optimum compensation capacitance model of GMUPS with LCCPT was developed, taking into account the phase lag angle between the mechanical and electrical parts of the system. Combined with the equivalent physical model of cutting load, the load's influence on the performance of capacitance compensation was analyzed. The vibration amplitude measurement without load and drilling experiments were carried out at different compensation capacitances to verify the model. Finally, the effect factors of the phase lag angle were analyzed.

2 Modeling the optimal compensation capacitance

In this section, the electromechanical equivalent circuit model of the GMUPS using LCCPT is first constructed by considering the phase lag angle between the equivalent mechanical circuit and the electrical circuit. Then, the constructed circuit model is mapped using the equivalent method, and the equation of optimal compensation capacitance is derived through the mapped circuit. Finally, the effects of the compensation capacitance on the vibration amplitude of the system under no-load and under loaded conditions are analyzed.

2.1 Illustration of GMUPS structure with LCCPT

The GMUPS, as shown in Fig. 1, can be divided into five parts: giant magnetostrictive transducer (GMT), holder, horn, tool, and LCCPT. The transducer converts alternating current (AC) electrical signals into high-frequency vibration to output mechanical energy. The transducer mainly includes excitation coils, magnetic conductors, permanent magnets, and GMM. The GMM is sliced to reduce eddy current loss and skin effect. The tool holder connects the transducer and the machine tool so that the transducer can rotate together with the machine tool. The horn is used to amplify the amplitude of the mechanical vibration output by the transducer and transmit it to the tool for material processing. The LCCPT is used to provide power to the rotary ultrasonic transducer.

Fig. 1 Structure of GMUPS with LCCPT

The LCCPT includes two parts, the primary and the secondary coil devices. The primary coil is fixed on the machine tool and does not rotate during machining. The secondary coil is fixed on the tool holder housing and rotates with the transducer. A very narrow air gap exists between them, forming an LCCPT through mutual inductance. The primary coil is directly connected with the ultrasonic power supply, and the secondary coil is connected with the excitation coil inside the transducer. The electronic energy is transmitted through electromagnetic induction from the primary to the secondary coil. However, their inductive reactance will affect the system's impedance, limiting the ultrasonic power and vibration amplitude. Therefore, a suitable compensation circuit is essential to maintain the performance of GMUPS (including amplitude, efficiency, and temperature rise).

2.2 Phase lag angle between the mechanical and electrical circuits

To accurately compensate for the electrical resonance, the electromechanical equivalent circuit model of GMUPS needs to be constructed. For the GMT, the electromechanical equivalent circuit is shown in Fig. 2a (Wakiwaka et al., 1992). The left circuit is the electrical circuit, and the right circuit is the equivalent mechanical circuit.is the voltage,1is the resistance of the electrical circuit,1is the inductance of the electrical circuit, and1is the compensation capacitance when the LCCPT is not in use.is the equivalent force, andis the equivalent velocity of the system.

Fig. 2 (a) Electromechanical equivalent circuit without LCCPT and (b) dynamic impedance circle without LCCPT

The impedances of the mechanical part of the electromechanical equivalent circuit of the transducer can be expressed as shown in (Wakiwaka et al., 1992).

When the load stress is less than the proof stress, the strainis proportional to the stress. The final value of the strain is determined by the modulus of elasticity and obeys Hooke's law:

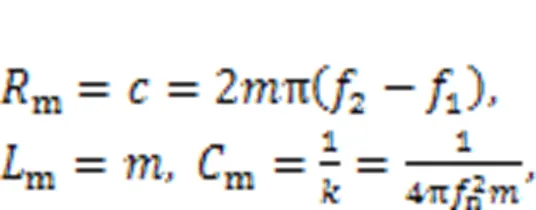
wheremis the mechanical equivalent capacitance,mis the mechanical equivalent inductance,mis the mechanical equivalent resistance,is the mass of the transducer,1and2are the half power frequencies on the impedance circle,is the equivalent damping of the system,is the equivalent stiffness of the system, andnis the mechanical resonance frequency of the system.

There will be a phase lag between the equivalent mechanical circuit and the electrical circuit, due to unnecessary energy loss in energy conversion. For GMUPS, there are two resonance frequencies. One is the mechanical resonance frequency, which is the frequency corresponding to the maximum amplitude; the other is the electrical resonance frequency when the circuit is resistive. Because of the phase lag, the minimum current frequency is not equal to the mechanical resonance frequency, and there is a deviation of tens of Hertz between these two frequencies. Thus, in actual use, we need to compensate the circuit at the mechanical resonance frequency.

Considering the phase lag between the equivalent mechanical and electrical circuits, the electromechanical equivalence coefficientemshown in Fig. 2a can be expressed as a complex, i.e.,

whereemis the real part ofem,emis the imaginary part ofem, andis the angle between the real part and the imaginary part.

The phase lag angle is 2, which is between the mechanical equivalent circuits and the electrical circuits. It can be used to characterize the deviation of the minimum current frequency and the mechanical resonance frequency in the impendence cycle (Zhou et al., 2021). Fig. 2b shows the dynamic impedance circle without LCCPT. The′′′is the dynamic impedance coordinate system andgmutis the radius of the dynamic impedance circle. Due to the influence of the phase lag angle, the transducer cannot achieve mechanical resonance when working at the minimum current frequency.

2.3 Derivation of optimal compensation capacitance model

When using LCCPT, the difference between the mechanical and electrical resonance frequencies is affected by the inductance of the coils in addition to the phase lag angle. To maximize the energy conversion efficiency and the maximum output amplitude of the GMUPS, the mechanical resonance and electrical resonance need to occur at the same frequency. Therefore, a compensation capacitance needs to be connected in series between the system power supply and the LCCPT to adjust the electrical resonance frequency to be closer to the mechanical resonance frequency. Moreover, the modeling of optimum compensation capacitance needs to consider the influence of the phase lag angle and the use of LCCPT.

Finding the optimal compensation capacitance requires an accurate electromechanical equivalent circuit to obtain accurate system impedance. The traditional mapping method usually maps the equivalent mechanical circuit to the resistor-inductor-capacitor (RLC) parallel circuit. But this mapping method does not consideremas a complex number with a phase lag angle. In this study, as shown in Fig. 3, the equivalent mechanical circuit is mapped to an RLC series circuit, and the combination of equivalent capacitance and equivalent inductance is regarded as equivalent reactance. This method can eliminate the modeling error caused by the phase lag angle.

The electromechanical equivalent circuit model of GMUPS with LCCPT is shown in Fig. 3a. The left circuit is the primary circuit of LCCPT, the middle circuit is the secondary circuit of LCCPT, and the right circuit is the equivalent mechanical circuit.eandeare the resistance and inductance of the primary coil of LCCPT, respectively.eis the compensation capacitance on the primary circuit,is the mutual inductance of the LCCPT,sandsare the resistance and inductance of the secondary coil of LCCPT, respectively,cis the resistance of the excitation coil, andcis the inductance of the excitation coil.

The circuit mapping is performed in two steps. In the first step, the right circuit that corresponds to the equivalent mechanical circuit is mapped to the middle circuit, as shown in Fig. 3b. In Fig. 3b,ois the combined resistance of the excitation coil and transducer, andois the combined reactance of the excitation coil and transducer.gmutandgmutare the resistance and reactance of the mechanical mapping, respectively, andgmutis the impedance of the mechanical mapping. They are calculated by the following equations:

Fig. 3 Electro-mechanical equivalent circuit and the mapping circuits: (a) original circuit; (b) circuit after first mapping; (c) circuit after second mapping. Explanations of parameters are given in the following sections

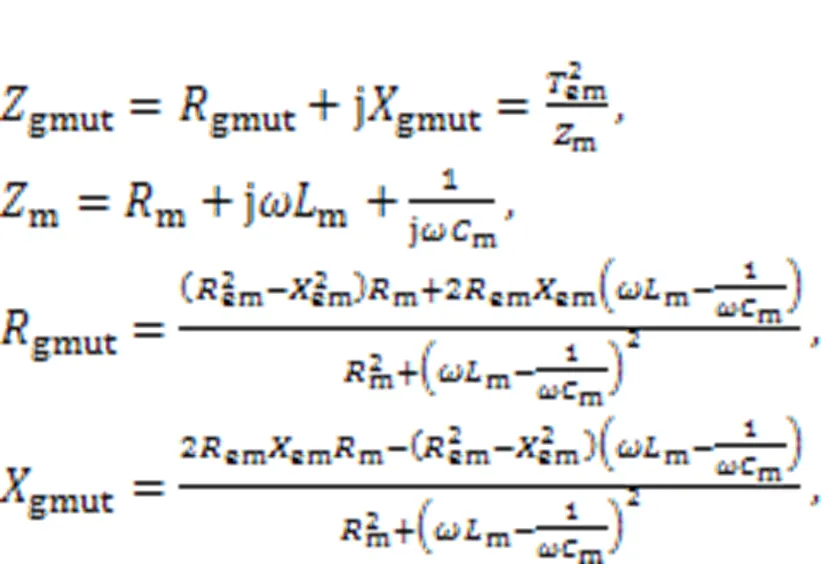
Among them, in Fig. 3b, take the resistance of the new right circuit assec, the reactance of the new right circuit assec, and the overall impedance of the new right circuit assec, then:

In the second step, the new right circuit is mapped to the primary circuit, as shown in Fig. 3c. To facilitate calculations, it is also mapped to an RLC series circuit to obtain the overall equivalent reactance and resistance. In Fig. 3c,motandmotare the mapped resistance and reactance of the new right circuit, respectively, andmotis the impedance of the new right circuit. They can be calculated by the following equations:

When the GMUPS works at the mechanical resonance frequency,

Then,secandseccan be expressed as

In the dynamic impedance circle,

From Fig. 3 and Eq. (5), the overall reactance of the system is

When electrical resonance occurs, the overall reactance is zero. When mechanical resonance and electrical resonance occur at the same time,

whereois the optimal compensation capacitance. Substituting Eqs. (2) and (7) into Eq. (10) and simplifying it, we can obtain an expression foroas follows:

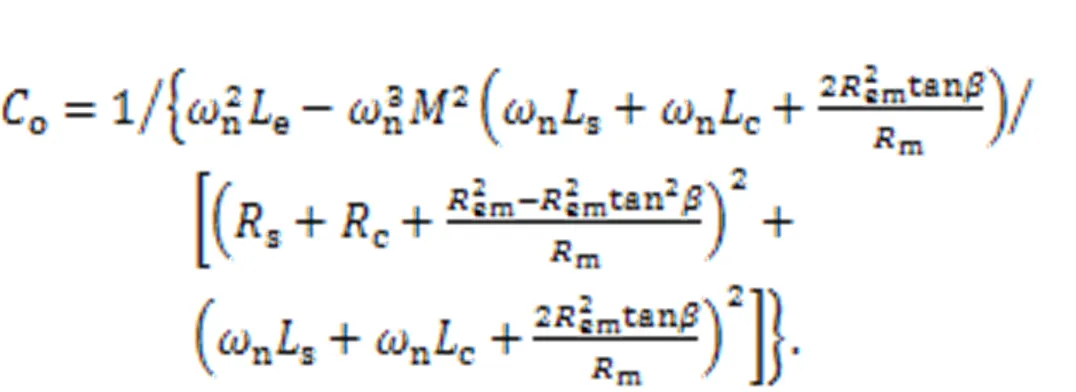
2.4 Performance analysis of optimal compensation capacitance with/without load

Since the optimal compensation capacitance is determined at the mechanical resonance frequency, which is directly affected by the cutting force, the performance of optimal compensation capacitance needs to be analyzed for both no-load and loaded conditions. A theoretical model is developed to analyze the effects of compensation capacitance on the vibration amplitude of GMUPS.

For a general GMUPS, the amplitude prediction models under no-load and loaded conditions were obtained in our previous studies (Zhou et al., 2019, 2020a), respectively, and the amplitude models were:

According to Eqs. (3)‍–‍(5), the impedance circle equation of the GMUPS with LCCPT can be obtained:

Combining Eqs. (7), (12), and (13), the relationship between the vibration amplitudes and compensation capacitance can be obtained:

whereais the drive voltage.

Fig. 4 shows the system's resonant amplitude under no-load and loaded conditions for different compensation capacitances, which are obtained through Eq. (14). Under no-load conditions, the resonance amp litude of the system first increases and then decreases with the compensation capacitance. The resonance amplitude reaches its maximum value under the optimal compensation capacitance. When the system is under load, the no-load optimal compensation capacitance can still achieve the maximum amplitude and maintain the best machining performance. In summary, the optimal compensation capacitance is still adequate for the operation of GMUPS under load.

3 Experimental verification

A series of experiments was conducted under no-load and loaded conditions to evaluate the validity of the optimal compensation capacitance model. Firstly, the parameters of the transducer were identified to calculate the theoretical value of the optimal compensation capacitance. Then, idle vibration measurement tests for different compensation capacitances were carried out to verify the developed model under no-load condition. Finally, drilling experiments were performed to evaluate the performance of the optimal compensation capacitance under loaded condition.

Fig. 4 Idle resonance frequency amplitude curve of the system with different compensation capacitance (a) and resonance amplitude with different compensation capacitance under load (b)

3.1 Obtaining optimal compensation capacitance

To calculate the optimal compensation capacitance, it is necessary to obtain the required parameters through measurements, including the basic electrical parameters of the GMUPS, the mechanical resonance frequency, and the other variables included in Eq. (11), such asemand. The parameter identification experiments of the transducer were conducted on a self-designed GMUPS, which is mounted on a computerized numerical control (CNC) lathe (DMG CTX310, DMG, Germany). The experimental platform is shown in Fig. 5. The basic electrical parameters of GMUPS with LCCPT were measured by a multimeter with results listed in Table 1.

The mechanical resonance frequencies of GMUPS, with and without LCCPT, can be derived from the amplitude-frequency curves of the system, which were measured using a laser displacement sensor (LK-H008, Keyence, Japan) with a sampling rate of 392 kHz with a revolution of 0.01 μm. The measurement results of amplitude-frequency curves are shown in Fig. 6. The mechanical resonance frequencies are 19640 Hz in both cases with and without LCCPT. However, after using LCCPT, the system's electrical circuit has changed significantly, which induces a distinct electrical resonance frequency compared with the system without LCCPT. Therefore, although there is a coupling between the mechanical and electrical parts of the system, the mechanical resonance frequency and the electrical resonance frequency are independent. Thus, mechanical and electrical resonances can be considered separately in the study of ultrasonic systems.

Fig. 5 Experimental setup of displacement measurement: (a) process and measurement part; (b) control part

Table 1 Basic parameters of GMUPS

Fig. 6 Amplitude-frequency curve of GMUPS with and without LCCPT

According to Eq. (11),emandare also needed to calculate the optimal compensation capacitance and can be obtained by measuring the impedance circle when the LCCPT is not used. However, calculatingemandby measuring the impedance circle needs a large amount of data to fit the impedance circle; the calculation process is very complicated. So other, less complicated approaches are needed and are described as follows.

We combine the impedance of the excitation coil with the equivalent impedance of the transducer obta ined by the first equivalent circuit mapping (Fig. 3b) as

wheremsis the equivalent resistance of the system when the LCCPT is not used,cis the reactance of the excitation coil, andmsis the equivalent reactance of the system when the LCCPT is not used.

Substituting Eqs. (7) and (15) into Eq. (11) and simplifying, the optimal compensation capacitance can be expressed as follows:

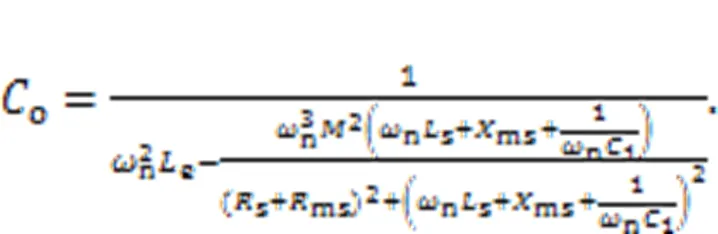
According to Eq. (16), the optimal compensation capacitance can be calculated after obtaining1,ms, andms.msandmscan be obtained by measuring the mechanical resonant current and the mechanical resonant voltage through the power meter (PW3335, HIOKI, Japan) when the LCCPT is not used. According to Eq. (15) and Figs. 2a and 3,1is only an intermediate variable when calculatingo. Different values of1will changems, but will not changeoando. Theoretically, therefore,1does not affecto.

虽然我国正在逐步加强城市化建设力度，但是当前乡镇数量众多，故设计合理的固体废弃物处理方式时仍然要以该类对象角度考虑。水泥窑系统处置废弃物量约为100t/d，处理垃圾种类多为热值较高的生活垃圾、污泥、餐余废物乃至危险废物等，且建设面积小、所需投资金额较低、所用设备无需转运或长途运输，对乡镇地区较为友好，便于投入正式使用。

However, we can use1to calculateomore accurately by carrying out experiments at different values of1. Experiments were conducted at different1of 50, 60, 65, 70, 75, 80, 90, and 100 nF using the PW3335 power meter and power supply (BP4610, NF, Japan). The measurement results ofmsandmsare listed in Table 2. By substitutingmsandmsinto Eq. (13), the optimal compensation capacitanceois calculated with the results listed in Table 2. It should be noted that1does not exist in the final actual circuit, and it is only used in the process of solvingo. Taking the average value ofoin Table 2, the optimal compensation capacitance is obtained as 46.10 nF.

Table 2 Theoretical value of Co

3.2 Performance of optimal compensation capacitance without load

The performance of the GMUPS with the optimal compensation capacitance under no-load conditions was evaluated using the device shown in Fig. 5. Firstly, the amplitude-frequency curves under different compensation capacitances of 40, 45, 48, and 51 nF were measured with results shown in Fig. 7a. The maximum amplitude under all compensation capacitance is around 19640 Hz, and does not change with the compensation capacitance. This phenomenon further illustrates that the electrical and mechanical properties of the system are independent of each other. Therefore, the relationship curve between resonance amplitude and compensation capacitance can be measured at 19640 Hz to obtain the optimal value of compensation capacitance. The measurement results are shown in Fig. 7b.

Fig. 7 Amplitude-frequency curve of different compensation capacitances (a) and relationship curve between resonance amplitude and compensation capacitance (b)

The GMUPS with optimal compensation capacitance shows much-improved resonance performance for no-load conditions. The shape of the resonance amplitude-compensation capacitance curve has a high similarity to the theoretical curve (Fig. 4a). The resonance amplitude first increases and then decreases with the compensation capacitance. The resonance amplitude reaches its maximum value of 10.9 μm around the theoretical value of optimal compensation capacitance of 46.1 nF. These experimental results verify the efficacy of the developed model of optimal compensation capacitance.

The GMUPS can work at both mechanical and electrical resonances simultaneously when the optimal compensation capacitance is utilized. The amplitude-frequency and phase-frequency curves were measured with results shown in Fig. 8. As demonstrated in Fig. 8, the frequency corresponding to the zero-phase point coincides with the frequency of maximum amplitude. Thus, the electrical resonance and mechanical resonance co-occur. In this circumstance, the system works with maximum energy utilization efficiency. It should be noted that in the resonance experiment, the phase response of the system reaches zero at several driving frequencies. However, the ultrasonic system can achieve the maximum vibration amplitude at only one of the zero-phase frequencies (Jiang and Zhang, 2007).

Fig. 8 Results of the resonance experiment with optimal compensation capacitance

Fig. 9 Drilling platform (a) and cutting force variation during drilling with the compensation of 46.1 nF (b)

3.3 Performance of optimal compensation capacitance during drilling

A series of drilling experiments was performed to verify the effectiveness of the optimal compensation capacitance under load. The experimental setup is shown in Fig. 9. The GMUPS with LCCPT is fixed using a three-jaw chuck to achieve the rotary motion. The workpiece is fixed on the tool holder to provide the feeding motion. The workpiece material is quartz ceramic. The drilling experiment uses a carbide tool with a diameter of 6 mm. It is electroplated with diamond abrasive grains with mesh size of 120/140. The spindle speed of 3000 r/min and the feed rate of 5 mm/min were used for drilling experiments. A dynamometer (9256C2, Kistler, Switzerland) was used to measure the cutting force during the drilling process with a sampling rate of 1000 Hz.

Fig. 9b shows the variation of cutting force for a complete drilling process. Since this experiment uses an external cutting fluid, it becomes more difficult for the cutting fluid to work as the drilling depth increases, and thus the cutting force increases with the drilling depth. Therefore, when discussing the compensation effect of different compensation capacitances, it is sufficient to compare the cutting force at the beginning stage and the finishing stage. It can be obtained from Fig. 7b that the compensation capacitances corresponding to the half-power points are 40.7 and 52.5 nF. Thus, two points around the half-power band are selected as controls. The compensation capacitances of 0, 41.0, 46.1, 51.0, and 100.0 nF were used for drilling experiments, with results shown in Fig. 10.

The GMUPS with optimal compensation capacitance also works well during machining. Fig. 10 shows the cutting force at the beginning and finishing stages using the GMUPS with different compensation capacitances. Under the optimal compensation capacitance (46.1 nF), the cutting forces for both the beginning and finishing stages reach the smallest values. It is well recognized that the cutting force decreases with the ultrasonic amplitude in RUM (Wang et al., 2020). Thus, in Fig. 10, a smaller cutting force indicates a larger ultrasonic amplitude, which is consistent with the variation trend of resonant amplitude in Fig. 7. The experimental results are in accordance with the theoretical analysis in Section 2.5 and demonstrate that the capacitance compensation method is effective not only under no-load but also under load.

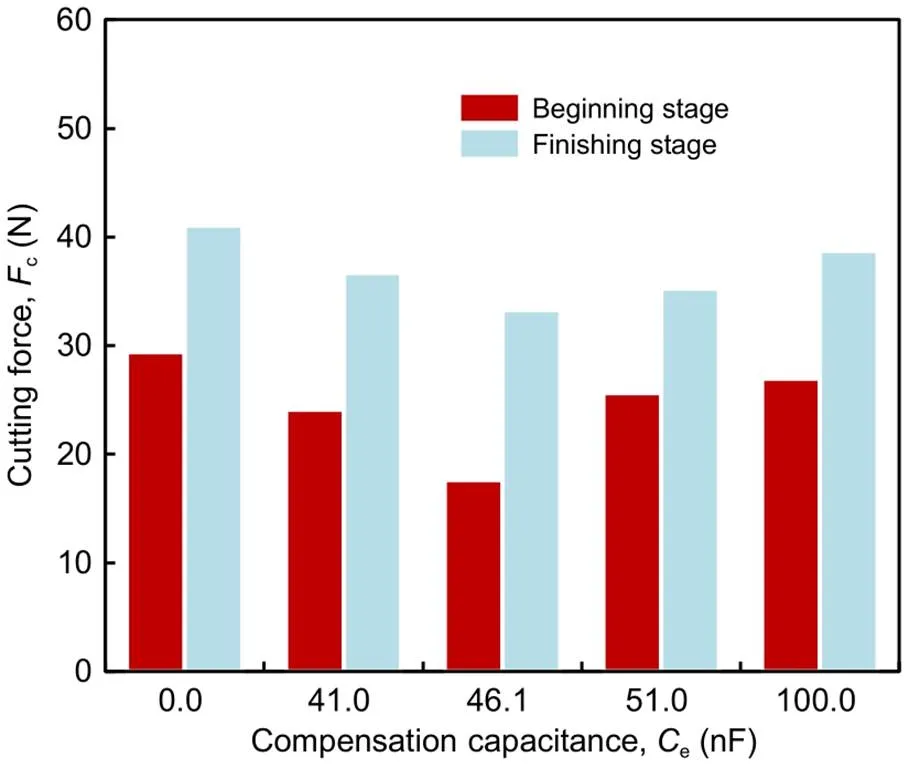
Fig. 10 Results of the drilling experiments

4 Effect factors of the phase lag angle

The optimal compensation capacitance is directly related to the phase lag angle, as shown in Eq. (11). The phase lag angle greatly affects the performance of GMUPS. To study the effect factors of the phase lag angle, it is first necessary to obtain the equation of the phase lag angle. Substituting Eqs. (1), (2), and (5) into Eq. (16) and simplifying,can be obtained by solving Eq. (17) as follows:

According to Eq. (17),can be calculated after obtainingemandem.emandemcan be obtained by measuringms,ms, and the equivalent electrical parameters of GMUPS. It is worth noting that the change of the mechanical resonance frequency under different driving voltages is only tens of Hertz, which is very small compared to the resonance frequency. Thus, 19640 Hz is set as the resonance frequency. Other equivalent circuit parameters of the GMUPS system can be measured by the impedance analyzer (PV70A, Beijing Banglian, China), and the results are shown in Table 3. After getting these parameters, experiments to explore the effect of driving voltages and magnetic material on the phase lag angle are performed by measuringmsandms, since they are critical factors that affect the system's idle vibration amplitude.

4.1 Driving voltage

Table 3 Equivalent parameters of GMUPS

Fig. 11 Phase lag angle with different driving voltage (a) and phase lag angle with different materials (b)

4.2 Material of the magnetic conductive structure

To ensure the closed loop of the internal magnetic circuit of the transducer, a magnetic conductive structure is arranged inside the transducer. Different materials have different core losses and skin effects, resulting in different phase lag angles. The phase lag angle and the frequency difference (Δ) between the mechanical resonance frequency and the minimum current frequency were measured using magnetic powder and ingot iron as magnetic conductive structure materials, respectively. The measurement results are shown in Fig. 11b.

The GMUPS using a magnetic powder core achi eves a smaller phase lag angle and less difference between the mechanical resonance frequency and the minimum current frequency. This is because the magnetic powder core material is sintered compared with the ingot iron material. As a result, its iron loss and skin effect are weaker, resulting in less unnecessary energy loss. Thus, the phase lag angle and frequency deviation of GMUPS using the magnetic powder core are smaller than those of ferromagnetic materials. Therefore, we recommend that the magnetic powder core is used as the magnetic conductive material for GMUPS.

5 Conclusions

In this study, the model of optimal compensation capacitance for GMTs with an LCCPT is developed to achieve the maximum energy utilization efficiency. The model stresses the phase lag angle between the mechanical and electrical circuits, while considering the non-negligible loss in energy conversion caused by the core loss and the skin effect in GMM. Idle vibration experiments and machining tests are conducted to verify the developed model. The following conclusions are drawn:

1. The adoption of optimal compensation capacitance shows superior performance for both idle and machining conditions. The system can obtain the maximum amplitude and achieve the highest energy efficiency, while the cutting force is the smallest in the whole process of machining when the optimal compensation capacitance is adopted.

2. The use of LCCPT and the value of the compensation capacitance significantly affect the electrical characteristics of the system but have only a slight effect on the mechanical resonance frequency. Thus, the electrical resonance frequency of the system can be changed independently by the compensation capacitance. The system's performance can be improved by making the electrical resonance frequency closer to the mechanical resonance frequency.

3. The phase lag angle between the electrical circuit and the equivalent mechanical circuit of the system results in a discrepancy between the minimum current frequency and the mechanical resonance frequency. The phase lag angle is directly related to the unnecessary power loss of the system. The driving voltage has little effect on the phase lag angle before reaching magnetic saturation. However, the material properties of the magnetic conductive structure, such as core loss, notably affect the phase lag angle. Therefore, selecting the magnetic conductive material with low loss at high frequency can effectively reduce the phase lag angle.

This work is supported by the National Natural Science Foundation of China (Nos. 51875311 and 52105458), the Tsinghua-Foshan Innovation Special Fund (No. 2021THFS0204), and the Huaneng Group Science and Technology Research Project (No. HNKJ22-U22YYJC08), China.

Tian LAN made the theoretical derivation and experimental design and processed the corresponding data. Hui-lin ZHOU participated in the theoretical model design. Jian-fu ZHANG helped to make the experiment. Jian-jian WANG wrote the first draft of the manuscript. Ping-fa FENG revised and edited the final version.

Tian LAN, Ping-fa FENG, Jian-jian WANG, Jian-fu ZHANG, and Hui-lin ZHOU declare that they have no conflict of interest.

Cai WC, Zhang JF, Feng PF, et al., 2017a. A bilateral capacitance compensation method for giant magnetostriction ultrasonic processing system., 90(9):2925-2933. https://doi.org/10.1007/s00170-016-9602-4

Cai WC, Zhang JF, Yu DW, et al., 2017b. Research on the electromechanical conversion efficiency for giant magnetostrictive ultrasonic machining system., 53(19):52-58 (in Chinese). https://doi.org/10.3901/JME.2017.19.052

Calkins FT, 1997. Design, Analysis, and Modeling of Giant Magnetostrictuve Transducers. PhD Thesis, Iowa State University, Ames, USA.

Chen L, Zhu YC, Yang XL, et al., 2014. Driving magnetic path modeling and numerical analyses in giant magnetostrictive pump., 25(6):718-722 (in Chinese). https://doi.org/10.3969/j.issn.1004-132X.2014.06.002

Chen WY, 2015. Research on Underwater Acoustic Transducer Based on Giant Magnetostrictive Material. MS Thesis, Hangzhou Dianzi University, Hangzhou, China(in Chinese).

Claeyssen F, Lhermet N, Le Letty R, et al., 1997. Actuators, transducers and motors based on giant magnetostrictive materials., 258(1-2):61-73. https://doi.org/10.1016/S0925-8388(97)00070-4

Fan P, Feng PF, Zhang JF, et al., 2019. Design and compensation of partially coupled contactless power transmission in GMM ultrasonic processing system., 62(5):88-95 (in Chinese). https://doi.org/10.16080/j.issn1671-833x.2019.05.088

Gong H, Fang FZ, Hu XT, 2010. Kinematic view of tool life in rotary ultrasonic side milling of hard and brittle materials., 50(3):303-307. https://doi.org/10.1016/j.ijmachtools.2009.12.006

Huang HY, Paramo D, 2011. Broadband electrical impedance matching for piezoelectric ultrasound transducers., 58(12):2699-2707. https://doi.org/10.1109/TUFFC.2011.2132

Jiang XG, Zhang DY, 2007. Matching theory of ultrasonic transducer at its passed inherent resonance zone., 43(3):‍182-186 (in Chinese). https://doi.org/10.3321/j.issn:0577-6686.2007.03.031

Liu DF, Cong WL, Pei ZJ, et al., 2012. A cutting force model for rotary ultrasonic machining of brittle materials., 52(1):77-84. https://doi.org/10.1016/j.ijmachtools.2011.09.006

Liu JJ, Jiang XG, Gao Z, et al., 2019. Investigation of the effect of vibration amplitude on the surface integrity in high-speed rotary ultrasonic elliptical machining for side milling of Ti-6Al-4V., 55(11):215-223 (in Chinese). https://doi.org/10.3901/JME.2019.11.215

Ma K, Wang JJ, Zhang JF, et al., 2022. A highly temperature-stable and complete-resonance rotary giant magnetostrictive ultrasonic system., 214:106927. https://doi.org/10.1016/j.ijmecsci.2021.106927

Pang MX, 2010. The Design Theory and Experimental Study of Non-contact Ultrasonic Power Transfer Device. MS Thesis, Taiyuan University of Technology, Taiyuan, China (in Chinese).

Shen H, Feng PF, Zhang JF, et al., 2015. Circuit compensation for efficient contactless power transmission in ultrasonic vibration systems., 55(7):728-733 (in Chinese). https://doi.org/10.16511/j.cnki.qhdxxb.2015.07.004

Song Z, Li YJ, Zhang CG, et al., 2019. Rotating core loss model for motor considering skin effect and dynamic hysteresis effect., 35(6):74-80. https://doi.org/10.11975/j.issn.1002-6819.2019.06.009

Wakiwaka H, Lio M, Nagumo M, et al., 1992. Impedance analysis of acoustic vibration element using giant magnetorestrictive material., 28(5):2208-2210. https://doi.org/10.1109/20.179445

Wang H, Pei ZJ, Cong WL, 2020. A feeding-directional cutting force model for end surface grinding of CFRP composites using rotary ultrasonic machining with elliptical ultrasonic vibration., 152:103540. https://doi.org/10.1016/j.ijmachtools.2020.103540

Wang JJ, Zhang CL, Feng PF, et al., 2016. A model for prediction of subsurface damage in rotary ultrasonic face milling of optical K9 glass., 83(1-4):347-355. https://doi.org/10.1007/s00170-015-7567-3

Wang JJ, Wang YK, Zhang JF, et al., 2021. Structural coloration of non-metallic surfaces using ductile-regime vibration-assisted ultraprecision texturing., 2(4):434-445. https://doi.org/10.37188/lam.2021.033

Wang XQ, Feng DR, Shang L, et al., 2004. Measurement and analysis of the pulsed magnetic field phase lag in the ceramic case., 53(12):4319-4324 (in Chinese). https://doi.org/10.3321/j.issn:1000-3290.2004.12.049

Wang Y, Lin B, Wang SL, et al., 2014. Study on the system matching of ultrasonic vibration assisted grinding for hard and brittle materials processing., 77:66-73. https://doi.org/10.1016/j.ijmachtools.2013.11.003

Zeng GX, 2013. Theoretical Analysis and Experimental Study of the Giant Magnetostrictive Power Ultrasonic Transducer. PhD Thesis, South China University of Technology, Guangzhou, China (in Chinese).

Zhang JG, 2019. Research on Compensation Optimization of Wireless Power Transmission and Control System of Rotary Ultrasonic Machining. PhD Thesis, Harbin Institute of Technology, Harbin, China (in Chinese). https://doi.org/10.27061/d.cnki.ghgdu.2019.005041

Zhang TL, Jiang CB, Zhang H, et al., 2004. Giant magnetostrictive actuators for active vibration control., 13(3):473-477. https://doi.org/10.1088/0964-1726/13/3/004

Zhou HL, Zhang JF, Feng PF, et al., 2019. An output amplitude model of a giant magnetostrictive rotary ultrasonic machining system considering load effect., 60:340-347. https://doi.org/10.1016/j.precisioneng.2019.07.005

Zhou HL, Zhang JF, Feng PF, et al., 2020a. An amplitude prediction model for a giant magnetostrictive ultrasonic transducer., 108:106017. https://doi.org/10.1016/j.ultras.2019.106017

Zhou HL, Zhang JF, Feng PF, et al., 2020b. On the optimum resonance of giant magnetostrictive ultrasonic transducer with capacitance-based impedance compensation., 29(10):105002. https://doi.org/10.1088/1361-665X/ab9f4d

Zhou HL, Zhang JF, Feng PF, et al., 2021. Investigations on a mathematical model for optimum impedance compensation of a giant magnetostrictive ultrasonic transducer and its resonance characteristics., 110:106286. https://doi.org/10.1016/j.ultras.2020.106286

July 27, 2022;

Revision accepted Aug. 23, 2022;

Crosschecked Sept. 23, 2022

© Zhejiang University Press 2022