Hydrodynamics of high-speed robots driven by the combustion-enabled transient driving method

Yang YANG, Yingzhong LOU, Guanzheng LIN, Zhiguo HE1,,4, Pengcheng JIAO1,,4

Research Article

Hydrodynamics of high-speed robots driven by the combustion-enabled transient driving method

1Hainan Institute, Zhejiang University, Sanya 572000, China2Institute of Port, Coastal and Offshore Engineering, Ocean College, Zhejiang University, Zhoushan 316021, China3Department of Civil and Environmental Engineering, University of Washington, Seattle, WA 98195, USA4Engineering Research Center of Oceanic Sensing Technology and Equipment of Ministry of Education, Zhejiang University, Zhoushan 316021, China5Department of Electronic Engineering, Faculty of Engineering, The Chinese University of Hong Kong, Hong Kong 999077, China

Underwater vehicles play important roles in underwater observation, ocean resource exploration, and sample collection. Soft robots are a unique type of underwater vehicles due to their good environmental adaptability and motion flexibility, although they are weak in terms of actuation and response ability. The transient driving method (TDM) was developed to resolve these shortcomings. However, the interaction between the robots’ swift motions and flow fields has not yet been fully studied. In this study, a computational fluid dynamic model is developed to simulate the fluid fields disturbed by transient high-speed motions generated by the robots. Focusing on the dependence of robot dynamics on thrust force and eccentricity, typical structures of both flow and turbulence fields around the robots are obtained to quantitatively analyze robot kinematic performance, velocity distribution, vortex systems, surface pressure, and turbulence. The results demonstrate the high-speed regions at the robots’ heads and tails and the vortex systems due to sudden expansion, indicating a negative relationship between the maximum fluid velocity and eccentricity. The reported results provide useful information for studying the environmental interaction abilities of robots during operating acceleration and steering tasks.

Underwater vehicle; Computational fluid dynamics (CFD); Robotics; Transient driving method (TDM); Combustion actuation; Hydrodynamics

1 Introduction

Underwater vehicles are of importance in ocean engineering for activities such as underwater observation, marine resource exploration, sample collection, and health monitoring of underwater structures (Trivedi et al., 2008; Majidi et al., 2013; Lee et al., 2017; Bai et al., 2022). Underwater soft robots are unique vehicles which perform better than rigid robots due to their satisfactory environmental adaptability and kinematic flexibility (Umedachi et al., 2013; Rus and Tolley, 2015; Li TF et al., 2016; Calisti et al., 2017). When it comes to specific application scenarios in underwater environments, the robots can adapt to operating conditions and perform motions in a way that generates less disturbance to the fluid field (Villanueva et al., 2011; Chu et al., 2012; Suzumori et al., 2017). Their interactions with fluids are well studied (Grissom et al., 2006; Wiguna et al., 2006; Najem et al., 2012). Benefiting from soft smart materials, an underwater soft robot can perform various functional motions in response to different stimuli. For example, a dielectric elastomer-actuated soft fish was able to swim in the Mariana Trench by flapping its wings in response to electronic stimuli (Li et al., 2021). Shape-memory materials were also demonstrated to respond to temperature stimuli to actuate a frog-inspired underwater soft robot (Soomro et al., 2021). In another study, a nano-scale soft robot was actuated to deliver drugs in the water environment in response to PH stimuli (Li H et al., 2016). Nevertheless, due to the lack of actuation power generated by soft materials, the underwater soft robots in the literature typically have difficulty in accelerating to high speeds in the short actuation period. Significant tasks such as underwater high-speed start-up, rapid underwater obstacle avoidance, or fast steering are urgently needed, but they are not easily attained with the typical underwater soft actuation methods due to the relatively low actuation power density. Therefore, the combustion-actuated underwater soft robot was proposed to resolve the dilemma. The transient driving method (TDM) was developed to use combustion to address the challenge (Yang et al., 2020). Combustion can immediately generate high hydro-pressure, which deforms soft robots' flexible components for high-speed actuation. Combustion-enabled TDM was first reported by Shepherd et al. (2013), which designed on-land jumpers that exhibited powerful thrust forces in their motions. The combustion-powered hydro-jet engine (CPHJE) also equipped cephalopod-inspired jetters for underwater transient high-speed motions (Keithly et al., 2018). In addition to straight motions, controllable motions have been attempted with the TDM by pre-changing the head orientation (Bartlett et al., 2015) and landing point (Loepfe et al., 2015). Quantitative assessments were conducted on the driving ability of TDM-enabled actuators (Yang et al., 2020), and the research team designed the actuators into underwater jumpers to obtain approximately three-time-body-length jumping.

The fluid field also critically affects underwater movements, and can be used to optimize the design of the robots and the solid-fluid interactions (Chen et al., 2007; Tang et al., 2009; Wang et al., 2019). Additionally, in terms of ocean engineering, studying the environment (i.‍e., fluid fields) when disturbed by vehicular motions is significant. Therefore, numerical simulations using the computational fluid dynamics (CFD) method were carried out to obtain hydrodynamic coefficients of a robot tuna for high-accuracy motion prediction (Wang et al., 2019). Numerical analysis was also developed based on the bionic robot tuna using the CFD method, to investigate the surface pressure, turbulent kinetic energy, fluid velocity, and other flow performance indicators in relation to the robot tuna (Chen et al., 2007). Drag forces were fully studied by developing a numerical model of an autonomous underwater vehicle (AUV) (Lin et al., 2022). Movements and deformations of an underwater shell-like robot were also studied by the CFD method to accurately assess its motion strategies (Renda et al., 2015).

However, the fluid field impacted by TDM robots is still not completely understood due to the complex motions and the high Reynolds fluid environments generated by combustions that occur within about 20 ms. The interaction between robots and the fluid field around them during operating acceleration and steering tasks must be thoroughly studied. Thus, in this work, a coupling CFD model was developed to study the fluid fields disturbed by the TDM underwater motions. We numerically studied the fluid field disturbed by robots driven by TDM to obtain the hydrodynamic characteristics and interaction processes. This paper is organized as follows: Section 2 presents the numerical setup and the calibration of the thrust forces acting on the underwater robots, which enable the robots to perform straight swimming or tunable steering. Section 3 presents the numerical results, including the robots' kinematic performance, hydro-velocity distribution, hydro-pressure distribution, and turbulence kinematic energy distribution. Section 4 presents the conclusions of this study.

2 Methods

The numerical model was developed using a CFD model based on ANSYS Fluent (Lou et al., 2019). The main governing equations (i.e., Reynolds-averaged Navier-Stokes equations) and the details of the numerical methods are provided in Sections S1 and S2 of the electronic supplementary materials (ESM). The calculational domain of the model is a cuboid (where the side lengthis 600 mm, and the heightFis 1175 mm ) which is surrounded by a wall and has a pressure outlet above it. The robots are located in the center of thecoordinate plane, and1=75 mm is the distance between the robots and the bottom. Because the internal electrical components and pneumatic equipment of the real model are relatively complex, a simplified model of the robots was established to ensure the similarity of hydrodynamic characteristics, as shown in Fig. 1. The soft actuator applied in the robot was previously studied, and the shape of the model, including a hemispherical head (radiusH=75 mm) and a cylindrical body (heightR=200 mm), is similar to the real model in all directions, thus leaving the projection area unchanged. It should be noted that this combination cylinder/hemisphere soft robot actuated by combustion has been successfully applied to achieve an underwater rapid start-up (Keithly et al., 2018), leaps out of the water (Yang et al., 2020), and multi-environment signal transmission (He et al., 2022).

Fig. 1 Setup for the numerical simulation of a fluid field disturbed by robots driven by combustion, including the system coupling, the dynamic mesh, and the design principle of the robots. t is the time

This computational domain is completely divided into tetrahedral cells. Specifically, the area occupied by the robots is divided into nearly 2×105tetrahedral cells with a size of 1 mm, and the area of the whole flow field is divided into 9×105tetrahedral cells with a size of 33.3 mm, as shown in Table 1. Fig. 1 shows the mesh reconstruction for the combustion driving process of the robots. To obtain the actuator's thrust-time relationship for the chemical combustion reaction, we mixed oxygen (O2) and propane (C3H8) to obtain combustion gas, which was fully mixed into the actuator. We put loads with different masses onto an actuator sealed with a soft membrane, and input different volumes of the premixed gas. By igniting the gas, combustions quickly increased the pressure of the chamber, resulting in large deformations of the membranes and also pushing the mass upward. A high-speed optical camera with 12000 frame/s was used to capture the transient driving process of the push plate driven by the actuator. After binary processing of image information, we found that the transient driving process of the actuator began with the membrane overcoming the gravity of the push plate and providing significant thrust in the period of 0.0‍–8.7 ms. After=8.7 ms, the plate and the membrane were in the contact limit state. After that, because of inertia, the plate continued to move upward. Therefore, we changed the load of the plateand the total amount of gas, and selected the displacement-time data of the plate before 8.7 ms to create the displacement-time image shown in Fig. 2a. Then we calculated the second derivative of the displacement, and combined it with Newton's second law to obtain the relationship between thrust force and time, as shown in Fig. 2b and Table 2 (see detailed measurement setup in Section S4 of the ESM). After fitting the thrust-time relationship of Fig. 2b, it was evident that the relationship wasT=cos(180) under different working conditions (Tis the thrust force, and the value of the maximum thrustis shown in Table 2); this was consistent with previous study (Wang et al., 2021).

Table 1 Dimensions of the simulated fluid field

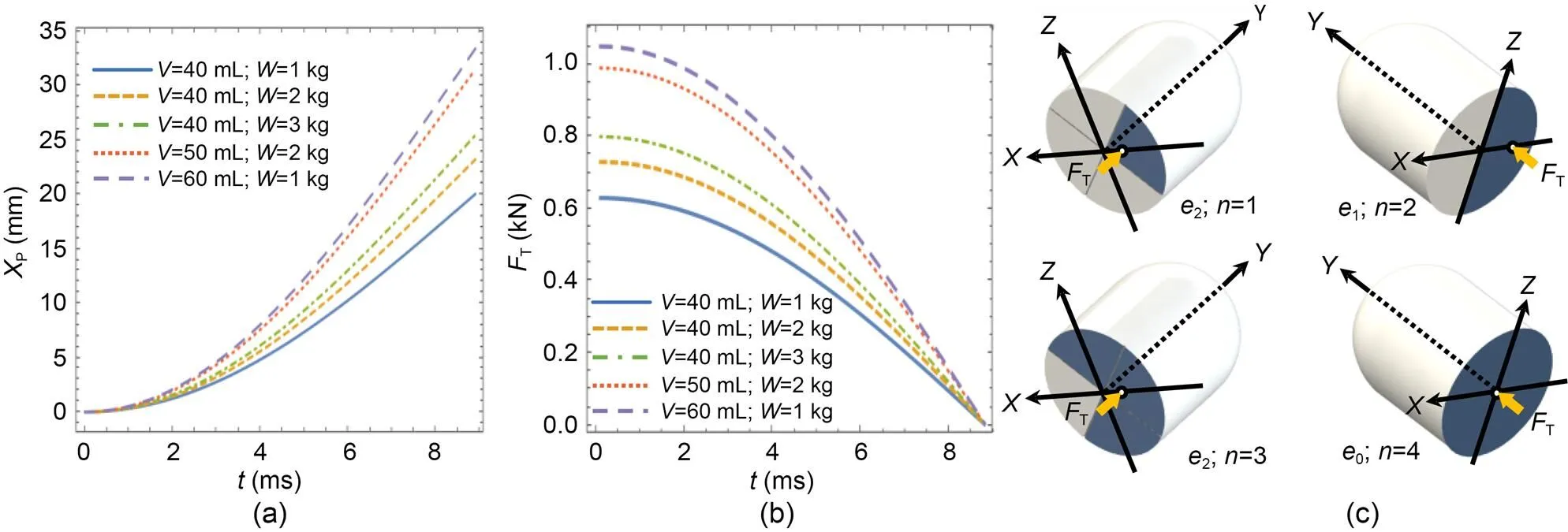
Fig. 2 Calibration of the thrust force generated by combustion: (a) relationships between displacement of the push panel XP and time, obtained from the calibration experiments; (b) relationships between thrust force and time, processed from (a); (c) illustration of the applied thrust force in the numerical simulations

Table 2 Experimental results of thrust calibration

This study employed the standard-‍model (wheredenotes the turbulent kinetic energy, anddenotes the turbulence dissipation rate) (Launder and Spalding, 1974) for the closure of the Reynolds equations (see Section S1 of the ESM for detail). The robustness and accuracy of the-model have been extensively verified through many simulations; its high stability and efficiency made it feasible to model the high-Reynolds-number turbulence induced by the TDM of the robots. The time step of 0.0005 s was selected to ensure that the numerical calculation could be converged within 20 iterations at each time step. For each case, we took the simulation results before 0.1000 s for analysis, in order to focus on the combustion actuation process which took place in the period before 0.0089 s.

3 Results and discussion

3.1 Kinematic result

Because theplane bisects the acting region of thrust force underneath the robots, we chose it to analyze the underwater robots' numerical simulation results. The acting region of the thrust force is located on the right side of theplane. Based on the numerical results, the robots' whole single steering motion can be divided into two types of movements: displacement (comprising the acceleration and deceleration processes) and self-rotation. Fig. 3 shows the directional displacements of the robots. It should be noted that the motions of cases 1, 4, 7, 10, and 13 were straight motions, and were therefore excluded. The eccentricity of cases 2, 5, 8, 11, and 14 was1, and that of cases 3, 6, 9, 12, and 15 was2. It can be seen that, with high thrust forces generated by combustion, the robots in every sub-figure in Fig. 3 showed an obvious acceleration process (during 0–10 ms). These results demonstrate high actuation performance and thus confirm the unique advantage of the TDM; they suggest that because of the rapid transformation of combustion energy to kinetic energy, the robot's deceleration process starting at about 10 ms is one of the most important parts of the overall motion. It is noteworthy that a curve intersection shown in the-direction distribution with2is due to the over-rapid self-rotation of the robots. Fig. 4 shows the final angles (at=100 ms) of the self-rotation with different eccentricities and calibrated thrust forces. The robots driven by TDM can rotate about 5 rad on average, and at most about 6 rad, in 100 ms. With incremental increases in eccentricity, the robots' final angles also increased, and the increasing thrust forces overall led the final angles to change in the same pattern. However, it should be noted that the final angles of self-rotation reached their maximum at4, which is due to the high kinematic energy consumption required to overcome displacement drag and rotational drag.

Table 3 Summary of parameters for the numerical simulations

Fig. 3 Relationships between directional displacements (X and Y) and time for different cases. The arrows indicate the developing trends

Fig. 4 Density plot of the final angle (t=100 ms) with different eccentricities and calibrated thrust force conditions

3.2 Velocity distribution

Focusing on the dependence of robot dynamics on eccentricity, we analyzed the velocity fields on theplane for cases 4‍–‍6. The model results, as shown in Fig. 5, suggest considerable shared characteristics between the flow fields surrounding the robots with different eccentricities. Specifically, in all these cases, the flow velocity will attain the local maximum values in the robots' heads and tails during the acceleration stage (the first 8.7 ms of the overall motion). This spatial characteristic will hold during the deceleration stage (i.‍e., from 0.01 to 0.10 s), at which point the thrust force on the robot has ceased. Meanwhile, the significant impacts of eccentricity on the fluid field are evident in the results. When the thrust force acts uniformly on the bottom of the robots, i.e., the eccentricity of the robots is 0 and thus leads to symmetrical velocity distribution around the robots, it is worth noting that there are considerable vortices induced by the shear stress between the robots and the surrounding fluids at=0.01 s. Both the shear strain rate and the vortex energy on both sides of the robot will gradually decrease during the deceleration stage due to the decrease of the velocity gradient around the robots. In comparison, an asymmetrical thrust force may lead to complex fluid fields, as suggested by the results for cases 5 (1=0.424) and 6 (2=0.600). In such circumstances, the robots' deflection angles will increase with time, and the high-speed region of fluid will gradually transfer to the side of higher thrust force. A vortex, meanwhile, may form at the bottom right-hand corner of the robots due to the fast rotation there. Furthermore, the model results suggest that the velocity magnitude of the fluid surrounding the robots will generally decrease with increasing eccentricity, while the high-speed region at the tail of the robots will move to the right side more quickly. Simultaneously, the vortex structure located under the robots will transfer to the side of the higher thrust force corner because the deflection of the corner on that side of the robots has a greater shear effect on the surrounding fluids.

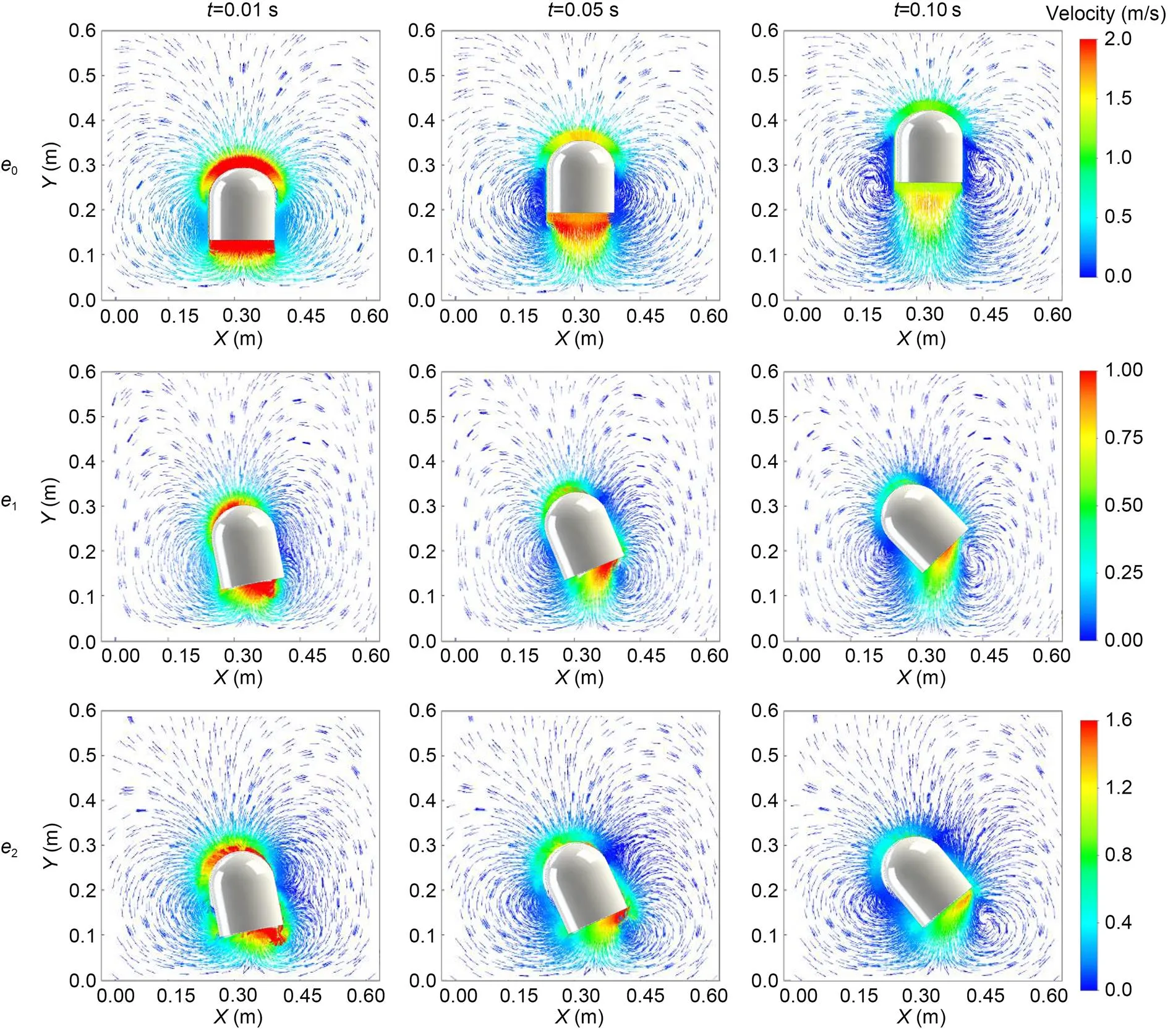
Fig. 5 Velocity distributions of cases 4–6 at t=0.01, 0.05, and 0.10 s

3.3 Pressure distribution

Fig. 6 shows the pressure distribution results from the numerical simulations. Cases 1–3 and 10–15 were selected to study the pressure distribution on robots' surfaces in different thrust and eccentricity scenarios. The results for cases with zero eccentricity (i.‍e., cases 1, 10, and 13) suggest that high-pressure and low-pressure areas can be respectively observed at the robots' heads and tails due to the boundary layer effects. As expected, the magnitude of pressure anomalies will increase with increased thrust force. The results for cases 2, 3, 11, 12, 14, and 15 show that when the force is asymmetrical (i.e.,≠0), the deflection of the robot increases with increased force, leading to a high-pressure area on the side of the robots with higher thrust force and a low-pressure area on the side with lower thrust force. The maximum/minimum values of the positive/negative pressure anomalies on robot surfaces decrease along with the eccentricity.

Fig. 6 Pressure distributions of cases 1–3 and 10–15 at t=0.1 s

Meanwhile, the high-pressure areas on the top and left of the robots shift to the right; the low-pressure area on the left disappears gradually, and that on the bottom moves upward. Fig. 7 describes the influence of different thrust forces and eccentricities on the robot surfaces' maximum pressures. The maximum pressure variations with time show that the maximum pressure on the robot surfaces has a positive relationship with thrust force and a negative relationship with eccentricity. Moreover, it appears that the maximum pressure on robot surfaces will increase rapidly in the acceleration stage (i.‍e.,<8.7 ms). The robots will then enter the deceleration stage because of losing thrust force, and the pressure gradient on surfaces will decrease gradually.

3.4 Turbulence structure

Turbulence induced by robot motions can be characterized by the turbulent kinetic energy () and turbulence dissipation rate (). As shown in Fig. 8, the model results suggest remarkable differences in the distribution ofamong different motion stages. When eccentricity is zero, turbulent kinetic energy attains its local maximum values at the head and two corners of the tail during the acceleration stage, indicating the significant turbulence induced by the high-pressure region and boundary layer separation, respectively. During the deceleration stage, the high-regions at the robots' tails will gradually transfer from the corners to the wake due to shear flows. Meanwhile, the maximum local value can still be reached at the head, consistent with the available observations (Hamed et al., 2017; Yagmur et al., 2020). It should be noted that during the deceleration stage, low-regions can be observed on both sides of the robot's body, which implies that the viscosity due to the solid boundary may suppress the turbulence in the near-wall regions and thus make the boundary layer flow more like laminar flow. When the thrust force is asymmetrical, the tails' high-regions are prone to transfer to the side with a higher thrust force during the acceleration stage. The strong turbulence by the head, at the same time, will be weakened, since the considerable rotation here may moderate the fluid compression, although such rotation itself may increase turbulence, as suggested by the results for case 6.

The distributions ofamong different motion stages (Fig. 9) demonstrate a similar tendency to those of. The model results suggest thatwill attain its local maximum values at the two corners of the tail during the acceleration stage when eccentricity is zero. During the deceleration stage, the tails' high-regions will gradually transfer from the corners to the center. It should be noted that there are no distinct low-‍regions in the bodies of the robots during the deceleration stage. This phenomenon may be explained by the fact that the turbulence in the near-wall regions is significantly dissipated due to boundary layer effects. Meanwhile, the results from the cases with asymmetrical thrust force show that high-regions near the tail will gradually transfer to the side with the higher thrust force, while the significant dissipation by the head and the body will be weakened due to rotation. It is noteworthy that the asymmetrical thrust force may lead to a larger dissipation rate at the corner of the tail during the deceleration stage, implying that the robots' rotations result in a lower net production rate of turbulence around the separation point of the boundary layer.

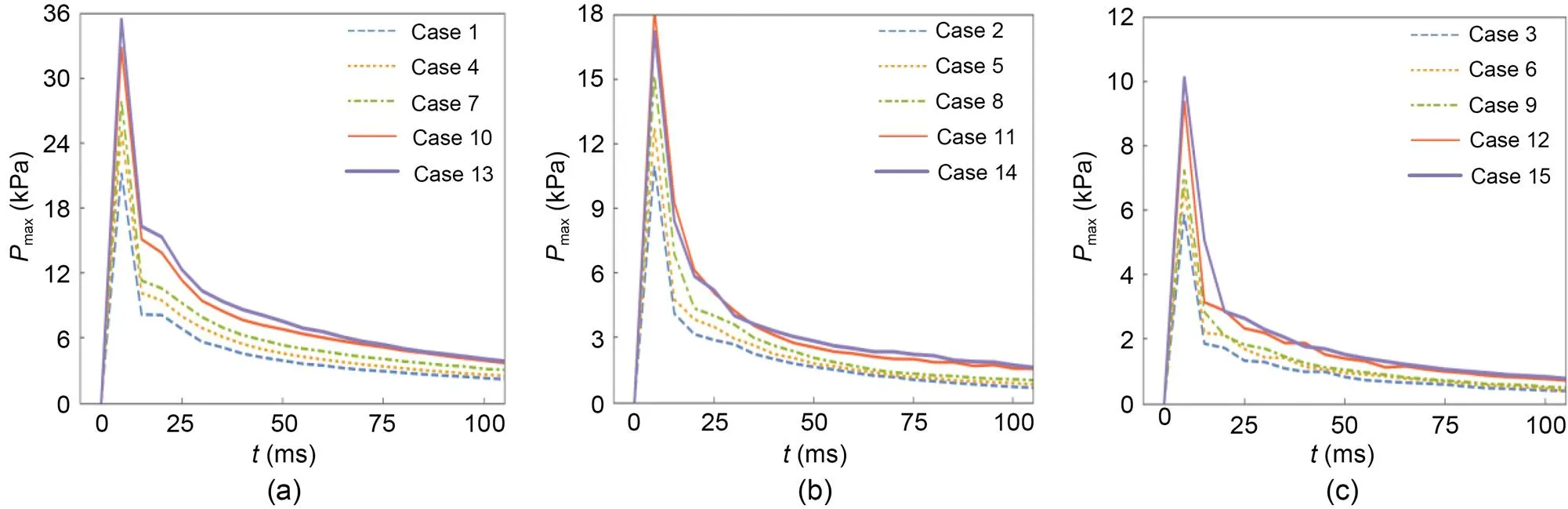
Fig. 7 Relationships between the maximum pressures Pmax and time: (a) e=e0; (b) e=e1; (c) e=e2

Fig. 8 Turbulence kinematic energy (k) distributions of cases 4–6 at t=0.01, 0.05, and 0.10 s

Fig. 9 Turbulence dissipation rate (ε) distributions of cases 4–6 at t=0.01, 0.05, and 0.10 s

4 Conclusions

The present study numerically investigated the hydrodynamics of robots driven by TDM. Focusing on the dependence of robot dynamics on thrust force and eccentricity, we obtained typical structures of turbulence fields around the robots to quantitatively analyze velocity distribution, vortex structures, pressure, and turbulence properties. The results demonstrate high-speed regions at both the heads and tails of robots due to sudden acceleration. They also uncover vortex systems at the corner on the side with higher thrust force, and indicate a negative relationship between the maximum fluid velocity and eccentricity. The maximum pressure on robot surfaces is shown to have a positive relationship with thrust force and a negative relationship with eccentricity. The model also provides the distribution of the turbulence kinetic energy and turbulence dissipation rate of the fluid field disturbed by robots, revealing the centripetal transference of the high-regions at the robots' tails and the existence of low-regions around their bodies due to boundary layer effects. Furthermore, the results concerning asymmetrical thrust force suggest that rotation of the robots, while it tends to increase turbulence, will decrease bothandat the head by moderating fluid compression.

We did not conduct experiments with multiple-actuation testing since the main objective was to develop a CFD model to investigate the fluid field when disturbed by high-speed motions of combustion-enabled soft robots. In future work, it will be necessary to investigate continuous fluid disturbances by multiple actuations. Due to tiny cavitation bubbles generated by the high-speed motions, the accuracy of the particle image velocimetry (PIV) validation is relatively coarse. Future studies can be carried out to investigate a high-accuracy PIV calibration algorithm that would effectively distinguish between the tiny bubbles and PIV particles. Another approach would be to improve the accuracy of the tiny-bubble-based PIV experimental method with creative statistical principles. Additionally, investigating the fluid field disturbances in terms of different robot geometries is a promising way to obtain an optimized robot design.

This study provides useful information for the study of robots' abilities during operating acceleration and steering tasks in the field of ocean engineering, and the findings are also applicable for the development of high-speed underwater vehicles.

This work is supported by the Key Research and Development Program of Zhejiang Province (No. 2021C03180), China, the Fundamental Research Funds for the Central Universities (No. 226-2022-00096), China, the Startup Fund of the Hundred Talent Program at Zhejiang University, China, the China Scholarship Council (No. 202006320349), and the Tezhi Program of Zhejiang Province (No. 2021R52049), China.

Zhiguo HE designed the research. Yang YANG processed the corresponding data. Yingzhong LOU and Guanzheng LIN wrote the first draft of the manuscript. Yang YANG helped to organize the manuscript. Pengcheng JIAO revised and edited the final version.

Yang YANG, Yingzhong LOU, Guanzheng LIN, Zhiguo HE, and Pengcheng JIAO declare that they have no conflict of interest.

Bai XJ, Shang JZ, Luo ZR, et al., 2022. Development of amphibious biomimetic robots., 23(3):‍157-187. https://doi.org/10.1631/jzus.A2100137

Bartlett NW, Tolley MT, Overvelde JTB, et al., 2015. A 3D-printed, functionally graded soft robot powered by combustion., 349(6244):161-165. https://doi.org/10.1126/science.aab0129

Calisti M, Picardi G, Laschi C, 2017. Fundamentals of soft robot locomotion., 14(130):20170101. https://doi.org/10.1098/rsif.2017.0101

Chen H, Zhu CA, Yin XZ, et al., 2007. Hydrodynamic analysis and simulation of a swimming bionic robot tuna., 19(4):412-420. https://doi.org/10.1016/S1001-6058(07)60134-6

Chu WS, Lee KT, Song SH, et al., 2012. Review of biomimetic underwater robots using smart actuators., 13(7):‍1281-1292. https://doi.org/10.1007/s12541-012-0171-7

Grissom MD, Chitrakaran V, Dienno D, et al, 2006. Design and experimental testing of the OctArm soft robot manipulator. Proceedings of SPIE 6230, Unmanned Systems Technology VIII, p.62301F. https://doi.org/10.1117/12.665321

Hamed AM, Vega J, Liu B, et al., 2017. Flow around a semicircular cylinder with passive flow control mechanisms., 58(3):22. https://doi.org/10.1007/s00348-017-2309-y

He ZG, Yang Y, Jiao PC, et al., 2022. Copebot: underwater soft robot with copepod-like locomotion., 0158:1-13. https://doi.org/10.1089/soro.2021.0158

Hu WQ, Lum GZ, Mastrangeli M, et al., 2018, Small-scale soft-bodied robot with multimodal locomotion., 554(7690):81-85. https://doi.org/10.1038/nature25443

Keithly D, Whitehead J, Voinea A, et al., 2018. A cephalopod-inspired combustion powered hydro-jet engine using soft actuators., 20:1-8. https://doi.org/10.1016/j.eml.2017.11.007

Launder BE, Spalding DB, 1974. The numerical computation of turbulent flows., 3(2):269-289. https://doi.org/10.1016/0045-7825(74)90029-2

Lee C, Kim M, Kim YJ, et al., 2017. Soft robot review., 15(1):3-15. https://doi.org/10.1007/s12555-016-0462-3

Li GR, Chen XP, Zhou FH, et al., 2021. Self-powered soft robot in the Mariana trench., 591(7848):66-71. https://doi.org/10.1038/s41586-020-03153-z

Li H, Go G, Ko SY, et al., 2016. Magnetic actuated pH-responsive hydrogel-based soft micro-robot for targeted drug delivery., 25(2):027001. https://doi.org/10.1088/0964-1726/25/2/027001

Li TF, Li GR, Liang YM, et al., 2016. Review of materials and structures in soft robotics., 48(4):‍756-766 (in Chinese). https://doi.org/10.6052/0459-1879-16-159

Lin GZ, Yang Y, He ZG, et al., 2022. Hydrodynamic optimization in high-acceleration underwater motions using added-mass coefficient., 263:112274. https://doi.org/10.1016/j.oceaneng.2022.112274

Loepfe M, Schumacher CM, Lustenberger UB, et al., 2015. An untethered, jumping roly-poly soft robot driven by combustion., 2(1):33-41. https://doi.org/10.1089/soro.2014.0021

Lou YZ, He ZG, Jiang HS, et al., 2019. Numerical simulation of two coalescing turbulent forced plumes in linearly stratified fluids., 31:037111. https://doi.org/10.1063/1.5087534

Majidi C, Shepherd RF, Kramer RK, et al., 2013. Influence of surface traction on soft robot undulation., 32(13):1577-1584. https://doi.org/10.1177/0278364913498432

Najem J, Sarles SA, Akle B, et al., 2012. Biomimetic jellyfish-inspired underwater vehicle actuated by ionic polymer metal composite actuators., 21(9):094026. https://doi.org/10.1088/0964-1726/21/9/094026

Renda F, Giorgio-Serchi F, Boyer F, et al., 2015. Locomotion and elastodynamics model of an underwater shell-like soft robot. Proceedings of the IEEE International Conference on Robotics and Automation, p.1158-1165. https://doi.org/10.1109/ICRA.2015.7139337

Rus D, Tolley MT, 2015. Design, fabrication and control of soft robots., 521(7553):467-475. https://doi.org/10.1038/nature14543

Shepherd RF, Stokes AA, Freake J, et al., 2013. Using explosions to power a soft robot., 52(10):2892-2896. https://doi.org/10.1002/anie.201209540

Soomro AM, Memon FH, Lee JW, et al., 2021. Fully 3D printed multi-material soft bio-inspired frog for underwater synchronous swimming., 210:106725. https://doi.org/10.1016/j.ijmecsci.2021.106725

Suzumori K, Endo S, Kanda T, et al., 2017. A bending pneumatic rubber actuator realizing soft-bodied manta swimming robot. Proceedings of IEEE International Conference on Robotics and Automation, p.4975-4980. https://doi.org/10.1109/ROBOT.2007.364246

Trivedi D, Rahn CD, Kier WM, 2008. Soft robotics: biological inspiration, state of the art, and future research., 5(3):99-117. https://doi.org/10.1080/11762320802557865

Umedachi T, Vikas V, Trimmer BA, 2013. Highly deformable 3-D printed soft robot generating inching and crawling locomotions with variable friction legs. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, p.4590-4595. https://doi.org/10.1109/IROS.2013.6697016

Villanueva A, Smith C, Priya S, 2011. A biomimetic robotic jellyfish (Robojelly) actuated by shape memory alloy composite actuators., 6(3):036004. https://doi.org/10.1088/1748-3182/6/3/036004

Wang G, Song YJ, Tang WS, et al., 2019. A numerical simulation analysis on bionic robot fish based on computational fluid dynamics (CFD) method., 14(3):400-407. https://doi.org/10.1166/jno.2019.2539

Wang HP, Yang Y, Lin GZ, et al., 2021. Untethered, high-speed soft jumpers enabled by combustion for motions through multiphase environments., 30(1):015035. https://doi.org/10.1088/1361-665X/abcaae

Wiguna T, Heo S, Park HC, et al., 2006. Mechanical design of biomimetic fish robot using LIPCA as artificial muscle., 326-328:1443-1446.

Yagmur S, Dogan S, Aksoy MH, et al., 2020. Turbulence modeling approaches on unsteady flow structures around a semi-circular cylinder., 200:107051. https://doi.org/10.1016/j.oceaneng.2020.107051

Yang Y, Hou BZ, Chen JY, et al., 2020. High-speed soft actuators based on combustion-enabled transient driving method (TDM)., 37:100731. https://doi.org/10.1016/j.eml.2020.100731

Sections S1–S5

Pengcheng JIAO, pjiao@zju.edu.cn

Pengcheng JIAO, https://orcid.org/0000-0002-9577-3828

June 26, 2022;

Revision accepted Aug. 11, 2022;

Crosschecked Sept. 2, 2022

© Zhejiang University Press 2022