Complex integrity constraint discovery:measuring trust in modern intelligent railroad systems

Wen-tao HU, Da-wei JIANG, Sai WU, Ke CHEN, Gang CHEN

Correspondence

Complex integrity constraint discovery:measuring trust in modern intelligent railroad systems

Wen-tao HU, Da-wei JIANG, Sai WU, Ke CHEN, Gang CHEN

Key Lab of Intelligent Computing Based Big Data of Zhejiang Province, Zhejiang University, Hangzhou 310027, China

1 Introduction

Data are at the heart of intelligent rail systems in the high-speed transportation sector (Zhou et al., 2020; Ho et al., 2021; Hu et al., 2021; Chen et al., 2022). The core of modern intelligent railroad systems typically includes rail transportation and equipment monitoring models learned from large datasets, which are often optimized for specific data and workloads (Zhu et al., 2019; Tan et al., 2020). While these intelligent railroad systems have been widely adopted and successful, their reliability and proper function will change as the data used changes. If the data used (on which the system operates) deviates from the fundamental constraints of the initial data (on which the system is trained) then, in that case, the system performance degrades, and the results inferred by the system model become unreliable, so the system model must be retrained and redeployed to re-store reliable inference results (Sharma and Chandel, 2013). The mechanism for assessing the trustworthiness of intelligent rail system inferences is of paramount importance, especially for rail systems performing safety-critical or high-impact operations.

Therefore, to measure the model's trustworthiness and achieve the safety and effectiveness of modern intelligent railroad systems, we need to address three challenges: (1) No labeled data. It is impractical to generate labeled data on train operations in real-time for operational traffic systems. (2) No access to the deployed model. For modern intelligent railroad systems, which require security and effectiveness, constant access to the deployed models not only creates security vulnerabilities but also affects the efficiency of model operations. (3) Real-time speculation on the trustworthiness of the inference results of the deployed model.

We argue that complex integrity constraints provide an efficient and robust mechanism to quantify the confidence of models deployed by intelligent railway systems in inferences about service data (Hu et al., 2020). The reasons for this are: (1) Complex integrity constraints are constructed without expert experience and are generated spontaneously from the distribution characteristics of the dataset itself; (2) Complex integrity constraints analyze the consistency of data rather than reading the entire model; (3) Complex integrity constraints determine whether data are consistently based on tuples rather than tuple pairs, which ensures that the consistency of data can be verified without scanning historical data. By measuring the proportion of data that violates the constraints, complex integrity constraints provide a more efficient and robust mechanism for verifying the trustworthiness of the application's data (Bai et al., 2022).

Complex integrity constraints belong to the category of data parsing, which refers to extracting specific metadata from the dataset. Functional dependencies (FDs) (Huhtala et al., 1999; Fan et al., 2020; Livshits et al., 2020; Wu et al., 2020; Kossmann et al., 2022) and their variants obtain the existence of a relationship between two sets of attributes without providing an expression in the form of parameters (Fan et al., 2011; Caruccio et al., 2016; Kruse and Naumann, 2018). Another more complex technique, the denial constraint (DC), can contain many different constraints, such as FD and its variants (Bleifuß et al., 2017; Berti-Équille et al., 2018; Pena et al., 2021). However, this can make the constraints highly complex and large, and it would be challenging to sift through them to find potentially useful information. Pattern functional dependency (PFD) aims to address the deficiencies in DC, but it targets attributes whose values are text. This is not applicable for intelligent rail systems where most attributes are numeric. By using regular expressions and coding numbers as characters, constraints with different semantics are quickly detected (Pena et al., 2019; Qahtan et al., 2020).

In this paper, we use a novel approach to data analysis where complex integrity constraints are used to describe the data. If the data violate a complex integrity constraint, it indicates that the model deployed by the intelligent railroad system is likely to be unreliable. Complex integrity constraints specify constraints on the algebraic relationships of multiple numerical attributes involved in the data. We believe that data that conform to the complex integrity constraint allow the model to infer results more accurately than if it conforms to the distributional properties. Any data that violate the complex integrity constraint may cause the failure of a model built to conform to complex integrity. We can therefore use the violation of complex integrity constraints by data to represent the trust of a model deployed in an intelligent railroad system using that data.

An example of trustworthy modern intelligent transportation systems and complex integrity constraints is provided in Data S1 in the electronic supplementary materials (ESM), including technical details of data indexing, theorems for constrained inference systems, and the definition of plausible machine learning. The definition of complex integrity constraints and the discovery algorithm are shown in Section 2. Section 3 presents experiments on trusted machine learning and complex integrity constraints to analyze the algorithm's performance. The complete experimental setup is shown in Data S1.

2 Object and methods

2.1 Complex integrity constraint

1. Basic notations

2. Complex integrity constraint

3. Semantics

The semantics of complex integrity constraints consists of the following forms:

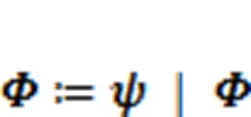
4. Violations

2.2 Complex integrity constraint system

The complex integrity constraint attempts to solve the model trustworthiness problem of intelligent railroad system deployment by inputting the train operation data collected by the intelligent railroad system, such as operation mileage, energy loss, average speed, and carload. Fig. 1 shows the overall framework of the system operation. The system constructs an index and uses constraint inference and search space pruning techniques to achieve the fast discovery of constraints. After that, the system uses the discovered constraints to analyze the credibility of the deployed models, thus ensuring that the intelligent railroad system can reliably apply the models for train operation control, condition monitoring, and fault warning.

Fig. 1 Structure of a complex integrity constraint system

1. BitVectors

Fig. 2 shows the two categorical attribute vectors corresponding to seven tuples.

Fig. 2 Internals of BitVector

2. Support pruning

Support pruning is adopted from frequent itemset mining which finds sets of items whose frequency exceeds a given threshold. In our application, the concept of support is measured by the frequency of attribute combinations:

3. Efficient discovery constraint algorithm

Given one table and one parameter, the algorithm outputs the set of complex integrity constraints. The algorithm first vectorizes all tuples and obtains the categorical and numerical attributes. Then an index is constructed based on the vectors, which is used to perform queries and computations quickly afterward. Since all the tuples in the table have been vectorized, we can directly calculate the number of different values of each attribute and classify those as categorical attributes, and then traverse the categorical attributes to find all the attribute values with support more significant than a threshold. After that, the algorithm starts to find all the derived attributes. First, all numerical attributes are traversed and paired with other attributes, and the correlation coefficient of the attribute pair is computed. If it is not equal to 0, the correlation is considered. Then, algebraic operations are performed on the correlated attribute pairs to generate the corresponding derived attributes. Finally, after obtaining the candidate sets of categorical attribute values and derived attributes, we iterate through each set of categorical attribute values and calculate the mean and variance of the tuple on the derived attributes. The result is returned after traversal.

3 Results and discussion

3.1 Applicability

We now show the applicability of complex integrity constraints to trusted machine learning problems (Ak et al., 2016). We show that tuples that violate complex integrity constraints on training data are unsafe. Thus, a machine learning model deployed in an intelligent transportation system is more likely to perform poorly on these tuples.

We designed a regression task to predict train velocity and trained a linear regression model for this task. Our goal is to observe whether the mean absolute error (MAE) of the prediction is related to the constraints violated by the data. Our experiment consists of the following steps: (1) AUDITOR performs a complex integrity constraint search on the dataset while ignoring the target attributes. (2) We calculate the average violation ratio in the Xiamen subway operation dataset. (3) We train a linear regression model in the dataset to predict the train operation speed. (4) We calculate the MAE (Ranjan et al., 2021) of the model prediction accuracy in the dataset. As shown in Fig. 3, we divide the Xiamen subway dataset into three parts based on time: morning, afternoon, and evening. The solid blue line is the actual data of the train operation, and the solid green line is the data inferred from the linear regression model. The results of model inference from 12‍–‍18 h are closer to the actual data (minimum MAE) compared to other periods, and the average percentage of violation data in this period is also the smallest. We find that the violation of constraints is an excellent feature of the prediction errors because they are correlated in the way they vary in the dataset. The model implicitly assumes that the constraints derived by AUDITOR will always hold, and thus the situation deteriorates when that assumption does not hold.

Table 1 Average constraint violation and MAE (for liner regression) of four data splits on the Xiamen subway dataset. The constraints were learned on a train, excluding the target attribute

3.2 Comparison with the state-of-the-art

In this set of experiments, we compare AUDITOR against state-of-the-art unsupervised anomalous detection approaches, the K-nearest neighbors (KNN) (Malini and Pushpa, 2017), and the Cluster method (Azzedine et al., 2021) by measuring the precision recall arear under curve (PR-AUC) (Fig. 4) (Kieu et al., 2019).

Fig. 3 Comparison of actual and model-inferred speeds of trains at different periods. Speeds below 0 indicate the opposite direction of travel. References to color refer to the online version of this figure

Fig. 4 Evaluation of state-of-the-art works: PR-AUC

For the PR-AUC of the night dataset, as shown in Fig. 4, KNN achieves the lowest PR-AUC. For example, KNN has a PR-AUC of 51%, while the PR-AUC of Cluster method is 55%.

However, all these methods are far worse than the proposed method AUDITOR-KDE. For example, in the train dataset, AUDITOR-Base and AUDITOR-KDE (kernel density estimation) have PR-AUC of 58% and 68%, respectively, which are more than 15% higher than Cluster (53%) and KNN (50%). AUDITOR leverages implicit relationships between categorical and numerical attributes, while these inliers are misclassified as anomalous by the unsupervised algorithms.

For the afternoon dataset in Fig. 4, AUDITOR outperforms these unsupervised algorithms. For example, AUDITOR-KDE has a high PR-AUC of 66%, while the PR-AUC values of the other methods are 56% (Cluster) and 54% (KNN), respectively.

For the morning dataset, AUDITOR-KDE has a PR-AUC of 70%, while the PR-AUC values of the other methods are 59% (Cluster) and 56% (KNN), as shown in Fig. 4. For the response time of the train dataset, as shown in Fig. 5, AUDITOR-Base performs better than the other approaches. For example, in the train dataset, AUDITOR-Base has a response time of 55 s, which is lower than that of KNN (143 s), Cluster (168 s), and AUDITOR-KDE (437 s). The AUDITOR-Base method obtains an efficient index rather than any single method. Our AUDITOR still performs the best among all approaches. For instance, in the night dataset, AUDITOR-Base has a response time of 12 s, while the response times of the other methods are 76 s (Cluster), 88 s (KNN), and 125 s (AUDITOR-KDE), respectively. AUDITOR-Base leverages vector computation of low consumption. Similarly, for the morning and afternoon datasets, AUDITOR-Base outperforms the others, as shown in Fig. 5.

Fig. 5 Evaluation of state-of-the-art works: response time

4 Conclusions

In this paper, we present a system for automatically discovering complex integrity constraints and the concept of unsafe tuples for trusted machine learning. The system uses algebraic operations to discover hidden relationships between categorical and numerical attributes in a dataset. The system uses the BitVector index structure to speed up the computation of sums, means, and variances as a matrix framework to construct vector to represent graph element features. This effectively reduces the bounds of the normal range. Experiments validate our theory that complex integrity bounds provide an efficient and robust mechanism to quantify the trust of inferences from models deployed by intelligent railroad systems on data.

This work is supported by the Key Research and Development Program of Zhejiang Province of China (No. 2021C01009) and the Fundamental Research Funds for the Central Universities, China.

Wen-tao HU, Da-wei JIANG, Sai WU, Ke CHEN, and Gang CHEN designed the research. Wen-tao HU wrote the first draft of the manuscript. Da-wei JIANG and Sai WU participated in the theoretical model design. Ke CHEN processed the corresponding data. Gang CHEN helped to make the experiment and organize the manuscript. Wen-tao HU and Gang CHEN revised and edited the final version.

Wen-tao HU, Da-wei JIANG, Sai WU, Ke CHEN, and Gang CHEN declare that they have no conflict of interest.

Ak R, Fink O, Zio E, 2016. Two machine learning approaches for short-term wind speed time-series prediction., 27(8):1734-1747. https://doi.org/10.1109/TNNLS.2015.2418739

Azzedine B, Zheng LN, Alfandi O, 2021. Outlier detection: methods, models, and classification., 53(3):1-37. https://doi.org/10.1145/3381028

Bai QB, Bedi AS, Agarwal M, et al., 2022. Achieving zero constraint violation for constrained reinforcement learning via primal-dual approach. Proceedings of the 36th AAAI Conference on Artificial Intelligence, p.3682-3689.

Berti-Équille L, Harmouch H, Naumann F, et al., 2018. Discovery of genuine functional dependencies from relational data with missing values., 11(8):880-892. https://doi.org/10.14778/3204028.3204032

Bleifuß T, Kruse S, Naumann F, 2017. Efficient denial constraint discovery with hydra., 11(3):311-323. https://doi.org/10.14778/3157794.3157800

Caruccio L, Deufemia V, Polese G, 2016. Relaxed functional dependencies—a survey of approaches., 28(1):147-165. https://doi.org/10.1109/TKDE.2015.2472010

Chen HT, Jiang B, Ding SX, et al., 2022. Data-driven fault diagnosis for traction systems in high-speed trains: a survey, challenges, and perspectives., 23(3):‍‍1700-1716. https://doi.org/10.1109/TITS.2020.3029946

Fan WF, Geerts F, Li JZ, et al., 2011. Discovering conditional functional dependencies., 23(5):683-698. https://doi.org/10.1109/TKDE.2010.154

Fan WF, Hu CM, Liu XL, et al., 2020. Discovering graph functional dependencies., 45(3):15. https://doi.org/10.1145/3397198

Ho LV, Nguyen HD, de Roeck G, et al., 2021. Damage detection in steel plates using feed-forward neural network coupled with hybrid particle swarm optimization and gravitational search algorithm., 22(6):467-480. https://doi.org/10.1631/jzus.A2000316

Hu QX, Long JS, Wang SK, et al., 2021. A novel time-span input neural network for accurate municipal solid waste incineration boiler steam temperature prediction., 22(10):777-791. https://doi.org/10.1631/jzus.A2000529

Hu WT, Zhang DX, Jiang DW, et al., 2020. AUDITOR: a system designed for automatic discovery of complex integrity constraints in relational databases. Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, p.2697-2700. https://doi.org/10.1145/3318464.3384683

Huhtala Y, Kärkkäinen J, Porkka P, et al., 1999. Tane: an efficient algorithm for discovering functional and approximate dependencies., 42(2):‍100-111. https://doi.org/10.1093/comjnl/42.2.100

Kieu T, Yang B, Guo CJ, et al., 2019. Outlier detection for time series with recurrent autoencoder ensembles. Proceedings of the 28th International Joint Conference on Artificial Intelligence, p.2725-2732. https://doi.org/10.24963/ijcai.2019/378

Kossmann J, Papenbrock T, Naumann F, 2022. Data dependencies for query optimization: a survey., 31(1):‍1-22. https://doi.org/10.1007/s00778-021-00676-3

Kruse S, Naumann F, 2018. Efficient discovery of approximate dependencies., 11(7):759-772. https://doi.org/10.14778/3192965.3192968

Livshits E, Kimelfeld B, Roy S, 2020. Computing optimal repairs for functional dependencies., 45(1):4. https://doi.org/10.1145/3360904

Malini N, Pushpa M, 2017. Analysis on credit card fraud identification techniques based on KNN and outlier detection. Proceedings of the 3rd International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics, p.255-258. https://doi.org/10.1109/AEEICB.2017.7972424

Pena EHM, de Almeida EC, Naumann F, 2019. Discovery of approximate (and exact) denial constraints., 13(3):266-278. https://doi.org/10.14778/3368289.3368293

Pena EHM, de Almeida EC, Naumann F, 2021. Fast detection of denial constraint violations., 15(4):859-871. https://doi.org/10.14778/3503585.3503595

Qahtan A, Tang N, Ouzzani M, et al., 2020. Pattern functional dependencies for data cleaning., 13(5):684-697. https://doi.org/10.14778/3377369.3377377

Ranjan KG, Tripathy DS, Prusty BR, et al., 2021. An improved sliding window prediction-based outlier detection and correction for volatile time-series., 34(1):e2816. https://doi.org/10.1002/jnm.2816

Sharma V, Chandel SS, 2013. Performance and degradation analysis for long term reliability of solar photovoltaic systems: a review., 27:753-767. https://doi.org/10.1016/j.rser.2013.07.046

Tan P, Li XF, Xu JM, et al., 2020. Catenary insulator defect detection based on contour features and gray similarity matching., 21(1):64-73. https://doi.org/10.1631/jzus.A1900341

Wu PZ, Yang W, Wang HC, et al., 2020. GDS: general distributed strategy for functional dependency discovery algorithms. Proceedings of the 25th International Conference on Database Systems for Advanced Applications, p.270-278. https://doi.org/10.1007/978-3-030-59410-7_17

Zhou P, Li T, Zhao CF, et al., 2020. Numerical study on the flow field characteristics of the new high-speed maglev train in open air., 21(5):366-381. https://doi.org/10.1631/jzus.A1900412

Zhu L, Yu FR, Wang YG, et al., 2019. Big data analytics in intelligent transportation systems: a survey., 20(1):‍383-398. https://doi.org/10.1109/TITS.2018.2815678

Data S1

Da-wei JIANG, https://orcid.org/0000-0002-1890-4046

Sai WU, https://orcid.org/0000-0002-7903-1496

Gang CHEN, https://orcid.org/0000-0002-7483-0045

Mar. 23, 2022;

Revision accepted Aug. 18, 2022;

Crosschecked Sept. 15, 2022

© Zhejiang University Press 2022