基于贝叶斯网络的尾矿库溃坝风险动态评价*

崔旭阳，叶义成,2，胡南燕，周 栋 ，谭文侃 ，黄兆云

(1.武汉科技大学 资源与环境工程学院,湖北 武汉 430081；2.湖北省工业安全工程技术研究中心,湖北 武汉 430081；3.湖北景深安全技术有限公司,湖北 宜昌 443000)

0 引言

尾矿库是金属、非金属矿山等排出的在当前技术条件下不具有工业利用价值的矿物以及化工厂排出的工业废渣堆存的场所，是维持矿山和化工厂正常生产不可缺少的设施。堆存的尾矿具有潜在的经济价值，同时也存在尾矿坝溃坝风险，一旦发生溃坝，将会给下游居民和环境造成严重危害[1]。随着经济的快速发展，我国矿业开发规模越来越大，尾矿量不断增加，我国是目前尾矿排放量最多的国家之一，尾矿库数量居于世界前列。由于历史原因，大多数尾矿坝呈现中小型坝占比大、安全等级偏低、上游法筑坝比例高的特点；尾矿库周边环境复杂，尾矿坝的稳定性极易受到自然和人为因素的影响。科学合理的尾矿库溃坝风险评价是遏制尾矿库溃坝灾害发生的重要途径之一。

尾矿库安全评价方法主要有层次分析法、有限元理论、模糊综合评价、事故树法、统计分析法等。柯丽华等[2-3]应用集对可拓耦合算法和EAHP模糊综合评价模型对尾矿库溃坝风险进行了分析，结果表明，该模型降低了评价过程中的主观性。LI 等[4]根据固有风险和频率风险建立了评价指标体系，采用动态灰色关联分析法对尾矿坝的破坏预警等级进行了评价，避免了繁琐的测试和静态预警状态的风险。陈虎等[5]基于ISM模型建立了表征因素关联关系的尾矿库溃坝风险分级方法，避免了因素关联模式对尾矿库溃坝分级的干扰，同时克服了权重确定的主观性过高的缺点。梁玉霞等[6]基于边界条件和计算公式构建了尾矿库溃坝风险量化分析模型，分析了地震烈度对尾矿库溃坝风险的影响。董译萱等[7]应用博弈论-有限元模型对尾矿库溃坝风险进行了评价，完善了风险等级间的模糊性问题。现有尾矿库溃坝风险评价研究主要侧重于尾矿库运行阶段的坝体静态风险评估，针对动态风险评估的研究相对较少，缺乏尾矿库风险动态演化研究，未考虑风险因素的连续性和发展性。赵怡晴等[8]提出了一种面向尾矿库生命周期的隐患及事故主要影响因素的识别方法，表征了事故影响因素的相互作用关系以及溃坝事故风险的演化规律；覃璇等[9]构建了演化复杂网络对尾矿库生命周期阶段的隐患进行了辨识，发现时间变化可引发尾矿库系统灾变。

贝叶斯网络已广泛应用于智能推理、病害检测、可靠性分析等领域[10-11]。尾矿库溃坝致灾因素复杂，溃坝事故的发生不是由单个因素引起的，而是由多个因素在时间推移下互相传递、相互影响并在一定的环境条件、现实条件等综合作用下持续演化而发生的。动态评价刻画了尾矿库溃坝风险状态的实时变化趋势，有效避免了评估结果不全面的问题，更加贴近尾矿库系统的真实状况，评价结果更加真实可靠。本文通过有效识别尾矿库的溃坝风险因素，基于改进的动态加权贝叶斯网络模型对尾矿库系统中的溃坝风险因素进行了定量分析，以期科学识别和评估尾矿库溃坝风险和演化规律。

1 尾矿库溃坝风险评价指标体系

影响尾矿库溃坝的风险因素众多，某些风险因素会随着时间的推移影响其他风险因素的发生程度和概率。因此，尾矿库安全风险评估的关键是对尾矿库进行风险辨识。基于人员、环境、管理和尾矿库自身等4个方面系统地对尾矿库溃坝事故进行致因要素分析，有效识别风险因素。尾矿库的溃坝机理主要为坝体失稳、洪水漫顶、渗透破坏和管理风险。建立包含坝体水平位移、干滩长度、安全超高、日降雨量、浸润线埋深、坝体渗流量6个动态指标以及排洪能力系数、安全管理系数等11个静态指标的尾矿库溃坝风险指标体系(见图1)，以此为依据进行风险识别与评估。动态指标是尾矿库系统实时更新的监测数据，具有时序性，是尾矿库溃坝风险评价的重要组成部分。

图1 尾矿库溃坝风险评价指标体系

2 基于Kendall相关系数的组合权重和时间权重确定

2.1 基于Kendall相关系数的指标重要度排序

应用Kandall和谐系数[12]解决不同专家对评价指标重要程度意见不一致的情况，对评价指标排序信息进行筛选，淘汰严重不一致的专家排序，最终确定指标的理想排序，以此降低专家评价差异较大对评价结果的不利影响。Kendall和谐系数的计算式为

(1)

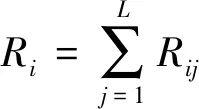
2.2 最优组合权重确定

应用DEA数据包络法和熵值法两种赋权方法[13]对尾矿库溃坝风险评价指标体系中的17个评价指标进行赋权，权重系数μ能够使指标评价值尽可能地分散，不同权重系数体现被评价指标间的差异。基于最小方差原理构建最优化模型[见式(2)]并计算权重系数,通过式(3)得到μ1,μ2,…,μm的值，最后计算出各评价指标的最优组合权重。

(2)

(3)

式中，μt为权重系数，w0为集成权重，wk为已知权重。

2.3 时间权重

动态评价问题是由时间、被评价对象和指标构成的三维综合评价问题，m个指标x1,x2,…,xm按照时间顺序t1,t2,…,tn建立在不同时间段的时序数据表，考虑了尾矿坝在运行期间随着坝体堆积高度和库容的不断增加，潜在的溃坝风险也随着时间的推移逐渐增大。时间权重表示在动态评价中对不同时间段信息的重视程度。对于某一时刻的评价结果而言，之前不同时间数据信息对其的重要性往往不同，有效确定时间权重是求得合理评价结果的关键，采用改进“厚今薄古”思想[14]的连续函数时间权重计算方法求取各个时刻的时间权重，可以提高监测数据在不同时间间隔下确定权重的准确性。时间权重和时间折现系数的计算式分别为

(4)

(5)

式中，τt为第t个时刻的时间权重，λt为时间折现系数。

共识问题，首先在数学界受到关注。早在1959年，EISENBERG E和GALE D研究了特定条件下如何在一组个体中形成共识概率分布问题。随后共识问题受到了不同学界的广泛关注。

3 动态加权贝叶斯网络模型

贝叶斯网络被描述为有向无环图(DAG)，是一种将概率论知识作为理论基础并与图论相结合作为表达手段的因果网络[15]。贝叶斯网络的优势在于能将各种不确定性信息进行整体处理并推理运算，在解决不确定性问题上具有成熟的应用基础。尾矿库溃坝风险因素较多，同结构层次间风险指标关联耦合。传统的贝叶斯网络中各节点相互独立，因此需对贝叶斯网络中的不同节点变量分配不同的权重以增强节点之间的关联性。对贝叶斯网络中的不同节点变量赋予时间权重以体现尾矿库溃坝风险的实时动态变化，改进的后验概率推理公式为

(6)

式中，νni和Anj分别为第n个时间段中第i个父节点和第j个子节点的取值状态，P(νni)为父节点的先验概率分布，wi为各个节点的权重值，P(Anm|νni)wi为各个节点加权后的概率。

3.1 网络结构确定

贝叶斯网络结构学习用于确定模型中各变量之间的关系。选择合适的节点变量是构建科学可信的贝叶斯网络的基础。以尾矿库溃坝风险评价指标体系各指标作为贝叶斯网络的节点变量，以有向线段表达不同节点变量之间的关系，根据变量间的关联关系绘制节点间的有向边，最后根据专家经验及知识优化模型结构构建出贝叶斯网络拓扑结构(见图2)。

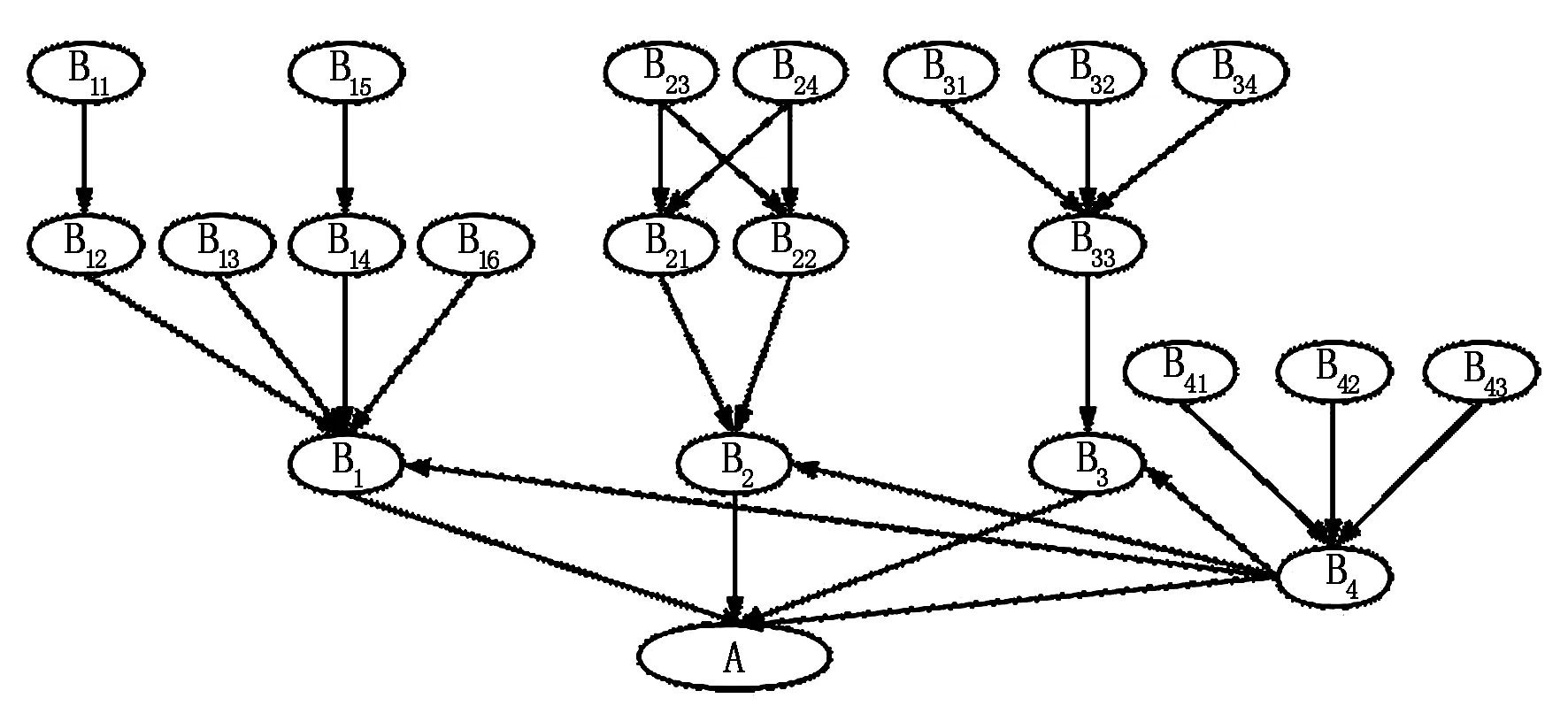
图2 尾矿库溃坝风险贝叶斯网络结构

由图2可知，尾矿库溃坝风险贝叶斯网络共包含22个风险隐患节点，系统地表征了影响尾矿库溃坝的各风险节点间的关联关系。节点变量的集合为{A, B1, B2, B3, B4, B11, B12, …}，其中包括1个尾矿库溃坝子节点，12个父节点和9个中间节点，子节点代表尾矿库发生溃坝的风险概率，父节点对应的概率为先验概率，父节点与中间节点之间的关联程度为条件概率。

3.2 参数学习

根据调研事故统计数据及专家经验确定父节点的先验概率，由不同风险因素之间的相互关系确定条件概率表(CPT)。在构造贝叶斯网络结构的基础上，借助条件概率赋予贝叶斯网络数学意义，从而使贝叶斯网络模型可以定性和定量地解决实际问题。尾矿库溃坝事故是一类高危低频事故，样本数据不完整。依据网络结构关系，利用样本数据通过区间数排序[16]改进传统条件概率的推理计算，避免了仅凭历史数据和专家经验确定参数条件概率分布的主观性。定性指标与定量指标规范化的计算式分别为

(7)

(8)

(9)

式中，rij=[rijL,rijU]，aij为第i个风险等级下第j个指标的取值，z为综合评价指标。

4 动态加权贝叶斯网络尾矿库溃坝风险评价模型

尾矿库系统是由相互关联的人员、环境、管理及尾矿库自身四个层面组成的，层面间及层面内各指标相互影响，单个风险因素可能会影响同一层、不同层甚至整个系统中的其他指标[17]，考虑风险指标间的相互作用，构建尾矿库溃坝风险动态加权贝叶斯网络模型。

首先，选取6位专家对一级评价指标和二级评价指标重要度排序的意见，通过式(1)算得Kendall和谐系数W=0.829。采用一致性检验对信息进行筛选，依据指标理想排序(见表1)确定判断矩阵，最后计算出指标的权重(见表2)。

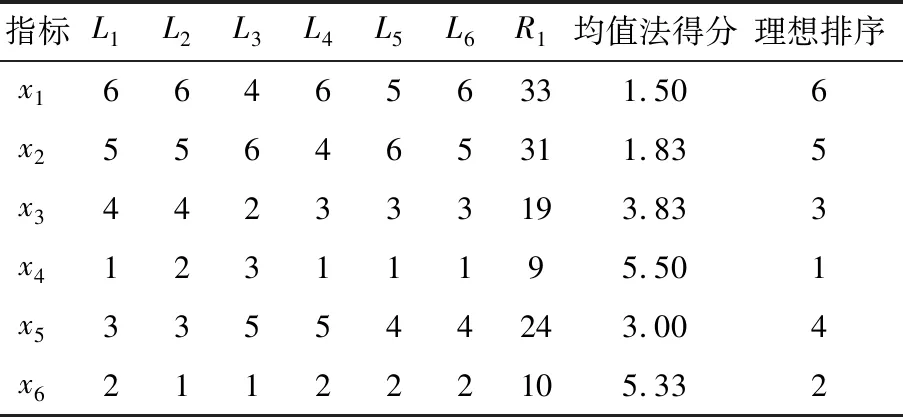
表1 指标的专家排序和理想排序

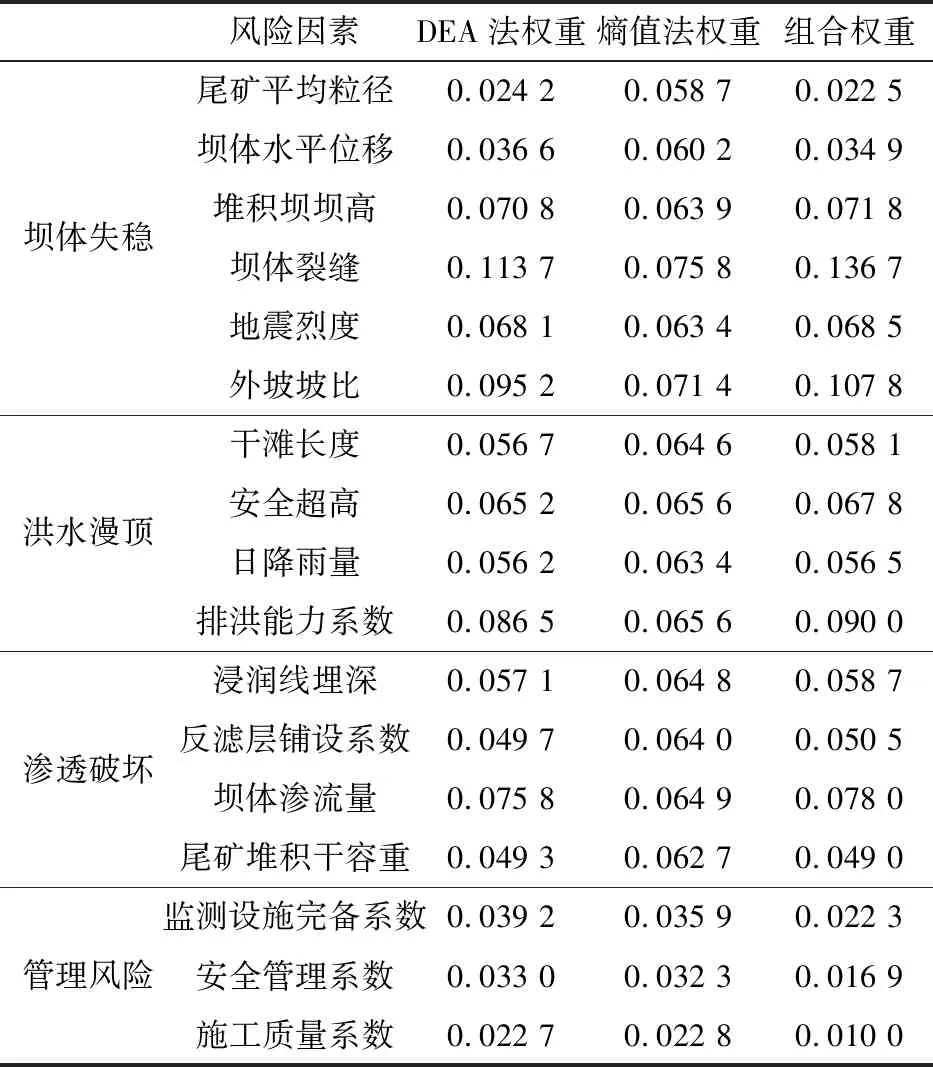
表2 评价指标权重

贝叶斯网络通过有向边捕获父节点和子节点间的条件概率，通过建立每个子节点的条件概率表(CPT)显示子节点状态与父节点之间的依存关系。由于尾矿库溃坝事故发生概率小，有些节点会由于缺少历史数据而无法正确填充其CPT，故不能确定相应的概率分布函数或其参数，一般由领域专家判断得出的主观条件概率填补。为避免主观片面性，利用模糊区间对在不同等级的风险指标作用下的区间数结合指标区间权重进行区间数排序，根据最终排序设定条件概率。

以DB13/T 2260-2015《尾矿库重大危险源辨识与分级》、AQ 2030-2010《尾矿库安全监测技术规范》、《尾矿坝设计手册》等的相关规定和已有的尾矿库溃坝风险分级研究成果为依据，建立尾矿库溃坝风险指标分级标准(见表3)。

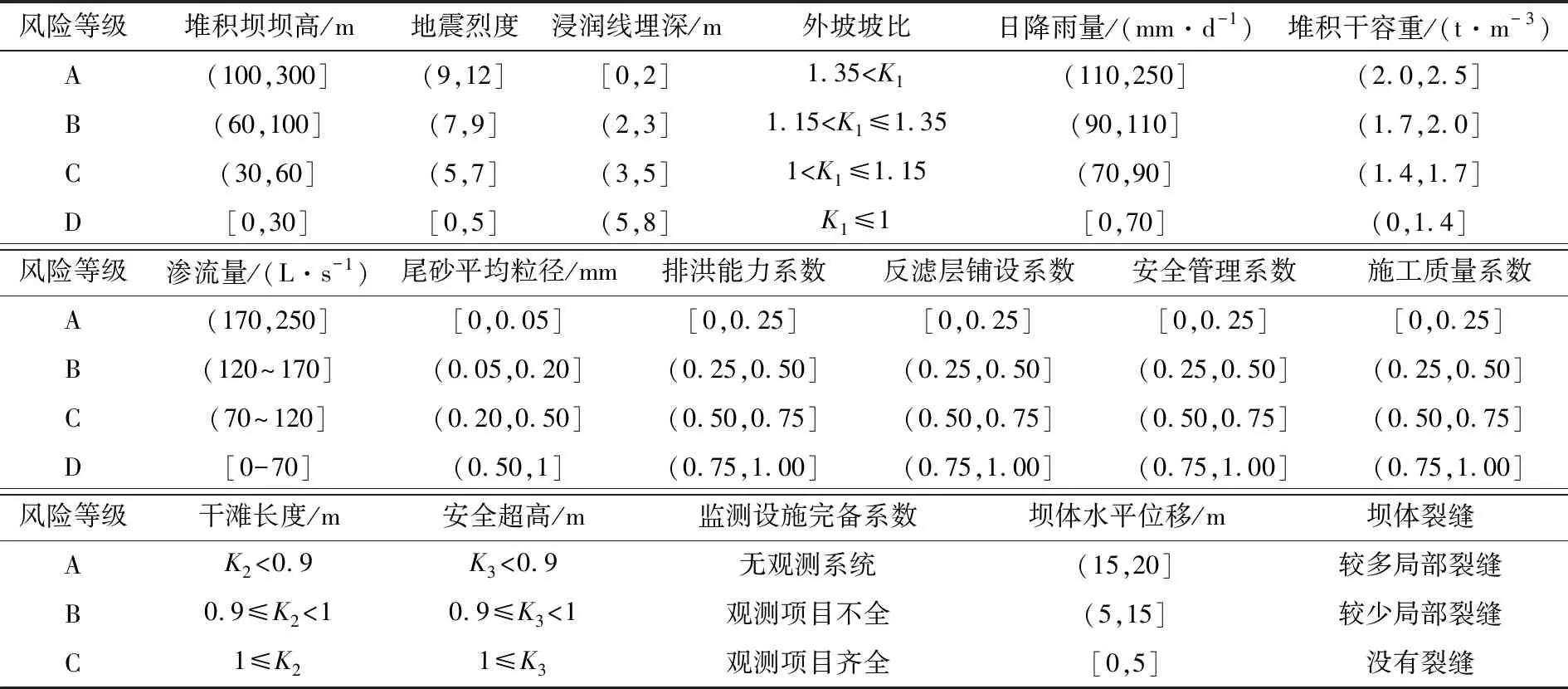
表3 尾矿库二级风险指标分级

以日降雨量和排洪能力两个父节点为例，通过式(7)和式(8)计算得到规范化后的评价指标区间数值，通过式(9)计算得到不同日降雨量与排洪能力系数的综合评价指标区间数值(见表4)。

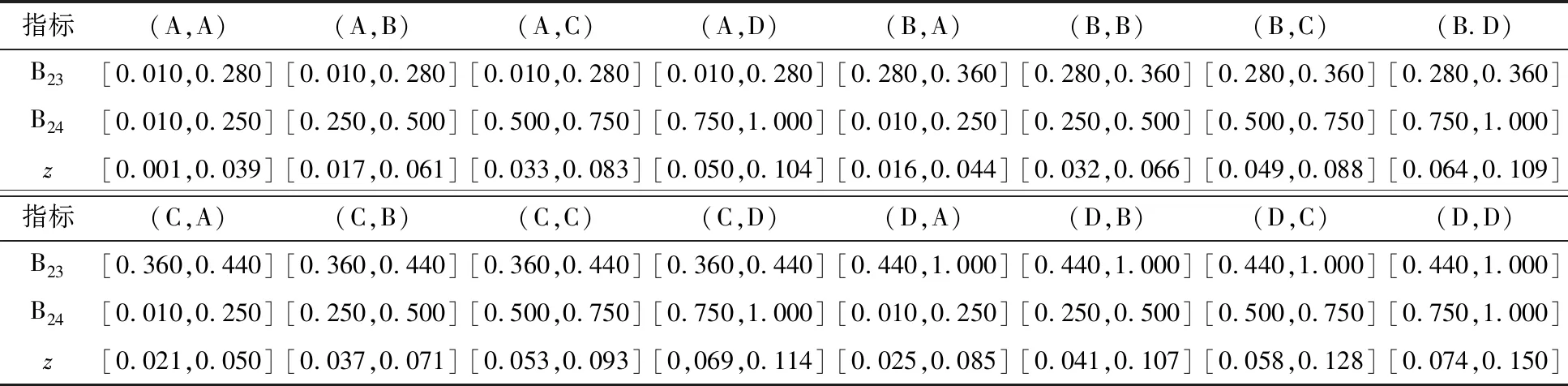
表4 规范化后的不同日降雨量与排洪能力系数的综合评价指标区间数值

考虑这些风险因素的相互作用，嵌入指标权重以增强节点之间的关联性，为了对整个尾矿库系统的风险进行建模并获取随时间推移的系统动态性，在传统贝叶斯网络模型的基础上引入时间概念，将静态综合评价转换为动态综合评价，计算出加权条件概率。最后，基于二维信息的区间数排序法进行排序，确定各指标在不同风险等级下对其子节点诱发风险的概率排序，补足条件概率表中的全部数据，构建完整的评价模型。

将各节点的先验概率及加权条件概率输入Netica软件建立尾矿库溃坝风险贝叶斯网络模型(见图3)。图3中父节点B11-B43表示风险指标，中间节点A1-A4表示溃坝事故发生的风险类别，目标节点P表示溃坝风险，A、B、C、D表示各节点的风险等级。以某二等尾矿库为例，其排洪设施完整，尾矿库日常管理完善，监测系统完备，根据尾矿库60 d内的指标监测值(见图4)。利用动态加权贝叶斯网络模型进行尾矿库溃坝事故风险的后验概率推理。分别计算原始贝叶斯网络模型和改进动态加权贝叶斯网络模型的评价结果，得到的对比曲线如图5所示。由图5可知：该尾矿库总体处于低风险状态，与实际情况相符；第32 d-第36 d、第48 d-第52 d和第58-第60 d因遇强降雨，该尾矿库溃坝风险等级升高。引入指标权重和时间权重的改进模型降低了因指标监测数据波动产生的影响，评价结果更为合理。

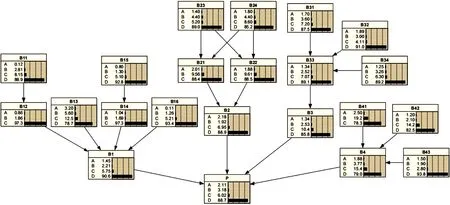
图3 尾矿库溃坝贝叶斯网络模型

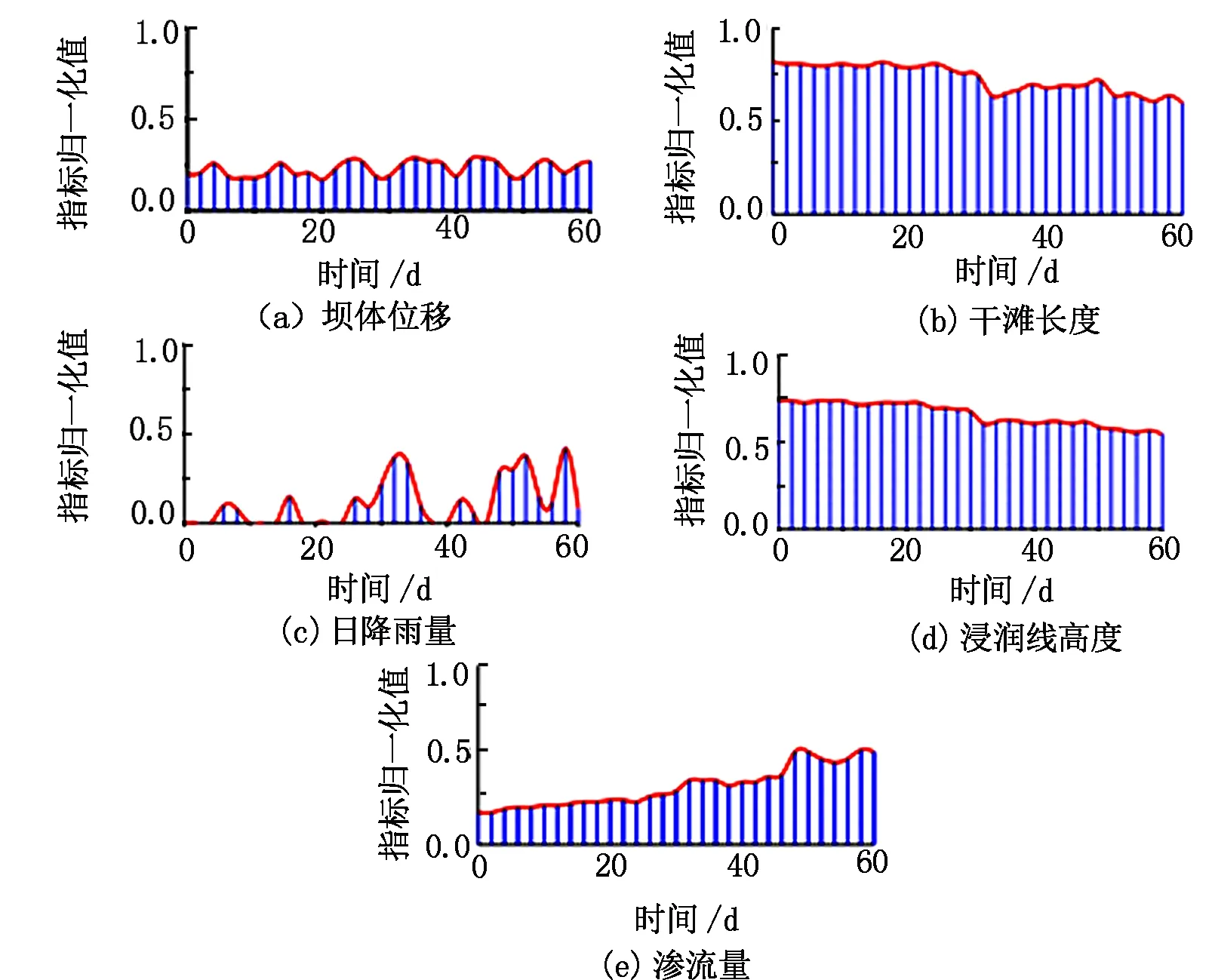
图4 指标监测值

图5 尾矿库溃坝风险等级评价结果

5 结论

a.建立了嵌入时间权重和指标权重的动态加权贝叶斯网络模型，引入指标权重增强了节点之间的相关性，引入时间权重体现了评价过程中对不同时刻的重视程度，增强了动态综合评价结果的客观性。

b.构建包含动态指标和静态指标的尾矿库溃坝风险评价指标体系，使用基于Kendall相关系数的DEA数据包络法和熵值法组合赋权确定评价指标权重系数，解决了专家在指标重要程度排序中意见不一致而导致评价结果可信度降低的问题，有效降低了单一赋权法的随意性和模糊性。

c.采用区间数排序法在贝叶斯网络模型条件概率学习参数不足的情况下进行推理，得到基于历史数据和专家经验的加权条件概率表，改进了数据不全时仅凭专家经验确定条件概率的主观随意性。

d.应用改进的动态加权贝叶斯网络评估模型对某尾矿库60 d的监测数据进行分析，发现评价结果与实际相符，验证了模型的有效性和实用性。