设计：让数学教学实现增值性发展——以“小数的意义建构”为例

王岚

从知识传授到素养培育，从单一维度到立体视角，从关注当下到指向未来，课堂需要变革，教学需要增值。教师可以以设计为载体，以素养为核心，基于学科超越学科，基于儿童为了儿童，实现教学的增值性发展。下面，笔者以“小数的意义建构”为例，谈谈如何通过设计让数学教学增值。

一、夯实增值的根基：理解教材的编排特点

小学数学课程的内容结构包括显性的知识结构和隐性的思想方法结构。数学教材中既有数学知识的逻辑结构，又有数学思想方法结构，呈螺旋上升的样态进行整体编排。对教师而言，读懂教材，不仅要把握教材的知识结构，还要关注其思想方法结构。

从小数的意义建构来看，教师作为教学设计者，需要将“小数的认识”置于数系的整体中进行观察与思考。整数、分数、小数的认识是“数与代数”领域的重要内容，是小学数学的基础与核心，而“小数的认识”在“数的认识”序列中又处于非常重要的位置。从数系的角度来看，小数与整数、分数有着非常密切的联系。从应用的维度来看，小数的应用在现实生活中比比皆是。从认知的层面来看，小数的学习对于培养学生的结构性思维和成长性思维大有裨益。

基于学生认知发展的阶段性特征，小学数学教材一般分两个阶段安排“小数的认识”：一是基于现实情境，初步认识小数；二是逐步概括抽象，进行意义建构。苏教版教材的编排如下：一是在三年级下册安排“小数的初步认识”，重视激活学生原有的认知经验，聚焦生活中的数学原型，在实践与探索中逐步建立数系关联；二是在五年级上册安排“小数的意义和性质”，就小数的意义建构而言，更为关注关系的可视化、认知的结构化和关联的系统化。

二、把握增值的前提：关注学生的认知基础

小学数学教学不仅要关注知识的来龙去脉和发生发展，还要聚焦学生的认知基础与学习规律，从知识的形成、发展线索和学生的认知线索这两个维度进行整体设计。从小数的意义建构来看，学生已经具有关于数的认识、计量单位的认识以及意义建构的模型认识这三大基础。

（一）学生关于数的认识的认知基础

小数与整数结构相似、关系密切，小数与十进分数也有着密不可分的联系。因此，学生关于整数、分数的认知基础对小数的学习而言至关重要。其一，在学习“小数的初步认识”之前，学生已经完成了万以内整数的认识，知道数位和计数单位，对“位值”和“十进制”有了比较充分的了解，在此基础上认识小数，能较为有效地进行正迁移。其二，学生在三年级上学期学习了“分数的初步认识”，知道将一个物体、一个计量单位平均分成10份，其中的一份就是这个物体、这个计量单位的十分之一，其中的几份就是这个物体、这个计量单位的十分之几。小数是十进分数的另外一种表达方式。因此，对于分母为10、100、1000……的分数的认识，为小数的认识提供了必要的结构支持。

（二）学生关于计量单位的认识基础

其一，学生对长度单位有一定的认识。学生在二年级已经完成了对厘米、分米、米的认识；知道测量长度时需要使用长度单位，了解米、分米、厘米之间的进率关系；具有一定的测量经验，知道有时不能得到整数的结果。其二，学生对人民币单位有一定的认识。学生了解元、角、分是人民币的单位，知道1元=10角和1角=10分，具有一定的购物付款的经验。无论是对长度单位的认识还是对人民币单位的认识，因其相邻两个单位之间的进率是10，与十进制有着紧密的关联，都为学生认识小数提供了结构化、形象化、情景化的经验素材库。

（三）学生关于意义建构的模型认识基础

从呱呱坠地开始，儿童就在生活中、学习中不断接触各种各样的数，并从生活中的数、情境中的数逐步抽象为数学中的数。在此过程中，从具象到表象再到抽象，逐步完成数学化思考的过程。

1.在多元表征中认数

对于数的认识，学生常常需要经历从丰富的现实情境中逐步提炼共性、抽象概括的过程。在形象与抽象之间，计数工具（如计数器、小棒、算盘等）发挥着重要的桥梁作用。如下图1所示的325的不同表达，无论外在的形式如何变化，计数的载体如何丰富，其数学核心都是表示出了3个百、2个十和5个一。在多元表征中引导学生关注共同特征，有助于他们实现从感性认识到理性认识的升华。

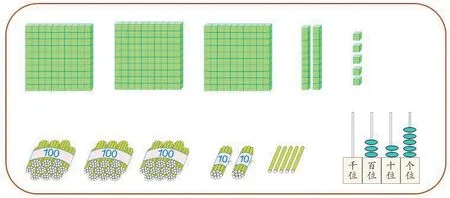
（图1）

2.在数形结合中认数

数与形是两个最基本的数学研究对象。在教学中，引导学生将直观的图形语言与抽象的数学语言建立起关联，往往可以起到事半功倍的教学效果。数形结合的思想方法也是数学教学中一条重要的思想主线。数学家华罗庚先生就曾用“数形结合百般好”来表达数形结合的价值与意义。

在整数、分数、小数的认识中，借助各种直观图形可以帮助学生更好地理解抽象的数的概念。下图2就是“千以内数的认识”中非常典型的数形结合的例子。学生可以借助点子图抽象出数，还可以在点子图与数线对照中感知数与图之间的对应关系。学生可以通过圆点的叠加感受数的增大，通过圆点的减少感受数的减小，并由此感受数轴上不同位置的数的大小关系。

（图2）

三、聚焦增值的关键：实现小数的意义建构

真实的学习，是学生基于原有的知识与经验基础，主动理解、建构意义的过程，是认知结构不断扩展并自我完善的过程。从数学认知结构的生长方式来看，一种是同化，另一种是顺应。教师应如何基于同化与顺应来引导学生建构小数的意义呢？

我们在心跳声中走上楼梯，走进她的卧室。床头上挂着一张她的全身照片，只穿着薄薄的纱衣，似法国画家笔下的天使。我回转头，发觉她本人比照片还要美。她已在我看照片时脱去了外衣。

（一）让经验可借鉴

没有一个学生是空着脑袋走进课堂的。每一位进入课堂的学生，或多或少都带着自己的生活经验与数学经验。基于这样的观点再来审视“小数的认识”，我们会发现：虽然数的本质是抽象的，但小数作为十进分数的另一种表示方式，在生活中应用十分广泛。同时，对学生而言，测量长度的结果不是整米数、物品的价格不是整元数……这些都是生活中常见的运用小数的现象。

1.基于测量经验进行设计

苏教版教材中“小数的初步认识”就是基于学生的测量经验进行设计与实施的：两位同学在测量课桌，发现桌面长5分米、宽4分米，如果用米作单位，不满1米，怎么表示呢？自然而然，激活了学生原有的生活经验与学习经验。不满1米时，可以把1米平均分成10份，5分米有这样的5份，就是十分之五米，还可以表示为0.5米。对学生而言，这样的情景化、任务型的挑战是站在新旧知识的链接点，实现数的认识的自主对接，完成认知结构的自我拓展。

2.基于购物经验进行设计

除了借助测量经验展开教学之外，还可以借助购物经验进行设计。对学生而言，超市中各种物品的价格大多是用小数表示的。虽然没有系统认识过小数，但对于生活中用小数表示的物品价格，学生都知道其具体意义为几元几角几分。因此，教师可以通过“唤醒生活经验—激活数学认知—发现意义关联—建构初步认识”这样的线索进行具体教学。创设“一个购物袋0.1元，需要付多少钱？”的问题情境，引导学生在一个代表1元的正方形中用自己的方式表示出0.1元。然后组织学生分析、比较其不同的表示方式，直观感知0.1元是1角，1角是1元的十分之一，也就是十分之一元，十分之一元还可以表示为0.1元。引导学生在自我创造与自我发现中，通过分一分、涂一涂、比一比、说一说等系列化的活动，建立起新数与旧数的联系，架构起小数与分数的桥梁，从而使他们从意义理解走向意义建构。

（二）让图式可应用

以数学符号、图形、关系图等为载体的数学图式兼具形象与抽象的特征。因此，在数的认识中，需要关注基于图式模型的设计，在形象与抽象之间形成增强回路。基于数学图式的教学设计，一方面需要基于学生已有的知识经验；另一方面需要指向学生思维生长的实践路线。

在“小数的初步认识”中，教师可以基于价格模型引导学生进行自主建构，形成0.1元的直观图式，并在此基础上认识0.2元、0.3元……在代表1元的正方形的十等分模型建构的基础上，借助动态变形，完成如下图3所示的从正方形图式到长方形图式再到类米尺直条的变化过程。在变化中聚焦不变，引导学生关注小数的本质，十分之几的分数可以改写为一位小数。进而在类米尺的直条中，从价格单位自然走向长度单位，再走向任意的其他计量单位，最终抽象为单位“1”，在“正方形图式→直条图式→线段图→数轴”（如图4）的过程中完成小数的整体建构。从具象的代表1元的正方形图式模型，逐步剥离现实意义到代表1的线段图式模型，并在此基础上抽象为数轴图式模型，结构化的设计、系统化的内容、成长型的思维让教学成为可延展、可持续、可迭代的过程。

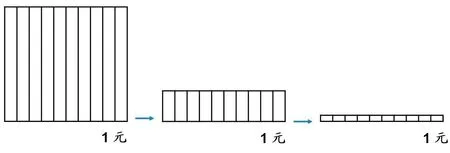
（图3）

（图4）

2.在关联中变化

在“小数的初步认识”中，借助测量经验，基于长度单位模型，可以较好地完成十进分数与小数的链接。在此基础上，如何实现长度单位模型与价格单位模型的有机对接，从而在丰富的生活原型中寻找共同的数学图式表达呢？下图5呈现的就是在认识与研究长度单位模型的基础上，教师引导学生从元与角的关系入手，从具体形象的1个1元硬币的价值与10个1角硬币的价值相等，逐步过渡到代表1元的长方形平均分成10份，进而抽象为单位线段的过程。在这样的关联中，我们感受到的是两种计量单位的生活模型在数学视域中实现了统整与归一。从以图为基、按图索骥到建立联结、族群化归，从可见的图式到可感的图式，从物化的表征到心理的图式，模型可见，学生的思维可见，生长亦可见。

（图5）

（三）让结构可迁移

好的数学教学善于找寻联结、找准关系、找到方法，以结构模型导引，实现正向迁移，从而使数学知识“像树一样生长”。引导学生从“前结构水平”走向“单点结构水平”，进而走向“多点结构水平”，再走向“关联结构水平”，最终走向“抽象拓展结构水平”。

1.基于直观进行结构性研究

对十进制计数法的认识以及对分数的初步理解是学习小数的两个重要基础。在第一学段学习“小数的初步认识”时，主要的研究载体是元、角、分和米、分米、厘米、毫米，这两类计量单位的共同特点是相邻两个单位间的进率都是10。因此，在研究小数的意义时，充分利用直观素材有助于学生进一步在小数的意义与十进制之间建立联系。各个版本的教材都充分运用“米尺”这一直观载体，引导学生借助测量的经验，基于对长度单位的认识，通过对刻度线的观察获得对小数的意义与十进制关系的直观性与结构化认识。下图6便为苏教版教材中“小数的意义和性质”的学习导引示意图。

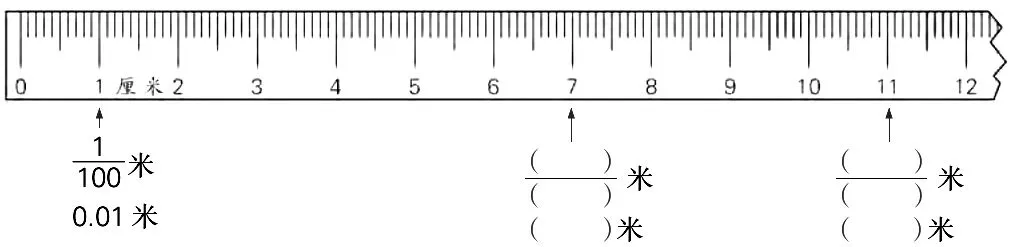
（图6）

2.基于经验进行结构性推理

学生在学习苏教版教材中“小数的初步认识”时，对十分之几可以表示为一位小数有了较为深刻的理解。在第二阶段探究小数的意义时，教师可以着力引导学生在“长度背景”中依次用“米”作单位的分数表示出几分米、几厘米和几毫米，并由“一位小数表示十分之几”类推出“两位小数表示百分之几，三位小数表示千分之几……”，充分发挥学生已有的生活经验、知识经验和方法经验在理解小数意义过程中的支撑作用，引导他们尝试基于经验进行合理推理。基于经验进行结构性推理，有助于学生在大量形象化、情景化的背景中进一步抽离与概括，形成对小数的意义的初步归纳，从而自主建构小数的意义。

3.基于图式进行结构性演绎

如果说基于情境逐步抽象、概括、归纳是数学建模的重要步骤，那么，基于图式进行解释、说明、演绎也是数学建模的重要方面。教学小数的意义时，怎样进行基于图式的结构性演绎呢？我们可以引导学生回忆学习“小数的初步认识”时基于对1元的认识而产生的0.7元的图式，进而给出比0.7大且比0.8小的小数的结构图式，引导学生想办法表示出涂色部分的大小。面对认知冲突，学生能够想到继续细分，将这一小格再分为十等份，相当于将整个图形平均分为100份，从而获得准确的数学表达——0.78。（如图7）解决了这一具有挑战性的问题，学生面对再增加一小块涂色部分时，就能以此类推，继续均分，从而获得0.782这个三位小数。这样的过程可复制、可持续、可迁移，有助于学生在“新冲突—再细分—新小数”的认知链中，从十分之几到千分之几，从一位小数到三位小数，从10-n到n位小数，实现对小数意义认识的逻辑自洽与结构再生。在这样的学习与研究过程中，从正方形模型均分与小数表达到正方体模型均分与小数表达（如图8），进而拓展为数轴模型的小数表达，如此，结构模型得以迁移，学生的认知模型得以拓展。

（图7）

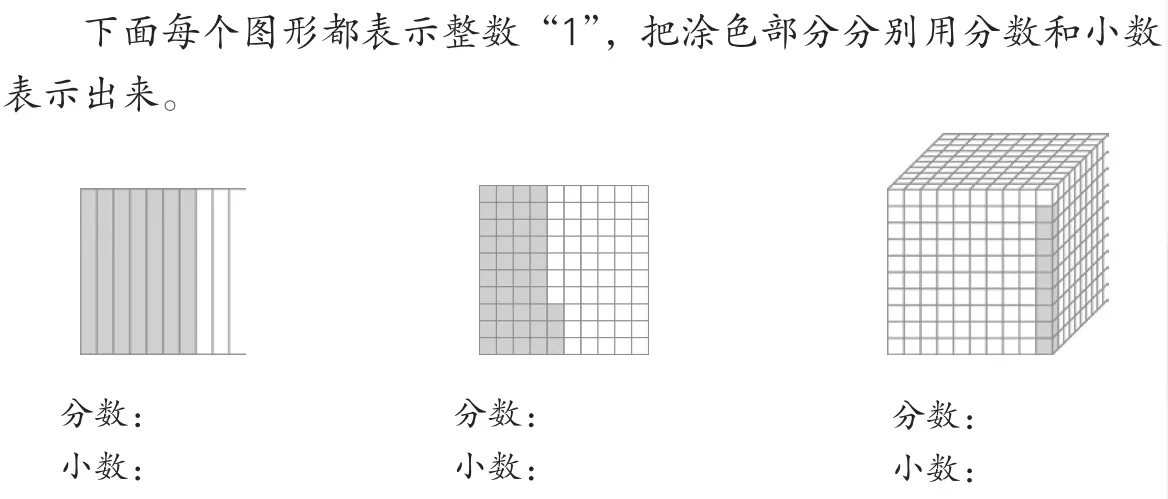
（图8）

综上所述，笔者认为，最好的设计，其实是最美的预见，更应是最美的遇见。有专业视野和专业解读，方能预见；有专业实践和专业坚守，方能遇见。在预见和遇见之中，教学的增值正在悄然发生。