“证作导找”解析垂直关系中的基本套路
2022-10-24邢富根
◎邢富根
(南京市高淳区淳辉高级中学,江苏 南京 211300)
垂直关系是立体几何中的难点问题,其中线面垂直在立体几何中的地位举足轻重,不但是位置关系的核心,而且是角度、距离等问题的关键垂直证明中的四个方向如何定位,怎样找到四个方向证明上的预判断,是学生突破垂直关系、提高解题速度的关键
垂直关系证明中,逆推是主要的方法逆推法又叫分析法,是从分析每一个结论的必要条件开始,步步倒推,直至说明题目给出的条件恰好符合要求为止逆推法实际上是把证明反过来了,但并不完全一样逆推法是一种很好的导向思维,它既可以训练学生的逻辑思维能力,又能很准确地辅助判断必要条件,在垂直关系的证明上,逆推法是主要的思考方法
对证明结论必要条件的逆推,本质上是建立在逆推基础上的一种辩证逻辑,是指导学生利用所学数学知识进行表述和论证,形成有论据、有条理、合乎逻辑的思维品质,增强数学交流能力的过程试题通过四个关键点的连接,在必备知识考查的基础上,增加综合性与应用性,提高学生关键能力,渗透学科素养
垂直关系证明的四个关键字:证、作、导、找
由线线垂直得到线面垂直的关键字是“证”线线垂直是证明线面垂直的主要方法,即证明一条直线垂直于平面里的两条相交直线学生通过找到垂线来完成线面垂直的证明而基础条件中的线线垂直,处理手段通常是两种情况:1在同一个平面内的可以考虑三线合一、勾股定理逆定理、相似三角形等办法,也可建立平面直角坐标系通过计算得出2不在同一平面内的线线证明一是通过“平行传递”回到第一种方法,二是通过线面垂直实现线线垂直的证明而通过线面垂直去证线线垂直的关键字是“导”所谓“导”,就是引导出两条线中,谁是垂线,垂直于另一条线过的哪一个平面定垂线是此类问题的难点所在而三垂线定理模型的应用,往往是寻找垂面最实用的办法以上线线垂直与线面垂直的互推,形成了逻辑严密的“垂直证据链”的基础条件
面面垂直往往是导向性条件,它的推导结论一定是线面垂直,要点是盯住交线,寻找交线的垂直条件,以快速找到面的垂线而在综合法解决线面角、二面角以及距离问题中,作出垂线(线面垂直)往往是形成平面角以及距离的通道那么如何形成垂线呢?除了我们通过线线垂直证明线面垂直以外,在面面垂直的条件下,在一个平面里作一条直线垂直于交线,则它一定垂直于另一个平面,所以,由面面垂直得到线面垂直的关键字是“作”
1如图1,在三棱台-中,平面⊥平面,∠=∠=45°,=2

图1
(1)证明:⊥;
(2)求直线与平面所成角的正弦值
思路分析:
本题(1)证明:⊥,从结论出发,逆向推理,由平行传递转化为证明⊥要证线线垂直,我们可考虑通过线面垂直来证明,由题目中的导向性条件平面⊥平面,易在平面中作的一条垂线,这样既垂直于又垂直于,所以转证垂直于平面,再转化为证明垂直于(本质上还是三垂线定理的模型)
本题(2)求直线与平面所成角的正弦值,综合法求解线面角问题的关键是找到垂线,而作出垂线的关键是找到垂面由(1)易知,平面的垂面是平面,故将通过平行传递给,而与平面正好相交于点,那么通过作⊥,即得到⊥平面,得到二面角的平面角
证明如下:
(1)如图2,过点作⊥,交直线于点,连接

图2

由平面⊥平面,得⊥平面,所以⊥

所以⊥平面,故⊥
由三棱台-得∥,所以⊥
(2)过点作⊥,交直线于点,连接
三棱台-中,∥,故直线与平面所成角等于直线与平面所成角
⊥平面得到⊥,⊥平面,所以∠为直线与平面所成角




在垂直关系中,最具有灵活性和挑战性的,还是面面垂直的证明由线面垂直得到面面垂直的关键字是“找”
根据面面垂直的判定定理,一个平面过另一个平面的垂线,则面面垂直,由此可知,要想完成面面垂直的证明,关键是找到线面垂直找到这条垂线,成了解决问题的入口,这也是垂直关系中的一个难点问题
那么,如何在给出的两个面里准确定位一条直线垂直于另外一个平面呢?我们常见的处理方法是:1观察法,观察两个平面中哪条直线的垂直条件多,这也是它能成为垂线的必要条件2“逆向思维”法,要证面面垂直,那么我们假设面面垂直,根据面面垂直的性质定理,如果一个平面内有一条直线垂直于交线,则它垂直于第二个平面我们把目标聚焦在交线上,垂直于交线的直线即我们要找的垂线,完成定位后,我们只要依靠线面垂直的判定定理,完成证明即可


图3

图4
思路分析:
方法1:我们发现在图4中,可以找到两垂面的交线,观察可知,⊥,所以必为垂线而完成⊥平面的证明,只要能证明分别垂直于、,用勾股定理逆定理即可得出
方法2:找到两垂面的交线,由三线合一可作⊥,必为垂线证明为垂线,应把主要目标放在证明⊥上,通过三角形中的边角量传递,由勾股定理逆定理即可得出
在垂线的找寻中,透过多垂直条件的综合判断来精准定位垂线,再用线线垂直加以证明,这是最主要的方法
所以,我们通过对垂直关系的整理,可以发现如下关系:
在线面垂直的证明中,证明直线垂直于平面内两条交线依然是主导方法而在作垂线的问题上,我们往往通过找到垂面以面面垂直的性质定理完成线面垂直的证明,而这更多应用于线面角、二面角(垂线法找角)以及距离问题的垂线定位
在面面垂直的证明中,找线法(找垂线)至关重要而在线线垂直的证明中,三垂线定理的导向性在较复杂的模型中,对寻找垂面起决定性作用
掌握这些关键词,我们更容易找到我们所需的必要条件,在问题证明上将更加具有方向性,形成预判,快速找到证明的路径,提高解题速度,并有效拓展逻辑思维能力,提升学生数学素养
下面我们以综合性的距离问题、动态开放性问题为例,赏析解剖综合法应用中垂直关系的关键点
3如图5,四边形是边长为2的正方形,△为等腰三角形,=,平面⊥平面,点在上,且⊥平面

图5
(1)求证:平面⊥平面;
(2)求点到平面的距离
思路分析:判断哪条直线可能是垂线
鉴于⊥平面的条件,的垂直条件更多,易得出:
⊥且⊥,故⊥平面,得面面垂直
证明如下:
(1)因为⊥平面,且⊂平面,所以⊥
因为平面⊥平面,直线⊥,
平面∩平面=,⊂平面,
所以⊥平面,又⊂平面,从而⊥
因为∩=,,⊂平面,所以⊥平面,
又因为⊂平面,故平面⊥平面
步骤:“一找二证三求”,即①找出或作出有关的距离;②证明它符合定义;③归结到某个三角形中计算求出三步都必须清楚地写出来
垂线的找法分析:到平面的距离,需要找到过且与平面垂直的平面,显然面不是垂面,因为假设面是垂面,那么根据面面垂直的性质定理,⊥平面,进而⊥,而又有⊥,按此逻辑⊥平面,显然矛盾同理,面,面都不可能是垂面,故由作垂线的路径困难此时思考替代点,等距替代点到面的距离即要求的到平面的距离,而此时不管是垂面(平面)还是已知条件中的垂线,都易知是目标距离
(2)如图6,连接交于点,则点是的中点,

图6
所以点与点到面的距离相等
因为⊥平面,所以的长为点到平面的距离
又因为⊥平面,⊂平面,所以⊥
因为=,所以△是等腰直角三角形




点评:评估是否垂直,用逆向思维的方法进行排除,也是基于证、作、导、找的技术推进,进行假设性的否定,以更加准确地判断目标垂直关系


图7
(1)求证:⊥平面

思路分析:
(1)求⊥平面是个基础问题,证明垂直于两条相交直线即可;分析可知与在同一平面中,利用相似三角形可推导出垂直关系要证⊥(线线垂直),考虑线面垂直,逻辑上只能证明垂直于所在的平面,即平面,易证
(2)面面垂直的关键点是找垂线,一定一动的垂线找法会更加容易只要找准定面的一条垂线,平移至动平面(与动平面中的定直线相交生成动平面)在本题中是平面的垂线,沿方向平移至与相交形成垂面
证明如下:
(1)因为-是直棱柱,又⊥底面,⊂平面,
所以⊥
又因为是棱的中点,=,所以⊥
因为∩=,,⊂平面,
故⊥平面,
又因为⊂平面,所以⊥
=2,所以=1


即∠+∠=∠+∠=90°,
所以⊥(平面化的垂直证法)
因为∩=,,⊂平面,
所以⊥平面

如图8,取的中点,连接、
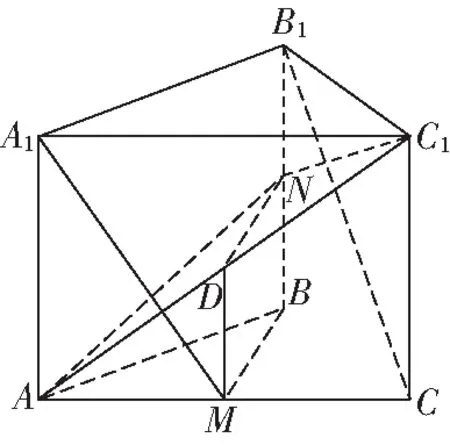
图8
因为、分别为、的中点,

又因为为的中点,

∥,所以∥,且=,
所以四边形为平行四边形,所以∥
因为⊥平面,
所以⊥平面
又因为⊂平面,
所以平面⊥平面
点评:垂直的动态问题,往往更加具有导向性,面面垂直的关键在于找到面的垂线,而线线垂直证明的方法主要基于线面垂直(或者三垂线定理),在同平面内垂直的证法,更多利用相似、三线合一、勾股定理逆定理、坐标系算法(利用解析几何或者平面向量的垂直关系)等
垂直体系是综合法解决立体几何的重要知识链,也是实现思维逻辑性发展的重要载体教师教学中要运用知识网络深挖各种信息,利用稳定 “模型”,寻找关键节点,探索解题思路及方法教师的教学要点是呈现思维层次,把多元信息融合,带领学生找到关键点,例如垂直关系,各个方向的证明点都有导向性条件教师引导学生建立深层的垂直逻辑关联,可以提高他们解决数学综合问题的能力
