近断层地震动下可更换构件铁路高墩易损性分析

高泽亮，夏修身，黄耀斌，钟亚伟，戴胜勇

(1. 兰州交通大学 土木工程学院，甘肃 兰州 730070；2. 中铁二院工程集团有限责任公司，四川 成都 610031)

传统高墩基于延性设计理念，通过塑性变形耗散地震能量，震后结构所产生的损伤和残余位移难以修复，致使其丧失使用功能[1-2]。例如，阪神地震后100余座桥墩因墩柱倾斜超过1°，修复困难而拆除重建，对当地经济发展带来巨大损失[3]。随着震后无损伤结构设计理念的提出，摇摆及自复位桥墩受到了较多关注。摇摆及自复位桥墩利用地震中桥墩的摇摆过滤地震动能量并通过结构自重来自复位，在避免墩底形成塑性铰的同时还有效减小了桥梁震后残余位移[4]。但自复位高墩受高阶振型影响显著，仍会在结构中部区域形成塑性铰，给桥墩的抗震设计带来难题[5-6]。基于震后使用功能可快速恢复理念[7-9]，XIA等[10]提出一种新型可更换构件铁路高墩结构，该新型高墩可通过可更换杆件集中耗散地震能量，从而使主体墩柱结构低损伤或无损伤。马朗[11]研究了可更换构件在3 条地震动激励下的损伤演化，探讨了可更换构件截面面积变化对墩柱内力的影响规律，但分析中假定墩柱始终处于弹性状态。黄耀斌[12]研究了新型高墩在3条地震动作用下墩柱损伤演化规律，结果表明可更换构件可以显著抑制墩柱塑性区的范围。在上述研究基础之上，本文建立全桥非线性动力分析模型，为充分考虑地震动不确定性因素，沿横桥向输入294 条地震波进行增量动力分析(IDA)，考察可更换构件高墩结构的弹塑性演化过程，采用易损性方法探讨新型高墩中可更换杆件的损伤超越概率分布规律，并从概率角度对可更换构件高墩结构进行抗震性能评估。

1 新型铁路高墩结构及有限元模型

1.1 工程背景

以某铁路预应力混凝土连续刚构桥为工程背景，其5号桥墩为柱-板式桥墩，墩高为105 m，见图1。根据自振周期等效的原则，新型高墩用钢桁架连梁替换原5号主墩墩柱之间连接的薄壁板和横梁，见图2。新型高墩中布设了7 排钢桁架连梁，直线段与曲线段的钢桁架连梁间距分别为10 m 与7.5 m，其杆件的截面尺寸示于图3。

可更换构件新型高墩主要由4根墩柱及墩柱之间的钢桁架杆件组成，见图4。墩柱位于截面的四角，是新型高墩的主要构件，采用钢筋混凝土材料。钢桁架连梁杆件为次要构件，其功能为使4个墩柱形成一个整体，提供初始刚度，以保证铁路行车舒适。小震作用下处于弹性状态、强震作用下次要构件为耗能构件，震后其可更换或可修复。

1.2 动力分析模型

基于OpenSees 平台建立全桥动力分析模型，模型共有501 个节点，主梁采用132 个弹性梁柱单元模拟，5 号主墩的4 个墩柱及其之间的可更换杆件共有386个单元，均采用基于柔度法的纤维梁柱单元模拟[13]。钢筋与混凝土材料分别采用steel01和concrete01 本构模型。主梁与3 号及7 号边墩为活动约束、采用EqualDOF command 模拟，主梁与4号，5号和6号墩为刚构连接、采用RigidLink command模拟。不考虑桩-土作用、墩底均采用固结。

2 IDA分析

本文重点探讨可更换杆件的损伤状态。由于同排、同类型的构件地震响应相近，文中分别选取每排构件中的一根斜腹杆与一根弦杆进行分析。可更换杆件从上向下分别为第1 排～第7 排，其弦杆依次按C1～C7 编号，腹杆中的斜腹杆依次按W1～W7 编号，腹杆中的竖杆依次按V1～V4 编号。参考文献[14]，选取峰值加速度(PGA)作为地震动强度指标，可更换杆件材料应变作为损伤指标。

2.1 地震动输入

根据文献[15]的研究，IDA分析中采用20条地震动记录作为输入可反映地震动的不确定性。鉴于近断层地震动较容易激发高墩的高阶振型效应[16-18]，从美国太平洋地震研究中心强震记录数据库，选取21 条震中距为2.5～14.7 km，PGA/PGV为0.8～1.2之间的近断层地震动。21条地震动记录的加速度反应谱见图5。IDA 分析时将21条地震动记录进行调幅，每条地震波由0.1g调幅到1.2g，步长为0.1g，并在9 度各设防水准下进行专门调幅，得到了294条地震动。沿横桥向输入，进行非线性时程反应分析。

2.2 IDA分析结果

可更换构件在PGA 为0.5g时第4 排斜腹杆开始屈服，在PGA 为1.1g时7 排斜腹杆全部屈服，屈服顺序为第4，5，3，1，6，2，7。可更换构件中斜腹杆的地震响应远大于竖杆及弦杆，这是因为弦杆地震应力主要由墩柱相对位移引起，而在地震作用下墩柱间的相对位移较小，所以弦杆所受应力较小，而斜腹杆应力主要由墩柱之间的剪力所致。

由于各排IDA 曲线形状相近，典型的IDA 曲线如图6所示。

由图6(a)和6(b)可知，斜腹杆单条IDA 曲线有明显的屈服拐点，曲线簇则呈现出一定的离散性，并且弹性阶段的离散性明显小于塑性阶段，其中离散性由上排至下排有逐渐减小的趋势，说明在塑性阶段，上排斜腹杆对地震动强度变化较下排更加敏感。由图6(c)可知,腹杆中的竖杆处于弹性状态，故本文不对其进行易损性分析。由6(d)可知，弦杆单条IDA 曲线基本呈线性变化，曲线簇离散性相对较小，最大应变值远小于屈服应变，说明弦杆处于弹性状态。

3 可更换构件易损性分析

3.1 地震需求概率模型

地震易损性曲线可以通过经验分析方法和理论分析方法获得[19-20]，其中理论易损性分析方法中能力需求比模型的非线性拟合法比线性拟合法更加精确，本文选用能力需求比模型的非线性拟合法，其计算公式如下[21]：

式中：Pf为结构达到对应极限状态的超越概率；Sd.为结构对应极限状态的地震反应需求；Sc为结构对应极限状态的抗震能力；λ为结构达到极限状态的需求能力比对数回归均值；σ为标准差；a，b，c为回归系数；Sr为各离散点对于回归曲线的残差平方和；n为离散点个数。

3.2 损伤指标与极限状态

为了评估可更换杆件的抗震性能，需要在易损性曲线上定义杆件各种性能水平的极限状态。参考相关文献[22-23]，以应变为量化指标，定义斜腹杆及弦杆极限状态列于表1。

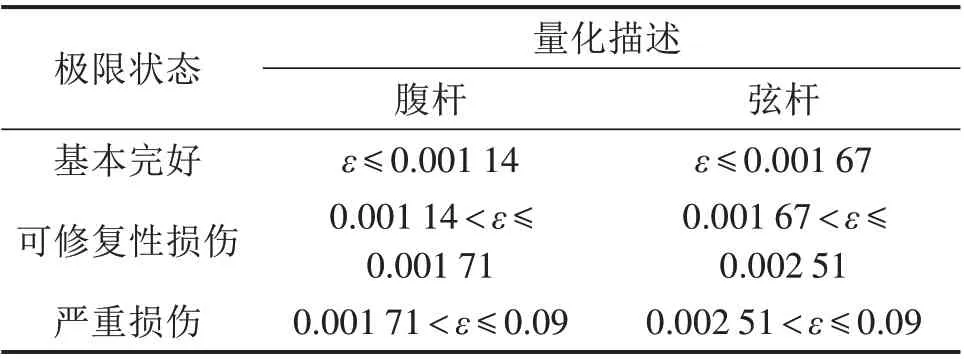
表1 极限状态定义Table 1 Definition of limit state

3.3 地震易损伤曲线

运用最小二乘法对IDA 曲线进行回归分析，得到λ的拟合回归系数a，b，c(列于表2)，再结合式(1)与式(3)计算各极限状态下弦杆及斜腹杆的损伤超越概率，列于表3。以PGA为自变量的易损性曲线见图7和图8。

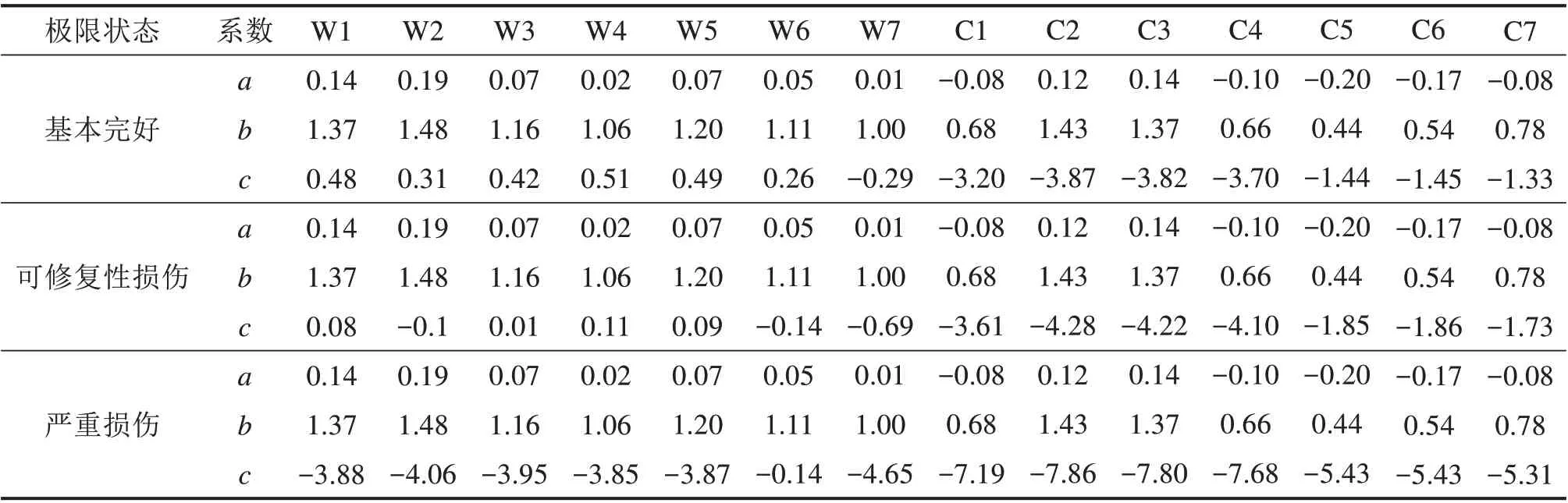
表2 回归系数Table 2 Regression coefficient

表3 可更换构件损伤超越概率Table 3 Damage exceeding probability of replaceable components

文献[24]结合第5代《中国地震动区划图》，提出地震可恢复功能结构“小震及中震不坏，大震可修复、可更换，巨震不倒塌”的四水准抗震设防目标。其中第四水准数值参考隔震规范(征求意见稿)中的地震系数k计算得到[25]。本文将第四水准(极罕遇地震动)定义为9 度巨震，近似取PGA 为1.2g，并对设计地震、罕遇地震及巨震下可更换构件的地震损伤状态进行评估。

由图7(a)可知W1，W3，W4 与W5 斜腹杆的易损性曲线较为接近，在PGA 为0.4g时，其损伤超越概率均在10%以下，在PGA 为0.6g时，其损伤超越概率均在50%以下，在PGA 为1.2g时，其损伤超越概率均在90%以上；W2 与W6 斜腹杆的易损性曲线较为接近，在PGA 为0.4g时，其损伤超越概率趋于0，在PGA为0.6g时，其损伤超越概率均在20%以下，在PGA 为1.2g时，其损伤超越概率均在90%以上；W7 斜腹杆的易损性曲线明显远离其他斜腹杆，在PGA 为0.4g与0.6g时，其损伤超越概率趋于0，在PGA为1.2g时，其损伤超越概率低于40%。由图7(b)可知，W1，W3，W4 与W5 斜腹杆在PGA 为0.4g时损伤超越概率趋于0，PGA 为0.6g损伤超越概率低于10%，PGA 为1.2g损伤超越概率均在80%以上；W2 与W6 斜腹杆在PGA为0.4g与0.6g时损伤超越概率趋于0，在PGA为1.2g时，损伤超越概率在50%以上；W7随PGA增大损伤超越概率变化不大，PGA 为1.2g时，其损伤超越概率小于5%。由图7(c)及图8可知，斜腹杆处于严重损伤状态和弦杆处于各极限状态的损伤超越概率均为0。

由表3 可知，在9 度设计地震PGA 为0.4g时，各排斜腹杆处于基本完好或可修复性损伤状态的超越损伤概率均少于7%，各排斜腹杆大概率处于弹性状态；在9度罕遇地震PGA为0.64g时，W2～W6 排斜腹杆处于基本完好和可修复性损伤状态的超越概率范围分别为17.6%～56.5% 与1.7%～10.5%，概率分布为W4 最大，依次向两端减小，W2～W6 斜腹杆处于弹性状态概率依然较大；在9度巨震作用下，W2～W6 处于基本完好状态的超越概率均在90%以上，处于可修复性损伤状态的超越概率在58%以上，W2～W6 排斜腹杆处于严重损伤的概率较大。W1 在罕遇地震后超越概率变化速率大，在9度巨震作用下处于基本完好和可修复性损伤的超越概率分别为99.4%与87.3%，为7排中最大。W7 在巨震下处于基本完好和可修复性损伤的超越概率分别为35.8%与3.6%，为7排中最小。C1～C7 弦杆在巨震作用下处于基本完好状态的超越概率趋于0，处于弹性状态。

9 度罕遇地震下墩柱中部区域斜腹杆W3～W5处于基本完好状态的超越概率明显大于其他位置的斜腹杆，原因在于墩柱中部区域的内力受高阶振型的影响相对较大。

墩柱在9 度罕遇地震下处于弹性状态，在9 度巨震作用下，大概率处于可修复性损伤状态，发生严重损伤状态的概率极小。限于篇幅，分析结果不具体列出。

4 结论

1) 墩柱中部区域W4 与W5 斜腹杆在9 度罕遇地震下超越基本完好状态的概率分别为56.5%和46.4%，处于可修复性损伤状态的概率较大，9 度巨震下超越可修复性损伤状态的概率均大于83%，大概率处于严重损伤状态。

2) 墩顶附近的W1 斜腹杆在9 度巨震作用下超越可修复性损伤状态的概率为87.3%，发生严重损伤的概率最大。

3) 墩底附近的W7斜腹杆较其他排斜腹杆在各极限状态下的超越损伤概率最小，9 度巨震作用下处于可修复性损伤的超越概率为3.6%。

4) 在9 度罕遇地震下，墩柱中部区域斜腹杆W3～W5 处于基本完好状态的超越概率明显大于其他位置的斜腹杆。

5) 在9 度巨震作用下，弦杆C1～C7 处于基本完好状态的超越概率为0，弦杆处于弹性状态。