PoP 元件热翘曲数值模拟及优化研究

葛一铭 ,徐 琴 ,曹 鹏 ,沈 飞 ,柯燎亮

(1.天津大学 机械工程学院,天津 300072;2.成都宏科电子科技有限公司,四川 成都 610100;3.中国航天标准化与产品保证研究院,北京 100071)

叠层封装(Package on Package,PoP) 技术将内部经过完整测试的封装模块堆叠到另一个经过完整测试的封装模块上部。采用PoP 结构的元器件因具有集成度高、小型化、轻量化等一系列优点,已经在航天、汽车和通信等领域得到了广泛的应用[1]。

尽管PoP 技术凭借其特有优势广泛应用于各个领域,但也正因为其具有多层互连结构,使得其在生产、服役等环节中出现了较多的失效问题,其中翘曲是一种常见的失效形式。叠层封装作为一种多层板结构,各层材料热膨胀系数的不同会导致热变形的失配,从而产生了机械应力和翘曲[2-3]。翘曲直接影响到封装体的共面度,过大的翘曲会使得结构在表面焊接组装过程中焊球无法连接,出现开路、短连及应力损伤。当芯片由于翘曲所引发的层间拉伸力大于层间粘结力时,会导致芯片脱层、剥离。芯片一般由硅制成,是一种脆性材料,当翘曲引发的弯曲应力大于其弯曲强度极限时,将造成芯片开裂,进而破坏其内部逻辑结构,造成性能失效,最终导致整个电子产品或设备发生故障[4]。对于大多数引线键合芯片,若裂纹扩展至焊点,还可能导致焊点开裂、偏移、脱焊等失效[5-6]。

国内外学者应用仿真技术针对元器件的翘曲现象进行了大量研究。Kang[7]采用参数化有限元分析的方法,评估了塑料球栅阵列封装的焊球间距、封装尺寸、塑封料和衬底厚度对其翘曲的影响。Qin 等[8]采用生死单元技术和重启动技术,研究了晶圆级和条带级封装的几何参数和材料参数对最大翘曲值的影响。Cheng 等[9]提出了一种将热-机械有限元分析、有效建模和生死单元技术相结合的过程仿真框架,有效地预测了芯片的翘曲。Cho 等[10]采用有限元分析和Taguchi 方法进行参数设计,通过寻找最佳厚度来减少PoP 双面基板中两个无源器件的翘曲。

结构翘曲的实验研究主要观测由于翘曲引起的结构离面位移,目前使用较多的方法有三维数字图像相关方法、阴影云纹法、白光干涉法等。Tsai 等[11]提出了一种与梁模型理论相关的简单易用的应变仪测量封装翘曲的方法,并通过有限元及阴影莫尔纹实验证明了该方法的可行性。Lall 等[12]使用三维数字图像相关方法测量了PoP 组件的翘曲,并与有限元仿真结果进行了对比。Kang 等[13]开发了一种动态数字条纹投影技术,用于测量塑料球栅阵列封装和电路板的翘曲。

本文建立了系统级封装中PoP 模块芯片热翘曲仿真模型,基于有限元方法实现了PoP 热翘曲的热力耦合仿真。在模型中考虑了锡铅焊料黏塑性的影响,计算了各芯片的翘曲度,分析了填充胶的热膨胀系数、芯片厚度及焊球弹性模量对芯片热翘曲的影响。研究结果可为PoP 叠层结构的热翘曲控制和优化提供理论依据,对封装的可靠性设计具有工程指导意义。

1 理论基础

1.1 热传导方程

在不考虑外部热源激励的情况下,均匀材料的瞬态热传导问题的控制方程为:

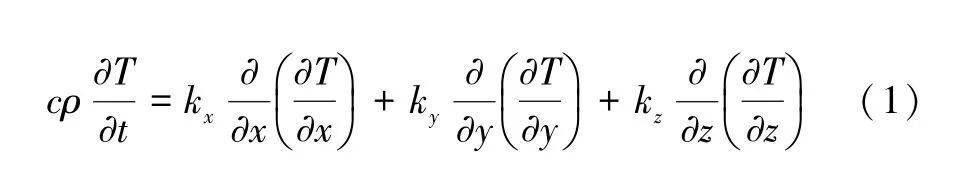
式中:T为温度;kx、ky、kz分别为x、y、z方向的导热系数;c和ρ分别为材料的比热容和密度;t为时间。

在典型的PoP 封装结构中,基板材料一般选用各向异性的FR4 材料,考虑材料物理性质随时间产生变化的情况,将式(1)推广至各向异性的夹层结构,热传导理论的微分方程变为[14]:

式中: [K]表示热传导系数矩阵;∇表示对空间坐标的梯度算子向量,其表达式如下:

根据复合材料的热力学理论,如果材料为各向异性,那么[K]为对称矩阵;若材料为正交各向异性,则[K]为对角矩阵;对于常规分析各向同性材料,[K]可直接写为常量矩阵。

1.2 热弹性本构关系

根据线性热应力理论,热弹性本构关系可以写为:

式中:i,j,k=1,2,3;εij为应变张量;σij为应力张量;α为线膨胀系数;ΔT为温度变化量;δij为克罗内克符号;λ和μ为拉梅常数,满足:

式中:G和ν分别表示材料的剪切模量和泊松比。应力张量可表示为:

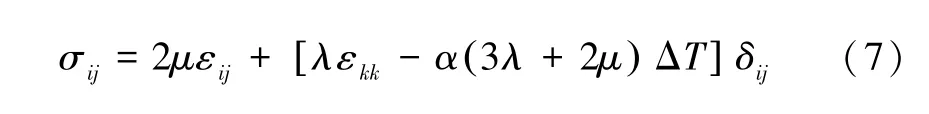
1.3 翘曲的计算方法

翘曲一般指整个组件弯曲时板中心和边缘的高度差,双层结构在温度变化时的翘曲值ω可以使用式(8)进行预测[15]:

式中: Δα为两种材料膨胀系数之差;L为板长;t1、t2分别为两板的厚度;E1、E2分别为两板的弹性模量。式(8)一般适用于粘结材料厚度远小于芯片和基板厚度时板上芯片组件翘曲的近似估计。

翘曲度是工程上常用的翘曲量度,在《QJ831B-2011 航天用多层印制电路板通用规范》 中明确规定了表面安装或混合安装用多层板的弓曲和扭曲应不大于0.75%。在计算翘曲度时,依照《IPC-T-50》,翘曲可分为弓曲和扭曲。弓曲是指板以圆柱形状或球面曲线形状偏离平面,扭曲是指平行于长方形对角线的板材变形,即一个角与其他三个角不在同一平面上。在仿真中,板四个角点的位移不一定相同,在计算翘曲度时,可采用简化的方法分别计算弓曲度和扭曲度。基于仿真结果,采用简化方法计算弓曲度ω1的公式为:

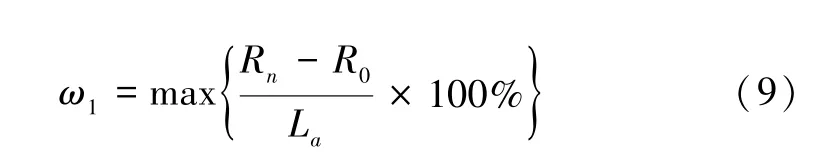
式中:n=1,2,3,4;Rn表示板4 个角点变形后纵坐标;R0表示板变形后最高点纵坐标;La表示板长边长度。

同时,采用简化的方法计算扭曲度ω2的公式如下:

式中:S表示矩形板的对角线长度;d为翘起的角距基准平面的距离。

2 有限元模型

本文以某系统级封装中PoP 模块作为研究案例,如图1(a)所示,该模块将两块相同尺寸的基板堆叠组装,通过侧面互连实现基板间信号传递。首先,将基板需引出的信号延伸到功能区外侧,将两个基板进行垂直堆叠,环氧灌封;然后,将堆叠体进行侧面切割,切割表面金属化,金属化层表面激光刻线;最终通过堆叠体侧面的立体互连实现将上下两个基板集成封装。其中,上层基板含有4 枚芯片,下层基板含有1 枚芯片,芯片均采用BGA 封装。基于上述互连结构,在承受外载时,侧边激光刻蚀区面积占比较小,大部分载荷由中部灌封区分担,因此对基板互连结构进行以下简化: 略去金属化层激光刻蚀区,同时忽略模块内电容及其他尺寸较小的元器件,将模型主体简化为基板与灌封胶的夹层结构。模块内部结构及相关尺寸如图1(b)和表1 所示。

表1 PoP 模块封装规格Tab.1 Packaging specifications of PoP module

图1 PoP 模块几何模型。(a)整体结构;(b)内部结构Fig.1 Geometrical model of PoP module.(a) Overall structure;(b) Internal structure

模型内各接触部位均采用绑定接触,经网格收敛性计算后,模块网格模型如图2 所示。其中灌封胶区域采用SOLID187 单元,其余部分均选用SOLID186 单元,在分析中对底部PCB 测试板施加固定约束,模块外表面承受温度变化,对流换热系数设置为25 W·(m2·℃)-1。温度加载曲线如图3 所示,加载时间为1320 s,温度变化范围为-55～125 ℃。在材料参数设置方面,芯片材料为正交各向异性硅,弹性常数矩阵为

图2 PoP 模块网格模型Fig.2 Grid model of PoP module

图3 温度加载曲线Fig.3 Curve of temperature loading

基板材料为FR4,密度为1500 kg/m3,比热容为880 J·(kg·℃)-1,FR4 的各向异性参数见表2,芯片、灌封胶、焊球(Pb90Sn10)及PCB 板材料参数见表3。

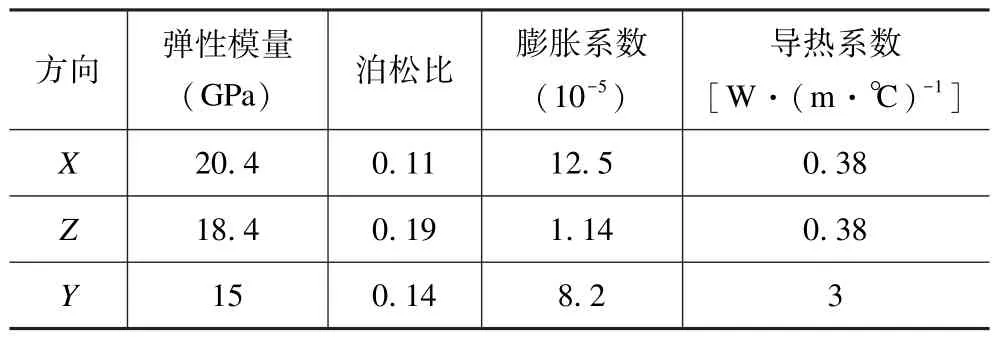
表2 FR4 各向异性参数Tab.2 Anisotropic parameters of FR4

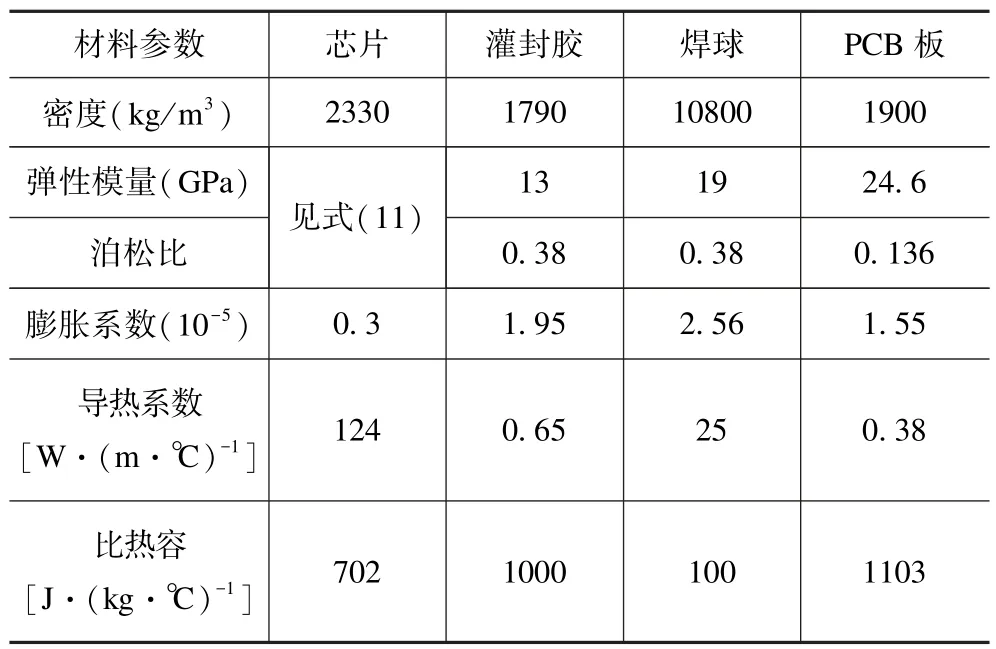
表3 模型材料参数Tab.3 Material parameters of the model

3 结果分析

3.1 PoP 热翘曲结果

SnPb 钎料在高温下往往表现出黏塑性行为,一般用Anand 黏塑性本构方程描述。Anand 黏塑性本构的基本特征是: 在应力空间没有明显的屈服面,在变形过程中,不需要加载和卸载准则,塑性变形在所有非零条件下产生,采用单一内部变量描述材料内部状态对塑性流动的阻抗[16]。为探究仿真过程中材料本构关系对结果的影响,对焊球材料分别采用Anand 黏塑性本构模型和理想弹塑性模型,其他部位的材料均采用弹性本构。两种本构模型的应力危险点均出现在芯片角点位置的焊球,图4 对比了分别采用理想弹塑性和黏塑性本构模型时该焊球最大Von-Mises 应力的变化情况。可以看出黏塑性本构模型的Von-Mises 应力远小于理想弹塑性模型,这同样也会导致两种模型计算得到的翘曲差别很大。由于结构的最大翘曲往往发生在温度较高时,而高温环境下材料黏塑性的影响必须考虑进去,因而后续的算例中焊球部分均采用黏塑性本构模型。

图4 不同本构模型下焊球的最大Von-Mises应力仿真结果Fig.4 Maximum Von-Mises stress simulation results of solder balls with different constitutive models

将PoP 模块置于PCB 测试板上,在1320 s 内,对器件施加-55～125 ℃的温度载荷,各芯片最高温度如图5 所示。可以看出D1 芯片温度最高(116.4 ℃),D5 芯片温度相对较低(107.2 ℃)。图6 给出了模块在125 ℃稳定阶段的整体变形,可以看出与芯片相比,基板四边和角发生翘曲更大。在高温稳定阶段,PoP模块内各芯片最大翘曲度见表4。扭曲度非常小可以忽略不计,模块内芯片的翘曲主要表现为弓曲,D2 芯片弓曲度最大,达到0.22%,各芯片翘曲度均未超出容许范围。

图5 各芯片的最大温度Fig.5 Maximum temperature of each chip

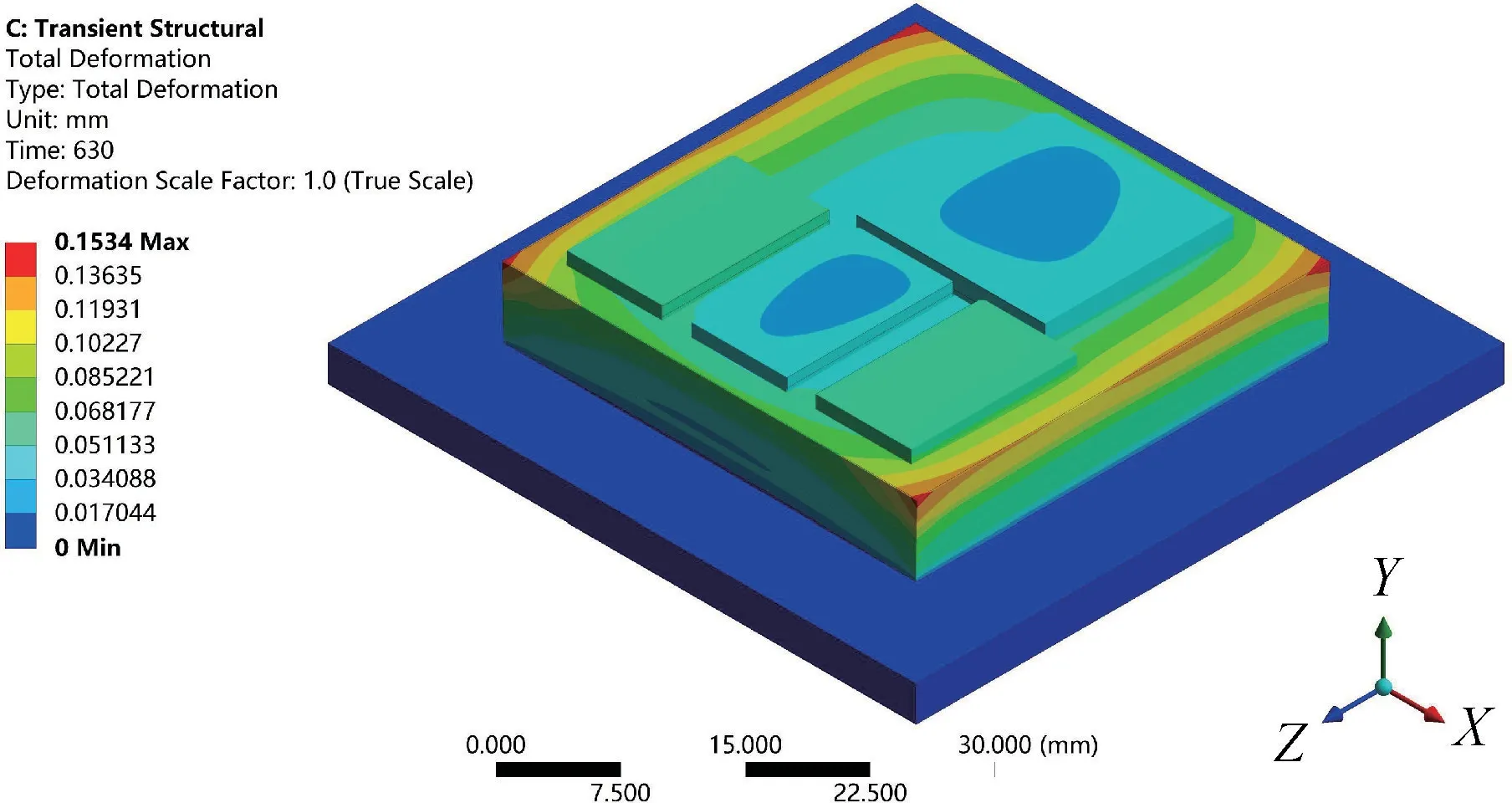
图6 PoP 模块最大变形云图Fig.6 Maximum deformation contour of the PoP module

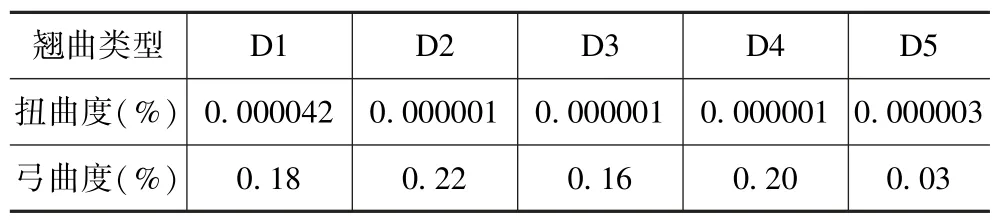
表4 各芯片翘曲度Tab.4 Warping degree of each chip

3.2 不同因素对热翘曲的影响

图7 研究了灌封胶热膨胀系数对芯片翘曲的影响。图7(a)给出了灌封胶热膨胀系数分别为1.95×10-5,1.65×10-5和1.35×10-5时,D1 芯片翘曲度随时间的变化。可以看出灌封胶热膨胀系数对翘曲度的影响较大,在高温和低温阶段D1 芯片最大翘曲度分别约为0.18%和-0.13%。在从高温到低温变化过程中,芯片翘曲形态由上凸形转变为下凹形。图7(b)讨论了各芯片最大翘曲度与热膨胀系数的关系。随着填充胶热膨胀系数的降低,各芯片最大翘曲度都呈下降趋势。D5芯片位于下层基板,并通过灌封胶完全包裹于模块中,翘曲并不明显。因此针对该PoP 模块,可通过选用热膨胀系数较小的灌封胶来减轻芯片的热翘曲。

图7 灌封胶热膨胀系数对芯片翘曲的影响。(a)D1 芯片翘曲度;(b)各芯片最大翘曲度Fig.7 Influence of thermal expansion coefficient of potting on chip warpage.(a) Warping degree of D1 chip;(b) Maximum warping degree of each chip

图8 讨论了芯片厚度对翘曲的影响,图中hm表示4 枚芯片的厚度,m=1,2,3,4。图8(a)考虑了芯片D1 在不同厚度时其翘曲度随着时间的变化。可以看出在高温区和低温区都发生了较大的翘曲,最大翘曲度发生在高温区,并且随着厚度增加而明显减小。图8(b)分析了芯片厚度对上层封装的4 枚芯片(D1～D4)最大翘曲度的影响。当其中一块芯片厚度变化时,其他芯片厚度假设不变。可以看出厚度对翘曲的影响是单调的,无论在高温区还是低温区,各芯片最大翘曲度均随其厚度的增加而减小。对于系统级封装组件,在面内往往有多个芯片集成,翘曲对芯片大小非常敏感,在设计时必须对芯片厚度进行优化[17]。

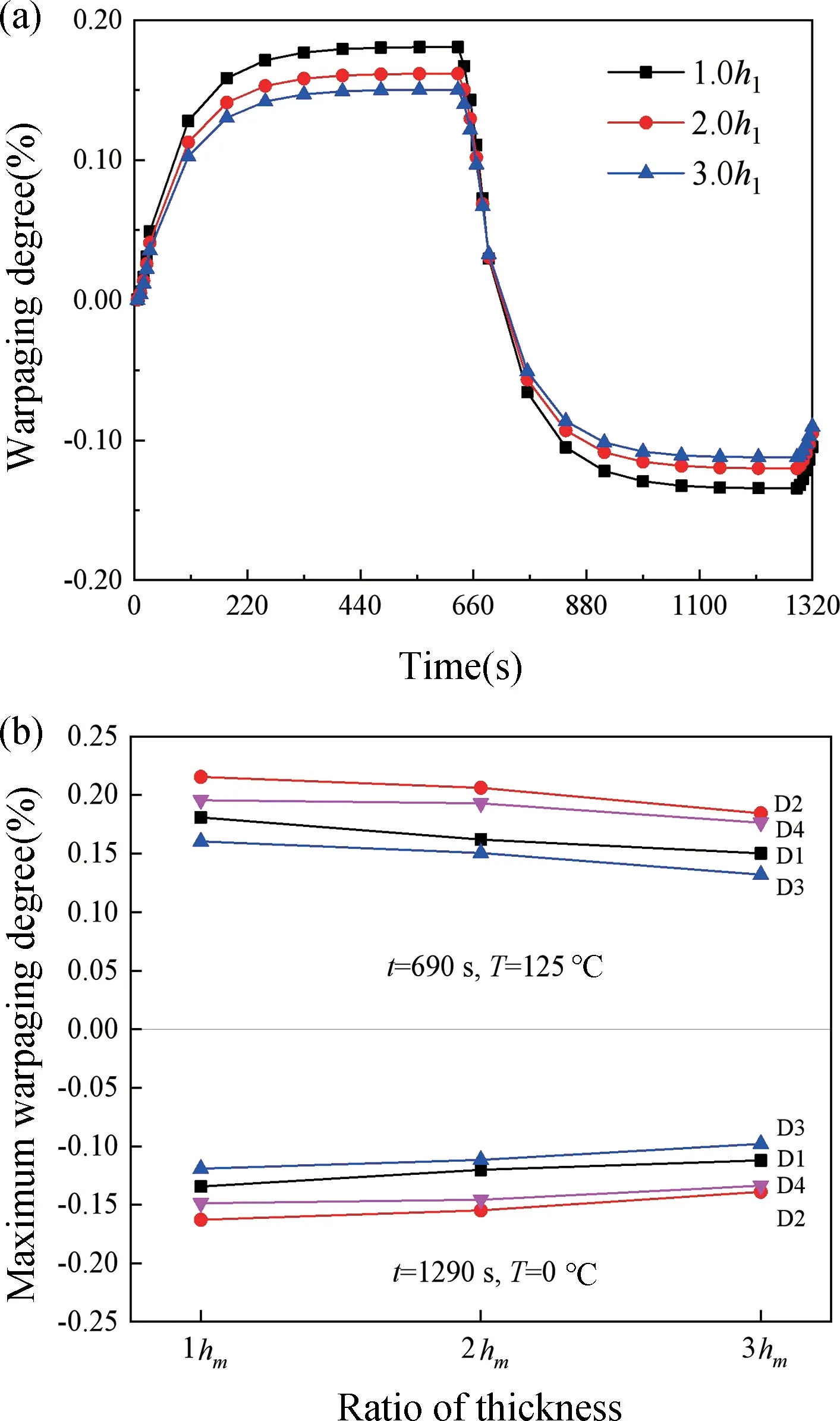
图8 芯片厚度对翘曲的影响。(a) D1 芯片在不同厚度下的翘曲度;(b)各芯片最大翘曲度Fig.8 Influence of chip thickness on chip warpage.(a) Warping degree of D1 chip with different thicknesses;(b) Maximum warping degree of each chip

图9 研究了焊球弹性模量对芯片最大翘曲度的影响。焊球弹性模量变化对芯片翘曲度的影响并不明显,这是由于组件的最大翘曲往往在高温区域产生,而受材料的本构关系的影响,在高温阶段焊料区域已产生较明显的黏塑性行为,此时焊球弹性模量变化对结构变形的影响进一步被缩小。因此,焊球弹性模量变化对PoP 组件翘曲度的影响较小。

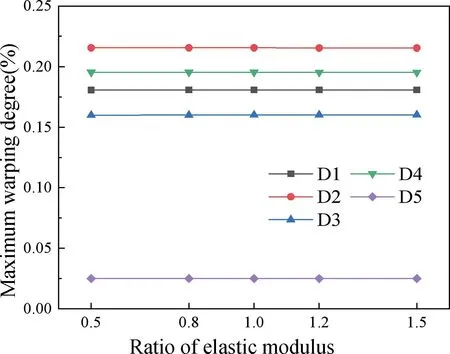
图9 不同焊球弹性模量下各芯片最大翘曲度Fig.9 Maximum warping degree of each chip with different elastic modulus of solder ball

4 结论

本文分析了以某PoP 模块在受热过程中产生的翘曲行为,探究了灌封胶膨胀系数、芯片厚度、焊球弹性模量对芯片翘曲的影响。仿真结果表明: 芯片受热时的主要翘曲形态为弓曲,上层封装内的芯片翘曲较大,在经历降温过程时,翘曲形态由上凸形转变为下凹形;相比于理想弹塑性本构模型,焊料的Anand 黏塑性本构模型能更准确预测芯片的热翘曲行为;芯片翘曲度随灌封胶热膨胀系数的减小而降低,随芯片厚度的增加而减小。