热循环加载下电子封装结构的疲劳寿命预测

刘江南 ,王俊勇 ,王玉斌

(1.西南交通大学 机械工程学院,四川 成都 610031;2.中车株洲电力机车研究所有限公司,湖南 株洲 412001)

美国空军某研究机构曾对电子设备的失效原因进行过概率统计,结果表明温度造成的失效是电子设备失效的最主要原因,其比例高达40%[1]。电子产品在服役期间,通常会经受电路的周期性通断以及温度急剧变化等情况,此时组件的温度载荷表现出周期性变化,这种周期性变化的温度载荷称为热循环载荷。封装结构在热循环的加载下,由于各组件材料间的热膨胀系数(CTE)不同,交变热应力不断作用于焊接部位,导致疲劳裂纹的萌生、扩展直至焊点断裂,致使电子设备失效[2]。

近十年来,美国、新加坡等发达国家通过创办专项基金大力支持微电子封装领域的可靠性研究,电子产品的可靠性成为研究热点。维持与提高产品的可靠性,成为国内外微电子行业中亟需解决的难题。林健等[3]使用试验分析方法,选用了两种不同的钎料以及两种不同尺寸的焊盘进行热循环试验。通过观察焊点截面上的裂纹萌生及扩展过程,研究了电子封装焊点结构在热疲劳过程中的疲劳裂纹扩展规律。宜紫薇[4]对某型号PCB 精细化建模,将63Sn37Pb 视为黏塑性材料,运用Coffin-Manson 高周疲劳经验公式预测随机振动载荷下的结构疲劳寿命;并基于Darveaux 模型预测PCB 在热循环加载下的热疲劳寿命;最后应用Miner 累积损伤理论,预测了模型在热循环与随机振动共同加载下的寿命。Wang 等[5]运用有限元与试验相结合的方法,提出了基于力学基础的疲劳试验原理,完成了等效加速热循环疲劳试验与数值模拟,并基于统一蠕变-黏塑性模型合理评估无铅钎料的本构参数。Le 等[6]探究了在温度循环加载下焊球空洞对焊点疲劳寿命的影响规律。通过运用MCRVE Gen 2D 算法随机生成焊点空洞,并基于有限元的原理,结合黏塑性能量方程对比分析了焊球内部空洞位置、分布及尺寸等参数对其可靠性的影响。

目前,对封装结构的热循环疲劳研究主要集中在BGA 封装形式上[7-12],而对QFP 与SOP 封装设备的数值分析方法研究相对较少。为探究某型号PCB 关键芯片在温度循环加载下的服役情况,本文对芯片的QFP 以及SOP 封装形式细化建模,并研究寿命最短焊点(危险焊点)的最大应力、应变分布规律,最后基于危险焊点的黏塑性应变能密度参数预测其疲劳寿命。

1 热疲劳分析理论基础

1.1 基于能量的Darveaux 模型

基于能量的Darveaux 模型[13]应用断裂力学理论,通过测量实际焊点的裂纹增长率,建立四个与裂纹增长相关的常数和两个控制方程。将有限元方法求解的结果带入方程计算初始裂纹产生时的温度循环次数和每个温度循环过程中裂纹的增长速率,进而预测焊点在完全失效时经历的温度循环次数。

使用Darveaux 模型预测焊点疲劳寿命分为三个步骤:预测裂纹萌生时的循环数;由裂纹增长速率预测裂纹扩展至断裂的循环数;预测焊点完全破坏时的循环数。

预测初始裂纹萌生时的循环次数N0的方程:

每个热循环中裂纹的增长速率dα/dN的方程:

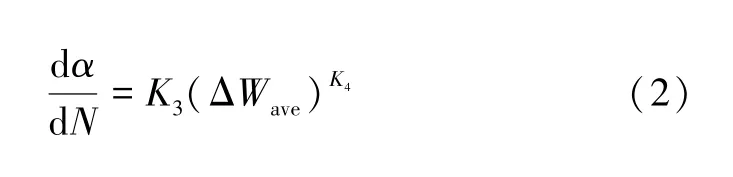
焊点疲劳破坏时的循环次数Nf的预测方程:

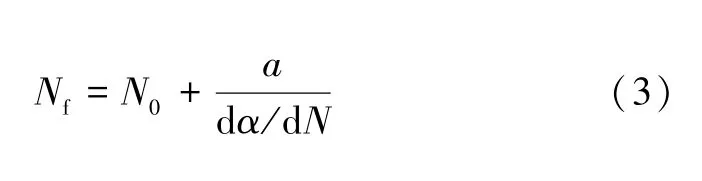
式中:K1、K2、K3、K4是随连接焊点和基板金属材料的厚度变化的常数;a是焊点直径;ΔWave是在每个循环焊点平均黏塑性应变能量密度的累积。

在焊点疲劳寿命的预测方程中,常数K1、K2、K3、K4可以通过查阅文献得到。本文使用的Darveaux裂纹扩展相关系数见表1。

表1 Darveaux 裂纹扩展相关系数Tab.1 Correlation coefficient of Darveaux crack propagation

1.2 Anand 黏塑性统一本构模型

20 世纪80 年代,Anand 等[14]探究了金属材料的单一内部变量与其非弹性变形间的规律,并提出了一种描述金属热变形的黏塑性统一本构模型,该模型就是目前在焊点热分析中广泛应用的Anand 模型。Anand 模型中的内部变量与晶粒尺寸、位错密度、固溶体强化效应等相关联,通过对宏观塑性流动的平均阻抗描述材料的各向同性强化。变形阻抗与等效应力成正比:

式中:c表示材料参数;s表示变形阻抗。材料参数c在应变速率恒定条件下可以近似看作常数:

式中:ζ表示应力因子;h表示应变硬化率;表示材料的非弹性应变速率;A表示指数因子;Q表示激活能;T表示热力学温度;R表示气体常量;m表示应变率敏感指数。

Anand 模型的黏塑性流动方程表示为:

内部变量的演化公式定义为:

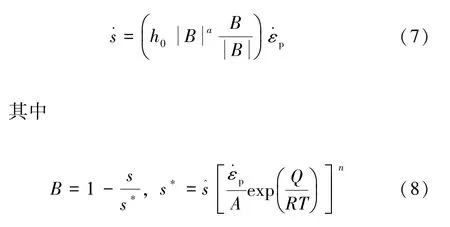
式中:h0表示强化系数,可以反映硬化/软化常数;a表示应变率敏感指数,其大小取决于硬化/软化特性;s*表示内部变量的饱和数值;、n表示材料的黏塑性相关系数。

2 有限元模型建立

PCB 的实物图如图1(a)所示。对PCB 的关键芯片焊点进行精细化建模,芯片的主要封装为QFP 和SOP 形式。QFP 与SOP 封装形式在外观上并不存在太大区别,参照文献[15]完成焊点建模。通过对PCB 的关键区域建立切片模型,可以实现模型的简化,建立的PCB 关键区域切片模型如图1(b)所示。

图1 PCB 关键区域切片三维模型Fig.1 Three-dimensional model of PCB critical area slices

2.1 材料属性

焊点使用非线性材料63Sn37Pb,具有随温度t变化的弹性模量。在热循环加载下,焊点不仅产生弹性应变与塑性应变,还产生与温度相关的蠕变变形,需采用Anand 黏塑性统一本构模型[14]来描述焊点的力学行为。Anand 本构模型的控制参数如表2 所示。表3为PCB 各组件的材料属性,其中导线、电路板与芯片均假设为各向同性线弹性材料。

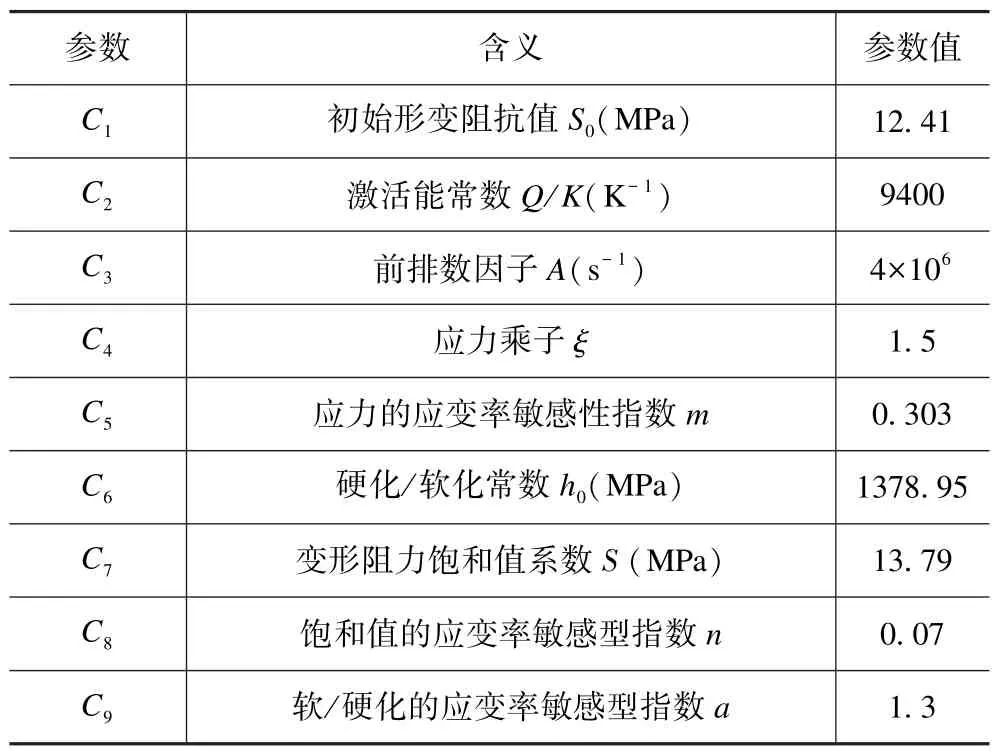
表2 焊料的Anand 本构模型Tab.2 Anand constitutive model of solder

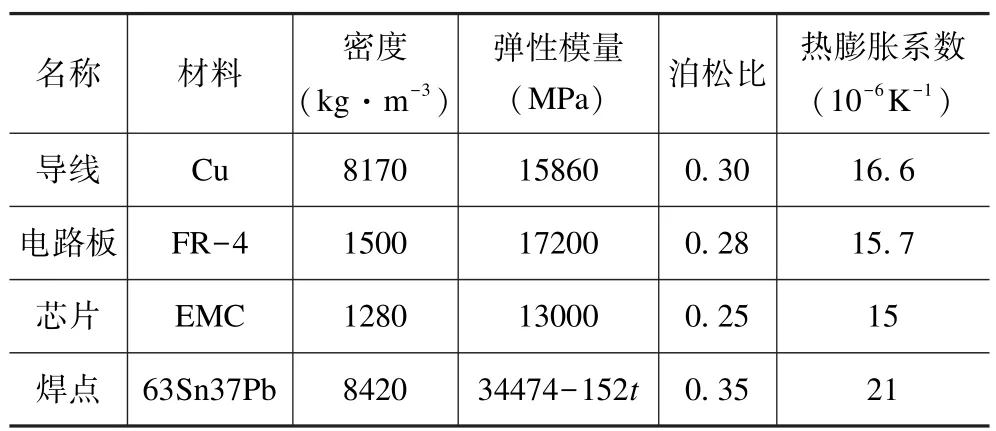
表3 PCB 各组件的材料属性Tab.3 Material properties of PCB components

2.2 网格划分

几何模型共有712 个部件,其中关键芯片7 块。使用六面体占优的网格划分技术与网格扫掠功能建立PCB 有限元模型,采用控制部件网格尺寸(Body Sizing)的方式调整网格质量,控制PCB 板的网格尺寸在0.8 mm 内,芯片的网格尺寸控制在0.7 mm 内,建立的有限元模型如图2。

图2 PCB 切片有限元模型Fig.2 Finite element model of PCB slicing

2.3 温度载荷的加载

热循环温度加载,参考国军标GJB 150.5A-2009温度循环试验加载标准,最高加载温度为125 ℃,最低加载温度为-55 ℃,整个温度循环过程温差达到180℃,零应力下的参考温度为20 ℃。

PCB 的温度循环加载曲线如图3 所示,对PCB 施加4 个温度循环载荷,单个温度循环经历: 高温保温阶段,历时15 min;降温至低温阶段,历时15 min;低温保温阶段,历时15 min;升温至高温阶段,历时15 min。每个温度循环分为4 个载荷步,每个载荷步设置为6 个子步,以提高迭代精度。

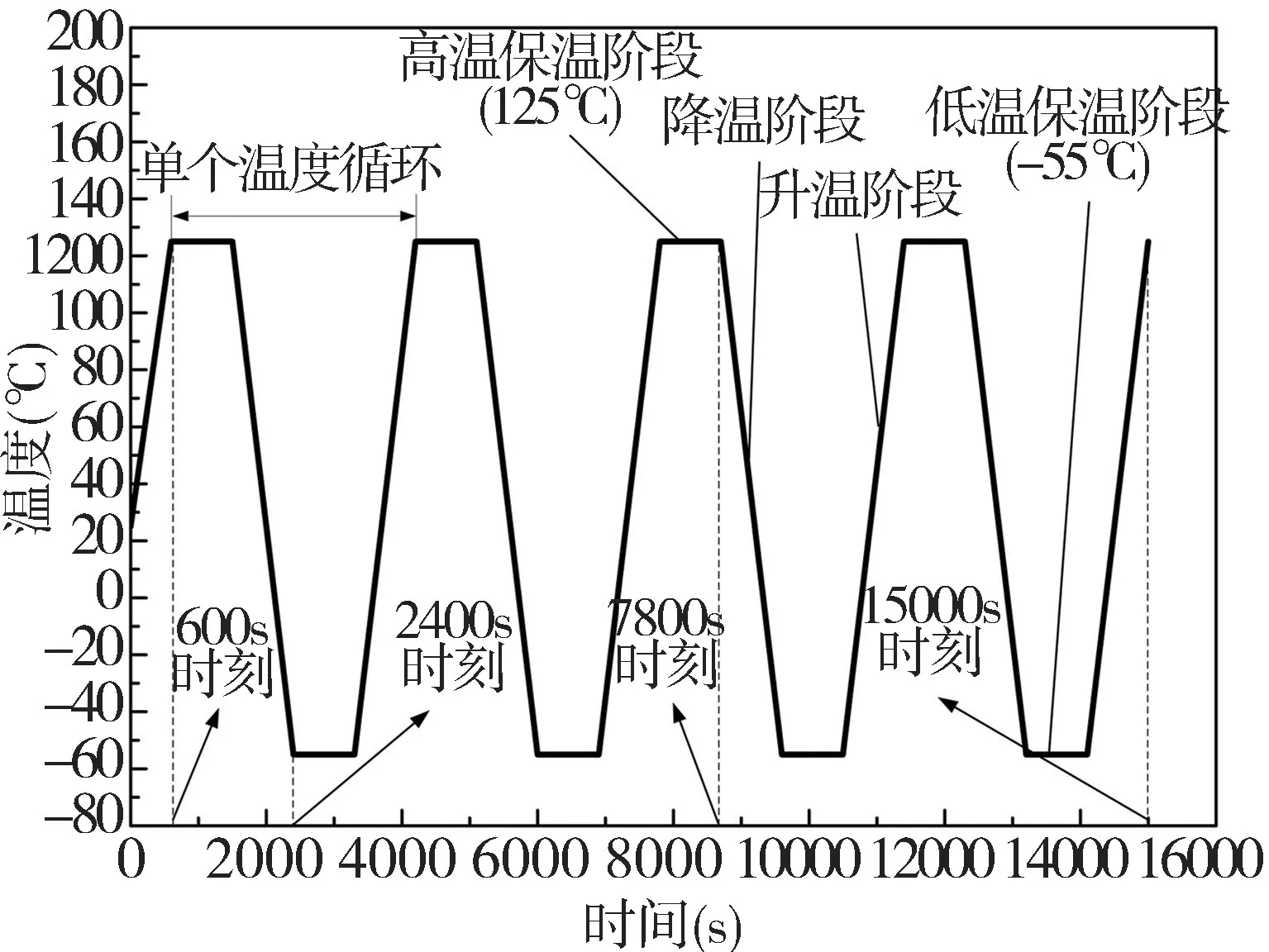
图3 温度循环加载曲线Fig.3 Temperature cyclic loading curve

3 电子封装热循环仿真分析

通过非线性应变能密度参数判断模型的危险焊点位置,结合危险焊点的等效应力、应变规律绘制迟滞曲线。基于迟滞曲线得到稳定的温循次数,最后使用Darveaux 模型判断典型封装结构的热疲劳寿命。

考虑到焊点在温度周期变化下的疲劳失效是一个瞬态过程,因此选用ANSYS Workbench 软件中的Transient Structure 模块进行热疲劳分析。

3.1 焊点的黏塑性应变能密度分析

黏塑性应变能密度的大小决定焊点的寿命。根据焊点黏塑性应变能密度云图中最大值的出现区域,可判断典型芯片封装结构中寿命最短焊点,即危险焊点的位置。

图4 表示危险焊点的黏塑性应变能密度分布,其中图4(a)为切片模型整体的黏塑性应变能密度云图,将黏塑性应变能密度最大的焊点视作危险焊点;图4(b)为危险焊点的黏塑性应变能密度云图,焊点的应变能密度由上至下出现明显的分层现象,焊点下部的黏塑性应变能密度明显高于上部区域。切片模型的最大黏塑性应变能密度出现在QFP 封装芯片的下部最左端焊点,为焊点与电路板接合面焊趾处。

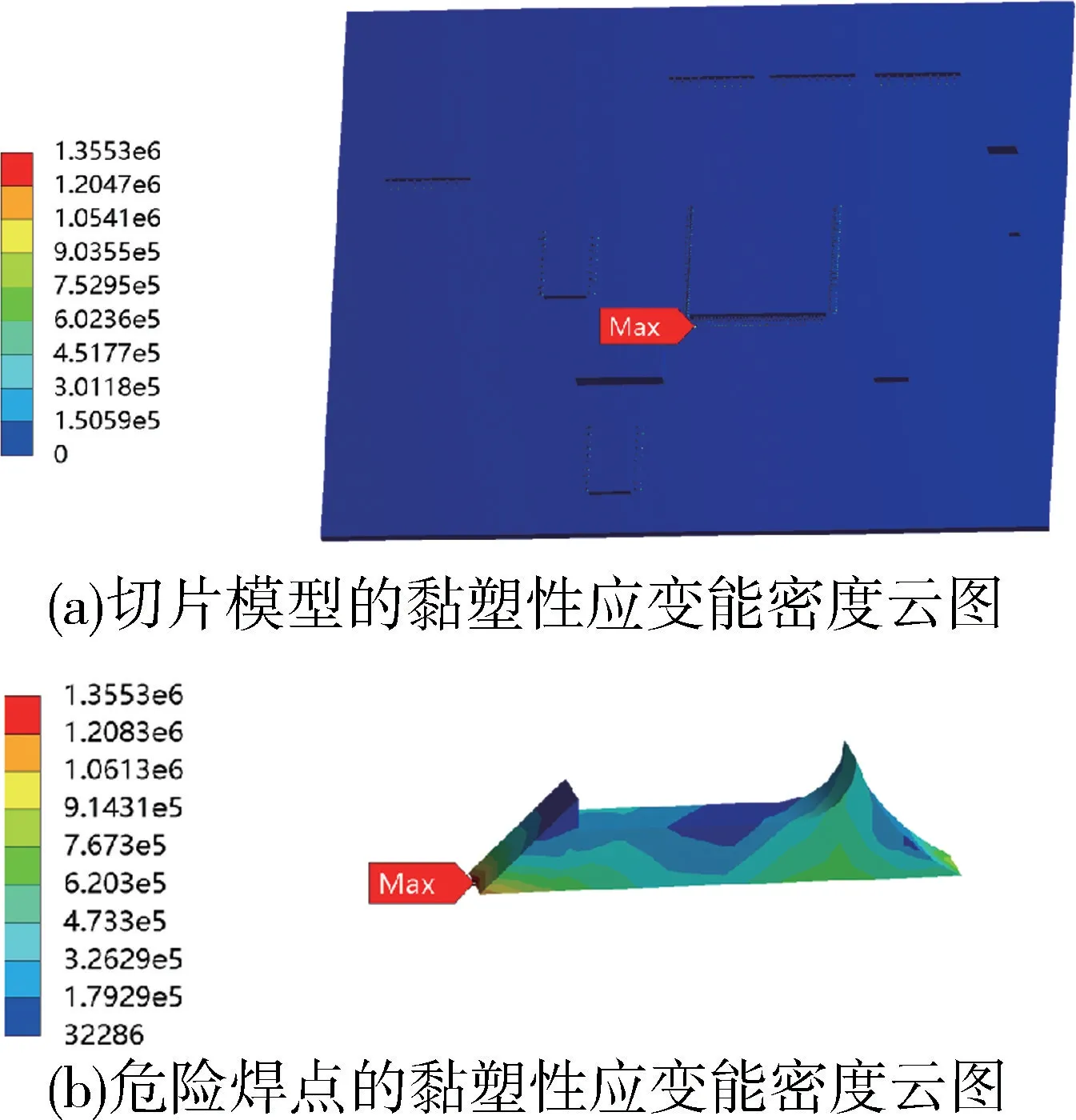
图4 危险焊点的黏塑性应变能密度云图Fig.4 Viscoplastic strain energy density cloud of dangerous solder joints

图5 表示温度循环过程中危险焊点的最大黏塑性应变能变化规律,随着时间的推移,焊点的黏塑性应变能密度呈逐渐上升趋势。表明焊点存在黏塑性的应变能累积特性,验证了锡钎焊点的Anand 黏塑性特征。

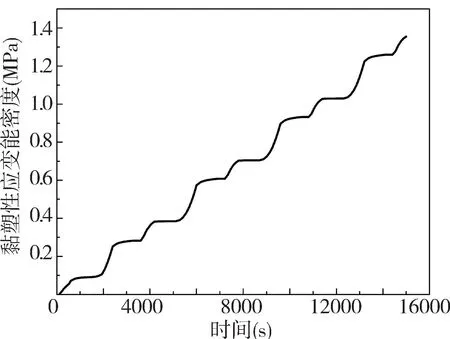
图5 危险焊点最大黏塑性应变能密度变化规律Fig.5 Variation law of maximum viscoplastic strain energy density of dangerous solder joints

3.2 焊点的等效应力分析

为探究危险焊点在温度循环不同时刻的应力分布,分别选取温度循环中600,2400,8700,15000 s 四个典型时刻。这些时刻囊括了高温(125 ℃)和低温(-55℃)时刻,可以研究焊点在经历温度循环前后以及不同温循中温度相同时刻等效应力分布情况。图6 为危险焊点在4 个典型时刻的瞬态应力分布云图。

图6 危险焊点的瞬态应力分布Fig.6 Transient stress distribution of dangerous solder joints

分析可知,焊点的等效应力分布呈两端大中间小的规律,4 个典型时刻的等效应力最大值并未出现在同一区域。2400 s 时刻危险焊点承受应力水平最高,最大应力约为56.1 MPa,应力集中位置与黏塑性应变能密度的最大值区域相同。8700 s 时刻危险焊点承受的应力水平最低,最大应力约为1.49 MPa。

因为焊点与电路板在垂直方向上的热膨胀系数失配以及温度循环过程中引线对焊点的拉伸作用,致使焊点的局部区域产生应力集中。分析结果与张亮等[16]数值计算结果相吻合,由此可判断疲劳裂纹最初将在危险焊点与电路板接合面焊趾处产生。

图7 为危险焊点中危险区域的等效应力-时间关系曲线,在四个温度循环内危险焊点中危险区域的等效应力分布规律较为相似,且数值呈现周期性变化。危险焊点的最大等效应力约为61.6 MPa,最小等效应力约为1.49 MPa。危险焊点中危险区域的等效应力在降温结束时达到较高水平,在低温保温阶段呈略微下降趋势;在升温结束时到达低点,并在高温保温阶段持续降至最低。

图7 危险焊点中危险区域的等效应力-时间关系曲线Fig.7 Equivalent stress-time curve of dangerous zone of dangerous solder joints

3.3 焊点的等效塑性应变分析

为研究危险焊点等效应力与等效塑性应变间的关系,选取相同时刻仿真。图8 表示典型时刻危险焊点的瞬态应变分布,危险焊点的最大塑性应变位置均为焊点与铜引线接触的直角边缘处。

图8 危险焊点的瞬态应变分布Fig.8 Transient strain distribution of dangerous solder joints

四个典型时刻中,危险焊点的等效塑性应变呈左端大右端小的分布规律,600 s 时刻危险焊点中危险区域的塑性应变最低,应变统计值约为0.0106;15000 s时刻的塑性应变最高,应变统计值约为0.0193。

图9 为危险焊点中危险区域的等效塑性应变-时间关系曲线,危险焊点的最大塑性应变随着温循的加载呈累积上升趋势。最初由室温升高至125 ℃时,应变的统计值增量最大,约为0.0106;在剩余的四个温度循环内,焊点的塑性应变持续升高,每个温度循环均对应着焊点塑性应变的累积,当经历第四次温度循环后,危险焊点的等效塑性应变到达峰值。

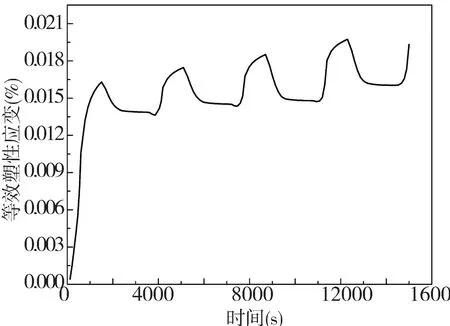
图9 危险焊点中危险区域的等效塑性应变-时间关系曲线Fig.9 Equivalent plastic strain-time curve of dangerous zone of dangerous solder joints

3.4 焊点的应力应变规律分析

根据不同时刻危险焊点的应力-应变变化情况,可绘制出应力-应变迟滞环。应力-应变迟滞环的产生是由于黏塑性焊点的塑性变形累积和应力松弛作用,导致焊点的等效应力与等效塑性应变两者最大值不在同一时刻出现。应力-应变迟滞环的环形面积表示每一个周期热循环加载下结构积累的塑性功,面积相同即达到稳定状态。图10 为绘制的危险焊点应力-应变迟滞环,迟滞环呈周期性的变化趋势,且四个迟滞环正好对应着四个温度循环周期。最后两个迟滞环面积相同且形状一致,因此可判断PCB 的热循环在进行到第三次温度循环时到达稳定状态,焊点的黏塑性应变能量密度在此后趋于稳定,仿真成功。

图10 危险焊点的应力-应变迟滞环Fig.10 Equivalent stress-strain hysteresis ring of dangerous solder joints

3.5 危险焊点的热疲劳寿命预测

由于ANSY Workbench 无法直接输出焊点的平均黏塑性应变能量密度ΔWave,本文采用ACT 插件Solder Joint Fatigue 进行焊点的疲劳寿命预测。

基于Darveaux 热疲劳模型,参考公式(1)～(3),计算危险焊点的热疲劳寿命。结果显示: 初始裂纹萌生时的循环次数N0为7 个周期;每个热循环中裂纹的增长速率dα/dN为1.037×10-4mm/cycle;焊点的断裂特征长度a=0.529 mm,完全疲劳破坏时的循环次数Nf为209 个周期。

4 结论

在热循环加载条件下,由于焊点垂直方向上的热膨胀系数失配,以及引线对焊点的拉伸作用,将导致封装焊点出现局部的应力集中。本文研究分析表明危险焊点的应力集中区域为焊点与电路板接合面焊趾处。危险焊点中危险区域的应力呈周期性分布,低温时的应力水平远高于高温时刻;等效塑性应变随温循的加载呈累积上升趋势。分析结果与文献[16]数值计算结果基本吻合。最后基于Darveaux 热疲劳模型,预测危险焊点初始裂纹萌生时的循环次数为7 个周期,疲劳破坏时的循环次数为209 个周期。在PCB 的设计与实际运用阶段,需重点关注芯片焊点结构的应力应变及失效情况,进而提高整板的环境适应性、减少潜在的缺陷。