高真空密封环境下超高速实心转子电动机温度特性分析
2022-10-21赵岩庆王子羲郭辉孙凤姚佳康
赵岩庆,王子羲,郭辉,孙凤,姚佳康
(1.沈阳工业大学 机械工程学院,沈阳 110870;2.清华大学 摩擦学国家重点实验室,北京 100083)
能源动力设备是国民经济的基础和命脉,高转速、高功率密度、耐高温等是当前能源动力设备的主要发展方向。电动机是能源动力设备的关键核心器件,其高转速和耐高温性能已成为国内外专家学者关注的研究内容[1]。文献[2]研制了一台0.6 kW,2×105r/min的高速永磁无刷直流电动机,并对其进行了理论分析;文献[3]设计了一台0.6 kW,2×104r/min的高速永磁电动机,并对电动机损耗问题进行分析;文献[4]研究了静压气浮直驱转台结构的热稳定性;文献[5]通过给定气体内外径出口边界为压力边界,止推盘为旋转壁面,对止推轴承温度场进行了仿真与试验研究,提出可以通过调节进气压力使轴承温度得到合理控制;文献[6]对箔片气体轴承温度特性进行试验,验证了稳定状态下的轴承温度会稳定在某一值。
随着电动机转速显著提高,风磨损耗已成为不可忽视的关键因素,在高真空密封环境下对高速电动机进行研究可有效解决高速电动机风磨损耗大的问题,但是目前对电动机在高真空密封环境下的研究相对较少[7],没有形成系统的研究方法。同时,高速时转子所受的机械应力较大,因此转子一般采取实心结构[8]。
目前,高速电动机支承技术以高速精密滚动轴承为主,其技术成熟,支承系统结构简单,但是受到物理摩擦的影响,轴承损耗及发热问题限制了电动机的高速性能。为有效提升支承技术的高速性能,需要依赖现有技术的突破和新技术的应用,目前正在快速发展的气浮轴承技术[9-12]可以帮助解决上述问题。气浮轴承工作时,固定的轴承座表面与旋转的转子表面之间产生楔形间隙,高速转动的转子将气体带到楔形间隙中形成动压气膜,具有一定压力的动压气膜将转子撑起,使转子能够正常承载运行,该工作方式可以明显降低轴承损耗,提高电动机运行效率。随着高速旋转机械对转速和可靠性的要求不断提高以及工作环境的日益恶劣,气浮轴承支承凭借其耐高温、低摩擦、自适应稳定等特征,成为高速电动机的重要发展趋势之一[13]。
综上,为解决高速电动机风磨损耗大,高速时转子所受机械应力大,滚动轴承发热严重等问题,本文提出了一种在高真空度工况下以气浮轴承为关键支承技术的超高速实心转子电动机结构。为实现高真空工况下实心转子超高速电动机的长时间可靠运行,研究了其损耗及传热特性的理论方法,进而实现温度场的准确、快速计算;通过有限元分析了电动机主要部分温度分布规律,以提高对超高速电动机温度特性的认知。
1 高速电动机的损耗
损耗越大,电动机的温升幅度越大,尤其是在高真空环境下温升幅度会更大,从而影响电动机的正常运行。电动机在真空状态下工作时,产生的损耗主要有铜损耗、涡流损耗、铁损耗、风磨损耗和轴承损耗,占比较大的为绕组铜损耗和定子叠片损耗,由于转子铁心损耗很小,且计算较复杂,在计算时可以忽略[14]。
本文提出一种在高真空度工况下以气浮轴承为关键支承技术的超高速实心转子电动机,其结构示意图如图1所示。由于密封结构位于真空腔外侧,有很好的冷却条件,所以关于温度场的研究忽略密封结构的影响。
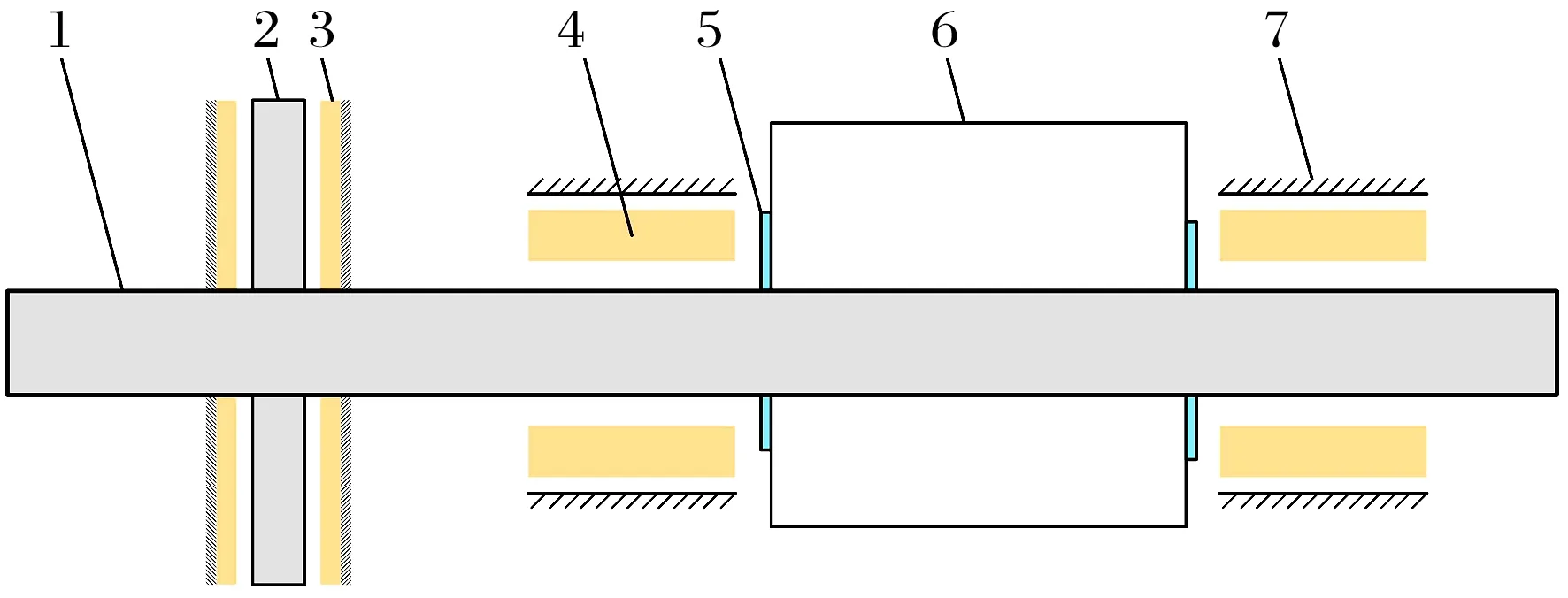
1—转子;2—止推轴承;3—推力盘;4—箔片动压径向轴承;5—密封结构;6—真空腔;7—轴承座。
1.1 风磨损耗
与普通电动机相比,高速实心转子电动机的转子表面速度较高,风磨损耗较大。风磨损耗可分为轴向通风和转子旋转引起的损耗[15]。高真空环境下不存在轴向通风引起的损耗,因此只需计算由转子旋转引起的损耗。
实心转子表面的风磨损耗取决于转子的转速、表面粗糙度以及空气的性质,即
Pw=KCfπρar4ω3l,
(1)
式中:Pw为转子风磨损耗;K为转子表面粗糙度;Cf为圆柱拖拽系数;ρa为空气密度;r为转子半径;ω为转子角速度;l为转子长度。
圆柱拖拽系数与转子附近空气的雷诺数有关,而转子上的雷诺数为径向雷诺数,是由转子旋转引起的空气摩擦,即
(2)
式中:δ为转子与电动机的气隙宽度;μ为气体动力黏度,只与气体温度有关。
1.2 实心转子表面涡流损耗
电枢反应磁场是实心转子表面涡流损耗产生的主要原因。在高速实心转子电动机中,根据转子铁磁材料的磁化曲线与相对磁导率曲线可以计算出金属内高频涡流屈服深度,即
(3)
式中:f为谐波频率,Hz;γ为电导率,S/m;μM为磁导率,H/m,是相对磁导率与真空磁导率(4π×10-7H/m)的乘积。
根据表面涡流损耗分析,高频涡流损耗为
(4)
式中:Bm为交变磁场幅值;V为存在涡流损耗的体积;k为形状系数,对于金属壳取1,对于电线取2。
金属壳平面涡流损耗密度为
(5)
式中:S为金属壳平面的表面积。对于无明显趋肤效应的结构(如硅钢片),pp/S∝f2。
电线导线内涡流损耗密度为
(6)
式中:dc为导线直径;Nc为线圈匝数与并绕根数的乘积。对于无明显趋肤效应的导体(如利兹线、细漆包线),pw/S∝f2。
1.3 高频定子铁耗
利用硅钢片在工频正弦波电源励磁下的损耗特性及相关的经验公式,可以得到高频定子铁耗为
PFe=Ph+Pc+Pe=
(7)
式中:PFe为铁耗;Ph为磁滞损耗;Pc为经典涡流损耗;Pe为附加涡流损耗;kh,x为磁滞损耗系数;fF为基波频率;Bp为磁通密度幅值;kc为经典涡流损耗系数;ke为附加涡流损耗系数。
1.4 高频电枢铜耗
与传统电动机相比,高速电动机因其高频特性使绕组上产生了显著的集肤效应及邻近效应,产生的铜耗较多,导致电动机温度升高,效率降低。因此在分析计算绕组铜耗时应考虑集肤效应及邻近效应,从而更准确计算高速电动机的绕组铜耗。
高速实心转子电动机电枢绕组铜耗可表示为
Pac=Pad+Pdc=nI2R+nI2R(kd-1),
(8)
式中:Pac为电枢铜耗;Pad为附加涡流损耗;Pdc为直流损耗;n为电动机相数;I为电流有效值;R为直流电阻;kd为平均电阻系数。
由文献[16]可知平均电阻系数与频率的关系为:1)f<12 kHz时,kd<1.01;2)f=50 kHz时,kd=1.16。
电动机的目标转速为1.0×105r/min,频率为5 kHz,为减小其铜耗,故采用利兹线,因此在分析时可忽略集肤效应对绕组电阻的影响,由直流电阻阻值近似等效交流电阻阻值,则绕组电阻为
(9)
式中:ρ为100 ℃时铜的电阻率;LZ为绕组线圈半匝的长度;ZΦ1为每相匝数;a1为相绕组的并联数;S1为导线截面面积;N1为线圈并绕根数。
1.5 气浮轴承损耗
箔片动压轴承的损耗主要由启动或停车过程中轴承与转子表面发生接触产生,箔片动压轴承完成一次启停,总的损耗为
W=Wu+Wd,
(10)
(11)
式中:Wu为速度上升时的损耗;Wd为速度下降时的损耗;aω为转速影响因子,aω<0;bω为转子与箔片间摩擦因数;aT为温度影响因子,aT<0;T为环境温度;bT为材料摩擦因数。
在轴承启动阶段,旋转速度与时间成线性关系,即ω=kω1t,代入(11)式得
(12)
A=k(aTT+bT),
式中:t1为轴承起飞时间。
在轴承停车阶段,旋转速度也是时间的近似线性函数,即ω=kω2(t-Δt)+tω1t1,Δt为轴承停车开始时刻,轴承速度下降时的损耗为[17]
(13)
式中:t2是停车所用时间。
箔片动压轴承完成一次启停总的磨损量为
Abω(t1+t2)。
(14)
根据上述分析可得,kω1=ωz/t1,kω2=ωz/t2,代入(14)式得
(15)
式中:ωz为转子起飞速度。
2 高真空密封环境热辐射计算方法
在高真空环境下,电动机仅能依赖辐射散热,而热辐射传递无需介质,可以在空气与真空中进行,特别是在真空中效果最好[18]。不同物体间辐射散热公式为
Q=εσAFijΔT4,
(16)
式中:ε为物体表面的辐射率;σ为斯忒藩-玻尔兹曼常数;A为辐射面的散热面积;Fij为辐射物体的角系数;ΔT为两辐射面的表面温度值,K。
由(16)式可知,不同物体之间的散热量与材料辐射率、辐射面的温度和角系数等参数有关,其中角系数的计算公式为
(17)
式中:Ai,Aj为2个辐射面的散热面积;r为2个辐射面之间的距离;θi,θj分别为辐射散热面法向与散热面i,j之间的夹角。辐射角与散热面之间的关系如图2所示。
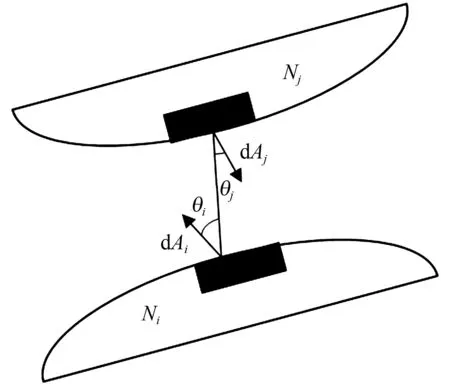
图2 辐射角与散热面的关系
综上,热辐射的角系数仅与散热物表面有关,当物体的表面形状一定时,角系数为定值。
考虑电动机无环境辐射的苛刻条件,仅对电动机内部辐射进行考虑。电动机内各表面热辐射设置如图3所示。
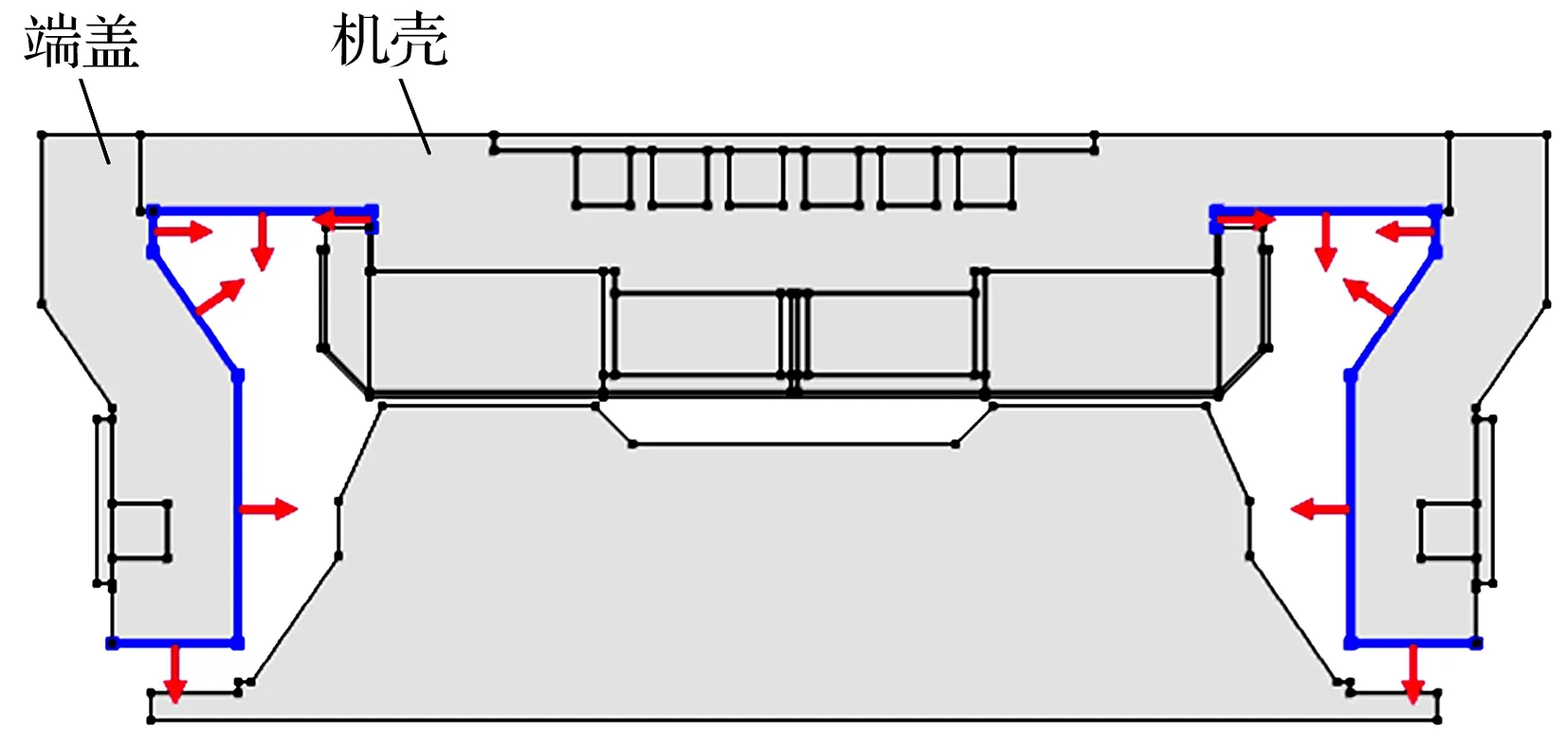
(a)机壳及端盖表面
根据辐射散热公式可知,电动机在高真空环境中的辐射散热与散热表面面积呈非线性关系,辐射热量取决于辐射表面发射率,提高散热表面的辐射率可以有效降低电动机的温升。
3 温度场分析
前文对高速实心转子电动机的热源以及可能存在的损耗进行了计算分析,在此基础上,利用COMSOL有限元分析软件,将各部件的损耗和相关系数引入电动机模型中,以研究电动机内部传热情况,分析各部件的温度变化规律。
3.1 箔片动压止推轴承传热分析
轴承在高速运行时,内部热量传递模型如图4所示。整个转子系统可以沿着轴向方向划分为6个区域来描述传热情况。气膜内部产生的热量首先通过止推盘(区域B)向周围环境传递(区域A),或向顶箔侧传递(区域C),然后通过热传导或热对流(区域D)传递到轴承座(区域E),最终传向大气环境(区域F)[19]。
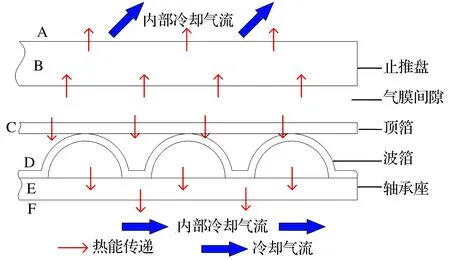
图4 箔片动压止推轴承热量传递模型
当箔片内通入冷却气体时,气膜内产生的热量一部分经顶箔传递,其中80%被冷空气带走[20],剩余部分则传递给波箔,进而传递到轴承座,通过热对流传到周围环境。同时,热流也将通过波箔表面和轴承座内表面传输到空气中。
气膜内部产生的热量的另一部分传向转子,经辐射散热传出。这个过程满足能量传递的连续性,其中从气膜到转子的热流Q1为
(18)
轴承向转子传递的热流Q2为
(19)
式中:ξ为气膜导热系数;h为气膜厚度;L为轴承宽度。
3.2 电动机转速与励磁调节曲线
为了更加准确地反映电动机温升动态变化,需要配合实际的电动机调速曲线对电动机损耗变化进行设置。本文考虑电动机调速全程采用理想正弦波方法,高速弱磁则通过降低励磁电流实现,由于高速实心转子电动机电枢反应磁场远小于励磁磁场,因此可认为电动机气隙磁场和端电压大小主要由励磁磁场限制。采用励磁电流弱磁控制方式,可以得到相应的电动机调速曲线如图5所示。
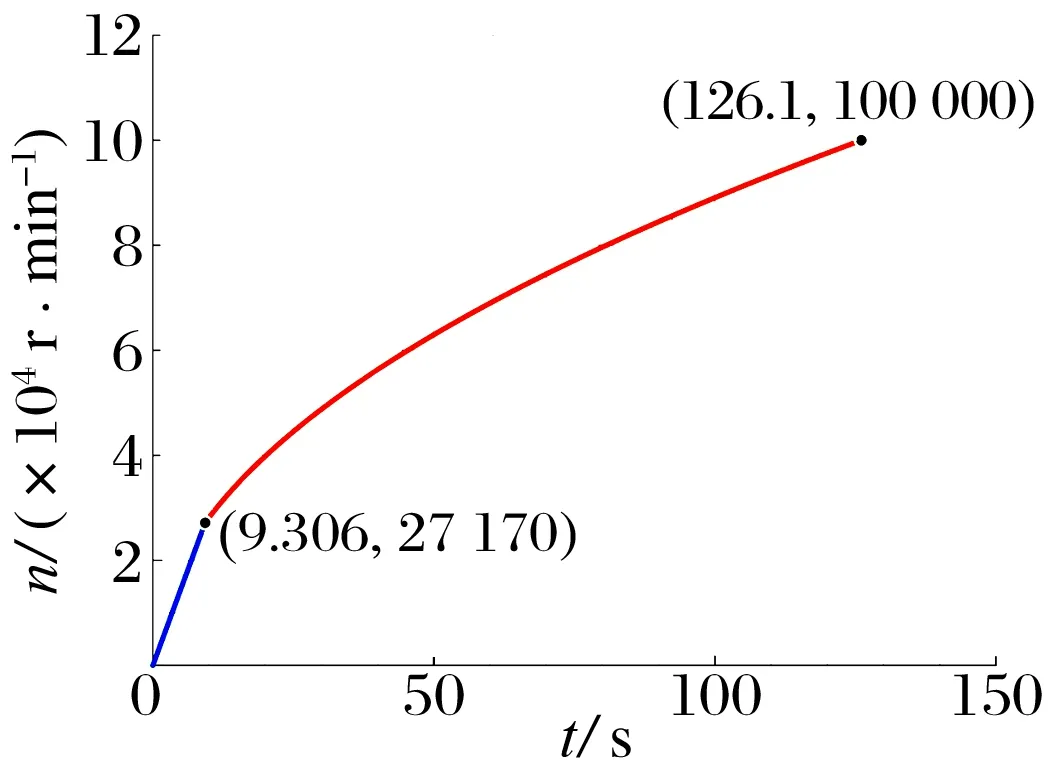
(a)升速曲线 (b)转矩曲线 (c)励磁控制曲线
将上述曲线标注值函数表示为时间的函数输入到仿真模型中,仿真模型可表示为
(20)
(21)
式中:fM为电动机频率;η为电动机效率,取η=0.95;TN为电动机额定转矩;tm为电动机的升速时间;J为转动惯量;ΩN为电动机极对数与额定角速度的比值,ΩN=p/ωN;Ωm为电动机极对数与最大角速度的比值;PN为电动机额定功率;tN为额定转折时间;If为励磁电流;1.5为安全时间系数;n为转速;nN为电动机额定转速。
根据上述仿真模型可以得到相应的频率和励磁电流标注值曲线,如图6所示。
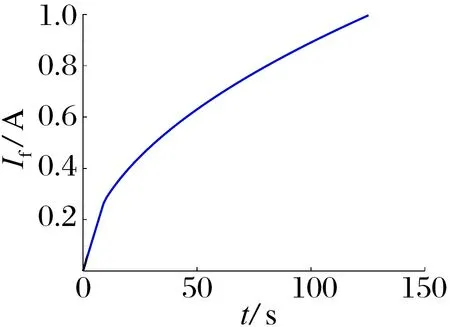
(a)励磁函数 (b)转矩函数
3.3 温度场仿真
在气体轴承中热量的传递主要有热传导和热对流2种方式。因热传导相对于热对流产生的热量小,可以忽略,为简化仿真模型,减小计算量,将气膜与转子及箔片间的传热量集中到一个单一的变量参数,对转子系统添加一个热源[21]。根据上文电动机转速与励磁调节曲线的仿真模型,可以得到对应的动态变化函数,如图7所示。计算得到最终时间点的电动机温度云图如图8所示。
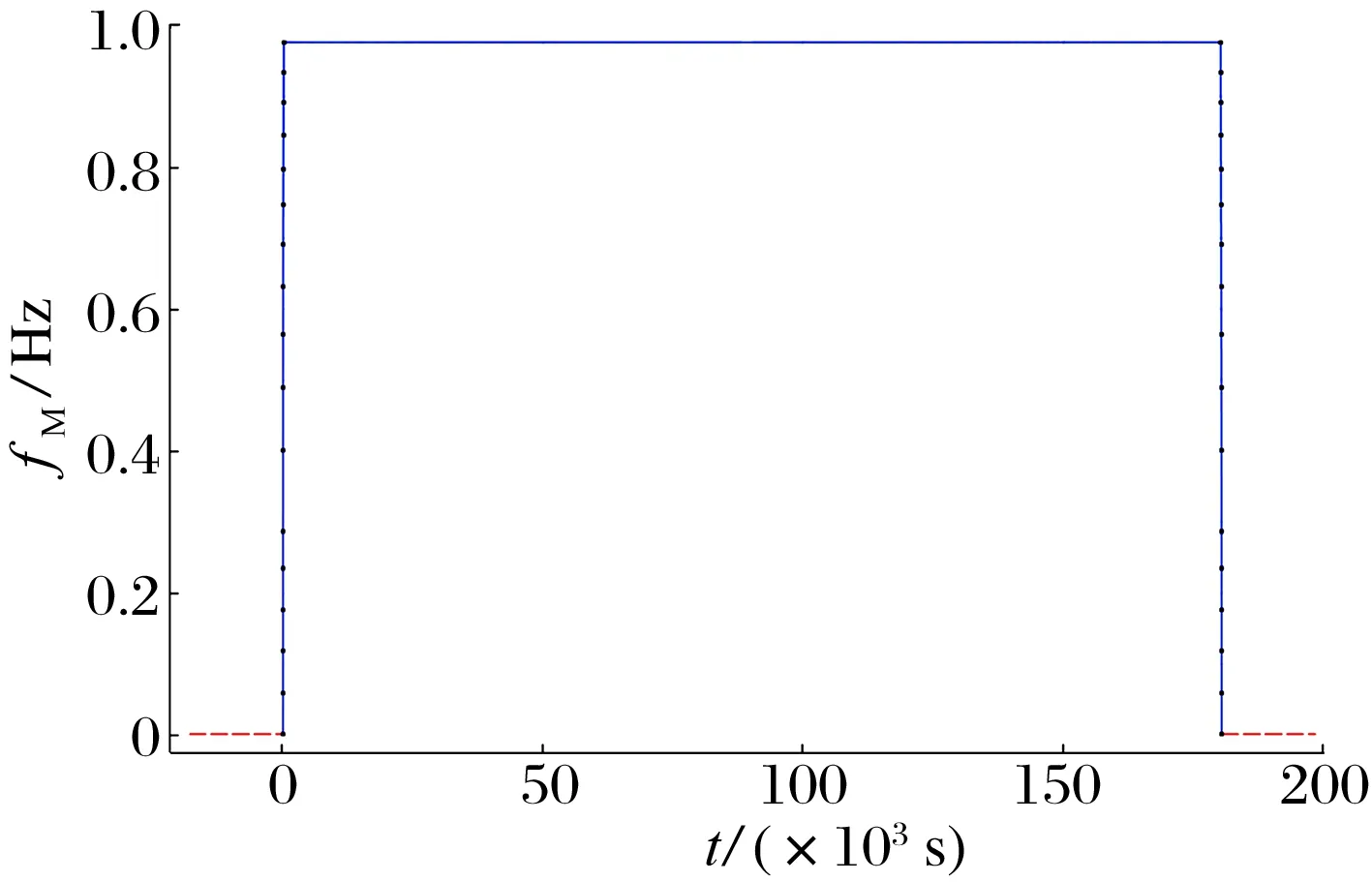
(a)转速/频率函数
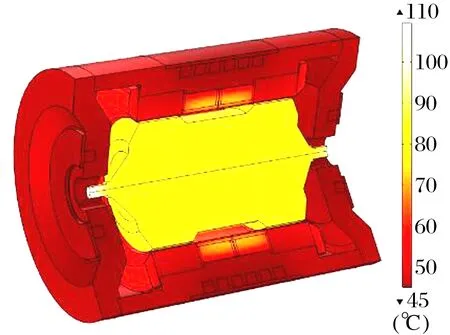
图8 电动机温度云图
除转子系统外,可以看到电动机温升最大位置在电枢和励磁绕组处,提取这2个位置的最大温度曲线如图9所示:励磁最高温度为70 ℃,电枢最高温度为63 ℃。
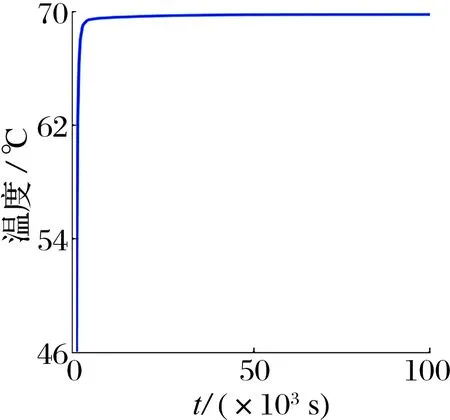
(a)励磁绕组 (b)电枢绕组
根据上述仿真结果,可估测励磁最大温升不超过65 ℃,则该电动机结构具备短时和长期运行能力。
4 结束语
针对高速电动机风磨损耗大,高速时转子所受机械应力大,滚动轴承发热严重等问题,提出了高真空密封环境高速实心转子温度计算方法, 通过温度计算分析,电动机转速在1.0×105r/min时,电枢绕组、励磁绕组、转子的最高温度在允许范围内,初步验证了高真空环境下气浮轴承支承的超高速实心转子电动机结构的可行性。
