基于轨迹法的气体箔片轴承动态特性系数辨识

程文杰，柯涵章，肖玲，李明

(西安科技大学 理学院，西安 710054)

气体箔片轴承(Gas Foil Bearing，GFB)利用环境气体作为润滑介质，通过动压效应在轴承表面产生气膜压力使转子悬浮，具有污染小，精度高，噪声低，工作温度范围广，耐冲击等优点，在透平机械、高速电动机、涡轮压缩机等领域应用效果良好[1-4]。

当GFB受到外部因素影响时，转子会随载荷的变化在轴心附近振动，轴承的动态特性系数(动态刚度系数和动态阻尼系数)能反应转子受外载荷作用下气膜力与位移和速度之间的内在联系[5]，有必要探讨GFB的动态特性系数计算方法[5]。

国内外学者对GFB的动态特性系数计算做了一定研究：文献[6]基于摄动法的思想，用动态刚度系数、动态阻尼系数表征GFB 在静态工作点邻域内的支承力；文献[7]采用偏导数法计算了GFB的动态特性系数，结果表明动态特性系数仅与转子扰动频率、轴承静载荷及轴承数有关；文献[8]建立了GFB的完全气弹润滑耦合解模型，得到了GFB的动态特性系数，结果表明动态特性系数仅与轴承结构参数、静态工作点参数以及扰动频率有关；文献[9-10]将箔片变形和润滑气膜的雷诺方程耦合求解，基于摄动法求解GFB的动态特性系数，并采用牛顿-拉弗森迭代法求解，得到了不同偏心率、转速、扰动频率及轴承长径比等参数下的动态特性系数；文献[11]将箔片等效为弹簧阻尼系统，考虑弹性波纹结构内部的库仑摩擦效应和相邻拱之间的相互作用，基于摄动法计算了GFB的线性化刚度和阻尼；文献[12]搭建了GFB的动态特性测试试验台，通过在频域内求解运动方程分析了激振频率和转子转速对轴承动态特性系数的影响，结果表明轴承主刚度随激振频率增大而增大，主阻尼随激振频率增大而减小。

上述研究均为基于摄动法计算GFB的线性化刚度和阻尼，即计算给定涡动比下的动态刚度系数和动态阻尼系数，实际工况下GFB的涡动比未知，摄动法仅考虑单个涡动比，而轴承可能存在多个涡动比。此外，限于摄动法的思想，力系数法对处理转子大范围运动的问题非常繁琐。

针对摄动法存在的问题，许多学者采用参数辨识方法得到GFB的动态特性系数：文献[13]通过测量转子的质量、力和动力学响应获得了系统的动态刚度系数和动态阻尼系数，但忽略了外部扰动对系统的影响；文献[14]通过动态载荷法，将不平衡质量作为系统的激振力，获得了以激振频率和转子转速为函数的动态特性系数，但计算较为繁琐；文献[15]采用未知激励力的方法研究了多自由度系统的动态特性系数辨识问题，并通过数值仿真验证了方法的正确性，但计算的动态特性系数是线性的；文献[16]通过Volterra法和谐响应探头法辨识轴承的动态特性系数，但只考虑了响应的线性部分而忽略了非线性因素；文献[17]通过锤击激振法和摄动法计算轴承的动态特性系数，2种方法结果接近，但锤击激振法计算过程中假设主刚度相等，交叉阻尼互为相反数；文献[18]通过改变长径比、偏心率、轴承数、涡动比等参数，采用摄动法计算GFB的动态特性系数，并利用得到的数据训练了一个神经网络模型，基于神经网络有效地辨识出GFB的动态特性系数，但训练神经网络的数据仍是基于摄动法。

参数辨识方法已经有了一定的发展，但均存在一定的缺点。鉴于此，基于时域轨迹法建立气体箔片轴承-转子系统的流固耦合动力学模型，并求解简谐激励载荷下转子的瞬态轨迹，最后采用线性简谐激振法和简谐激振法辨识出轴承的动态特性系数。

1 基于时域轨迹法的GFB-转子系统动力学模型及求解

1.1 GFB的基本方程

任意扰动下气体轴承与转子的位置关系如图1所示，等温动压气体润滑雷诺方程的量纲一化形式为

(1)

Λ=6μω(R/C0)2/pa，

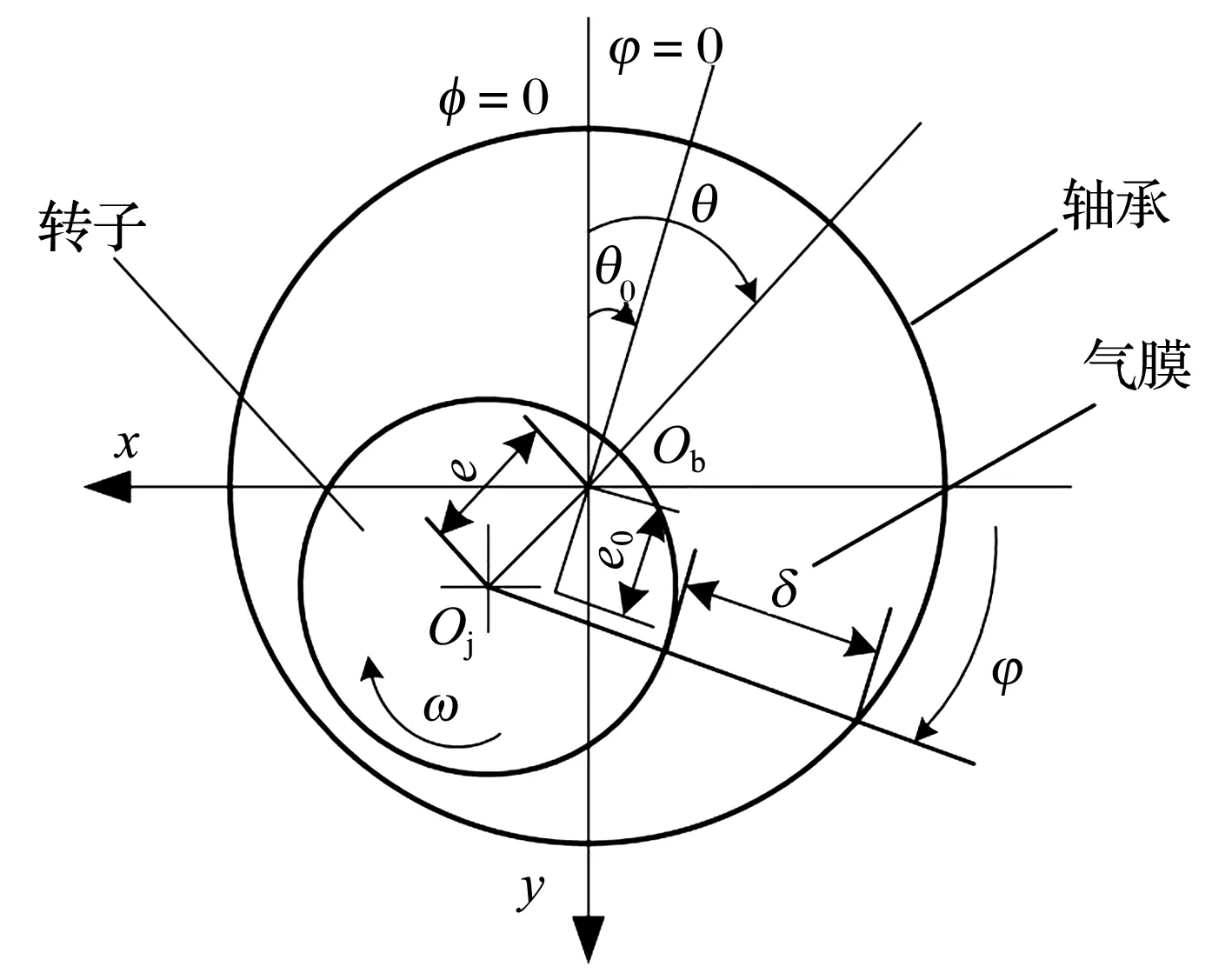
图1 任意扰动下气体轴承与转子的位置关系示意图

若仅考虑转子在轴承静态偏心处的定轴转动，由于轴承半径间隙C0远小于转子半径R，忽略高阶小量后的气膜厚度为

h=C0+ecos(φ-θ)，

(2)

式中：e为转子偏心距；φ为轴承展开角；θ为转子静态偏位角。

1.2 瞬态气膜压力分布的数值求解

(3)

σ=2Λ。

采用交替隐式迭代法求解(3)式，空间变量的离散采用中心差分格式，时间变量的离散采用向后差分格式，把一个时间步长分为n～n+1/2和n+1/2～n+1。具体过程如下：1)假设已知第n步的气膜压力分布，在求解第n+1/2步气膜压力分布的过程中，将轴承周向方向φ的偏导数∂S/∂φ作为未知数，而轴向方向λ的偏导数∂S/∂λ可以由第n步的气膜压力得到；2)在求解第n+1/2步时，则将λ的偏导数作为未知数，而φ的偏导数可以由第n+1/2步的气膜压力得到，进而完成一个迭代循环。完成上述循环后，将n+1步的解作为初值，开始下一次迭代计算。

求得所有节点的气膜压力后，得到轴承的气膜合力为

(4)

(5)

1.3 转子动力学方程及数值求解过程

对于GFB支承的有不平衡质量的刚性转子系统，若仅考虑转子的柱形涡动，静态平衡位置系统的动力学微分方程为

(6)

式中：M为转子质量。

转子在运动过程中遵循牛顿第二定律，即

Ma(x,y,t)=f(x,y,t)，

(7)

式中：a为加速度。

以x方向为例，采用Verlet算法对 (7) 式进行离散化处理，得到x方向的位移、速度、加速度的迭代关系式为

(8)

式中：v为速度；Δt为时间步长。

同理，可得到y方向的位移、速度、加速度的迭代形式。第n步转子的偏心距en和偏位角θn为

(9)

通过en，θn可以得到第n步的气膜厚度和气膜压力分布。

对于GFB-转子动力学系统，通过力的传递实现气膜流场-转子刚体运动的耦合。给定初始条件和预计算周期数后，通过计算初始位置的气膜压力，得到转子在气膜合力下的加速度，通过(8)式计算转子在下个时间步长的位置和速度。计算流程图如图2所示，具体步骤如下：

1)根据转子的初始偏心距、偏位角及初始速度计算该工况下的的气膜压力分布，对气膜压力积分，得到作用在转子上的气膜合力；

2)通过(7) 式计算转子的加速度；

3)通过(8)式计算转子的位移和速度；

4)将第3步计算得到的转子位移代入(9)式计算偏心距和偏位角，再计算气膜厚度和气膜压力分布，返回第1步。

重复上述步骤，得到转子运动参数的时间序列。

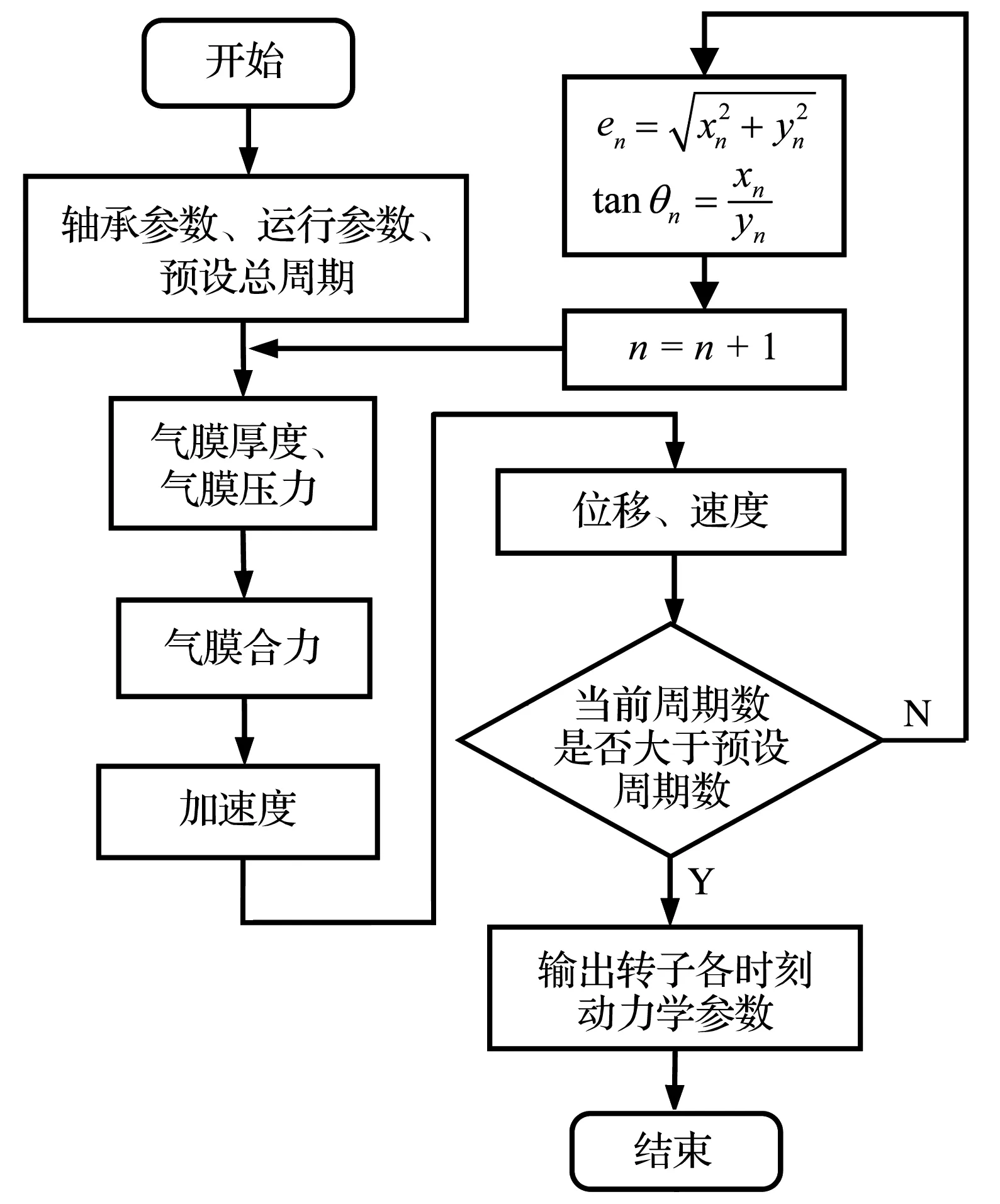
图2 计算流程图

2 动态特性系数计算

实际的GFB-转子系统是一个非线性系统，为了简化，可以将轴承的气膜力在静平衡位置附近线性化，即将轴承的承载力用8个线性化的刚度系数和阻尼系数刻画。

2.1 基于摄动法的动态特性系数

基于摄动法的动态刚度系数和动态阻尼系数计算公式为[7]

(10)

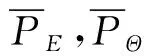
将(10)式的动态刚度系数和动态阻尼系数转化到直角坐标系中，得到动态刚度系数和动态阻尼系数为

(11)

式中：Kxx，Kyy为主刚度系数；Kxy，Kyx为交叉刚度系数；Cxx，Cyy为主阻尼系数；Cxy，Cyx为交叉阻尼系数。

2.2 基于轨迹法的动态特性系数辨识方法

2.2.1 线性简谐激振法

线性系统的输入和输出频率相同，非线性系统的输入和输出频率无确定关系。轨迹法实施过程如下：1)给定初始条件，进行流固耦合迭代计算，经过一段时间后转子处于静平衡位置；2)施加外激励，获得系统的响应；3)提取外激励的同频响应，根据同频率的输入和输出信号进行GFB的动态特性系数辨识。该方法相当于提取了GFB-转子系统的线性部分，被称为线性简谐激振法。

对转子施加角速度为ω1，空间相位差为90°的一组简谐激振力

(12)

从转子的位移响应中提取同频率的简谐振动

(13)

式中：A1,B1为简谐激振力的幅值；a1，b1为位移幅值。

转子的运动方程为

(14)

将 (12)，(13) 式代入 (14) 式可得

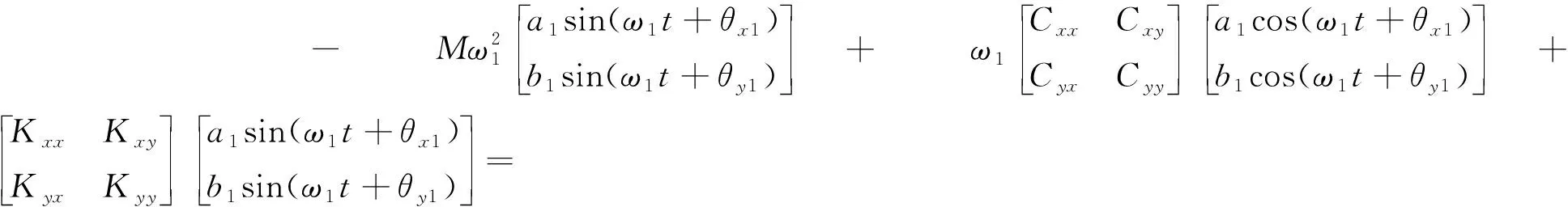
(15)

将 (15) 式展开，令两边的正弦项和余弦项的系数分别相等，可得

(16)

GFB的动态特性系数共有8个，一组激励仅能得到4个相互独立的方程，因此还需要另外一组激励。可采用表1的第1组和第2组激励。

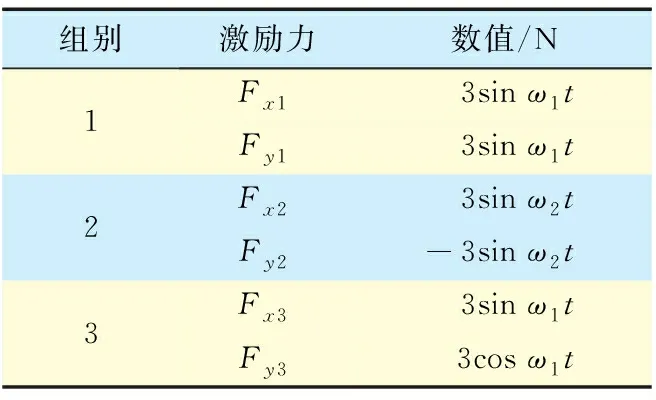
表1 外激励参数

轨迹法获得的转子位移信号x(t)可能含有除激励频率以外的其他频率成分，可表示为

(17)

式中：A0,a,b为任意常数。

若要提取响应中含ω1的成分，即计算a，b的值，对 (17) 式左右两边分别乘cosω1t，sinω1t并积分。以计算b为例

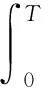
(18)

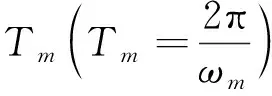
由三角函数的正交性可得

则由(18)式可得

(19)

同理可得

(20)

将转子位移信号x(t)代入 (19)，(20)式即可提取位移信号中含ω1的成分。

若第1,2组激励频率相同，即角速度ω1=ω2，可能会造成 (16) 式的系数矩阵接近奇异，在此将2组激励频率设置约50 Hz的差值，最后辨识出的动态特性系数应该是2组激励频率下的均值。

线性简谐激振法的缺点：1)需要2次激励，求得的动态特性系数是2组激励频率下的均值；2)仅考虑到激励频率的同频响应，忽略了其他涡动频率的影响。

2.2.2 简谐激振法

将轨迹法中每个时间步转子的位移、速度、加速度和气膜力代入(14) 式，可得到一个矛盾方程组，再通过最小二乘法即可辨识出8个动态特性系数。该方法可考虑所有涡动频率对动态特性系数的影响，相当于将非线性系统等效为线性系统，称之为简谐激振法。计算过程同2.2.1节，但仅需一次激励，在此选择表1的第3组激励。

在任意时刻τi(i=1，2，…，N)，无质量偏心的转子的运动方程可表示为

(21)

式中：Fgas_x,Fgas_y为作用在转子上的气膜力；Fx,Fy为作用在转子上的外激励。

若将气膜力等效为线性化的刚度系数和阻尼系数，则

(22)

将转子的自转周期T分为N步，时间步长τi=T/N,将轨迹法中每个时间步的位移、速度、加速度及气膜力代入(22)式，可以得到含8个未知数(动态特性系数)的N个方程。该方程是矛盾方程组，可以采用以Levenberg-Marquast(L-M)算法为基础的非线性最小二乘法求解，核心思想为：构造刚度、阻尼系数定义的等效力与数值计算的气膜力之间的误差，记为

(23)

式中：ei为第i个时间步的误差。

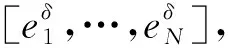
1)给定初始估计δ1、初始阻尼λ0及终止收敛条件ε，将δ1代入 (23) 式得到初始误差eδ1。

2)在初始值δ1的基础上再估计，构造增量方程，(22) 式的雅克比矩阵为

第2步的增量Δ为

(24)

式中：I为单位矩阵；λ为L-M算法的阻尼。

3)将δ2(δ2=δ1+Δ)代入 (23) 式，得到新的误差eδ2。若eδ2≤eδ1，eδ2≤ε时输出结果，否则，更新λk+1=λk/10，δ2=δ1，然后返回到第2步；若eδ2>eδ1，则更新λk+1=10λk，δ2=δ1，然后返回第2步。

重复上述步骤，直至得到满足收敛要求的δ。

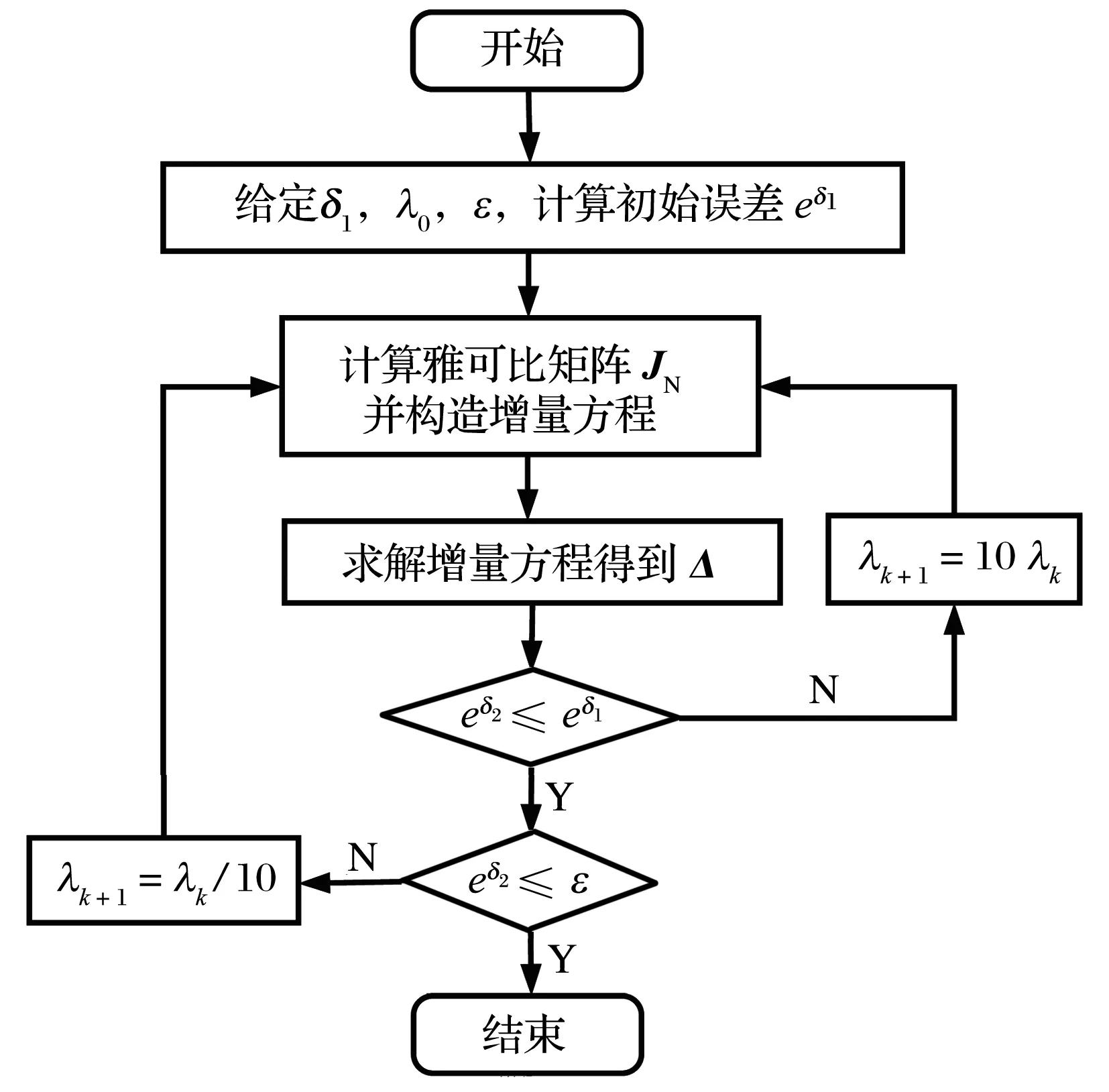
图3 L-M算法流程图

3 实例分析

以某气体箔片轴承为例分析，其主要结构参数及运行参数见表2。

表2 GFB的结构参数及运行参数

3.1 摄动法验证

本文的摄动法采用差分法数值求解，经分析网格划分的周向和轴向单位数分别为180，90时，GFB的动态特性系数与文献[7]的计算结果最接近，如图4所示，最大误差不超过3%，说明了本文摄动法计算模型的正确性。

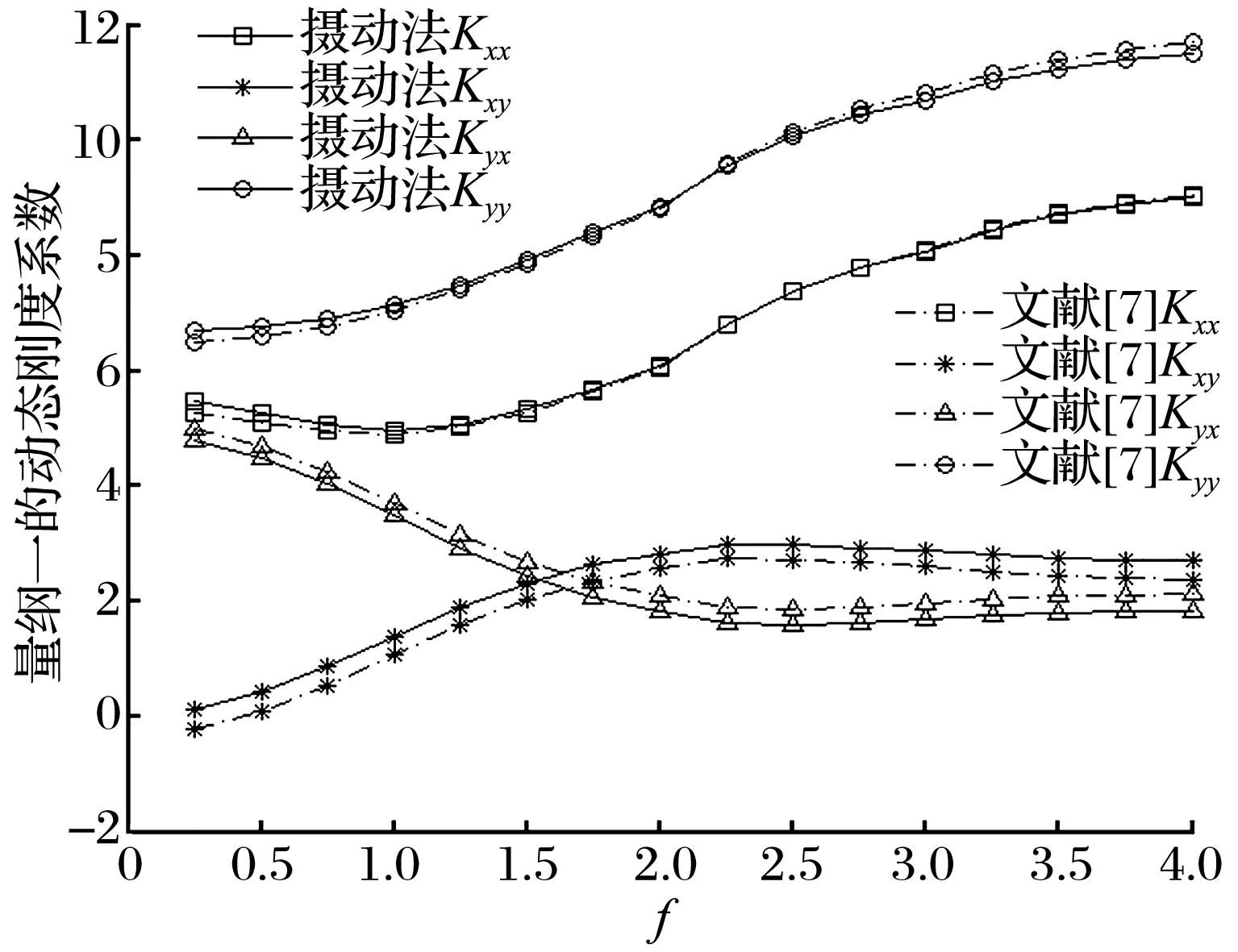
图4 e0=0.6时动态特性系数随扰动频率的变化趋势

3.2 轨迹法验证

无不平衡力、无外激励时的轴心轨迹如图5所示：转子由轴承中心下落后，经瞬态振动阶段后轴心轨迹收敛到狭长的椭圆轨道上。

图5 无不平衡力、无外激励时的轴心轨迹图

令ω1=300 Hz,ω2=350 Hz， 不平衡力为0，施加简谐激振力后的轴心轨迹如图6所示：转子在静平衡位置附近作不规则运动。x，y方向位移的时域响应如图7所示：施加外激励后转子的振动出现了多个波峰。x，y方向位移的频谱图如图8所示：转子存在5个不同的涡动频率，但主要为87.11，300 Hz的频率，其中300 Hz为外激励的同频响应。x方向位移的相图如图9所示：多个相点构成一个椭圆，说明系统此时作拟周期运动。将原始的位移数据分解为一系列三角级数之和， 这些三角级数重构的位移(2.2.1节(17)～(20)式)与原始位移数据的对比如图10所示：重构位移与原始位移曲线吻合，说明了轨迹法的正确性。

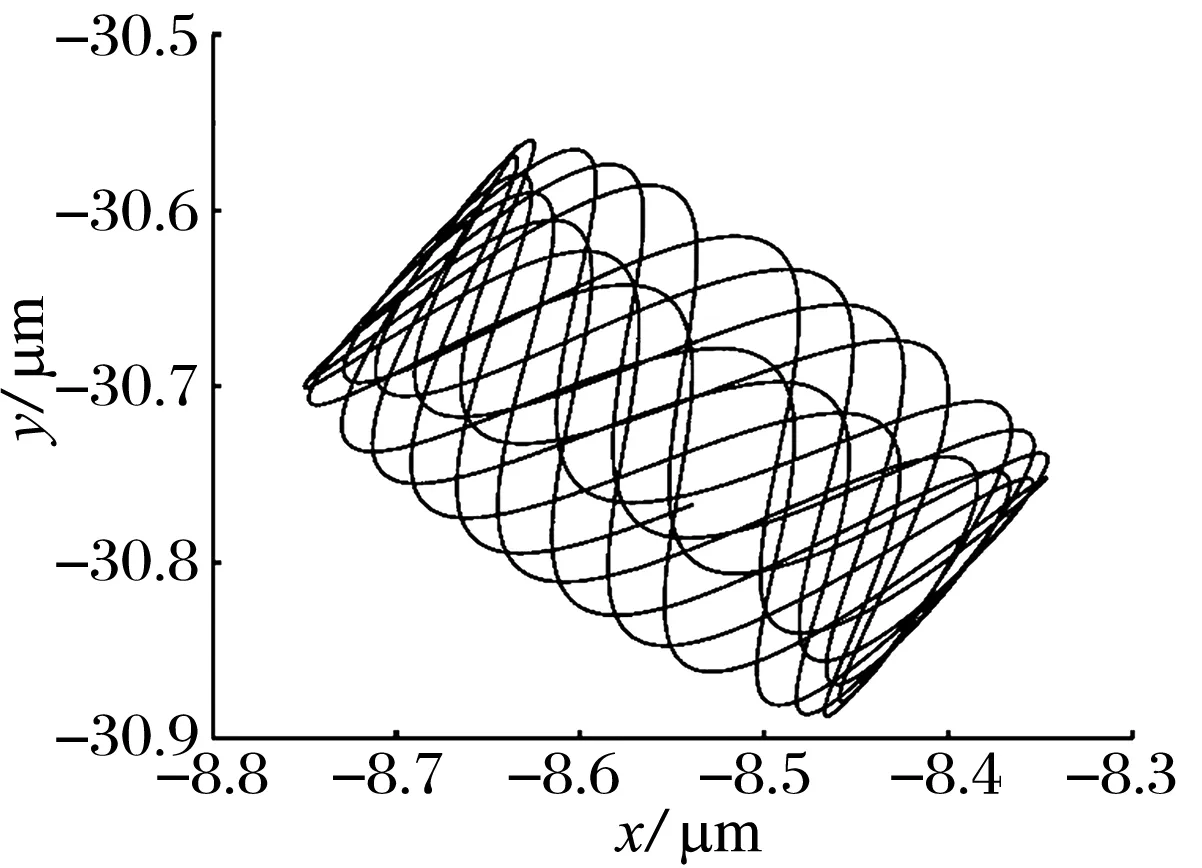
图6 无不平衡力、有简谐激振力时的轴心轨迹图

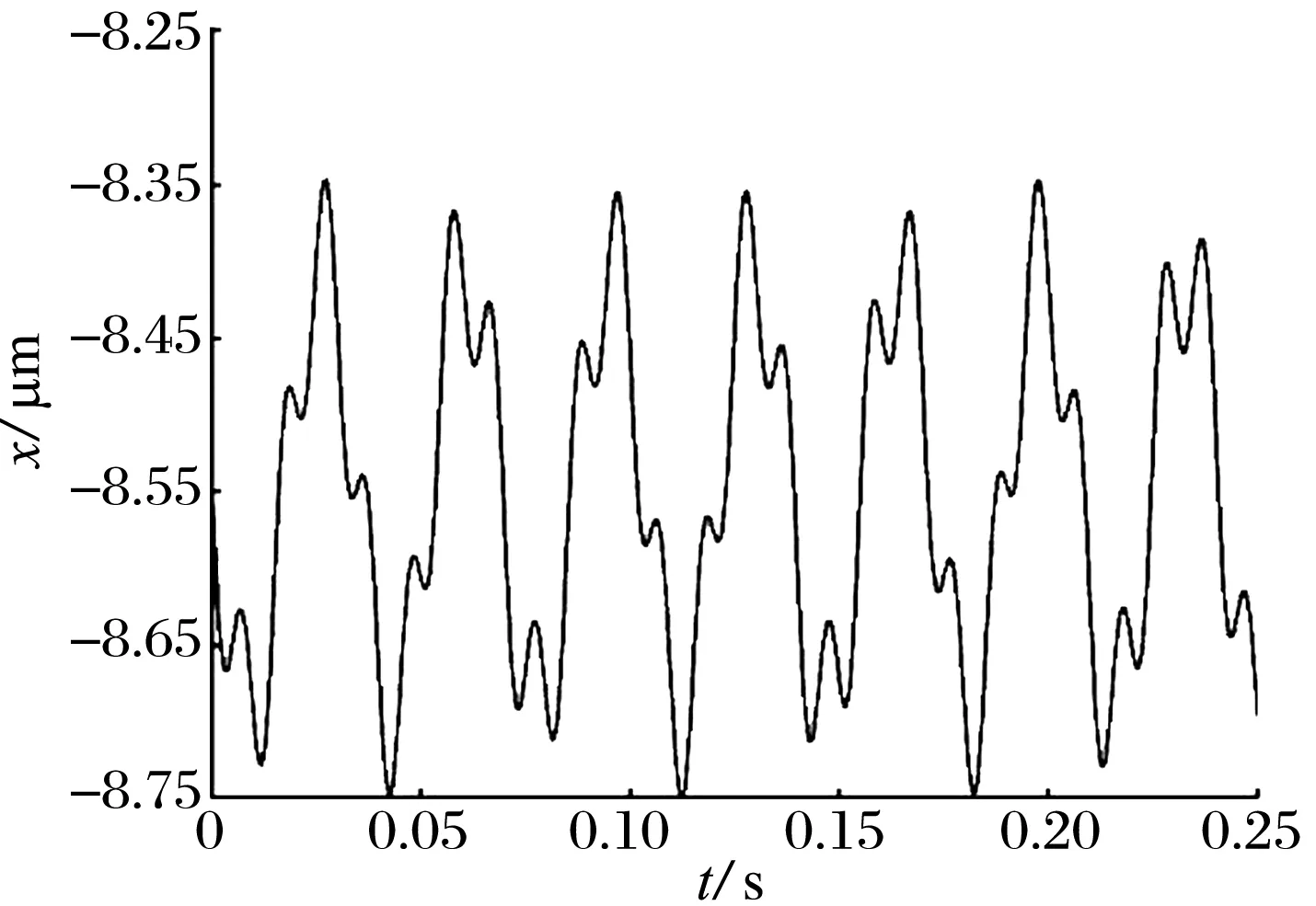
图7 时域图

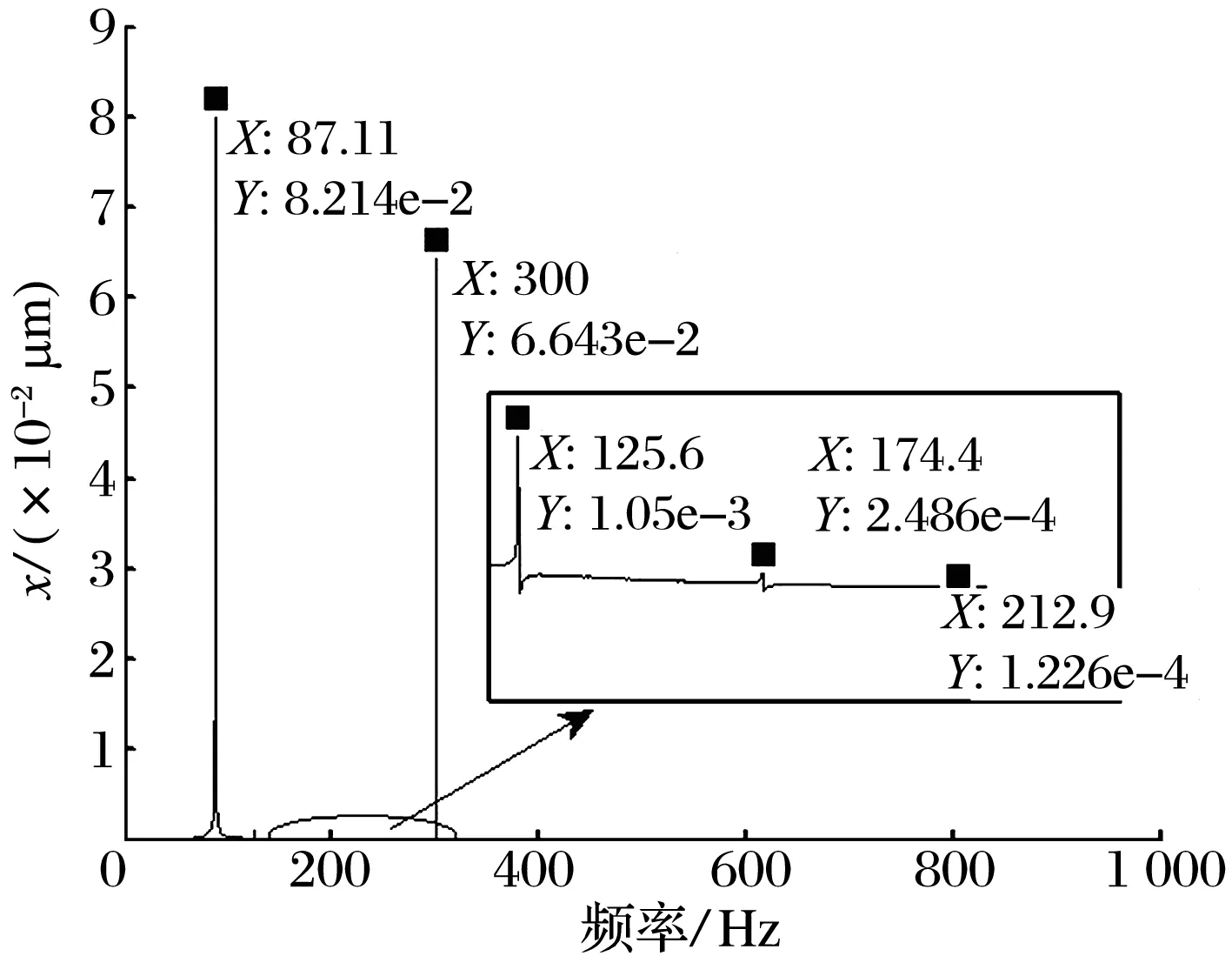
图8 频谱图

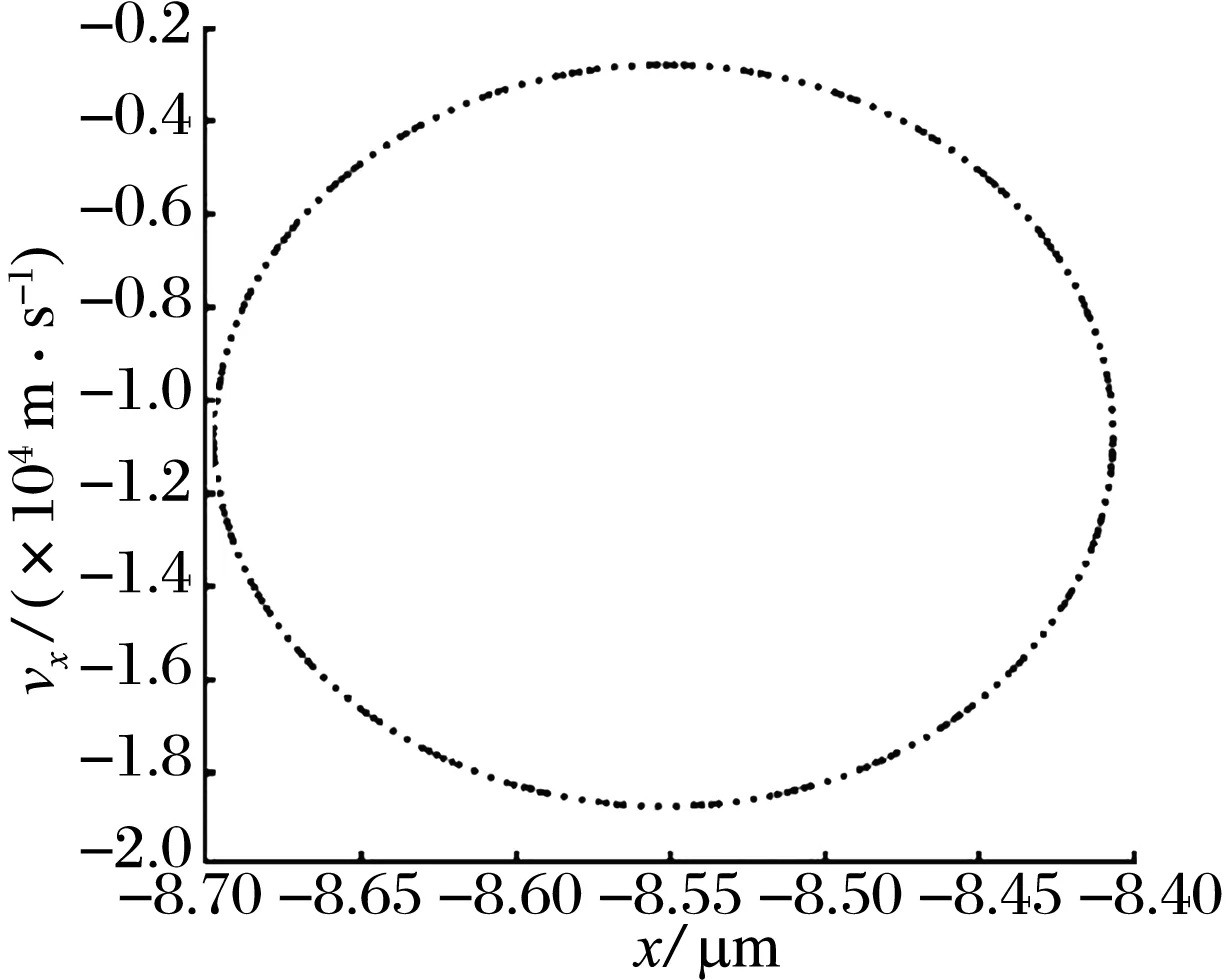
图9 x方向位移的相图

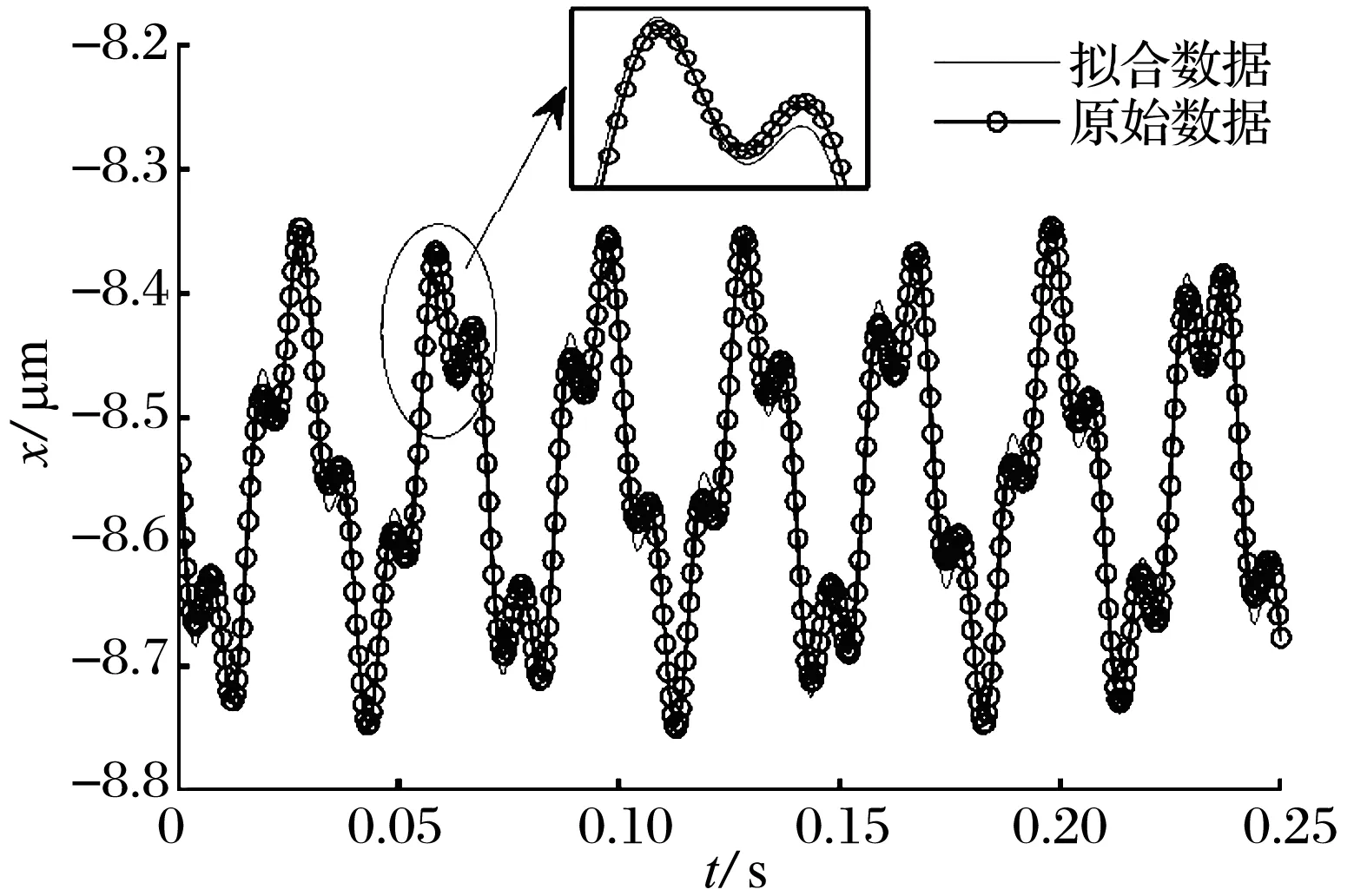
图10 位移的拟合数据与原始数据对比图

3.3 动态特性系数计算

摄动法、线性简谐激振法和简谐激振法动态特性系数计算结果见表3：1)不忽略交叉项的线性简谐激振法、忽略交叉项的线性简谐激振法、简谐激振法得到的主刚度系数Kxx分别为5.820×106，8.160×106，6.110×106N/m，与摄动法的相对误差分别为9.75%,24.13%,4.88%；2)不忽略交叉项的线性简谐激振法、忽略交叉项的线性简谐激振法、简谐激振法得到的主刚度系数Kyy分别为49.890×106，15.480×106，7.160×106N/m，与摄动法的相对误差分别为142.41%，28.75%，8.93%；3)摄动法、不忽略交叉项的线性简谐激振法、简谐激振法得到的交叉刚度系数Kxy，Kyx基本为同一个数量级；4)摄动法、线性简谐激振法、简谐激振法得到的主阻尼系数Cyy均为正，其他阻尼相差较大。本文提出的方法动态特性系数计算结果与摄动法均存在一定的差距，但对于气体箔片轴承在可接受范围之内。分析其原因为：摄动法仅考虑单一的涡动比，且仅保留了动态特性系数的线性项。线性简谐激振法考虑了多个涡动比，需要提取转子时域信号的幅值和相位进行参数辨识，同样仅保留了动态特性系数的线性项。简谐激振法考虑了多个涡动比，利用转子的时域信号进行参数辨识，无需提取幅值和相位，辨识出的动态特性系数虽然是等效的线性化系数，但能还原实际的气膜力，在某种意义上可以反映气膜力的非线性。

表3 GFB的动态特性系数

此外，简谐激振法根据转子的激励信号和响应信号可快速辨识出轴承的动态特性系数，无需求解静、动态雷诺方程，计算效率高。

4 结束语

基于轨迹法建立气体箔片轴承-转子系统的流固耦合动力学模型，求解简谐激励载荷下转子的瞬态轨迹，提出采用线性简谐激振法和简谐激振法辨识轴承的动态特性系数，线性简谐激振法仅考虑了外激励的同频响应，简谐激振法可考虑所有响应频率的影响。本文所计算的动态特性系数仍是线性化的，不能准确描述GFB-转子系统的非线性特性，模型需进一步完善。