可倾瓦径向节流器静态特性的仿真分析

王志成，刘雨航,2，沈小燕，白科研，李东升

(1.中国计量大学 计量测试工程学院，杭州 310018；2.杭州海康威视数字技术股份有限公司，杭州 310051)

1 概述

相对于传统的滚动轴承和滑动轴承，气浮轴承因高精度，低功耗， 小磨损，无污染等优点而广泛应用于超精密加工与检测等领域[1-2]。气浮轴承按照其基本结构形式可划分为止推轴承和径向轴承，按照供气节流方式可分为整体式和分体式。可倾瓦径向气浮轴承是一种典型的分体式轴承，由于具有良好的稳定性和承载能力，在高速旋转机械中得到广泛应用[3]。

可倾瓦气浮轴承一般由多个可绕其枢轴自由旋转的轴瓦节流器组成，通过调整轴瓦节流器数量和摆放角度θ，实现对旋转主轴的固定与支承，其结构如图1所示。当主轴在载荷作用下发生偏移时，各轴瓦会根据载荷调整气膜厚度，产生相应的气膜压力(承载力)保证平衡，从而达到稳定状态[4]。

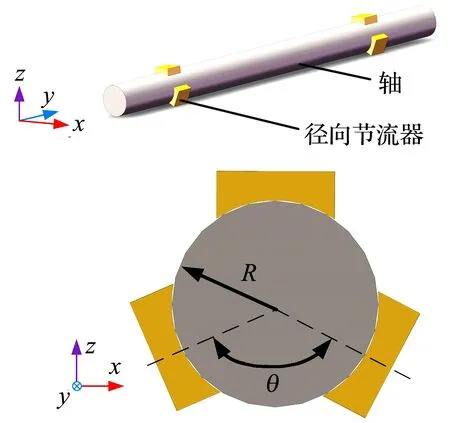
图1 可倾瓦径向气浮轴承轴系结构示意图

国内外学者对可倾瓦轴承的静态性能进行了广泛研究：文献[5-6]对可倾瓦气浮轴承的静态性能进行了分析，得到了不同组合参数下的静态性能曲线；文献[7]从偏心距、预紧力、轴承数对三轴瓦可倾瓦气浮轴承的静态性能进行了理论分析；文献[8]通过数值模拟研究了气流模型及回流材料对可倾瓦轴颈轴承静态性能的影响，发现具有低雷诺数校正的剪切应力模型及空气回流材料更适合可倾瓦轴颈轴承的数值模拟；文献[9]基于COMSOL模拟软件研究了不同偏心率、轴瓦间隙、轴瓦数量等因素对可倾瓦轴承性能的影响；文献[10]对可倾瓦径向气体轴承的静、动态特性进行了数值求解，认为轴承数和轴颈偏心率对轴承的静、动态特性影响较大；文献[11]采用有限差分法求解了可倾瓦径向气体轴承的气体润滑方程，并研究了轴承间隙对可倾瓦轴承静态性能的影响。上述文献的研究主要侧重于轴承间隙、轴承数、偏心率等对静态性能的影响，很少结合均压槽、节流孔孔径等结构参数进行研究。

本文通过建立单个可倾瓦径向节流器气膜流域的仿真模型，研究均压槽槽深、槽宽、槽长、节流孔孔径、偏心率和供气压力对可倾瓦径向气体静压节流器承载能力、刚度的影响。

2 可倾瓦径向节流器

2.1 节流器结构

可倾瓦径向节流器结构如图2所示，节流器上表面为40 mm×40 mm的正方形，节流方式为小孔节流。气体以一定的供气压力Ps由进气口进入，经过节流器内部气腔从节流孔(孔径d)流出进入气膜间隙向四周扩散，在径向节流器与主轴之间形成稳定的润滑气膜，最后气体在径向节流器边缘排出，外部为大气压力Pa，φ为单个径向节流器工作面对应的圆心角(70°)，主轴半径R为35 mm。

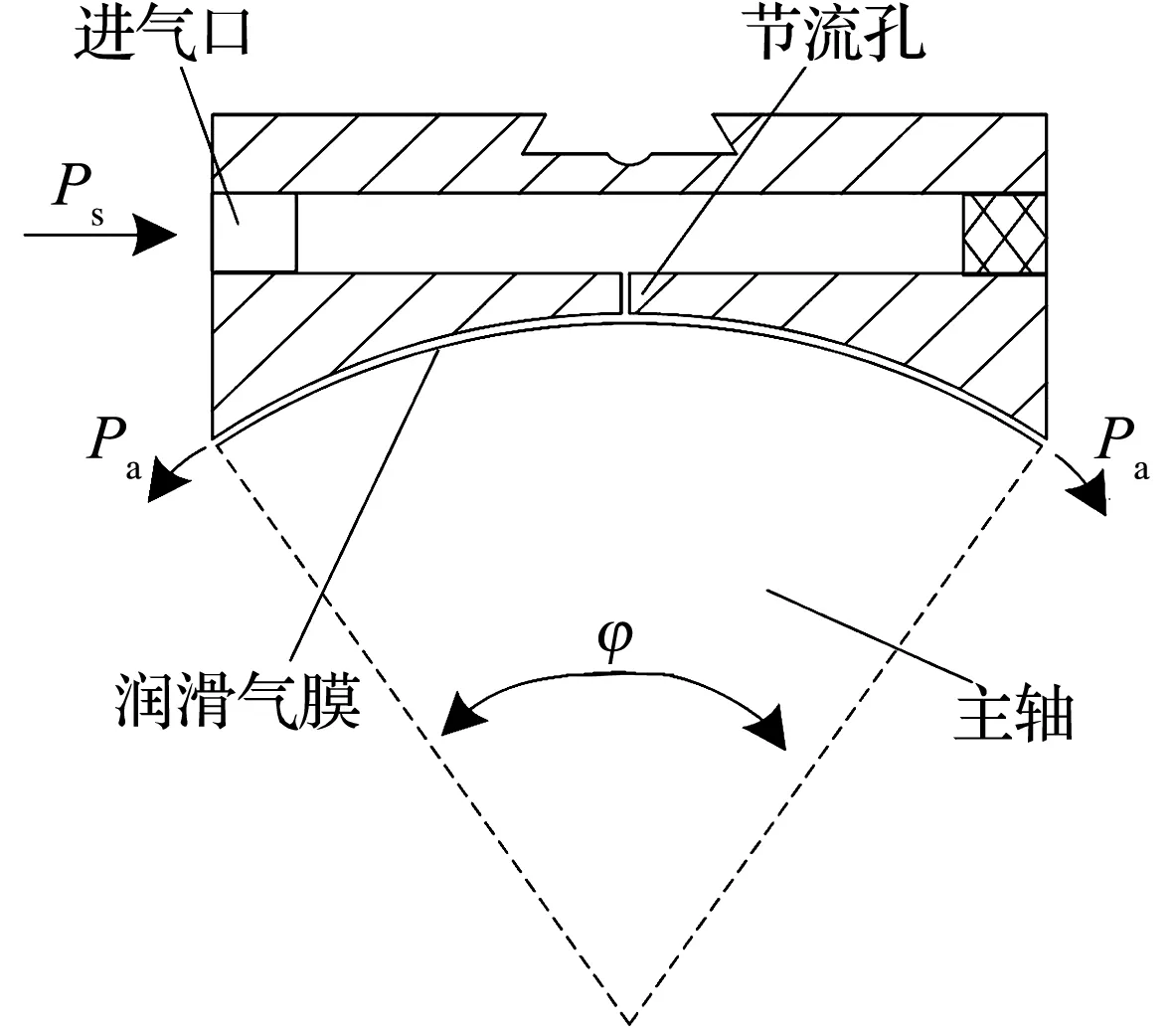
图2 可倾瓦径向节流器结构示意图

2.2 节流器的承载力和刚度

单个节流器的承载力和刚度可采用气体润滑控制方程描述。主轴与节流器之间曲面润滑气膜满足雷诺方程，即

(1)

则节流器的承载力与刚度为

(2)

(3)

式中：ρ为气体密度；h为气膜厚度；μ为气体动力黏度；p为润滑气膜上的压力；U为轴颈表面周向速度；t为时间；a为径向节流器的轴向宽度。

承载力和刚度的计算较为复杂，传统的求解方法难以实现，计算机技术的快速发展以及在流体力学中广泛使用数值计算方法使得承载力、刚度等静态参数的精确求解得以实现。本文采用流体仿真软件COMSOL求解润滑气膜雷诺方程[9]867，从而得到节流器静态性能随均压槽尺寸的变化规律。

3 可倾瓦径向节流器仿真建模

3.1 模型建立及网格划分

为研究节流孔孔径、偏心率、供气压力、气膜厚度对单个可倾瓦径向节流器静态性能的影响，将图1中单个可倾瓦径向节流器进气孔到轴承间隙出口的气体流场作为研究对象[9]868，使用COMSOL仿真软件建立仿真模型1如图3a所示；为研究均压槽结构参数对节流器静态性能的影响，考虑加工与网格划分难度，在节流器工作面的节流孔处开一轴向均压槽，长度为节流器轴向长度的一半，带均压槽的流域仿真模型2如图3b所示。

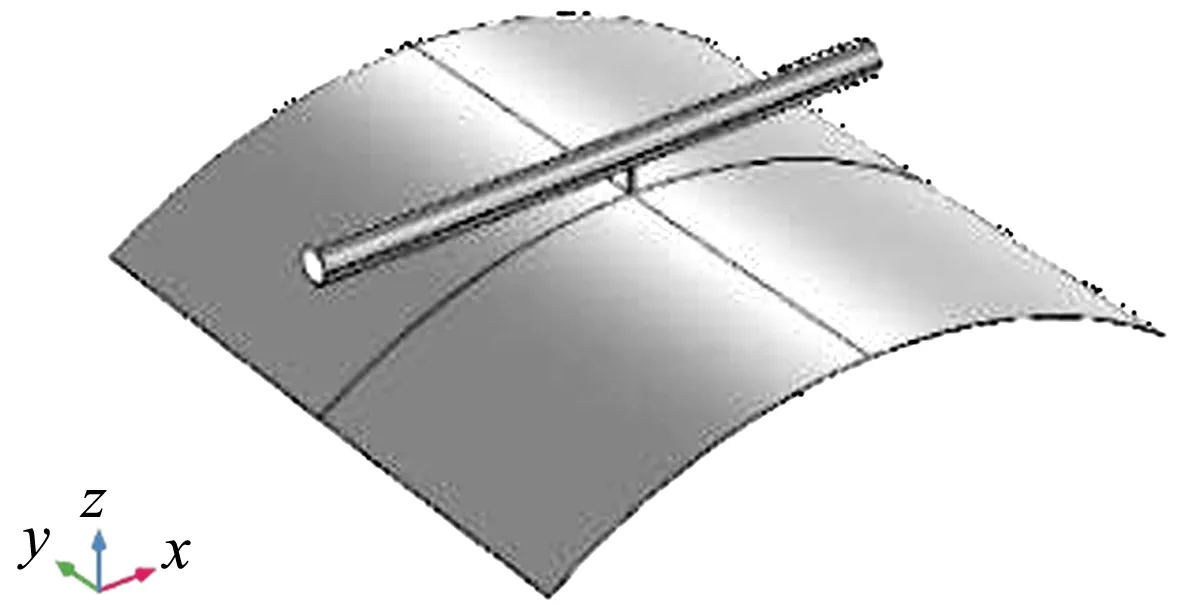
(a)无均压槽

由于在数值计算过程中不可能做到网格之间相互独立，需要进一步讨论网格尺寸。设定供气压力为0.5 MPa、气膜厚度为5 μm、偏心率为0，使用图3a仿真模型计算不同网格尺寸下的承载力变化，如图4所示。

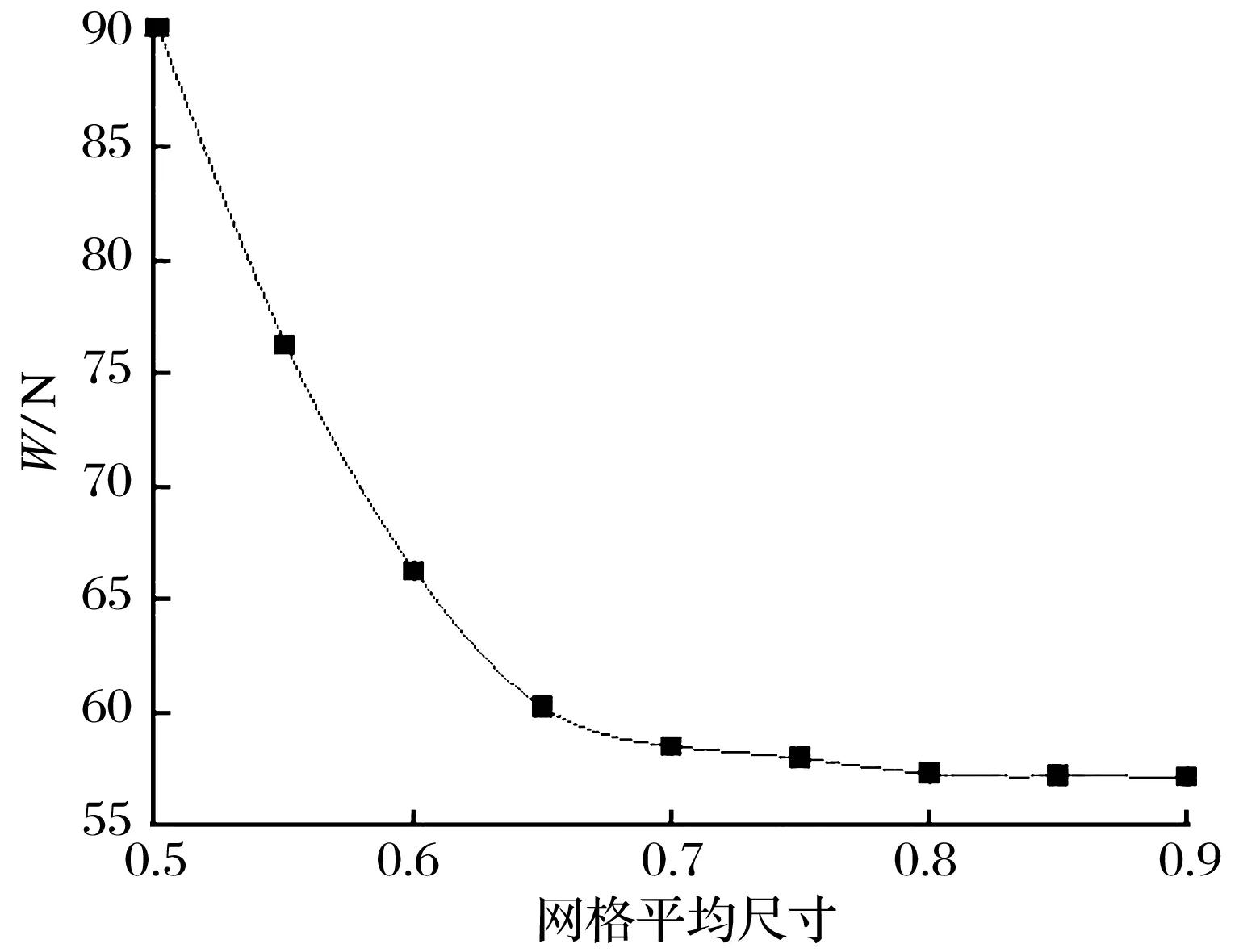
图4 网格平均尺寸对承载力的影响

由图4可知，当网格平均尺寸达到0.78时，承载力不再变化。在相同条件下对有均压槽的模型进行计算，承载力随网格平均尺寸的变化曲线与图4几乎一致，网格平均尺寸收敛于0.77左右。最终确定使用自由三角形网格和扫掠相结合的方式进行网格划分，并在节流孔与均压槽处采用网格极细化(网格尺寸为0.008)，气膜其他区域网格超细化(网格尺寸为0.06)，并对气膜厚度方向上进行分层处理，最终得到平均网格单元尺寸均在0.78以上，网格划分结果如图5所示。

(a)无均压槽

3.2 边界条件及参数设置

添加材料为空气，材料属性默认选择；物理场选择流体流动中非等温流动的湍流模型，选择稳态研究；设置1个进气面为入口压力条件，4个出气面为出口压力条件(大气压)，其他面为无传热无滑移的壁面；环境温度设置为298.15 K。

采用控制变量法，针对不同节流器静态性能影响因素进行多组仿真，每组仿真的具体参数设置见表1。其中， 槽深Gd步进0.05 mm， 槽宽Gw步进0.05 mm，槽长Gl步进3 mm，孔径d步进0.05 mm，偏心率步进0.1，供气压力Ps步进0.05 MPa。

表1 每组仿真变量及其参数设置

4 可倾瓦径向节流器承载力与刚度的影响因素分析

4.1 有无均压槽

为研究均压槽对可倾瓦径向节流器承载力和刚度的影响，分别采用模型1，2在相同的初始条件下进行仿真计算，均压槽对承载力和刚度的影响曲线如图6所示，均压槽使得气膜流域内的气体压力得到了更好的保持，明显提高了节流器的承载力。

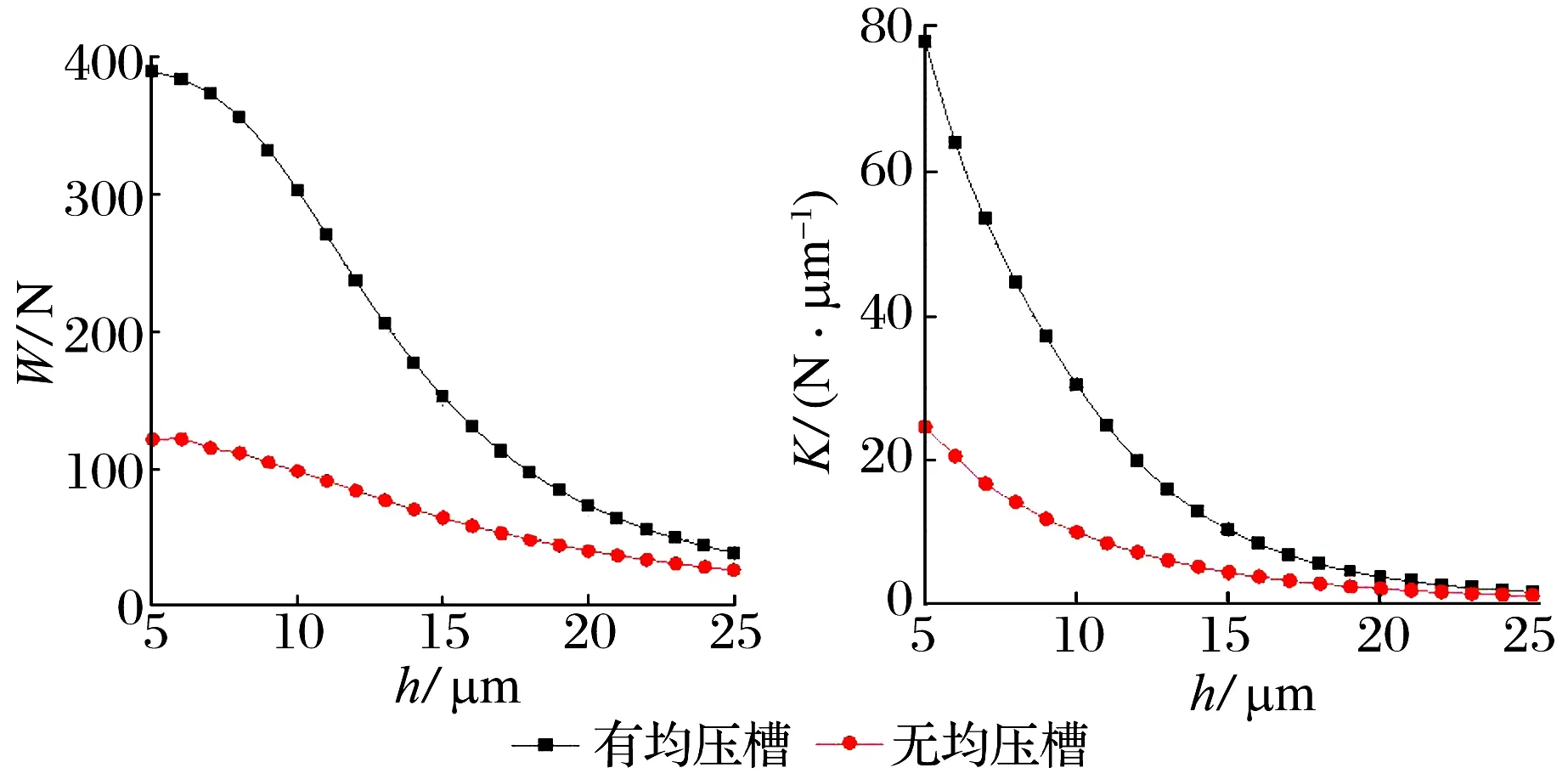
图6 均压槽对承载力和刚度的影响

4.2 均压槽深度

不同均压槽深度对径向节流器承载力和刚度的影响如图7所示：槽深小于0.2 mm时，承载力和刚度随着槽深的增大而迅速增加，当槽深大于0.2 mm时，承载力和刚度随槽深变化不明显。产生这种现象的原因主要是压缩气体从节流孔进入润滑气膜时，压力下降速度随着均压槽深度变大而变慢，提高了高压气体的利用率，从而增加了润滑气膜的承载力和刚度；当槽深增加到一定程度时，压力下降，速度保持稳定，对承载力的影响逐渐变小。

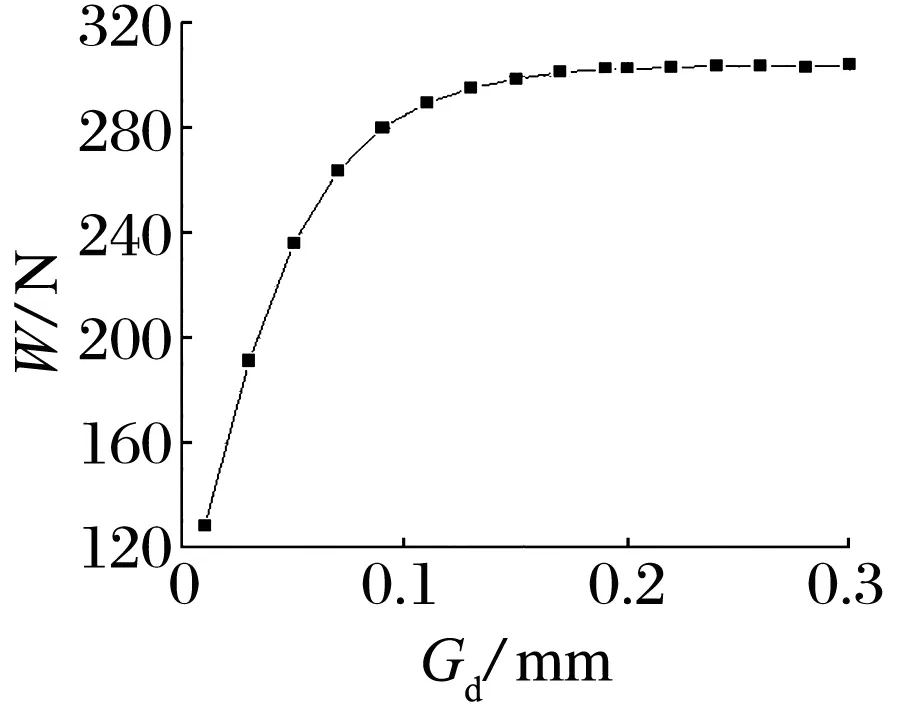
图7 均压槽深度对承载力和刚度的影响

4.3 均压槽长度

不同均压槽长度对径向节流器承载力和刚度的影响如图8所示，在气膜厚度较小时(5～10 μm)，承载力和刚度随着均压槽长度的增加而增大，原因为在气膜间隙较小时气体主要通过节流孔进入均压槽，再由均压槽进入气膜，线性供气效果明显，节流器有均压槽区域的压力得到了较好的保持，从而提高了承载力与刚度。

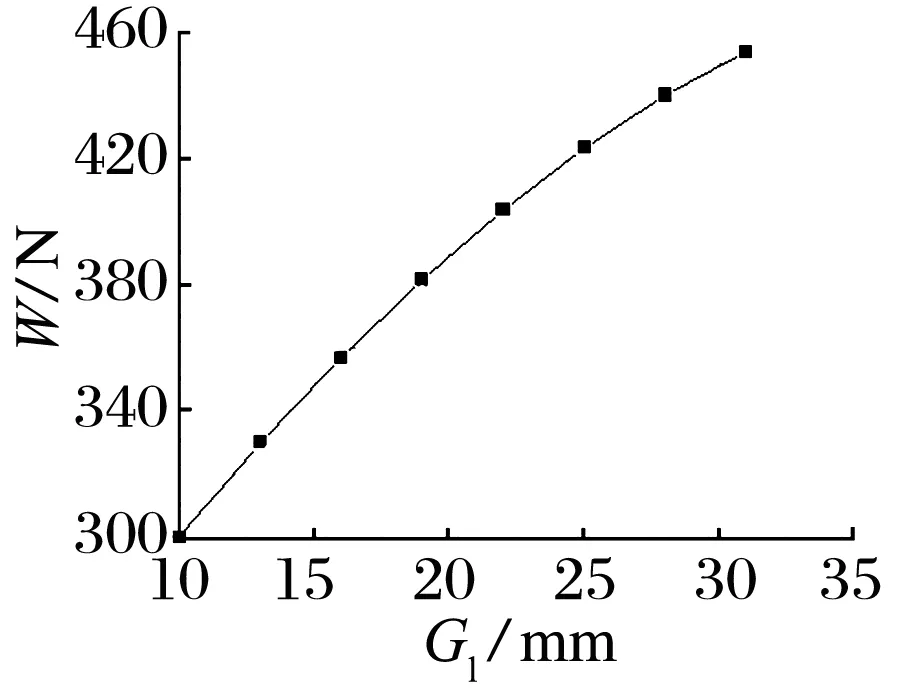
图8 均压槽长度对承载力和刚度的影响

4.4 节流孔孔径

以供气压力0.5 MPa为例，不同节流孔孔径下的压力分布如图9所示：节流孔处的气膜压力最大，且孔径为0.25 mm时的节流孔处气膜压力为最大值。不同供气压力下节流孔孔径对承载力和刚度的影响如图10所示：径向节流器承载力随着节流孔孔径的增大先增大后减小，节流孔孔径为0.25 mm时承载力最大；节流器刚度随着节流孔孔径的增大先减小后增大，孔径为0.25 mm时刚度最小。

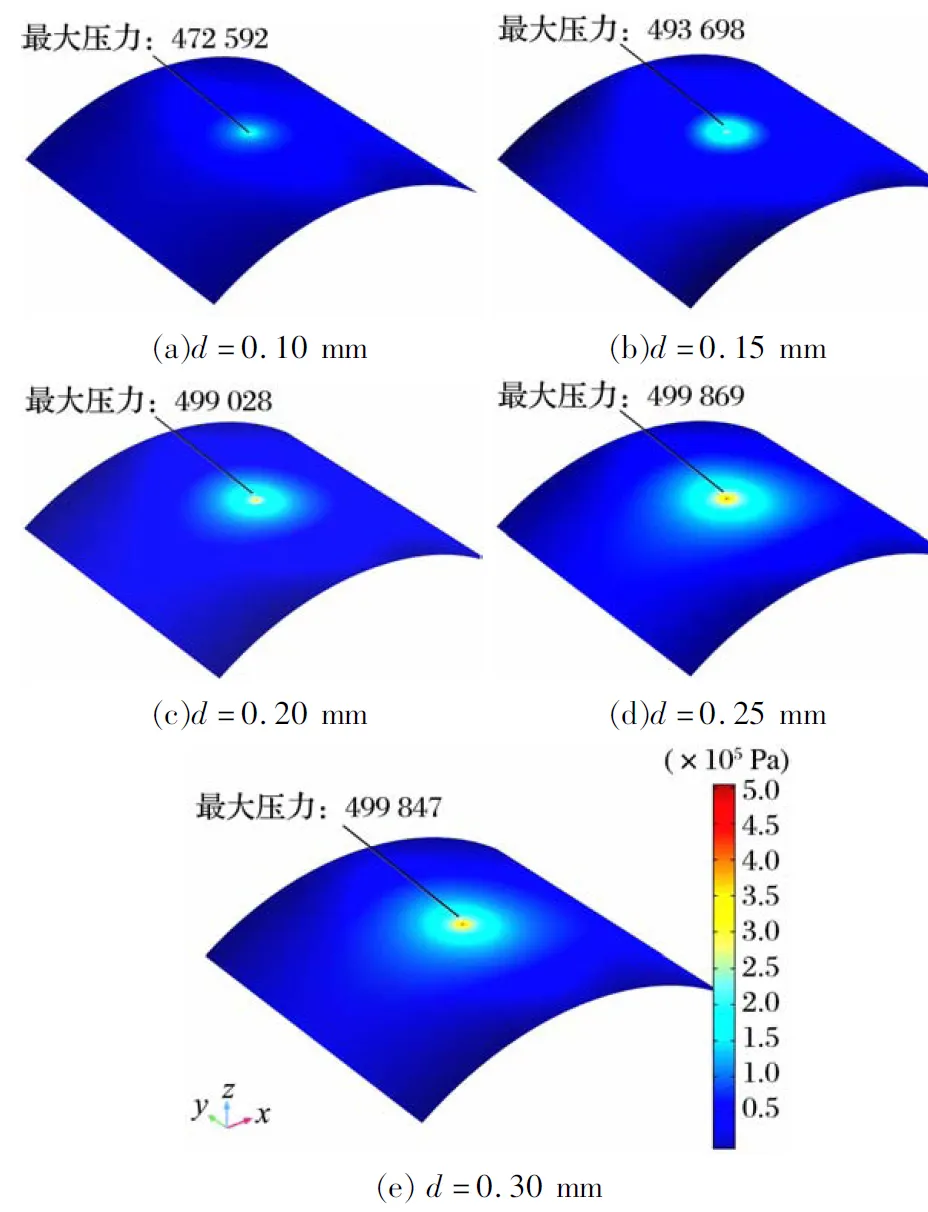
(e) d=0.30 mm

由上可知，节流孔孔径是影响气膜承载力和刚度的重要因素，节流孔孔径过小，会导致气膜承载力不足；节流孔孔径过大，节流效应降低， 导致气膜刚度在较大间隙时衰减：因此，可倾瓦节流器节流孔一般为0.1～0.2 mm。

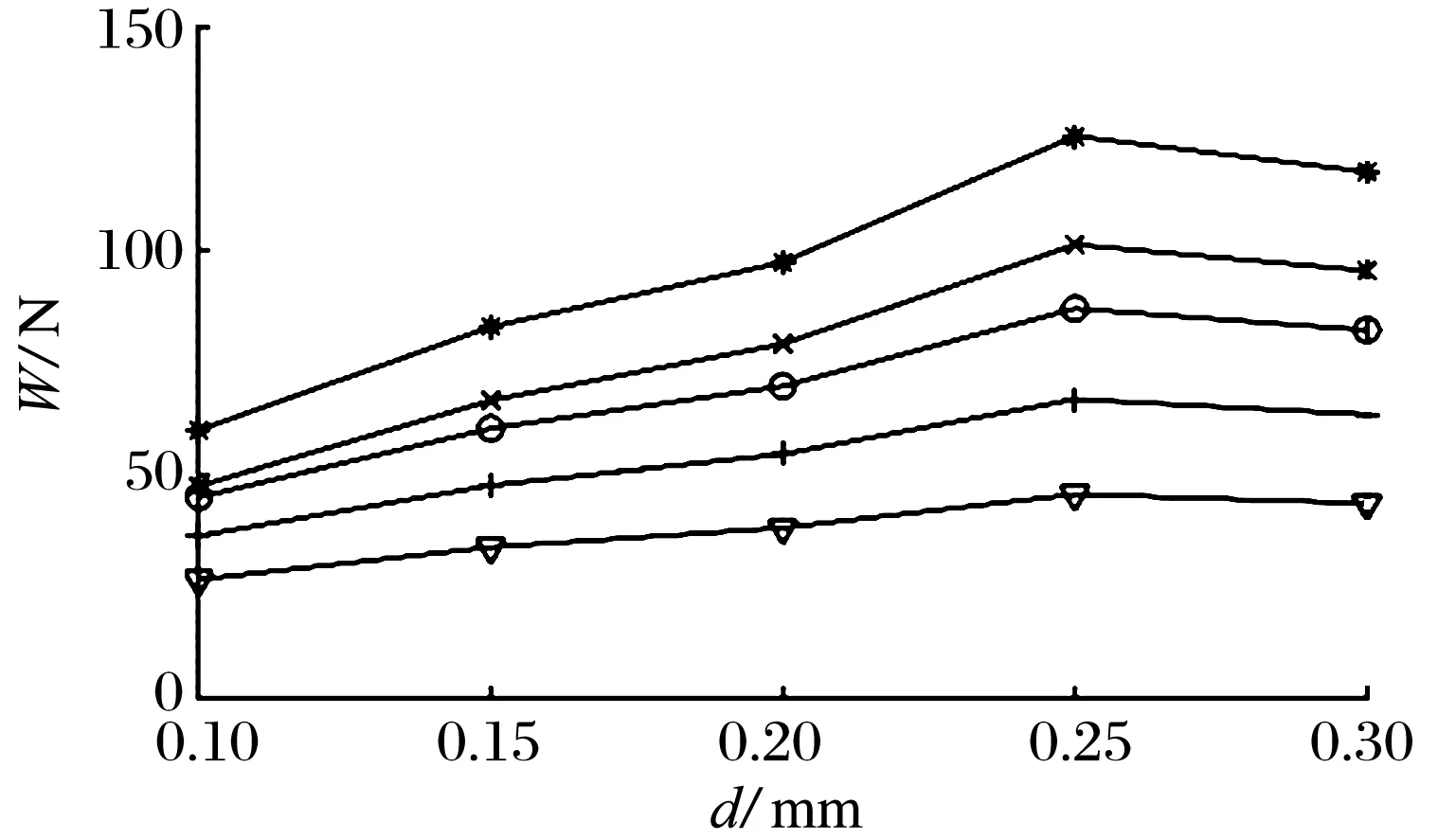
图10 节流孔孔径对承载力和刚度的影响

4.5 均压槽宽度

在满足Gw>d的条件下，Gw分别为0.20，0.25，0.30，0.35，0.40 mm时节流器的承载力与刚度如图11所示：随着均压槽宽度的增加，节流器承载力和刚度的变化不显著，说明均压槽宽度对节流器承载力和刚度影响较小。

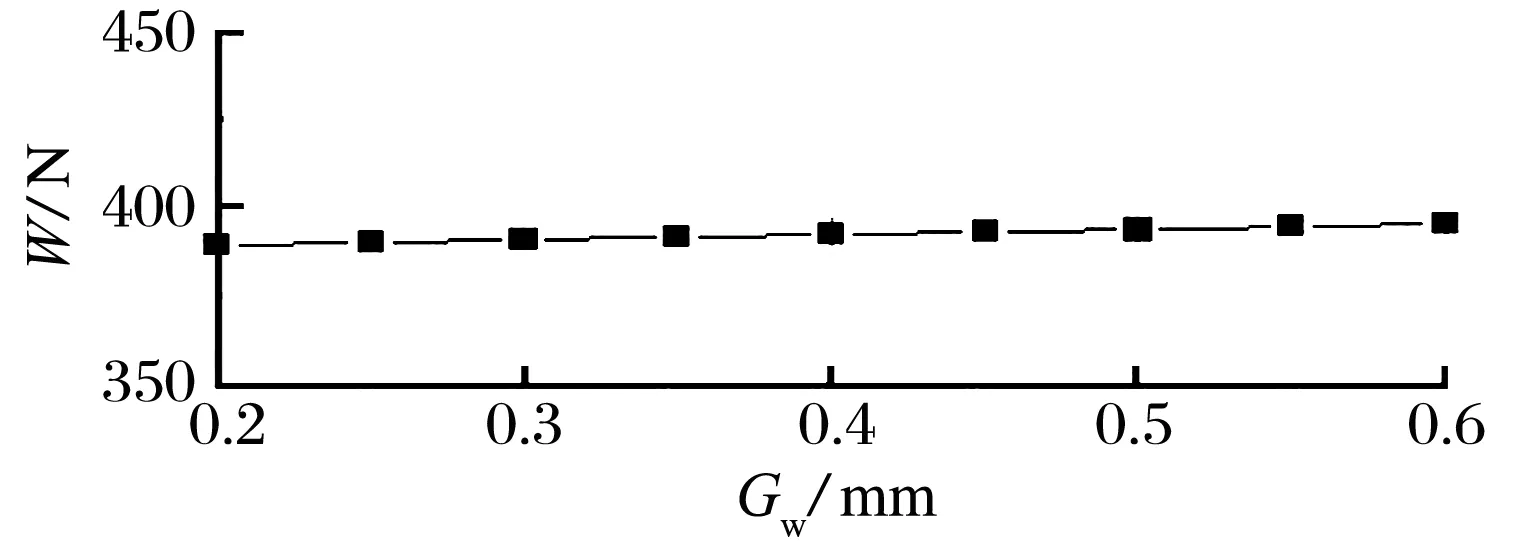
图11 均压槽槽宽对承载力和刚度的影响

4.6 偏心率

偏心率为转轴中心偏离轴承中心的距离与气膜间隙的比值。在不考虑均压槽的情况下，偏心率在不同供气压力下对径向节流器承载力和刚度的影响如图12所示。节流器承载力随着偏心率的增大先增大后减小，偏心率0.4左右时承载力最大；节流器刚度总体趋势随偏心率的增大而减小，偏心率0.8左右时刚度最小：因此，对于可倾瓦径向节流器，最佳偏心率范围为0.1～0.5，可根据实际承载力和刚度需要做出具体调整。

图12 偏心率对承载力和刚度的影响

4.7 供气压力

以气膜厚度为10 μm为例，不同供气压力下的气膜压力分布如图13所示，不同供气压力对径向节流器承载力和刚度的影响如图14所示：随着供气压力的不断增加，节流器的承载力和刚度显著提升。

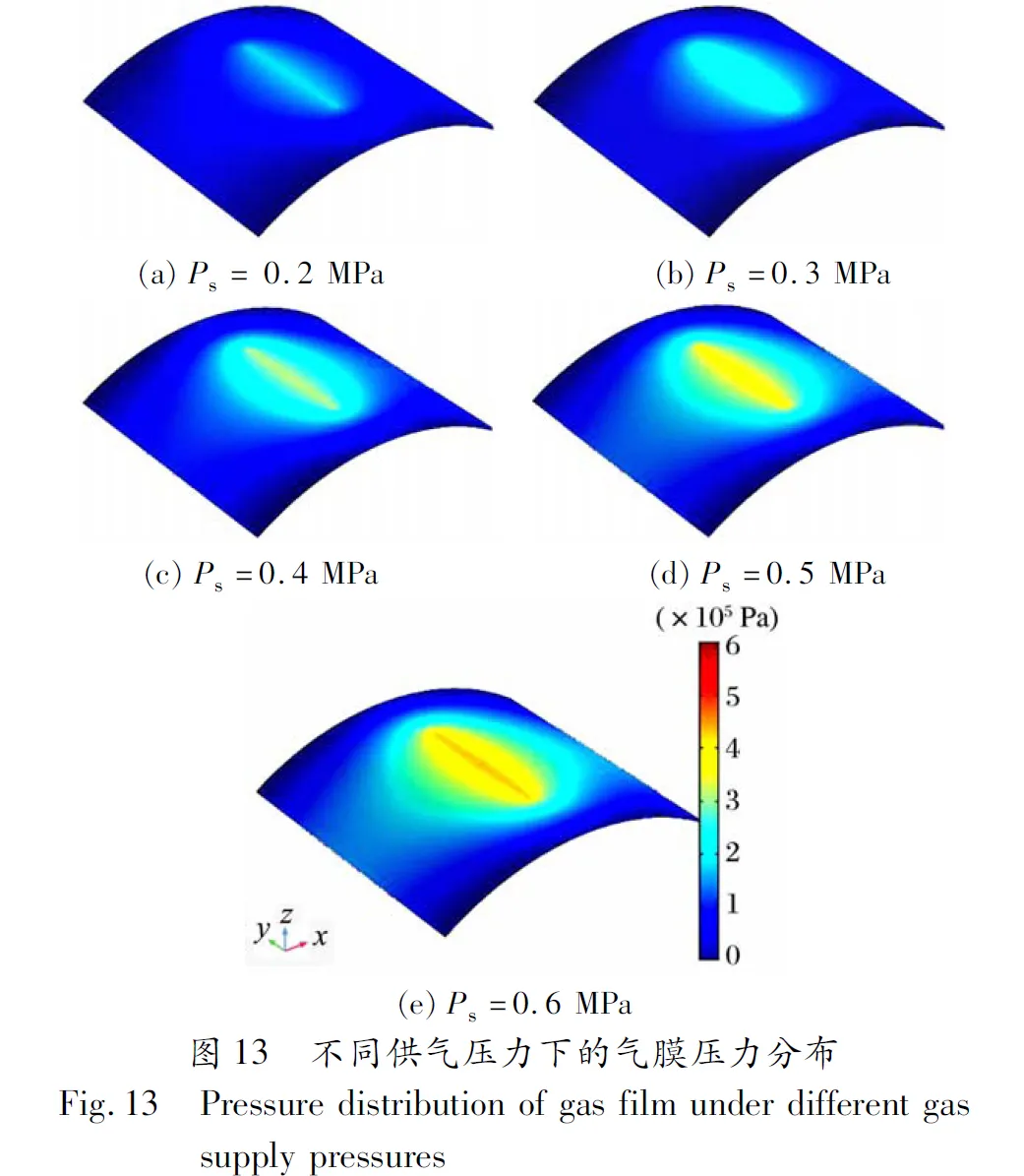
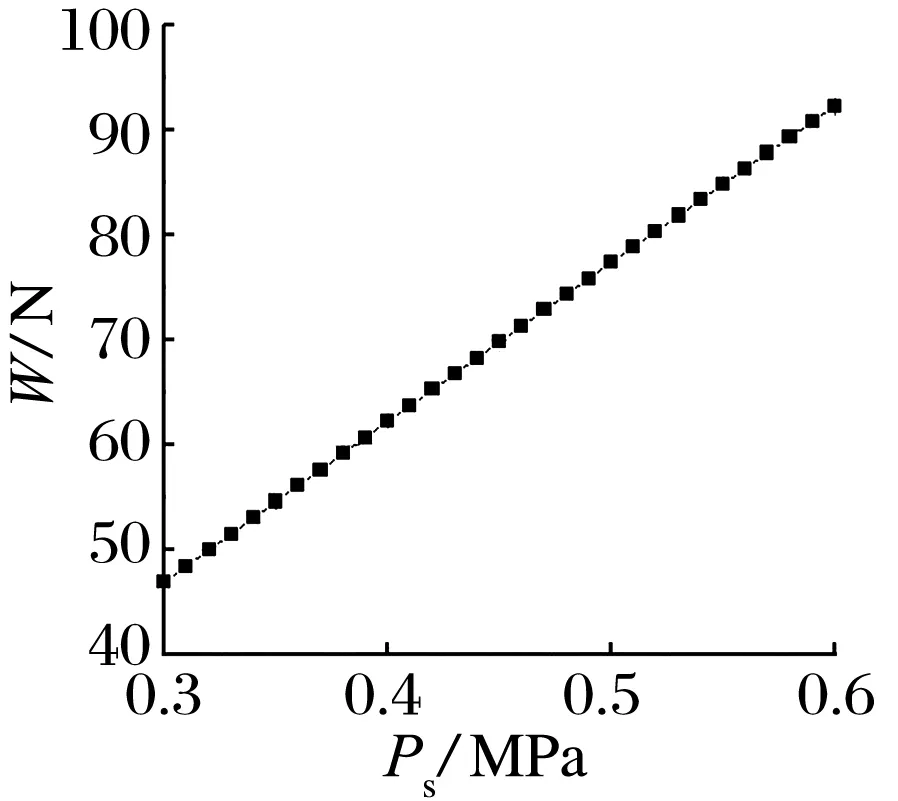
图14供气压力对承载力和刚度的影响

5 结论

仿真分析了单个可倾瓦节流器的结构参数和供气压力对节流器静态性能的影响，得到如下结论：

1)均压槽能够明显提高节流器的承载能力；在气膜厚度较小(5～10 μm)时，增加槽长可以明显提高承载力和刚度；槽深大于0.2 mm和槽宽为0.2～0.6 mm时，对节流器承载力和刚度的影响效果均不显著。

2)承载力和刚度随着供气压力的增大而增大；承载力随偏心率(0～0.9)、节流孔孔径(0.1～0.3 mm)的增大表现为先增大后减小，刚度表现为先减小后增大。