数形相依 化繁为简
2022-10-20余敏霞
余敏霞


[摘 要] 数形结合的思想作为数学最重要的思想之一,将抽象的数字转化成清晰易懂的图形,多维度地提供问题的解决思路,沟通数字与图形之间的关系,实现问题解决的简单化。研究者结合二年级数学,探索“数形结合思想”在问题解决中的實际应用。
[关键词] 问题解决;数形结合;解决措施
马克思曾经说过:数学是空间形式与数量关系相结合的一门学科,它是以自然科学为基础的,解释自然和社会规律的科学。可见数学就是对于“数”和“形”的研究。数形结合思想是将直观的空间形式和严谨的数量关系相结合来认识数学,利用“数”与“形”的优势进行互补,使抽象的问题变得更加具体,复杂的问题变得更加简单[1]。因此,在小学阶段进行数形结合思想的渗透,引导学生利用数形结合思想解决问题显得非常必要。笔者结合二年级数学,探索“数形结合思想”在问题解决中的实际应用。
一、由形及数
1. 依托形,计算数
初学计算过程中,学生对于计算还不是很熟悉,教师往往需要利用小棒帮助学生进行计算。从20以内的加减法、100以内的加减法、乘法、除法到有余数的除法的过程中,学生初次进行计算时,往往要借助小棒。而在有余数的除法计算中,学生则需要利用小棒摆出图形帮助解决。
案例1 “有余数的除法”教学片段
片段一
师(课件动态演示分草莓的过程,如图1):你们看到了什么?
生:7个草莓摆成了3盘,每盘2个,还多了1个。
师:你们能用一个算式表示出来吗?
生:7÷2=3(盘)……1(个)。
师:3表示什么意思?1表示什么意思?
片段二
师:用8、9、10、11、12根小棒摆正方形,你能用算式表示出来吗?
生:8÷4=2(个);
9÷4=2(个)……1(根);
10÷4=2(个)……2(根);
11÷4=2(个)……3(根);
12÷4=3(个)。
师:为什么不能多余4根小棒呢?有没有同学上来动手做一做?
师(总结):通过小棒操作,学生理解4根小棒可以拼成一个正方形。
面对一个新的问题,学生仅仅通过理解题意来解决是有困难的。因此教师需要借助小棒解决问题,而在第二个问题中,仅靠小棒还不够,还要将小棒拼成正方形(如图2),利用图形解决问题。教师在解决问题的过程中,要对学生进行引导,帮助解决问题。
2. 依托形,解决数的问题
学生在解决问题过程中,由于有时不能对图形信息进行加工、分析,解决问题的策略不能得以优化,故在教学过程中,教师要引导学生对图片信息加以整理、分析。
案例2 “有余数的除法解决问题”教学片段
师:按照下面的规律摆小旗(如图3)。这样摆下去,第16面小旗应该是什么颜色?
生:我是用算一算的方法来完成的,用16除以3等于5组余1面。我是这样想的,这道题是算16面小旗里有几个3,所以用除法来解决。每3面小旗一组,所以要用16除以3,商是5,余数是1,表示是下一组里面的第一面,就是黄色的小旗。
师:16表示什么?3表示什么?5表示什么?1表示什么?
生:16表示总共有16面小旗,3表示每组里面有3面小旗,5表示有这样的5组小旗,1表示下一组里面的第一面小旗。
师:第27面小旗应该是什么颜色?
有的学生发现27÷3=9没有余数,该怎样判断呢?
小结:余数是几,答案就是这一组中的第几个。没有余数说明正好分完,就是每组最后一个。
解决问题的时候,经常会遇到图片信息,学生可能会感觉比较棘手,这个时候教师要引导学生善于转化,将图片信息转化成文字信息。根据学生的情况,将具体的图形转化为抽象的数字,符合学生思维发展的顺序,增强了学生学习的动力。
二、转数为形
1. 依托数,解决图形问题
解决实际问题过程中,往往信息比较多,需要学生进行加工整理。而二年级的学生对于信息的整理能力还比较弱,因此需要借助图形进行展示,将题意用线段图的方式表示。因此教师要对线段图进行渗透,帮助学生学会画线段图并理解线段图的含义。
案例3 “解决问题”教学片段
甲:“我们一共要烤90个面包,已经烤了36个。”
乙:“每次能烤9个。”
提问:剩下的要烤几次?
师:仔细读题,你知道了什么?谁能完整地说说这道题的意思?你打算用什么方式解决?
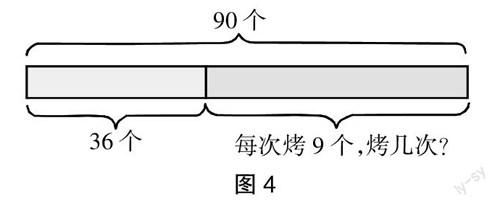
生:可以画图(如图4)。
师:你看得懂这个图吗?蓝色部分表示什么?粉色部分表示什么?
师:你能列式计算吗?
在混合运算解决问题中,信息较多,学生不会进行整理,可以引导学生将获得的信息进行整理分析,转化成图形,有利于学生解决问题。用线段图帮助学生厘清解题思路,引发学生的联想,促进学生形象思维和抽象思维之间的联系,让学生迅速分析问题和解决问题。
2. 依托数,解决实际问题
面对复杂的问题时,数据信息较难分析。比如,在有余数的除法解决问题中,对于余数的取舍难以把握,这个时候通过画图的方式可以清晰明了地表示出题意,帮助判断余数的取舍。
案例4 “有余数的除法解决问题”教学片段
(1)沟通方法,数形结合
例题:22个学生去划船,每条船最多坐4人。他们至少要租多少条船?
在反馈学生的方法(如图5)时,笔者把教学分为两个层次:第一,一个一个地理解方法表示的含义;第二,联系三种方法,将算式中的各个数字画一画、写一写、找一找,帮助学生理解三种方法的本质是一样的,表示的意义也是一样的。在教学中沟通三种方法间的联系,渗透数形结合思想。
(2)练习巩固,扎实基础
二年级的学生较容易受图画影响,所以笔者对选一选中的练习增加了图片,如图6、图7,不仅吸引了学生的注意力,同时也能帮助学生理解对余数的取舍。通过图片,学生更能理解为什么多余的数量要舍去或者进一,进一步巩固本节课的知识,加深对新知的理解。在课外练习中,笔者渗透了数形结合的思想,帮助学生加以巩固。
数形结合思想就是将抽象的数学语言与直观的图形结合起来,使抽象思维与形象思维相结合。因此课堂中,利用数形结合思想解决问题更方便,也更有实效。
总之,教师遵循一定的教育、教学规律,及时根据学生的情况,调整自己的教学预设。当学生学有余力时,适时渗透数形结合思想,丰富方法的多样性,发展学生的思维[2]。学生在解决问题时,具象思维转成抽象思维容易,而抽象思维转成具象思维有难度,故而需要教师加以引导、帮助。因此教师在日常教学中,无论是图形转化成数,还是根据数或式转化成图形,都需要加以重视。数学学习是一个长远的过程,教师需要潜移默化地影响学生,培养学生的思维能力。
参考文献:
[1] 王舒瑶. 数形结合思想在小学数学教学中的应用研究[D]. 西南大学,2015.
[2] 姚建法. 关注数学教材内容的有效解读[J]. 教学与管理,2019(02):30-32.
