网约车新政下平台和乘客的Stackelberg博弈模型及策略研究

雷丽彩, 高 尚

(1.湘潭大学 商学院,湖南 湘潭 411105; 2.南京大学 工程管理学院,江苏 南京 210093)

0 引言

近年来，随着共享经济的迅速崛起，网络约租车(以下简称“网约车”)也应运而生并快速发展。作为互联网企业探索服务行业O2O的先行领域，网约车从出现伊始，在深刻影响城市整体交通状况和城市居民出行方式[1,2]，并在全世界各地都引发了广泛的关注、争议和冲突。在新政正式实施以及垄断巨头酝酿诞生的背景下，多家网约车平台一方面对司机端由“补贴模式”转换为“抽成模式”，使得不少司机选择退出，影响了网约车的市场供应量；另一方面对乘客端悄然降补贴提车价，乘客出行面临“打车难”和出行成本上涨的双重压力，乘客对网约车平台的使用意愿将如何变化？因此，我国网约车平台应该如何制定合理的补贴和抽成策略，从而使得此前一直野蛮生长的网约车市场，在最终进入规范化时代之后，逐渐回归理性化发展，成为交通系统规划与经济管理领域的热点问题之一。

网约车从兴起之初，就受到了媒体和社会大众的广泛关注和争议，也是学者们讨论的热点问题之一。一方面，国内外已有不少关于居民网约车出行行为的研究[3,4]，探究网约车服务使用意愿、消费群体特征以及不同出行服务的对比分析等，从而为制定合理的城市交通规划政策提供对策和建议；另一方面，也有学者探讨了网约车出行方式对城市交通的影响[5,6]，Watanabe等[7]认为，网约车是出租汽车行业的“颠覆性创新”，其影响不亚于一次革命。同时也有不少学者综合运用定量分析和模型仿真的方法来探讨网约车市场主体决策的问题[8,9]，如崔航等[10]构建城镇居民出行需求的系统动力学模型，对居民出行需求的变化进行仿真模拟，提出网约车丰富了城镇居民的出行方式并使居民出行的消费理念发生改变。杨浩雄等[11]在调研乘客个体属性、行为特征的基础上，从复杂系统视角揭示乘客群体行为的动力机制，利用系统仿真模拟乘客出行决策。Lei等[12]基于演化博弈理论构建了网约车出行平台、司机和乘客的三方演化博弈模型，并对其博弈行为演化过程及演化稳定策略进行探讨，以此研究网约车出行市场规制策略的问题。

从研究成果来看，国内外学者对网约车市场的相关研究已有一定的突破，虽然定量仿真模型的采用尚处于起步阶段，但采用模型化研究方法已经逐渐成为发展趋势。在新政实施和行业垄断巨头酝酿诞生的背景下，网约车平台将如何制定乘客端补贴和司机端抽成策略以实现利益最大化，在此政策下而乘客又应如何选择其最优出行方式是本文要解决的主要问题。基于此，本文构建了网约车平台与乘客的Stackelberg博弈模型，并通过相应的数学推导分析，分析了网约车平台的补贴和抽成策略对乘客是否选择网约车出行的决策行为以及网约车市场均衡的影响，为网约车平台的良好健康运营提供实际参考意义。

1 模型说明

1.1 问题描述

随着新政出台和垄断巨头酝酿诞生，一方面，网约车平台不再对乘客端进行高额补贴，需要制定合理的乘客端补贴策略来抢夺市场份额；另一方面，网约车平台对司机端由“补贴模式”转换为“抽成模式”，而抽成策略会直接影响网约车的市场供应量，因此，网约车平台需要根据网约车市场需求量同时制定合理的司机端抽成策略，从而使得我国网约车市场的供需关系达到稳定和平衡。乘客则需根据网约车市场供应量以及平台的补贴力度选择是否乘坐网约车出行。网约车平台与乘客之间存在关于价格(补贴)的先后博弈，属于动态博弈模型中的先行定价模型，因此可将其视为Stackelberg博弈。

1.2 符号说明

D(w)表示出行市场的总需求，其中w表示市场经济状况。R表示网约车平台对乘客端的补贴力度，补贴形式包括打折、红包、返券、充返政策等。C表示网约车平台运营的固定成本支出，包括平台正常运营所需要的人、财、物投入以及平台宣传推广费用投入等。S为网约车的市场供应量，可以用市场上合法运营的网约车车辆数或者网约车司机数量来表示。q表示乘客对网约车的需求量。h表示订单完成后网约车平台对司机端收取的抽成，按照乘客支付金额的百分比进行抽成，相当于传统出租车交的份子钱。p表示平台制定的网约车价格。x表示乘客乘坐网约车的期望价格或支付意愿(Willingness-to-pay,即乘客愿意为乘坐网约车所付出的最高价格)，g(x)和G(x)为期望价格的概率密度函数和分布函数。

1.3 假设说明

(1)根据目前我国网约车市场的现状，本文假设第i个乘客所支付的实际价格pi与所行驶的实际里程si成正比，a为起步价格，b为超过起步里程s0之后的单价。为简化分析，忽略乘客的异质性，假设所有乘客的出行需求都是同质化的[13,14]，因此将乘客乘坐网约车的价格取平均值p，乘客行驶里程取平均值s，以平均价格代替每一个乘客的实际价格，可以得到:

(2)假设乘客乘坐网约车的期望效用U(q)关于需求量q为增函数且二阶可微，边际期望效用关于网约车市场需求量q单调递减，另U(q)=αwln(1+βq)，其中，α和β均为大于零的常数。

(3)假设乘客的期望价格x服从正态分布，g(x)为期望价格的概率密度函数，期望价格的均值和标准差为ux和σx。同时假定某一地区市场上乘客的期望价格x是无差异的，不考虑乘客的异质性所引起的期望价格x的变化。

(4)市场中网约车供应量s与网约车平台对司机端的抽成比例h呈负相关关系，假设网约车市场供应量s是关于网约车平台抽成率h的线性函数，即供应量S(h)=m(1-h/h0)，其中m和h0均为大于零的常数，m表示当抽成率h为0时网约车供应量，h0表示网约车供应量为0时的抽成率，此时网约车司机没有利润可图。

2 Stackelberg博弈模型的构建

在网约车平台与乘客的Stackelberg博弈模型中，网约车平台为领导者(leader)，乘客是后行动一方，为追随者(follower)，网约车平台与乘客双方的博弈时间顺序如下：①作为博弈领导者的网约车平台首先根据其以往的经验以及市场信息，推断乘客的最优出行行为(是否乘坐网约车出行)，确定合理的乘客端补贴R和司机端抽成率h；②作为追随者的乘客观察到网约车平台的定价策略(R,h)，确定网约车市场供应量S(h)，根据其对市场的期望收益函数以及期望价格，确定最优出行决策。③网约车平台支付其固定成本C，获得其收益。

基于Tversky等[15]提出的参考点依赖理论(Reference-Dependent Theory)，乘客在决定是否乘坐网约车出行的决策过程中同样存在参考点依赖的现象，即以其他出行方式作为出行决策的参考点，将乘坐网约车所带来的实际价值与其他出行方式的净收益进行对比来综合判断：令乘客选择其他出行方式所获得的净收益为零，此时，如果乘客选择乘坐网约车出行所获得的收益大于0，则乘客选择网约车服务，否则选择其他方式出行，则乘客的收益函数为:

π1(q)=max{U(q)-(p-R)q,0}

(1)

其中式(1)中的第一项表示乘坐网约车所获得的净收益，第二项表示选择其他出行方式作为参考点所获得的收益为零。

网约车平台的利润函数:

π2(R,h)=hpq-Rq-C

(2)

其中式(2)第一项表示网约车平台通过向司机端抽成所得到的收益；第二项表示网约车平台给乘客端的补贴成本；第三项表示平台投入的固定成本。

3 Stackelberg博弈的分析

本文利用动态规划中的逆向归纳法来求解上述Stackelberg博弈，首先求解作为追随者的乘客的最优决策行为，然后将其代入进一步求解领导者网约车平台的最优补贴策略以及抽成力度(R,h)。

3.1 乘客的最优决策问题

乘客的决策目标是使其期望收益最大化，即可表述为下述的优化问题：

maxEπ1(q)
s.t.O≤q≤S(h)

(3)

对于规划(3)，利用KKT定理(Kuhn-Tucker theorem)求解最优值[16]，得到乘客对网约车的市场需求量最优值q*，满足定理1所述条件。

定理1在网约车市场网约车供应量的约束条件下，网约车乘客的最优需求量为:

(4)

3.2 网约车平台的最优补贴策略和抽成力度问题

在网约车、巡游出租车以及其他交通出行方式共存的交通运输市场，网约车平台决策的难题在于如何实施合理的补贴策略和抽成力度，从而使其自身的期望利润最大化，建立如下规划问题:

maxEπ2(R,h)
s.t.R≥0,h≥0

(5)

对于规划问题(5)，可以得到:

Eπ2(R,h)=E(hpq-Rq-C)=hpEq-REq-C

(6)

根据式(4)，式(6)可以等价为下式(7):

(7)

利用KKT定理求解规划问题(5)的最优解，可以得到网约车平台对乘客端的最优补贴力度R*和司机端的最优抽成力度h*，满足定理2所述条件。

定理2在网约车市场下，网约车平台对乘客端的最优补贴力度以及司机端的最优抽成力度满足如下的方程组:

hpS(h)g(p-R)-S(h)[1-φ(zp-R)]-RS(h)g(p-R)+l1=0

(8)

[hp·∂S(h)/∂h+pS(h)-R·∂S(h)/∂h]·[1-φ(zp-R)]+l2=0

(9)

l1R=0,l2h*=0

(10)

l1≥0,l2≥0,R*≥0,h*≥0

(11)

定理2包含了以下四种可能的情况：①当l1>0,l2>0，可以得到R*=0,h*=0，这种情况只是理论上的最优解,不符合实际情况。②当l1>0，l2=0可以得到R*=0，h*>0,此时平台不采取乘客端补贴策略，并通过采取适当的司机端抽成策略获得利润。③当l1=0，l2>0可以得到R*>0，h*=0,此时平台采取适当的乘客端补贴策略，而不采取司机端抽成策略，这种情况只可能出现在网约车市场发展初期，平台为了扩大市场而采取的策略。④当l1=0,l2=0，可以得到R*>0，h*>0,此时平台同时采取适当的乘客端补贴策略和司机端抽成策略。从网约车平台的运营管理角度来看，定理2表明，在价格优势不再明显的当下，网约车平台运营者应该实施合理的乘客端补贴和司机端抽成策略，同时提供更高效且有品质、有差异化的服务，用服务和品质赢得客户才是网约车市场未来的出路。

4 数值仿真

网约车平台和乘客的Stackelberg博弈模型中相关参数初始设置如下：w=5000，m=2000，h0=0.5，α=20，β=0.05，p=40，μx=40，σx=5，C=15。对乘客乘坐网约车的最优需求量以及网约车平台的最优乘客端补贴策略和司机端抽成策略进行如下的模拟仿真：首先分析乘客的网约车期望需求量Eq和期望收益Eπ1分别与网约车平台的补贴力度R和抽成力度h的演化关系；在此基础上，分析网约车平台的期望利润Eπ2分别与其补贴力度R以及抽成力度h的演化关系。

4.1 乘客最优决策的算例分析

4.1.1 乘客的网约车期望需求量与平台补贴力度和抽成力度的演化关系

乘客是否乘坐网约车出行的决策行为主要与网约车平台的乘客端补贴力度(影响乘客乘坐网约车出行的成本)和司机端抽成力度(影响网约车的市场供应量)有关。首先由图1(a)可以看出乘客对网约车市场的期望需求量与平台对乘客端的补贴力度呈正相关关系，与平台对司机端的抽成力度呈负相关关系。图1(b)直观地反映了不同的抽成力度下，乘客端补贴力度对网约车市场期望需求量的影响程度是不同的，但随着平台对乘客端的补贴力度增加，期望需求量经过初始的平缓增长后逐渐稳定在某一个值，即网约车的市场供应量，由此定理1的结论得到验证。这是因为在补贴力度增加到乘客选择网约车的出行成本等于其支付意愿时，补贴政策在一定程度上弥补了因网约车供应量减少而造成的用户体验差的负面效应。

图1(c)反映了在不同的补贴力度下，随着平台对司机端的抽成力度的增加，乘客对网约车市场的期望需求量逐渐递减，这是因为平台对司机端抽成力度过大，网约车司机到手的收入减少使得大量司机退车离场，从而网约车平台可提供的车辆供应量减少，使得乘客打车难，或者在线下单后没有司机及时应答抢单，乘客满意度降低导致其对网约车的市场需求量减少。

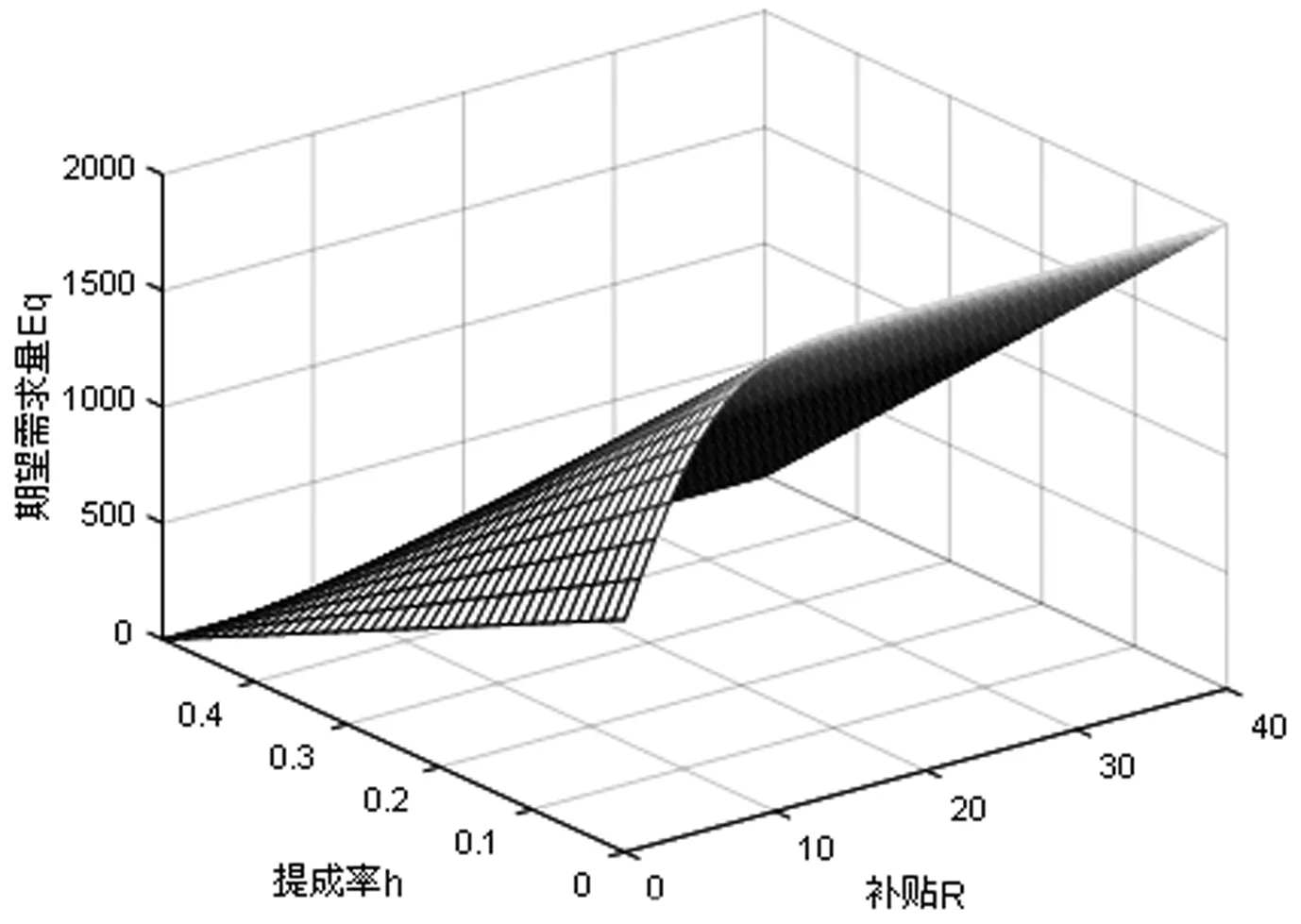
(a)期望需求量与平台补贴力度和抽成力度的演变关系

4.1.2 乘客期望收益与平台补贴力度和抽成力度的演化关系

由上一节的结论可知，随着网约车平台对乘客端补贴的增加和司机端抽成比例的减少，乘客对网约车市场的期望需求量逐渐增加，而乘客的期望收益与其对网约车市场的期望需求量呈正相关关系，图2(a)关于乘客的期望收益与网约车平台的补贴力度R和抽成力度h的演化关系图正好验证了这一结论。

(a)期望收益与平台补贴力度和抽成力度的演化关系

同理，从图2(b)可以看出，在网约车平台不同的抽成力度下，乘客的期望收益随着平台对乘客端补贴力度的加大而逐渐递增，但是当网约车平台抽成力度达到某个值时，乘客的期望收益随抽成比例递增的幅度逐渐变小，这是由于当网约车平台的抽成力度较大时，不断流失的司机资源使得网约车的市场供应量减少，平台补贴所带来的期望需求量的增加幅度非常有限。

从图2(c)可以看出在网约车平台不同的补贴策略下，乘客期望收益随着平台对司机端抽成力度的加大而逐渐递减，这是因为当网约车平台对司机端抽成力度较大时，网约车的市场供应量减少，不能及时满足乘客随时随地出行的需求，因此乘客的期望收益下降。

4.2 网约车平台的最优乘客端补贴策略和司机端抽成策略的算例分析

下面对网约车平台为了达到其期望利润最大化目标而采取的最优乘客端补贴策略和司机端抽成策略进行模拟仿真。图3(a)反映了网约车平台的期望利润与其对乘客端补贴R和司机端抽成h的演化关系(当补贴力度较大而抽成力度较小时，网约车平台的期望利润为负值，此时的演化结果图3没有呈现出来),当平台补贴力度为R=6，且抽成力度为h=0.325时，网约车平台的期望利润达到最大值，由此验证了定理2。

从图3(b)可以看出，当网约车平台的司机端抽成力度较小时，其期望利润随着乘客端的补贴力度增加而不断减小，这是因为平台所承担的补贴费用的增幅高于其所获得的抽成收入增幅。当司机端抽成力度较大时，网约车平台的期望利润随乘客端补贴力度的增加呈现先递增后递减的变化趋势，这是因为对乘客端的适度补贴策略可以在一定程度上刺激消费者的消费欲望，使网约车平台的期望利润递增，但是乘客端补贴力度一旦超过某临界值，平台需支付的补贴费用的增幅超过其所获得的抽成收入的增幅，网约车平台的期望利润开始不断下降。

从图3(c)可以看出，在不同的补贴力度下，网约车平台的期望利润随着抽成力度的增加呈现先递增后递减的变化趋势，这是因为在一定的抽成力度下，网约车平台从司机端获得的抽成收入增加，使得其期望利润不断增加，但是当抽成力度超过某临界值时，不断流失的司机资源使得网约车市场供应量不足，导致网约车平台的期望利润逐渐下降。

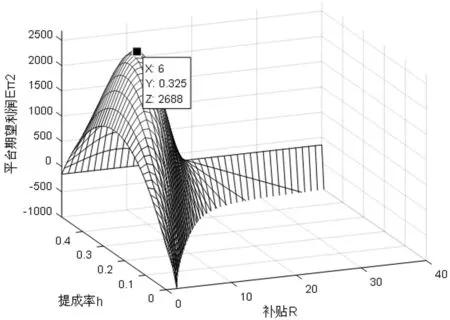
(a)期望利润与其补贴力度和抽成力度的演化关系

5 结论

网约车逐渐成为城市居民出行不可或缺的交通方式，此前“烧钱补贴”一直是网约车企业拓展市场的重要方式，自滴滴出行和中国优步合并、2016年11月1日网约车新政正式落地以来，网约车市场已经从烧钱扩展模式转变为策略竞争模式市场。但多家网约车平台开始对乘客端降补贴提车价，同时对司机端采取高额抽成，这在一定程度上降低了乘客对网约车的使用意愿，打击司机加入网约车市场的积极性。

因此，本文通过构建网约车平台和乘客之间的Stackelberg博弈模型，分析网约车平台的最优补贴和抽成策略以及乘客的最优出行决策，通过模型求解和算例分析，得到如下主要结论：网约车平台的期望利润与司机端抽成力度的变化关系呈现为“倒U型”曲线，即司机端抽成力度较低时，网约车平台的期望利润呈现正常的上升趋势，但是当抽成力度增加到一定值，网约车的市场供应量达到一定的临界值(高点)时，网约车平台的利润会出现停滞不前甚至严重的利润下降趋势；此外，随着网约车平台对司机端的抽成策略不同，网约车平台的期望利润与乘客端补贴力度呈现不同的演化趋势，也就是当网约车平台的抽成力度较小时，其期望利润随补贴力度增加而单调递减；但是当网约车平台的抽成力度较大时，其期望利润随补贴力度的增加呈现先递增后递减的变化趋势，即此时网约车平台的利润为补贴力度的“倒U型”曲线。

本文的研究有利于网约车平台制定更加合理恰当的乘客端补贴和司机端抽成策略，控制市场网约车供应量，降低网约车车辆供给“供过于求”或“供不应求”以及网约车平台补贴成本过高“烧钱补贴”的风险，实现网约车平台的利润最大化，提高其核心竞争力，进而实现社会的帕累托改进。