考虑患者止步行为的动态入院接收决策模型

姜艳萍, 杨飞飞, 孙 灿

(1.东北大学 工商管理学院,辽宁 沈阳 110167; 2.北京工业大学 经济与管理学院,北京 100124)

0 引言

如何合理高效的利用有限的病床，为患者提供高质量医疗服务水平，已经成为备受医患关注的社会问题[1,2]。在大型公立医院的运营管理中，患者的入院接收决策一直是一项必不可少的日常工作，且病床作为医疗资源的关键之一，极大地影响着整个医院的运作效率和整体服务水平[3]。目前，在供需矛盾突出的医院，当病房没有合适的病床时，等待住院的患者在提出住院请求后往往需要在家等待几天甚至几个月，直到医院打电话通知患者住院[4,5]。由于对疾病和等待的敏感度和心理承受度不同，一些患者在收到等待通知时往往发生止步行为。所谓止步行为是指当预期住院等待时间超出患者可忍耐限度时，患者放弃当前医院住院申请而转向其它医院就诊的行为。止步行为的发生会降低患者满意度，等待时间随着患者患病严重程度和就诊科室的不同而不同，并且该行为会引发患者对医院资源分配不公平不合理的抱怨，从而导致医患矛盾增加、科室拥堵和医院整体服务效率低下等问题。因此，医院在入院决策中如何考虑患者止步行为，制定合理有效的患者入院接收决策是一个值得研究的问题。

针对患者入院接收决策问题研究近年来逐渐得到学者的关注，学者采用不同的方法进行研究，以得到合理的入院策略[6,7]。Huh等[8]研究动态非平稳环境下择期患者与急诊患者的多资源分配问题，其中患者会发生中途离开行为。Samiedaluie等[9]研究了神经科患者的住院策略，建立了无限维平均成本动态规划，并提出一种有效的近似动态规划解决大规模问题实例。目前，虽然关于顾客止步行为的服务系统问题已经展开了一些研究[10,11]，但已有文献考虑患者止步行为的动态入院接收决策文献仍然较少。部分文献用实证方法分析了患者止步行为给医院带来的影响。Kremer和Debo[12]研究并观察消费者等待时间和行为的影响。Osadchiy等[13]运用实证方法探索了患者止步行为和患者爽约之间的相互关系。部分文献利用仿真方法或排队理论定量的分析了患者止步行为下系统性能。LeBlanc等[14]用仿真的方法研究了考虑患者止步行为的急诊部门入院控制问题。Lu等[4]为减少患者盲目等待与无用等待，提出了一种基于等待依赖的最优动态预约调度形式化框架，以最大限度平衡待入院患者的服务效用和体验。Zacharias和Armony[15]考虑了患者止步行为和中途离开行为，研究了确定每天能力和提供预约时段数量的联合优化问题。

需要指出的是，已有研究提供了患者入院接收决策问题的背景依据以及决策方法，部分文献在入院接收决策研究中考虑了患者的策略性行为[12,13]，但没有考虑患者止步行为对随机入院优化系统的影响。文献[4,5,14,15]研究患者策略性行为的入院调度问题，但大多集中刻画患者止步行为下系统的性能，缺少患者住院背景下由于医院响应速度、服务主动性以及资源分配公平性等因素导致的患者止步行为。鉴于此，本文针对患者动态入院接收决策问题，构建无限时域总折扣报酬马尔可夫决策过程(MDP)。与以往文献相比，该模型基于患者随机到达和住院时长不确定的特征下，考虑具有等待空间下的患者入院决策问题。进一步地，该模型重点考虑了患者在等待过程中发生的止步行为。本文以使医院的期望收益最大作为决策目标，建立无限时域连续时间马尔可夫决策模型，通过模型求解得到最优患者入院策略。

1 问题描述

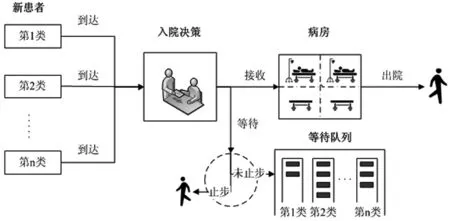
图1 考虑止步行为情形下患者到达时的入院接收决策

当已住院患者接受完治疗出院时，医院根据新患者到达信息、病床可用性和等待队列信息做出相应决策：令等待队列中某位患者进入病房？还是不采取行动？科室若决定令等待队列中某位患者进入病房，则该患者开始住院接受治疗，等待队列中相应类别患者数量减少，病房内相应类别患者增加；若决定不采取行动，则等待队列与病房内患者数量不发生变化。

2 模型假设与符号设定

在考虑患者止步行为的入院接收决策问题中，给出如下假设：1)假设该科室的总床位数固定，且所有病床具有通用性。2)假设等待队列中的患者不会中途离开。3)假设患者的到达过程与服务过程相互独立，患者的到达过程服从泊松分布，且同类患者服从参数相同的分布；患者的住院时长服从负指数分布，且同类患者服从参数相同的分布。

符号说明：

B：单科室病房内总床位数量；

n：患者类型总数量；

i：患者类型，i=1,2,…,n；

wi：当前时刻第i类患者等待数量，即第i类患者等待队列长度；

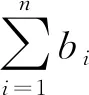
λi：第i类患者到达率，即单位时间内第i类患者到达数量；

μi：第i类患者服务率，即单位时间内第i类患者服务数量；

ri：科室服务一个第i类患者的收益，服务患者收益向量为r=(r1,r2,…,rn)；

πi：第i类患者单位时间等待成本，患者等待成本向量为π=(π1,π2,…,πn)；

li：一位第i类患者出现止步行为后对科室造成的损失；

αi：第i类患者止步率；

pi：第i类患者止步行为发生概率；

ci：决策变量，ci∈{0,1}，表示当前时刻科室是否令第i类患者进入病房，ci=1代表令患者进入病房，ci=0代表令患者加入等待队列；

dij：决策变量，dij∈{0,1}，j=1,2,…,n，dij=1表示病房内一位第i类患者出院时，令等待队列中一位第j类患者进入病房，dij=0表示不做决策。

3 考虑患者止步行为的入院接收决策MDP模型构建

3.1 止步行为概率函数

当科室做出让患者加入等待队列决策后，患者往往通过询问知晓队列长度，并根据队列长度和医院服务时间判断出预期等待时间。此外，不同类型患者的不耐烦程度不同。因此患者止步行为的影响因素包括等待队列长度及患者不耐烦程度。患者相应等待队列长度wi(i=1,2,…,n)越大，患者止步行为发生概率越高。本文用αi代表第i类患者的止步率，其中αi∈[0.1,0.9][4]。止步率反映了不同类型患者的不耐烦程度，在其他条件相同情况下，患者止步率越大，患者止步行为发生概率越高。本文参考文献[1]中止步函数，则新到达第i类患者发生止步行为的概率为pi=1-eαi·wi。

3.2 马尔可夫决策模型

由于患者住院具有到达随机并且住院时长不确定的特征，为了确定考虑患者止步行为动态入院接收问题的最优决策，本文建立无限时域连续时间折扣型马尔可夫决策过程。下面详细介绍MDP模型构建过程。

(1)状态。科室需要统计等待队列中患者人数以及病房内已住院各类患者人数，故定义系统状态空间集合为

Ω={(w,b)|w=(w1,w2,…,wn)T,

(1)

(2)行动。当新患者到达和已住院患者出院，科室会做出以下行动：

①当某个第i类患者随机到达时，科室决定令该患者直接进入病房或者加入相应等待队列。因此，第i类患者到达时的行动集可表示为:

(2)

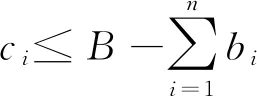
②当病房内某个第i类患者服务完成出院时，科室决定让等待队列中一位第j类患者进入病房或者不采取行动。因此，病房内第i类患者出院时的行动集可表示为:

Di(w,b)={(di1,di2,…,din)∈{0,1}n|dij∈wj,

(3)

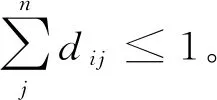
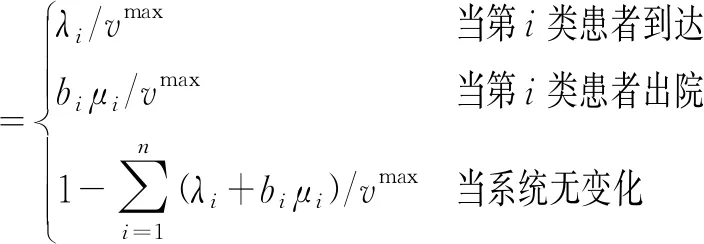
(4)

(4)贝尔曼方程。令Vt(w,b)表示从当前时刻t状态(w,b)开始，到计划期末尾的期望总收益。对于∀i∈{1,2,…,n},∀(w,b)∈Ω

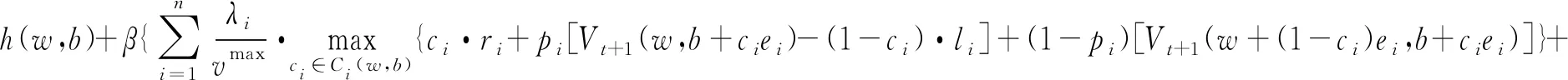
(5)

其中h(w,b)=-π·w，表示当前时段患者总等待成本；β为时间折扣因子；ei是n维单位列向量，它的第i行元素为1，其余元素均为0。为了更清晰的理解贝尔曼方程，我们对式(5)相应状态变化做进一步分析如下：

(1)当系统中新到达一个第i类患者时，科室要从以下两个行动中挑选使期望收益最大化的行动：其一令该患者直接进入病房，即ci=1，此时ri+Vt+1(w,b+ei)；其二是令新患者加入等待队列，即ci=0，此时pi[Vt+1(w,b)-li]+(1-pi)[Vt+1(w+ei,b)]，该行动下该患者将以一定概率发生止步行为。

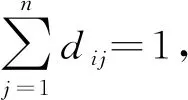
(3)当系统中既无患者到达又无患者出院时，科室无需进行决策，状态不发生变化。

4 模型分析和求解算法

下面，对值函数进行结构性质分析，从而确定最优策略。值得注意的是，由于值函数具有多维状态空间，多维函数下的值函数性质及最优策略较为复杂。

定理1对于i=1,2,…,n，若f(w,b)是分量凹(component-wise concave)函数[17]，则V(w,b)是分量凹函数。

证明首先，为了便于分析，定义到达算子和离去算子分别为

TAif(w,b)=max{ri+f(w,b+ei),

pi[f(w,b)-li]+(1-pi)f(w+ei,b)}

(6)

TDif(w,b)=max{r1+f(w-e1,b-ei+e1),…,rn+

f(w-en,b-ei+en),f(w,b-ei)}

(7)

则式(5)可以重写为

V(w,b)=Tf(w,b)

(8)

为了证明V(w,b)是关于每一维自变量都是凹的，我们需要分别证明TAif(w,b)和TDif(w,b)是关于分量元素的凹函数。下面，以i=1为例，给TA1f(w,b)出的详细证明过程，TDif(w,b)的证明类似，在这里我们省略证明过程。

假设f(w,b)是关于w分量元素的凹函数，则

TA1f(w+ei,b)-TA1f(w,b)-(TA1f(w,b)-TA1f(w-ei,b))

=max{r1+f(w+ei,b+e1),p1[f(w+ei,b)-l1]+(1-p1)f(w+e1+ei,b)}-

2max{r1+f(w,b+e1),p1[f(w,b)-l1]+(1-p1)f(w+e1,b)}+

max{r1+f(w-ei,b+e1),p1[f(w-ei,b)-l1]+(1-p1)f(w+e1-ei,b)}

由于max{A,B}=max{A-B,0}+B和max{A,0}-max{B,0}≤max{A-B,0}，并且f(w,b)对每一维自变量都是凹的，可知

TA1f(w+ei,b)-TA1f(w,b)-(TA1f(w,b)-TA1f(w-ei,b))

≤max{f(w+ei,b+e1)-f(w,b+e1)-f(w,b+e1)-f(w-ei,b+e1))

-p1[(f(w+ei,b)-f(w,b))-(f(w,b)-f(w-ei,b))]

-(1-p1)[f(w+e1+ei,b)-f(w+e1,b)-(f(w+e1,b)+f(w+e1-ei,b))],0}

+p1[f(w+ei,b)-f(w,b)-f(w,b)+f(w-ei,b)]

+(1-p1)[f(w+e1+ei,b)-f(w+e1,b)-f(w+e1,b)+f(w+e1-ei,b)]≤0

V(w,b)关于b分量元素的凹函数的证明类似，在这里我们省略证明。由此可知，若f(w,b)是分量凹函数，则V(w,b)是分量凹函数。

基于以上分析，下面给出最优动态入院接收策略如下。

(1)当第i类新患者到达，分别比较ri+Vt+1(w,b+ei)和pi[Vt+1(w,b)-li]+(1-pi)[Vt+1(w+ei,b)]，选择使得医院收益最大的行动；

(2)当第i类患者出院，分别比较从等待队列中挑一位j类患者入院(如果队列中存在j类患者)rj+Vt+1(w-ej,b-ei+ej)和不作行动Vt+1(w,b-ei)，选择使得医院收益最大的行动。

下面给出确定最优动态入院接收策略的值迭代算法。

步骤1参数赋值，给定阈值ε=10-3，令迭代次数k=0，初始化V(0)(w,b)=0,∀w,b；

步骤2K=k+1;

步骤3对每个状态(w,b)∈Ω，依据式(5)计算出的值V(k+1)(w,b)；

步骤4若‖V(k+1)(w,b)-V(k)(w,b)‖≤ε，则转到步骤5；否则返回步骤2；

步骤5算法终止，对每个状态(w,b)∈Ω，输出V(k+1)(w,b)，并提取最优策略π(w,b)。

5 数值实验

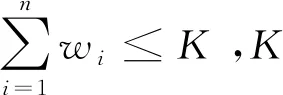
我们研究n=3，K=4,B=3的情景，并且设置其它参数为：λ1=4,λ2=5,λ3=3;μ1=1.1,μ2=1,μ3=1.2;α1=0.1,α2=0.1,α3=0.2;l1=0.2,l2=0.15,l3=0.15;k1=3.5,k2=2.5,k3=0.5;r=(10,8,7.5);π=(0.5,0.4,0.37);β=0.9;迭代阈值ε=0.001。采用Python 3.7编程语言设计值迭代算法进行求解。算法运行环境为CPU：Intel(R) Core(TM) i5-3337U CPU @ 1.80GHz(4 CPUs) 1.8GHz，RAM: 4.00GB，操作系统：Windows 8.1中文版64位。可知，该算例的系统状态总数为700，算法经过62次迭代后停止，我们得到最优动态入院策略。

在每个状态空间(w,b)=(w1,w2,w3,b1,b2,b3)情况下，包含新患者到达时的入院接收决策与病房内患者出院时的入院接收决策。患者到达入院接收决策变量ci可取值0、1、2 (其中ci=2表示拒绝患者)，因此患者到达入院策略(c1,c2,c3)共计33=27种入院策略。其中，适用状态的入院策略有5种：(0,0,2)、(0,2,2)、(1,1,1)、(1,1,2)、(2,2,2)。该5种入院策略及其系统状态数量关系如图2所示。

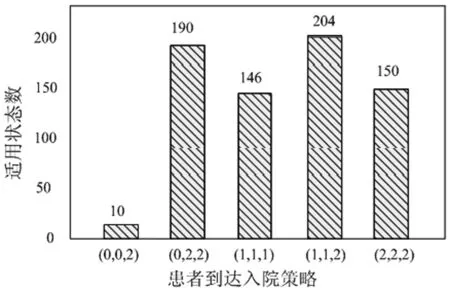
图2 患者到达入院策略及适用状态数

我们对这5个可用患者到达入院策略进行分析整理，得出此案例中针对慢性病情下考虑患者止步行为的入院接收策略：

①当等待队列为空，且有可用空床，即b1+b2+b3<3时，科室令所有类型新到达患者进入病房，即(c1,c2,c3)=(1,1,1)；

②当等待队列为空，且无可用空床，即b1+b2+b3=3时，科室令新到达的第1类与第2类患者加入等待队列，拒绝第3类患者令其转院，即(c1,c2,c3)=(0,0,2)；

③当等待队列非空，即w1+w2+w3>0，且病房内住院患者不超过1个，即b1+b2+b3∈{0,1}时，科室令所有类型新到达患者进入病房，即(c1,c2,c3)=(1,1,1)；

④当等待队列非空，且病房内住院患者为2个，即b1+b2+b3=2时，科室令新到达的第1类与第2类患者进入病房，拒绝第3类患者令其转院，即(c1,c2,c3)=(1,1,2)；

⑤当等待队列非空也未到达上限，即w1+w2+w3∈{1,2,3}，且无可用空床时，科室令新到达的第1类患者加入等待队列，拒绝第2类与第3类患者令其转院，即(c1,c2,c3)=(0,2,2)；

⑥当等待队列到达上限，即w1+w2+w3=4，且无可用空床时，科室拒绝所有类型新到达患者令其转院，即(c1,c2,c3)=(2,2,2)。

患者出院入院接收决策变量di可取值0，1，2，3。其中，di=0表示第i类患者出院时，医院不采取行动，di=1,2,3分别表示第i类患者出院时，令等待队列中的第类患者进入病房。因此患者出院入院策略(d1,d2,d3)共计43=64种情况，图3给出可用入院策略及其适用状态关系图。

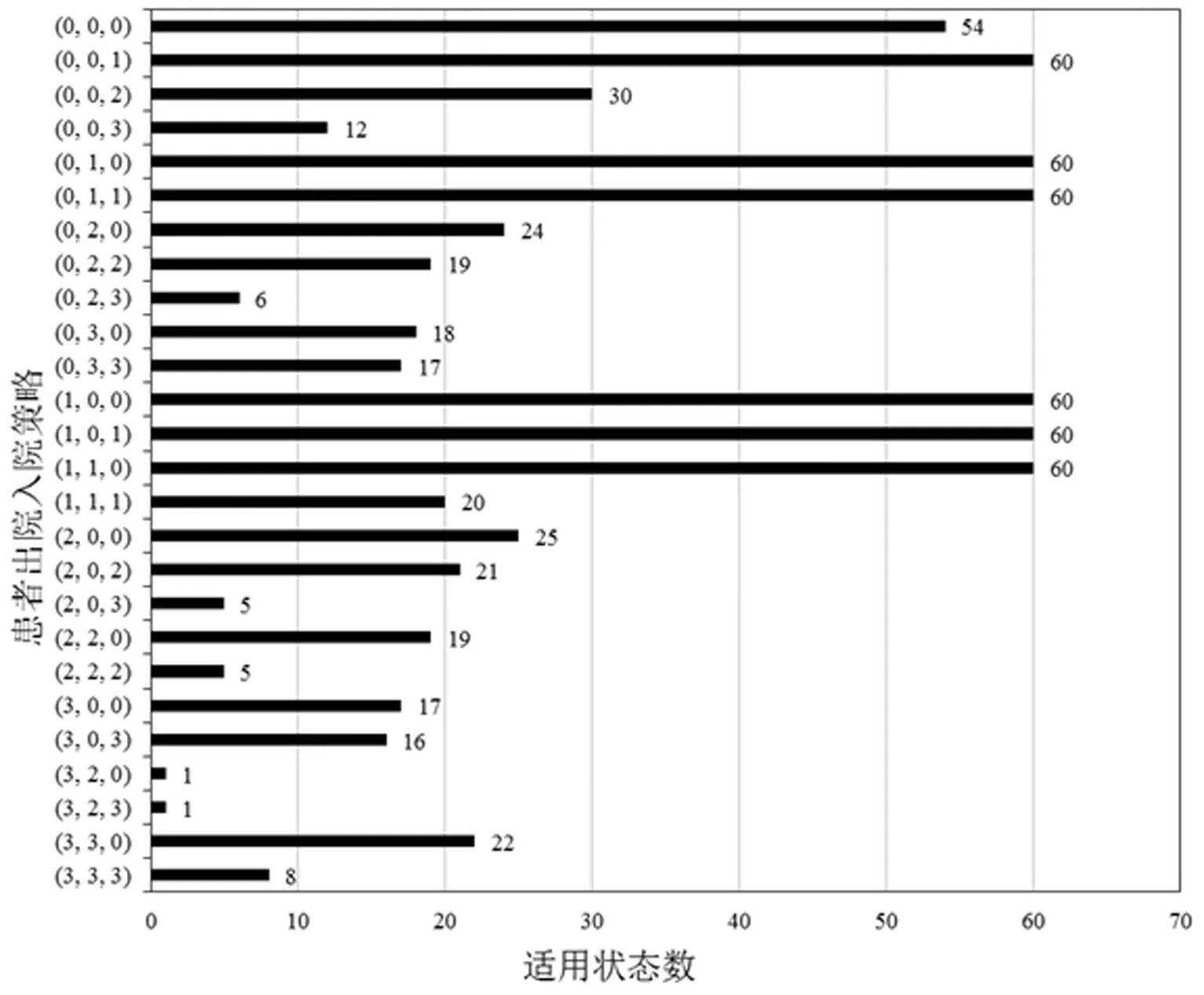
图3 患者出院入院策略及适用状态数

通过对患者出院策略进行分析整理，可知在给定状态下，病床管理者是选择为未来到达的病重患者保留空床，还是选择从等待队列中挑选患者进入病床的行动。当病床管理者选择从等待队列中挑选患者入院时，病情相对严重的患者优先级大于病情较轻的患者，且相同优先级患者服从先到先服务规则。

进一步地，本文使用蒙特卡洛仿真探究本文策略与先到先服务(FCFS)策略的优劣。参数设置与上述算例相同，仿真生成120个事件，共仿真200次。计算期望收益和平均等待队长作为评价指标，分别得到图4和图5结果。图4仿真结果表明，考虑止步行为下的MDP最优策略的期望收益整体比FCFS策略高。图5仿真结果表明，考虑止步行为下的MDP最优策略平均等待队长整体比FCFS策略短。因此，本文提出的考虑止步行为的动态入院接收决策提高了医院总期望收益，缩短了平均等待队长，提高了整个服务系统效率。

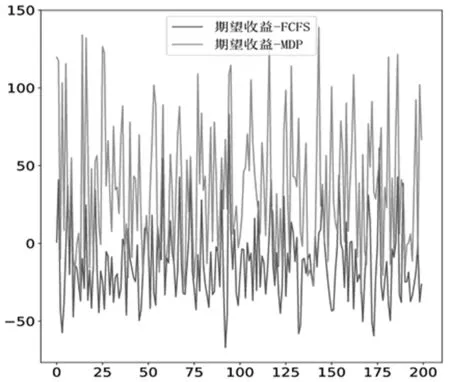
图4 策略对比-期望收益

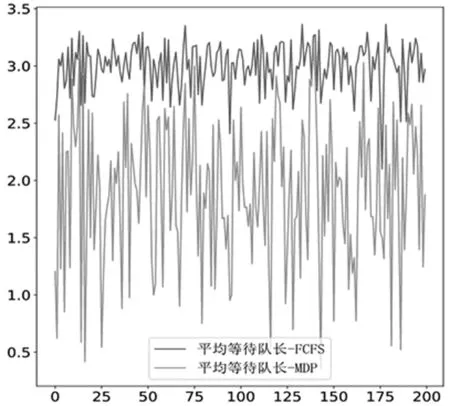
图5 策略对比-平均等待队长

6 结束语

本文基于现实医院住院管理中，一些患者在收到等待通知时往往发生止步行为现象，其患者病情严重程度不同，随机到达和住院时长不确定等特点，构建了考虑患者止步行为入院接收MDP模型，对医院期望收益值函数进行了一些性质分析，证明了值函数对每一维自变量的凹性，进一步给出最优动态入院接收策略及求解算法。实验结果给出了一定情景下的最优动态入院接收策略。与已有患者入院接收决策问题不同的是，本文考虑患者止步行为贴近现实，这样可以合理有效分配病床，缓解医患关系紧张，提高患者满意度和整体运作效率。本文为患者入院接收决策问题提供了理论依据和支撑，为住院决策管理给出了管理建议，对住院部的日常科学管理有一定的建议指导作用。未来的研究中可以加入等待期间患者中途离开行为，并且考虑设计大规模求解算法来克服维度爆炸问题。