需求不确定影响下政府为绿色产品提供补贴的最优策略
2022-10-20海江涛李正义
海江涛, 李 旭, 李正义
(1.河南大学 商学院,河南 开封 475004; 2.复旦大学 管理学院,上海 200433; 3.南京林业大学 经济管理学院,江苏 南京 210037)
0 引言
目前,随着环境恶化、资源匮乏等全球性问题的出现,可持续发展进入了以绿色经济为主驱动力的阶段,绿色技术创新在世界各地兴起。企业推动绿色技术创新具有一个典型特征是“双重外部性”,即在生产过程中具有技术溢出效应,而在消费过程中,还由于改善了环境质量、降低了外部环境成本而产生了环境外部效应[1]。环境外部效应的存在使绿色产品所创造的价值被整个社会占有,进行绿色创新的企业将会比未进行绿色创新企业承受更多的投资压力,这直接导致了消费者因为绿色产品价格高昂而不愿意购买的结果。因此,该如何化解绿色产品消费过程中的环境外部效应就成了政府部门要解决的重要问题。
政府财政补贴作为一种解决正外部性的手段,已经在政府部门工作中得到了较多应用。政府部门为化解环境外部效应带来的不利影响,可以选择为购买绿色产品的消费者提供补贴或者给生产绿色产品企业提供补贴。给消费者提供补贴的方式主要有两种:固定额度补贴与价格折扣。在新能源汽车消费市场上,固定额度补贴在我国是一种常见补贴类型。在2017年,我国政府为续航400km以上纯电动车型提供的补贴是4.4万元/辆。而在罗马尼亚和希腊等国家,政府部门对新能源汽车消费者提供了约25%的价格折扣。政府除了选择给消费者提供补贴之外,还会选择给生产绿色产品企业提供补贴,比如宇通客车于2018年收到郑州市财政局转移支付的国家新能源汽车第二批推广补贴款586,022万元。
部分学者探讨了政府补贴对消费者购买绿色产品的影响。Cohen等[2]分析了需求不确定因素影响下,政府该如何给消费者提供补贴以激励消费者购买绿色产品问题。Lulu Shao等[4]假定企业能够完全了解消费者需求,按照消费需求进行生产,比较了补贴机制与打折机制对消费者购买绿色产品的影响。赵爱武等[5]运用计算实验方法模拟了消费者对绿色产品的购买行为。范如国和冯晓丹[5]研究发现,只有地方政府补贴在小于等于最优配套比例或价格补贴比例上限时,才会对新能源汽车的市场推广产生正向影响。
部分学者探讨了政府补贴对绿色产品生产企业的影响。Luo等[6]以绿色产品生产企业实现产量最大化为目标,分析了价格折扣和补贴上限的影响,比较了两种机制对激励企业生产绿色产品的影响。孙迪和余玉苗[7]构建政府为绿色产品生产企业或消费者提供补贴的博弈模型,分析了两种补贴政策作用下实施效果的差异。罗春林[8]利用合作博弈方法研究了电动汽车供应链上企业的期望销量与最优定价等问题。张海滨等[9]探讨了政府补贴与新能源汽车销售企业努力程度的关系问题,研究了政府补贴力度、获取补贴的销售目标等因素对企业绩效的影响。孙红霞和吕慧荣[10]研究了补贴退坡政策影响下政府和企业的演化稳定策略。
绿色产品的市场需求往往具有随机性。Sallee[11]构建实证模型研究了税收抵免政策对美国部分地区消费者购买新能源汽车的影响,税收抵免政策实施导致了某些车型出现卖断货的情况。Dai等[12]分析了折旧参数、订单单位成本等外生变量对生产企业决策的影响,讨论了报童模型中最优价格和最优产量的存在性问题,研究中他们假定市场需求函数为乘积形式。
政府可以选择给绿色产品供应企业或者购买者提供补贴,这对化解环境外部效应具有积极意义。分析现有研究,需求不确定情况下政府部门该选择给消费者还是给供应企业提供补贴的问题目前还缺乏系统研究。以下将在理论模型基础上,首先分析政府为购买绿色产品消费者提供补贴的情况,然后,分析政府为绿色产品生产企业提供补贴的情形,并对这两种情形进行比较。研究结果对政府部门解决绿色产品消费过程中的环境外部效应问题具有一定的现实意义。
1 基本模型
事件发生顺序如下。首先,政府部门明确补贴政策,选择给购买绿色产品的消费者固定额度补贴r或提供价格折扣k,或者给供应企业提供补贴s,过程如图1所示。两个①用虚线表示的含义是两者选其一。在这之后,供应商决定产品价格和产量,消费者在市场上购买绿色产品,整个过程用一个两阶段斯坦科尔伯格模型进行描述。
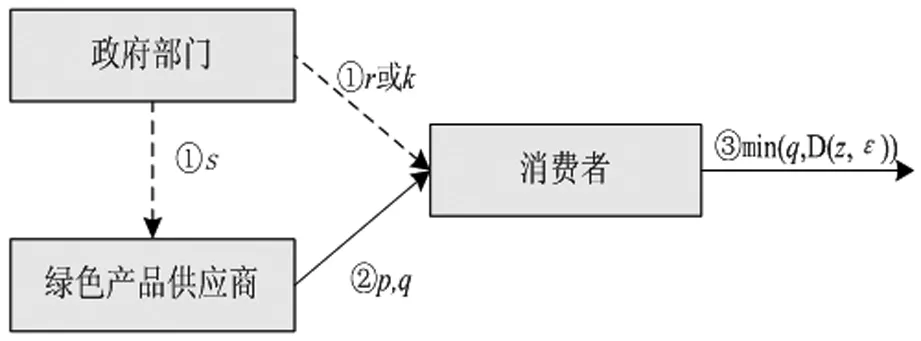
图1 事件发生顺序
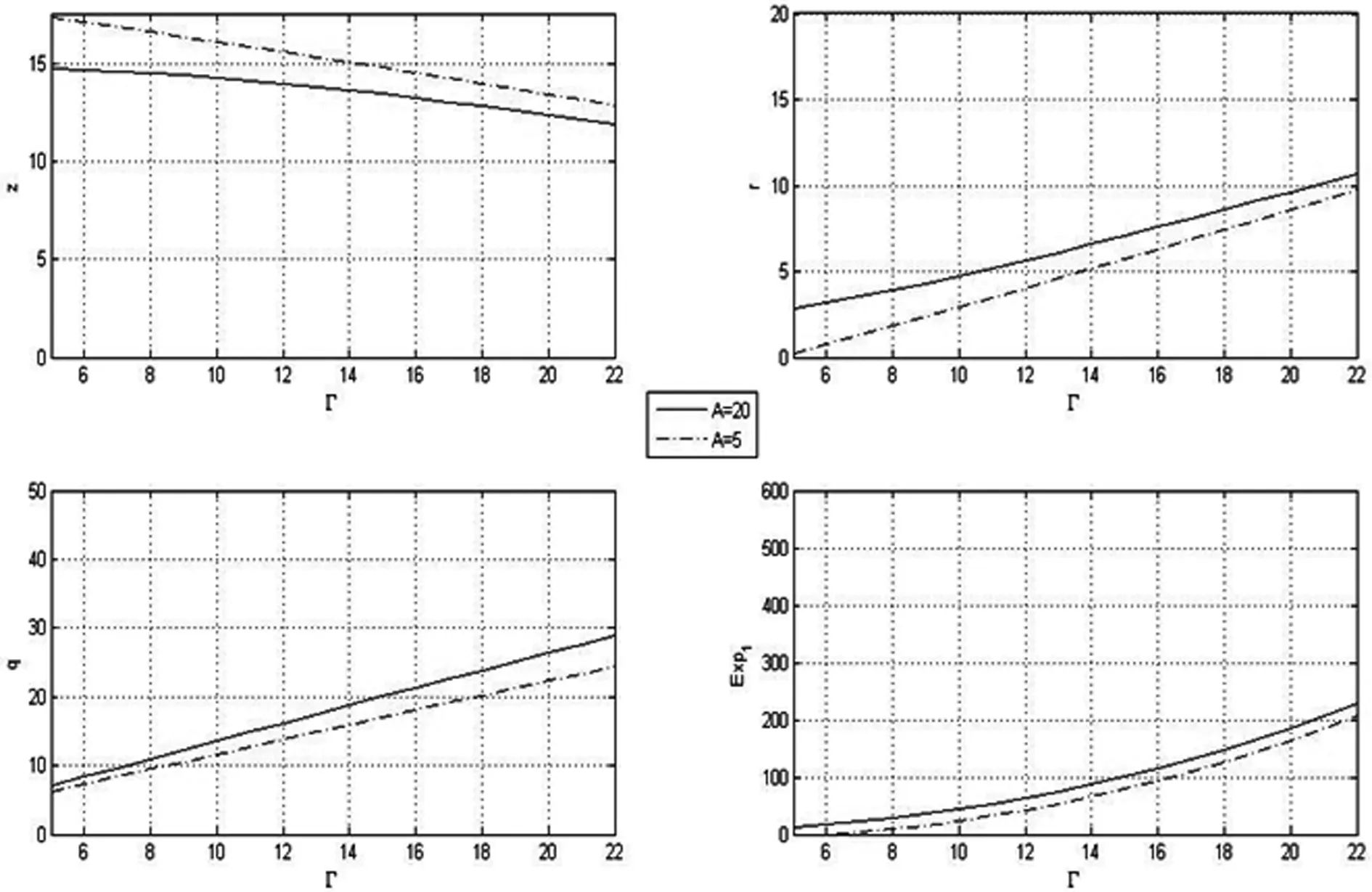
供应商了解到政府补贴政策之后,确定产品价格p以及产量q。政府为消费者提供固定额度补贴时,其实际购买价格为z=p-r。政府给消费者一个价格折扣时,消费者实际购买价格为z=(1-k)·p(0 根据随机需求的报童模型,消费者对绿色产品的需求由z和随机变量ε共同决定,也即是市场对绿色产品的需求为D(z,ε),一旦需求确定,产品的实际销量也确定,即为min(D(z,ε),q)。D(z,ε)可能为加法形式或者乘积形式。D(z,ε)是加法形式情况下,产品实际购买价格影响了需求分布的位置;D(z,ε)为乘积形式时,产品实际购买价格直接影响了需求分布的方差。以下研究中,给定随机变量ε的分布函数为F(·),概率密度函数为f(·)。 假定政府提供补贴以激励绿色产品销量达到预期目标,该目标销量用表示。比如,我国工信部在落实国务院印发的《打赢蓝天保卫战三年行动计划》中明确2020年实现产销量达200万辆新能源汽车的目标。政府希望以最少的财政支出实现上述目标,应用固定额度补贴方式时其目标函数为 pco2·E[min(q,D(z,ε))])} s.t.E[min(q,D(z,ε))]=Γ (1) r≥0 应用价格折扣方式时,政府目标函数为 pco2·E[min(q,D(z,ε))])} s.t.E[min(q,D(z,ε))]=Γ (2) 1>k≥0 政府给供应企业提供补贴时,其目标函数仍然是补贴支出最小化。也即 s.t.E[min(q,D(z,ε))]=Γ (3) s≥0 需要对参数pco2进行解释。消费者在市场上每购买一单位绿色产品,在消费中就能减少一定量CO2的排放,这将给环境带来正外部收益,这种正收益用参数描述。以新能源汽车为例,每一辆电动汽车推向市场之后可以减少约50.3吨CO2排放,而每减少一吨CO2排放则可以为环境带来正收益约23.3$。因此,每一辆电动汽车销售出去之后,可以实现的正收益约为1172$[13]。 企业生产绿色产品之前就清楚政府补贴政策。为分析需求不确定性对消费者购买绿色产品以及政府决策产生的影响,暂不考虑市场上存在多家企业竞争的情形。假定市场上某企业垄断某绿色产品的生产和供应,企业目标函数如下: (4) 参数c为产品边际成本,既包括了产品的单位制造成本也包括了企业提升制造能力所产生的单位成本。 以电动汽车为例,蔚来ES8、威马ex5在进入市场之后,企业自主决定产品零售价格以及生产产量。以下将讨论企业自主定价的情形,首先分析企业如何根据补贴政策确定最优价格和产量,然后再讨论政府最优补贴问题。 2.1.1 政府提供固定额度补贴情形 采用逆向归纳法,首先给定补贴r分析供应企业如何确定p和q问题,然后再讨论政府如何确定最优补贴r。企业的收益函数为 (5) 参数h表示未销售产品的折旧值,以下研究中给定h取值范围为0 (6) 变量u为企业的库存决策,u值大于参数ε时,未销售出去的产品只能以折旧价进行处理。从而,给定最优零售价格p*以及企业库存决策u*,企业最优产量为q*=y(p*-r)+u*。此时,企业期望收益为 E(Π1(p,u))=(p-c)·[u+y(p-r)]·(1-F(u))+(p-h)· (7) 求解(7)式,可得 (8) 根据(8)中的两个二阶条件,给定p值,E(Π1(p,u))为关于u的凹函数。简化分析过程,把p作为关于变量u的函数,先求解最优的u值,再求解最优零售价格p(u)以及最优产量q(p(u),u),可得如下命题。 (9) 给定u*,企业最优零售价格p*为 (10) 从而,企业的最优产量为q*=y(p*(u*)-r)+u*。 再分析政府部门的最优补贴策略。根据(1)式,政府提供固定额度补贴时,应用拉格朗日乘数法求解如下优化问题,即 (11) 在满足KKT条件下,极小化(11)式可得到该优化问题在非负约束条件下的可行解。从而,最优的r满足 E[minq*,y(p*-r)+ε]=Γ (12) 2.1.2 政府提供价格折扣的情形 采用逆向归纳法。给定价格折扣k的情况下,首先分析企业如何确定最优的p和q,然后再讨论政府如何确定折扣的问题。企业收益函数为 (13) 定义u=q-y(p-k·p),u为企业库存决策。同样,u值大于参数时,未销售出去的产品仍以折旧值进行处理。给定企业确定的最优零售价格p*,企业最优产量为q*=u+y(p*-k·p*)。此时,企业收益函数为 E(Π2(p,u))=(p-c)·[u+y(p-k·p)]· (1-F(u))+(p-h)· (h-c)·[u+y(p-k·p)]·F(u) (14) 求解(14)式,可得 (15) 显然,根据(15)式,给定p值,E(Π2(p,u))为关于u的凹函数。同样,把p作为关于变量u的函数,先求解最优u值,再求解最优零售价格p(u)以及产量q(p(u),u),可得如下命题。 (16) 给定库存决策u*,企业最优价格p*为 (17) 从而,企业确定的最优产量为q*=y(p*(u*)-k·p*(u*))+u*。 再分析政府最优价格折扣策略。根据(2)式,分析政府提供价格折扣的情况。应用拉格朗日乘数法求解如下优化问题,即 pco2·E[min(q,D(z,ε))]+ λ·{E[min(q,D(z,ε))]-Γ}} (18) 在满足KKT条件下,极小化(18)式可得该优化问题在非负约束条件下的可行解。从而,最优价格折扣k满足 E[min(q*,y(p*-k·p*)+ε)]=Γ (19) 2.2.1 政府提供固定额度补贴情形 政府提供固定额度补贴情况下,消费者实际支付额度为z=p-r。采用逆向归纳法,首先给定补贴r分析供应企业如何确定p和q问题,然后再讨论政府如何确定最优补贴r问题。企业的收益函数为 (20) 企业的期望收益即为 E(Π3(p,u))=(p-c)·[u·y(p-c)]·(1-f(u))+ (21) 求解(21)式,可得 (22) 显然,给定p值,E(Π3(p,u)为关于u的凹函数。相似的分析过程,把p作为关于变量u的函数,先求解最优的库存决策u,再求解最优零售价格p(u)以及最优产量q(p(u),u),可得如下命题: 命题3D(z,ε)为乘积形式,政府应用固定额度补贴条件下,在c>r成立时,企业最优库存决策u*由下式给定,即 (23) 给定企业最优库存决策u*,企业的最优产品价格为 (24) 最优产量为:q*=(u*·y(p(u*)-r)。 再讨论政府如何提供固定额度补贴问题。根据(1)式,应用拉格朗日乘数法求解如下优化问题,即 pco2·E[min(q,D(z,ε))]+λ· {E[min(q,D(z,ε))]-Γ}} (25) 在满足KKT条件下,极小化(25)式可得到该优化问题在非负约束条件下的可行解。从而,最优补贴r满足 E[min(q*,y(p*-r)·ε)]=Γ (26) 2.2.2 政府提供价格折扣的情形 采用逆向归纳法,首先给定价格折扣k,再研究供应企业如何确定最优的p和q,最后讨论政府部门如何确定最优价格折扣k。此时,企业收益函数为 (27) 企业的期望收益为 f(η)dη+(h-c)·[u·y(p-k·p)]·F(u) (28) 求解(28)式,可得 (29) 相似的分析过程,把p作为变量u的函数,先求解最优的u值,再求解最优销售价格p(u)以及最优产量q(p(u,)u),可得如下命题。 命题4D(z,ε)为乘积形式,政府提供价格折扣情况下,企业最优库存决策u*由下式给定,即 (30) 企业最优销售价格为 (31) 最优产量为q*=u*·y(p(u*)-k·p(u*))。 再讨论政府部门提供价格折扣的问题。根据(2)式,政府选择价格折扣方式的情况下,仍应用拉格朗日乘数法求解如下优化问题,即 (32) 在满足KKT条件下,极小化(32)式可得该优化问题在非负约束条件下的可行解。从而,最优价格折扣k满足下式 E[min(q*,y(p*-k·p*)·ε)]=Γ (33) 政府直接给生产绿色产品企业提供补贴也是常见的方式。以下将分析需求不确定性影响下政府直接给企业提供补贴政策对企业决策的影响,并且与政府直接给购买绿色产品消费者提供补贴时的情形进行比较。政府给绿色产品生产企业提供补贴将对消费者需求曲线不产生影响。假定政府对企业生产的每一单位产品提供补贴s(s≥0),其目标函数为 s.t.E[min(q(s),D(p(s),ε))]=Γ (34) 此时,政府对企业实际生产产量进行补贴,补贴与产品销量无关。给定政府补贴,供应商选择最优价格和产量实现收益最大化。从而,供应商目标函数为 (35) 此时,要获得企业最优价格和产量的闭式表达式比较困难。以下将应用数值分析方法对政府如何确定补贴,企业如何确定价格和产量问题进行探讨,并将结果与政府为消费者提供补贴的情形进行比较。 以比亚迪秦为例,2017款上市建议零售价格为18.59万元,以15%的利润率来算,成本约为c=15.8万元,销售者购买比亚迪秦将享受3.6万元政策支持(含国家补贴、地方补贴、比亚迪电动未来基金),再算上比亚迪“派送10000元纯电出行用电”活动,实际售价13.99万元。从2017年9月到2018年8月,一年的销售量为4.76万辆(数据来源于搜狐汽车网)。如前所述,表示政府提供补贴期望企业实现的目标销量,以下讨论值变化时,消费者实际支付价格、政府补贴额度、企业产量以及政府补贴额度的变化。 图3 D(z,ε)为加法形式政府提供价格折扣时的最优值 再讨论D(z,ε)为乘积形式的情形。图4中,为了把结果清晰显示出来,企业最优产量q的值仅选取了Γ∈[5,10]部分。根据图4结果,政府提供固定额度补贴,随着需求不确定性增加,政府补贴支出,企业最优产量,以及对单位产品提供的补贴都会相应增加。根据图5的结果,政府应用价格折扣方式时,随着需求不确定性增加,政府的补贴支出,企业确定的最优产量,以及对单位产品提供的补贴同样会相应增加。比较图4和图5,需求不确定性相同情况下,政府希望实现补贴支出最小化,则固定额度补贴方式为其最优选择。而且与D(z,ε)为加法形式时相似,政府提供折扣方式时,企业确定的最优产量相对较高。 图4 D(z,ε)为乘积形式政府提供固定额度补贴时的最优值 图5 D(z,ε)为乘积形式政府提供价格折扣时的最优值 政府给供应商提供补贴情形与政府直接给消费者提供补贴的情形相比较,D(z,ε)为乘积形式时政府给供应企业提供补贴的结果与需求函数为加法形式时的结果相似。以需求函数为加法形式的结果进行说明,结果如图6所示。比较图2和图6,以A=20,A=5为例,政府给绿色产品生产企业提供补贴的情况下企业最优产量较大,政府实际支付的补贴额度也比较高。因此,如果政府希望实现支出最小化,则给消费者提供固定额度补贴为其最优选择。 图2 D(z,ε)为加法形式政府提供固定额度补贴时的最优值 图6 D(z,ε)为加法形式时政府给供应企业提供补贴的最优值 研究发现,需求不确定的情况下,如果政府希望实现补贴支出最小化,则给消费者提供固定额度补贴方式为其最优选择。政府应用价格折扣时,企业最优产量相对较高。因此,如果政府希望企业提高绿色产品产量情况下,价格折扣为其最优选择。 与政府直接给购买绿色产品消费者提供固定额度补贴的情形相比,选择给供应企业提供补贴时,由于政府必须为企业分摊额外库存成本,造成了政府实际补贴支出较高的情况,因此,从政府支出最小化角度看,在市场需求不确定情况下,政府部门应该选择为消费者提供固定额度补贴。 政府应用固定额度补贴或价格折扣方式情况下,需求不确定性增加时,企业最优产量提高,政府对单位产品提供的补贴额度也会提高,消费者实际购买价格将会降低,此时,消费者购买绿色产品比较有利。 以上研究中分析的市场环境为单个企业垄断市场情形,企业在市场中自主定价并确定产品生产产量。研究中对多个企业竞争市场并没有进行探讨,结合竞争市场企业特征,分析政府如何给供应企业或者消费者提供补贴问题将会是下一步的研究重点。
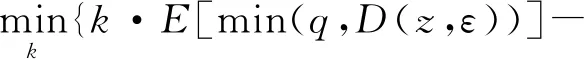

2 政府给消费者提供补贴的情形
2.1 D(z,s)为加法形式的情形

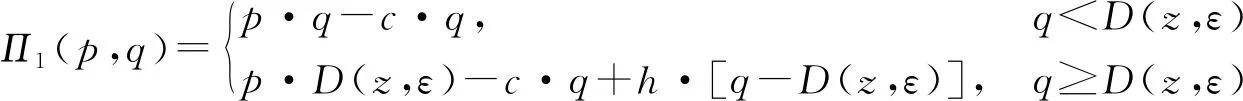
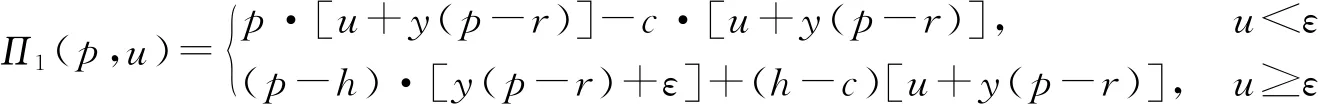








2.2 为乘积形式

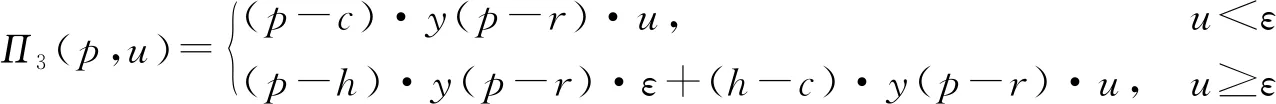


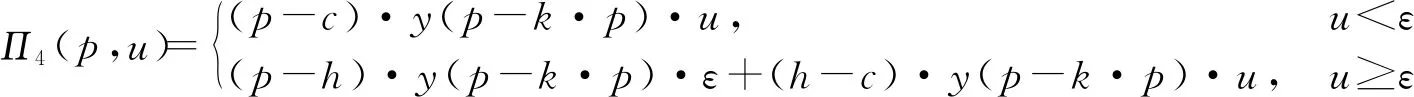


3 政府给企业提供补贴情形

4 数值分析





5 结语
