Unity内嵌Matlab子程序实现迈克尔逊干涉仪虚拟仿真实验中的干涉动态演示

邓 莉,孙 可,刘金梅,吴平颐，景培书，刘梓谊，李成渊

(1.华东师范大学 物理与电子科学学院，上海 200241；2.华东师范大学 教师教育实验教学中心，上海 200241)

2017年，LIGO团队利用类似于迈克尔逊干涉仪的精密装置探测到引力波，获得了诺贝尔物理学奖，展示了迈克尔逊干涉仪广泛的前沿科学与实际应用的广泛性和相关研究的重要意义。目前，迈克尔逊干涉现象的研究主要分为以下三类：对迈克尔逊干涉仪实验进行理论推导与误差分析的理论研究，如对实验不确定度的分析、实验误差的产生原因等[1-3]；将迈克尔逊干涉仪与其他实验相结合的创新实验，如测量金属杨氏模量、介质折射率等[4-10]；实验与计算机技术相结合，进行虚拟仿真实验模拟，如使用Labview、Python等软件模拟实验结果和数据等[11，12]。迈克尔逊干涉仪的干涉现象变化丰富，其干涉图样的形状、强度分布、干涉相互转化等都与干涉的物理原理息息相关。利用公式运算、数据分析、可视化处理于一体的信息化技术直观、准确地演示等厚干涉与等倾干涉条纹的动态变化，可以显示出物理原理与实验现象之间的联系，进一步加深对干涉原理的理解。传统的Flash、Premiere等软件，可以简单模拟实验现象，但无法解释其中的物理原理与形成机制。MATLAB软件可以将物理图像、数学计算、图形模拟相结合，动态地展示实验结果，可以准确反映出光干涉实验现象与物理原理之间的关系。

根据薄膜干涉理论，对等倾和等厚干涉现象的物理过程进行分析，探究光程差与镜面位置间的几何关系，两种干涉之间的转换原理，以及白光等厚干涉条纹产生的原因，得到相应的光强度数学表达式。在此基础上，利用MATLAB编写程序，通过改变起始条件，如波长大小、动臂反射镜位置等，实现干涉条纹变化的动态模拟，根据两种干涉条纹间转换的条件，模拟出等倾干涉圆环到等厚干涉直条纹的变化。采用Unity设计迈克尔逊干涉仪虚拟仿真实验平台，通过内嵌MATLAB子程序，可以模拟等倾干涉条纹的吞吐，等倾干涉转化为等厚干涉，不同波长光的干涉，白光干涉等一系列真实动态的实验现象。仿真实验建立在三维空间内，使用者可以自行搭建实验装置设计实验，该干涉变化的演示过程直观、形象，使实验者具有沉浸式的实验体验，增强了仿真实验的交互性，有利于加深对实验原理的理解。

1 迈克尔逊干涉仪干涉过程的理论推导

迈克尔逊干涉仪通过分振幅法，可以使一束入射光分为两束光束。由于这两束光束拥有相同的频率、振幅，并且它们的相位差保持恒定，在经过反射镜反射后能够实现干涉，得到干涉条纹[13,15-19]。如图1所示是自行研发的迈克尔逊干涉仪虚拟仿真实验的光路图。通过改变M1镜与M2镜的位置和方向，可以在观察屏上观察到不同的干涉条纹图样。

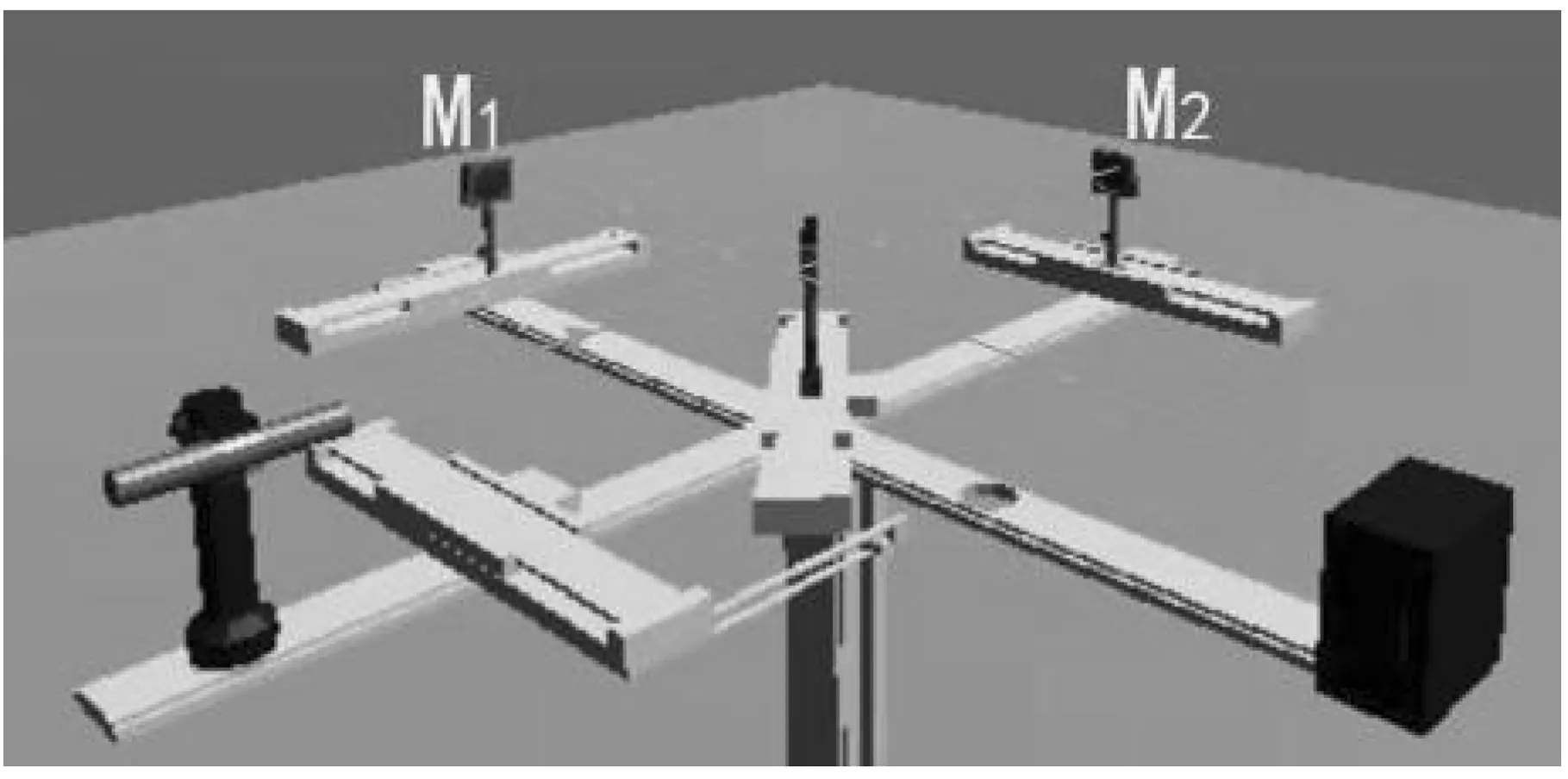
图1 自行研制的迈克尔逊干涉仪虚拟仿真实验光路

对于薄膜干涉，当入射角为i时，有光程差关系[14]：

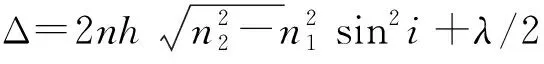
(1)

当M1镜与M2镜准确地相互垂直时，可以利用相干光得到等倾干涉条纹。此时两镜偏见厚度一致，有光程差大小为

Δ=2d·cosi+λ/2

(2)

根据得到的光程差，可以计算出相应的相位差和对应点的光强，即：

φ=2πΔ/λ；I=4cos2(φ/2)

(3)

当M1镜与M2镜不是十分垂直，两个平面将会形成一个楔形，入射光线垂直时，可以在观察屏上获得等厚干涉条纹，此时有光程差大小为：

Δ=2nh+λ/2

(4)

其中n=1。根据得到的光程差，可以计算出相应的相位差和对应点的光强，即：

φ=2πΔ/λ；I=4cos2(φ/2)

(5)

在M1镜与M2镜由相互垂直变为非垂直位置的过程中，观察屏上的条纹会由等倾干涉条纹变为等厚干涉条纹。该过程经历了入射角逐渐减小为0，以及两镜间倾角由0开始增加的两个子过程。

2 虚拟仿真实验与干涉条纹模拟

2.1 仿真实验的设计思路

将迈克尔逊干涉仪与虚拟仿真实验相结合的设计思路如下图2所示。

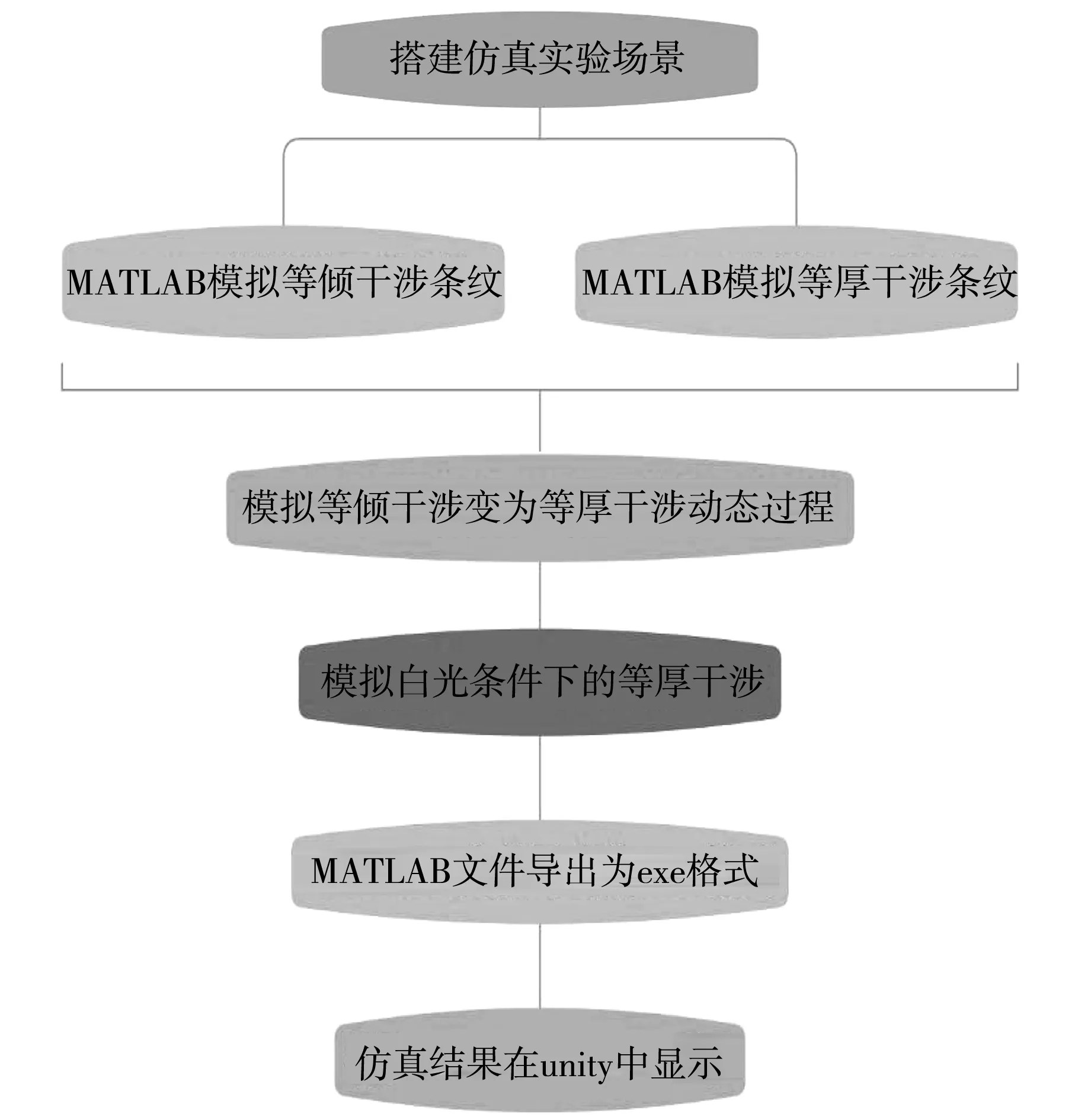
图2 设计思路图

首先在Unity中搭建出能够合理摆放实验仪器的场景，作为模拟实验结果的载体，接着使用Matlab软件对实验结果进行模拟。从等倾干涉条纹与等厚干涉条纹的模拟出发，得到这两个基础结果后再进一步实现等倾干涉变为等厚干涉这一动态过程的模拟。完成上述工作后，将光源更换为白光，模拟对应的等厚干涉条纹。最后，将所有结果导出为.exe文件格式，实现在unity中的引用。

2.2 Unity搭建实验场景

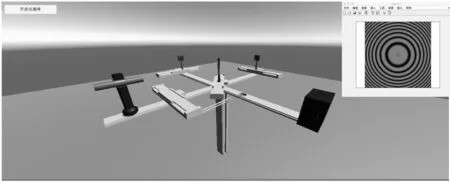
利用Unity软件进行虚拟仿真实验的设计，得到如图3(a)所示的场景与导轨。在界面左侧显示仪器库，用来存放实验中可能用到的实验装置。调用仪器库中的仪器，搭建出如图3(b)所示的迈克尔逊干涉实验的仪器图。

(a) 仿真实验场景布局

其中，每个仪器都可以点击放大，达到方便观察仪器以及调节仪器参数的目的。点击激光器，使用者可以调节不同的射出激光颜色，并且在此过程中可以阅读激光产生对应的不同材料，如选用YAG晶体加倍频晶体时可以获得绿色激光；选用砷化镓晶体可以获得红色激光；氮化镓作为增益介质则可以产生蓝色激光。改变反射镜的位置和方向，通过CCD可以在电脑显示器上观察干涉条纹。

2.3 干涉条纹的实验仿真与结果

为了使结果更具有真实感，能够准确的描述实验过程中人眼观察到的现象，为后续与虚拟仿真实验的使用相结合做准备，模拟结果需要将图案的颜色与真实情景相对应。

2.3.1 等倾干涉条纹与动态变化

首先利用MATLAB中的linspace()函数创建一定数量的数据采集点，得到一个二维的矩阵平面。设置入射光波长为633 nm，模拟红色入射光。根据等倾干涉条纹产生的原理，结合sqrt()、sin()等函数，计算二维矩阵上对应点的光强度。再经历figure()、size()、image()等函数，使光强度以图片的形式显示出来，如图4(a)所示为亮暗相间的等倾干涉条纹。

在对波长为633 μm的光干涉模拟过程中，结果应与实际中该波长的光显示的颜色相对应，即亮条纹应显示为红色。将入射光波长更改为543 μm和488 μm，对应改变程序中亮条纹区域的RGB值，使其只显示绿色或蓝色成分，完成模拟绿色入射光和蓝色入射光条件下的干涉圆环效果。同样的，改变入射光波长为543 nm和488 nm，分别模拟绿色入射光和蓝色入射光，得到如图4(b)(c)所示的图案。由等倾干涉原理的分析可知，当入射光波长减小时，干涉圆环的半径也会减小，同时干涉条纹间隔减小，即图4所示的模拟结果与理论分析相一致。

(a) 630 nm入射光干涉圆环

计算等倾干涉条纹间距得到：

(6)

可以发现当光源到观察屏的距离f远远大于干涉圆环半径r时，随着半径增加，条纹间距在不断减小，图4中三幅结果图都表现出中间稀疏边缘密集的特点，也能证明这一结论。对比图4(a)、(b)、(c)三幅图，还可以发现当入射光波长减小时，干涉圆环的半径也会减小，这与实际的理论分析也是保持一致的，验证了模拟结果的准确性。

(a)

若想得到“吐出”条的纹变化现象，只需改变动臂移动的方向，而其余条件保持不变，同样采用for循环语句进行实现。最后，为了方便对结果图的保存与在后续研究中的使用，结合MATLAB软件中动态图像输出命令将结果保存输出为“.gif”格式的动态图片。

2.3.2 等厚干涉条纹模拟

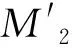
(a) M1镜与镜不相交时的干涉条纹

根据等倾干涉变为等厚干涉条纹这两个子过程的模拟以及薄膜干涉的理论分析，利用一定的MATLAB语句函数对这两个过程进行处理，得到等倾干涉变为等厚干涉完整的动态变化过程。如图7所示，图像展示了迈克尔逊干涉仪由等倾干涉变为等厚干涉这一过程中条纹形态动态变化的部分时刻。

(a)

2.3.3 白光条件下的等厚干涉条纹模拟

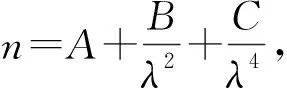
图8 白光光源条件下的等厚干涉条纹

3 利用Unity内嵌Matlab子程序实现动态干涉条纹在虚拟实验场景中的演示

通过Unity软件应用MATLAB程序的过程如图9所示。

(a) MATLAB导出可执行性文件流程图

在MATLAB软件的APP栏中选择“Application Compiler”选项，导入需要转换的主程序“.m”文件，选择“Runtime download from web”后点击Package按键导出可执行性文件，以备在unity中的使用，具体过程如图10(a)所示。在unity中首先通过using语句引入命名空间，接着在场景中创建按钮，使得仿真场景中的按钮被点击后能对应显示MATLAB程序运行结果，最后创建路径，引入可执行性文件，完成MATLAB结果在unity中的使用。在Matlab中将文件导出为.exe格式，得到unity可执行的文件。在虚拟仿真实验场景中，选择显示CCD采集结果的软件，得到如图10(a)、(b)、(c)所示的干涉图像，改变动臂长和反光镜方向，干涉图像也会随之变化。进一步测量不同位置的等厚干涉光强分布图，如图10(b)所示，与实际实验结果一致，证明仿真实验的可行性与准确性。

调节M1镜与M2镜准确地相互垂直，在屏幕上获得等倾干涉条纹，如图10(a)所示；而M1镜与M2镜不相互垂直时，在屏幕上会获得等厚干涉条纹，如10(b)所示，更换光源，屏幕上获得白光干涉条纹，虚拟仿真实验结果均与实际实验中观察到的现象完全一致。

(a) 等倾干涉

4 结 语

根据对迈克尔逊干涉仪产生干涉现象的原因进行理论分析，结合Matlab软件对实验过程中的几种干涉图样进行模拟，得到了结果与实际结果完全一致的效果图，保证了仿真模拟的真实性。在此基础上与unity软件相结合，搭建虚拟仿真实验平台，既可以清晰的展现实验的结果，也可以为使用者提供清晰的理论指导，使他们更加直观、深刻的理解产生干涉的具体过程，同时提高使用者与仿真实验的互动感。虚拟仿真实验不仅可以拓宽迈克尔逊干涉仪的使用，而且当与其他实验相结合提高实验的综合性与拓展性。