基于传感器的液体粘滞系数测量装置设计
2022-10-20秦之斌李嘉蕊
秦之斌,李嘉蕊,张 斯,周 芸,张 华
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
液体的粘滞系数又称为内摩擦系数或粘度,是描述液体内摩擦力性质的一个重要物理量,并对生产生活有着实际意义,在航海、造船、运输、化学和医学上都有许多应用。
目前有许多方法用于测量液体粘滞系数,如落球法,毛细管法以及转筒法等。毛细管法实验搭建较为简单,但装置易受外界环境影响,且可重复率较低[1]。转筒法则利用力矩和转速与粘滞系数的关系进行计算,但测量误差较大,实验装置成本较高不适合实验室教学使用[2]。
大学物理实验教学中普遍采用传统落球法测量液体的粘滞系数,用秒表计时或激光发射器计算小球运动时间等参数[3],再利用公式计算液体粘滞系数。但实际实验操作中,人工计时的方法存在视觉和反应上的偏差,运动时间测量结果误差较大;激光发射器测量的原理是利用激光被遮挡的时间间隔进行计时,但激光光束较窄,且在实验中常选择直径较小的小球,小球有较高几率不遮挡激光,进而导致实验失败[4]。此外,以上方法均只能计算透明液体的粘滞系数。
本文主要研究基于传感器和单片机,设计液体粘滞系数测量装置,将计时部分改进为传感器和单片机计时装置,即传感器感应金属小球下落瞬间进行计时,配合单片机显示时间结果,应用计算机计算液体粘滞系数。测量过程直观、准确,测量计算所得粘滞系数误差较小。因改进装置结构的特殊性,该装置还适用于测量不透明液体的粘滞系数,拓宽了液体的检测范围,具有普遍意义。
1 设计原理
在静止液体中缓慢下落的小球在竖直方向上可视为受到重力P、浮力ρgV和阻力f三个力的作用,如图1所示。当物体的运动速度足够小时,压差阻力远小于粘性阻力,此时可认为阻力等于粘滞阻力F[5]。
粘滞阻力F是液体密度、温度和运动状态的函数。利用斯托克斯公式
F=6πηvr
(1)
可求出液体的粘滞系数(式中η为液体密度,v为小球运动速度,r为小球半径)。
(2)
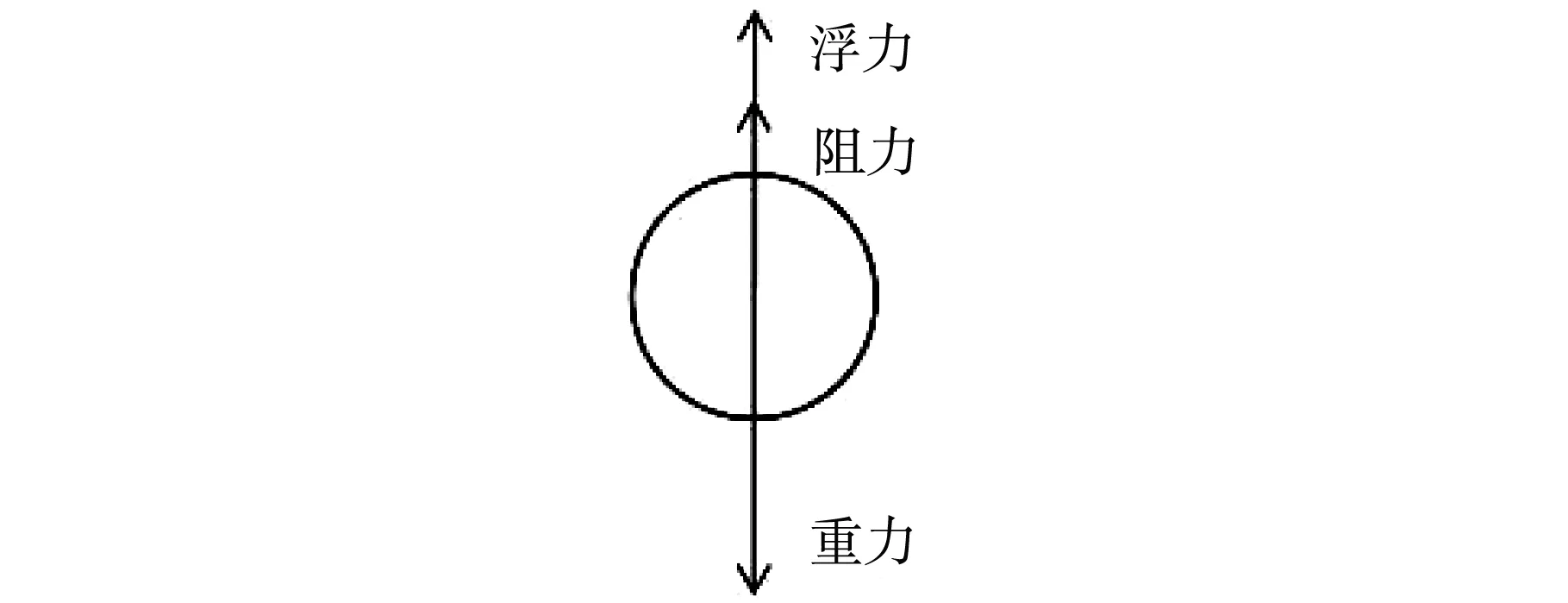
图1 物体受力图示
即可求得粘滞系数:
(3)
当0.1
2 实验装置的设计
实验装置由计时装置和检测装置构成,如图2所示。
(1)计时装置:
计时装置由单片机、金属传感器、15 V恒压直流电源、电压转换电路组成。
根据设计要求编写秒表计时程序并下载到单片机中,绘制单片机电路原理图如图3所示,转印并焊接完成电路。设计制作电压转换电路,将传感器感应金属时输出的15 V电压转换为单片机可接收的5 V电压,完成传感器与单片机的连接。
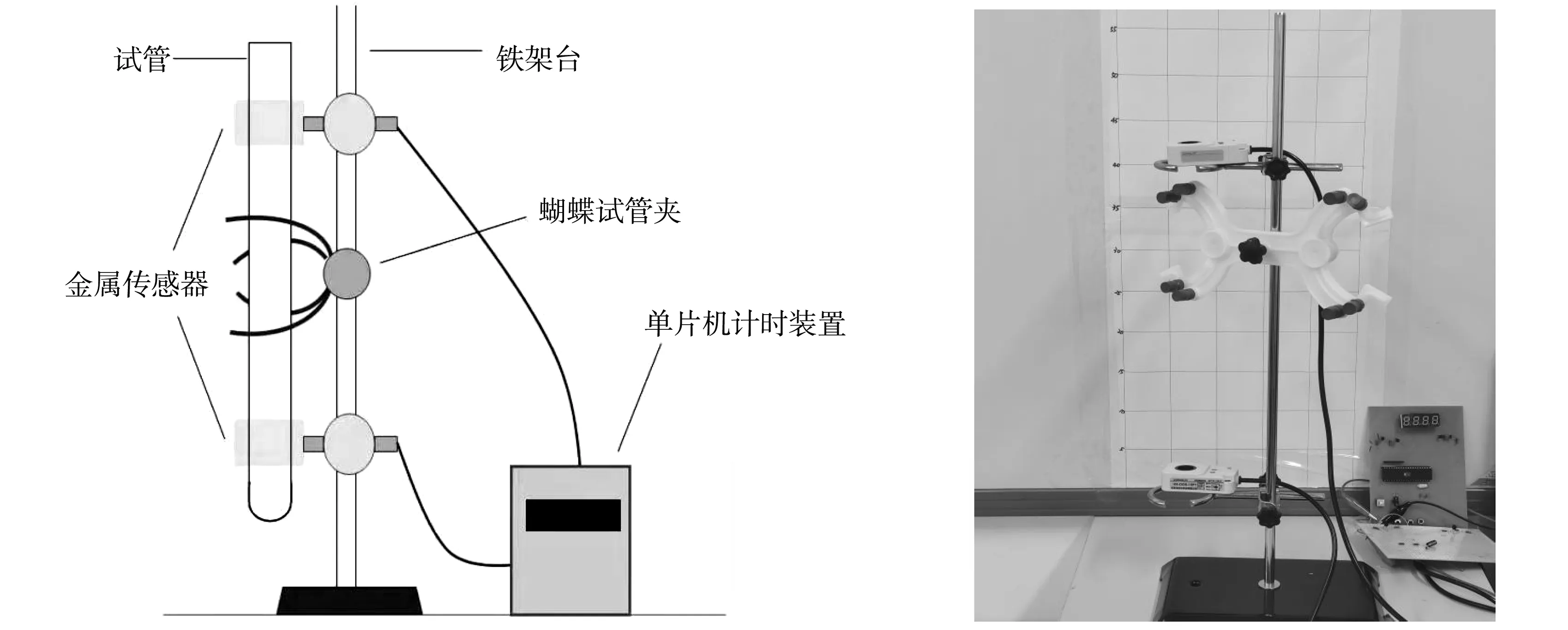
图2 实验装置图和实物图

图3 单片机原理图
(2)检测装置:
检测装置由铁架台、试管夹、直径均为14 mm长分别为1 m、0.3 m的试管①和试管②、待测液体(蓖麻油)、直径分别为2 mm、2.5 mm、2.78 mm、3 mm、3.2 mm、3.5 mm、4 mm的表面光滑金属小球和距离刻度纸组成。
安装铁架台和传感器,调节传感器位置。准备试管、不同直径金属小球和实验液体蓖麻油。实物图如图2所示。
3 粘滞系数影响因素探究
实验流程如图4所示:

图4 实验步骤流程图
3.1 探究小球直径对粘滞系数测量的影响
根据实验要求,实验步骤如下:
首先对①号试管进行实验。调节传感器距试管底初始距离为2 cm,两传感器间间距为15 cm。记录不同小球落下时的单片机示数,即小球经过两个传感器的时间间隔。计算液体粘滞系数,利用实验温度下的标准粘滞系数0.83计算误差。
为探究不同液面高度对相同变量的影响,对②号试管进行实验,设定初始传感器距试管底距离为2 cm,两传感器间间距为40 cm。
根据上述部分进行实验,得到数据如表1所示。

表1 小球直径对粘滞系数测量的影响
小球直径对粘滞系数的影响如图5所示。由图可知,直径为3mm的小球误差最小,最小误差为19.86%。下述实验均以3mm直径小球进行实验。

图5 小球直径对粘滞系数测量的影响
3.2 探究传感器距底端距离对粘滞系数测量的影响
根据实验要求,实验步骤如下:
保持两试管传感器间距和液面高度不变,分别对①号试管和②号试管探究,均设传感器距试管底初始距离为1cm,距离改变步长为0.5cm。
根据上述部分进行实验,得到数据如表2、表3所示。
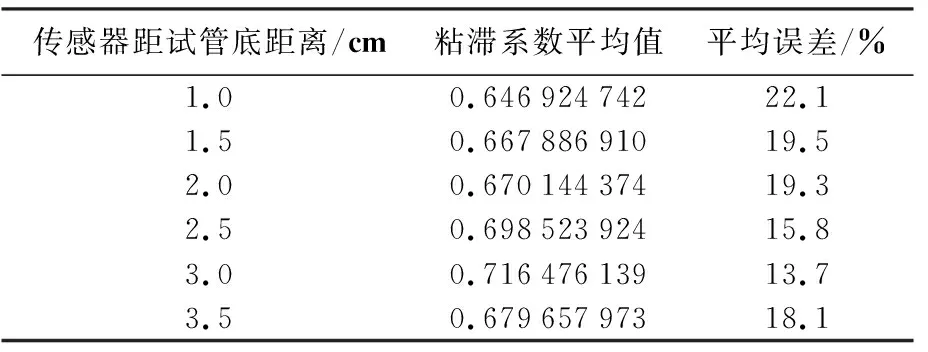
表2 30 cm试管传感器距底端距离对粘滞系数测量的影响
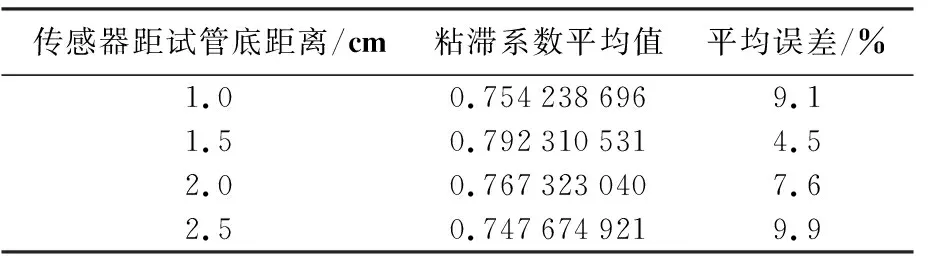
表3 100 cm试管传感器距底端距离对粘滞系数测量的影响
下端距管底距离对粘滞系数的影响如图6所示:可知对于0.3m试管,传感器距试管底距离为3cm时误差最小,为13.68%;对于100cm试管传感器距试管底距离为1.5cm时误差最小,为4.54%。下述实验选此数据进行实验。
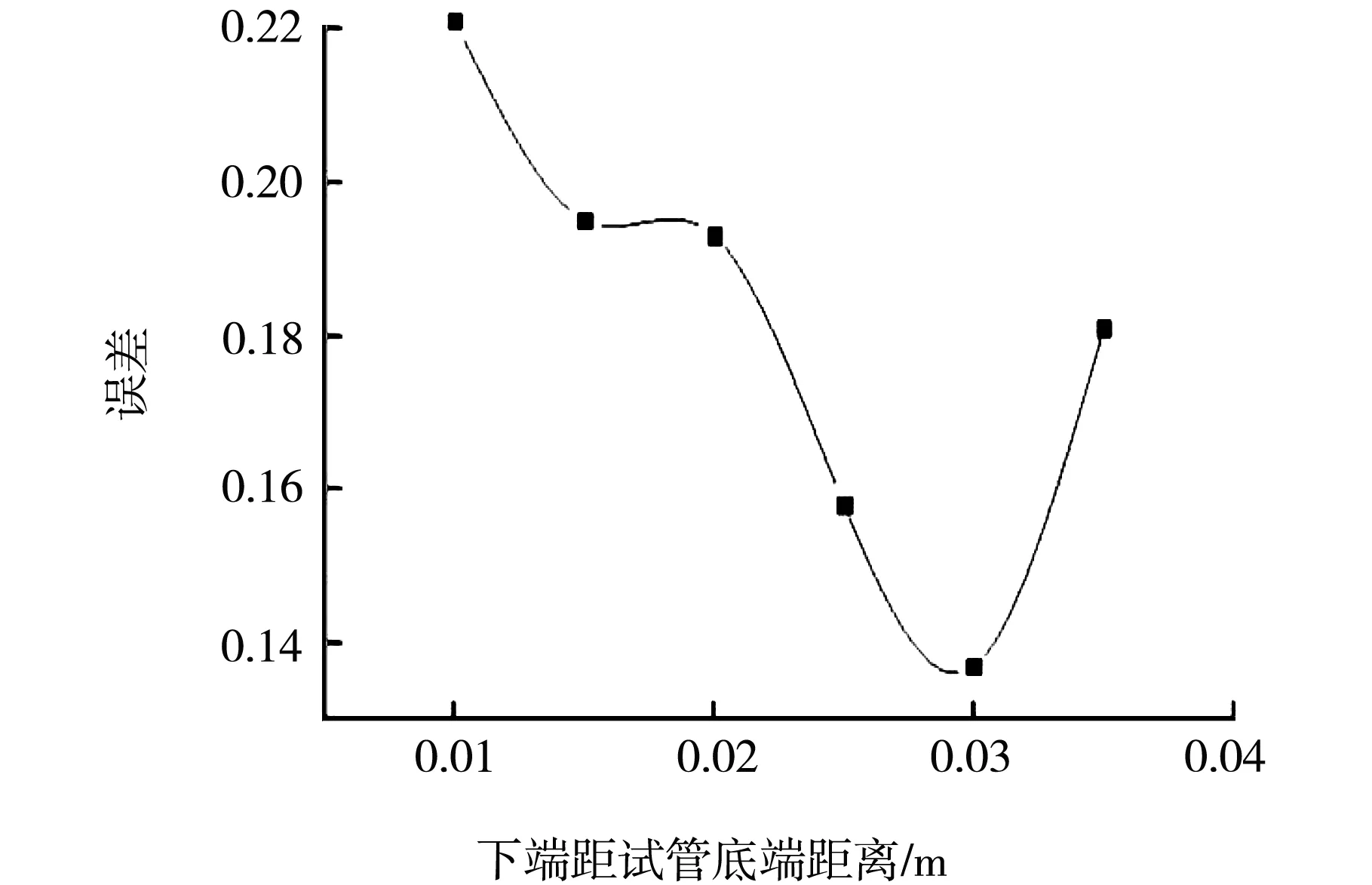
(a)
3.3 探究小球运动距离对粘滞系数的影响
根据实验要求,实验步骤如下:
设①号试管和②号试管两传感器间初始间距为15cm和40cm,分别以1cm和5cm为步长改变传感器间距离进行实验。
根据上述部分进行实验,得到数据如表4、表5所示。

表4 30 cm试管运动距离对粘滞系数误差的影响
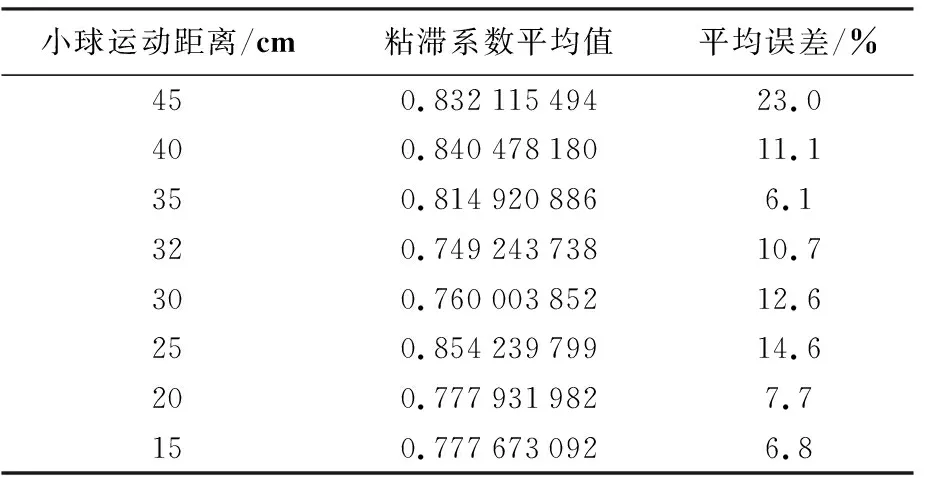
表5 100 cm试管运动距离对粘滞系数误差的影响
小球不同运动距离对粘滞系数的影响如图7所示。
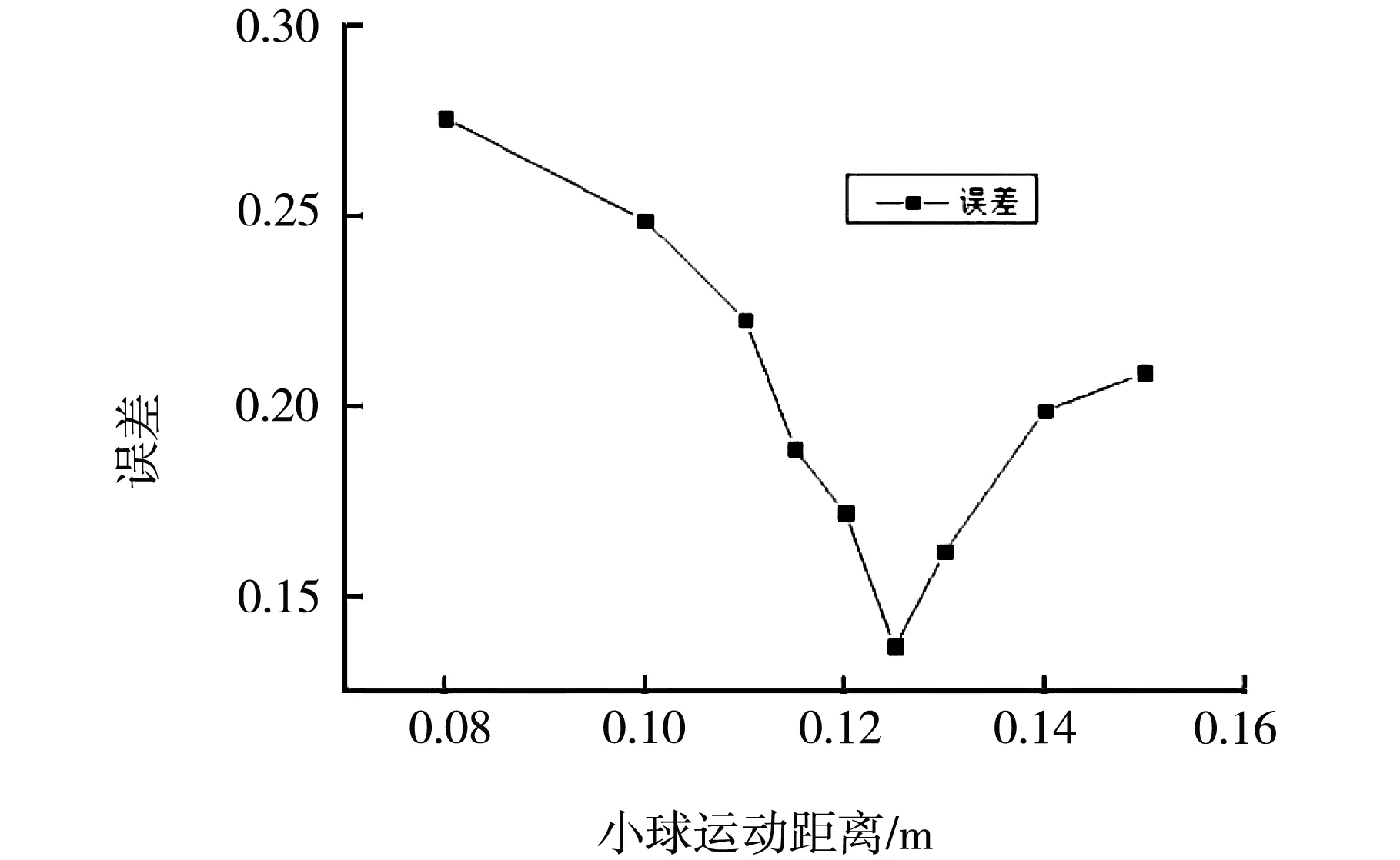
(a)
可知对于30cm试管小球运动距离为12.5cm时误差最小,为13.65%;对于100cm试管,在运动距离大于25cm时,在35cm处出现最小误差6.09%,当运动距离小于25cm时,误差随运动距离的减小而减小,逐渐稳定在6.6%左右。综合考虑数据结果与实验操作可行性,选择运动距离为35cm作为实验结果。
3.4 探究不同液面高度对相同变量的影响
两种试管结果对比如表6所示。

表6 30 cm试管与100 cm试管实验误差对比
由表6可知,当传感器距试管底距离和运动距离变化时,100cm试管实验误差均小于30cm试管。
4 液体粘滞系数的测量
4.1 与实验室方法的比较
根据实验要求,实验步骤如下:
取上述实验最优值设置实验参数,使用手机秒表记录小球运动时间数据。
根据上述部分进行实验,得到数据如表7所示。

表7 两种方法误差对比
由实验数据比较可看出,传统方法测量计算液体粘滞系数平均误差为21.0%,采用改进实验装置测量计算平均误差为6.42%,可显著减小实验误差。
4.2 测定不透明液体粘滞系数
根据实验要求,实验步骤如下:
为模拟不透明液体,将100cm试管用不透明胶布缠绕。同样取实验最优值设置实验参数,使用传感器配合单片机计时。
根据上述部分进行实验,得到数据如表8所示。

表8 不透明情况与透明情况对比
由实验数据比较结果可知,采用改进实验装置可以测量不透明液体粘滞系数,且粘滞系数平均误差为8.03%,透明液体粘滞系数平均误差为6.42%,没有明显变化。
5 结 语
本文设计了一种基于传感器的液体粘滞系数测量装置,基于单片机和传感器等硬件控制电路,研究了一种新型的液体粘滞系数测量方法。通过装置测量出时间差、小球运行距离,结合实验参数带入公式中计算粘滞系数。
该装置与传统落球法测量装置相比,具有误差较小、操作简单、使用范围广、集成度和智能化程度高、数据处理更精准等特点,同时克服了实验室传统落球法测量装置无法测量不透明液体的缺陷,拓宽了液体的检测范围,具有普遍意义。
