“唱歌铁氧体”振动规律的研究

买子桐，贺西平，陈一凡，汤衍鹏，李增明，张 晨，解邦鑫

(陕西师范大学 物理学与信息技术学院，陕西 西安 710119)

磁致伸缩效应是铁磁体在外磁场变化时，长度及体积均发生变化的现象。传统的磁致伸缩材料，磁致伸缩系数一般为30～60 ppm。依据材料特性可将磁致伸缩材料分为两类，一类是纯金属磁致伸缩材料，如镍、铁钴合金、镍铁合金等。这类材料因具有高机械强度、居里点及工作性能稳定，在声纳系统中得到了广泛的应用。另一类是铁氧体金属材料，如镍锌铁氧体，这种材料具有高灵敏度，涡流和磁滞损耗都较小，可被用作水听器[1]。相较于传统磁致伸缩材料，上世纪七八十年代以来发现的稀土超磁致伸缩材料及铁镓合金则具有更大磁致伸缩系数(1 500～2 000 ppm)，被称作超磁致伸缩材料[2,3]。与应变系数为250～400 ppm的PZT压电陶瓷相比，超磁致伸缩材料不仅应变值更大，还具有更大的机电耦合系数、更低的声速，有利于换能器的小型化设计[2]。

2020年中国大学生物理学术竞赛(2020CUPT)第四题为“唱歌的铁氧体”：“铁氧体棒插入信号发生器供电的线圈中。在某些频率下，铁氧体棒开始发出声音，试研究这一现象。”事实上，铁氧体棒之所以能“唱歌”，是因为该棒为磁致伸缩材料，在交变电流激发的交变磁场中会产生磁致伸缩振动，从而发出“歌声”。类似的现象如，变压器的噪声就是变压器线圈中用作铁芯的铁氧体磁致伸缩产生的[4]。

本文计算了铁氧体棒的共振频率和应力、位移分布。测试了三根相同直径、不同长度的镍锌铁氧体棒的振动模态、共振频率及电压和振幅的规律。分析了雾化现象及断裂位置。

1 铁氧体棒振动频率、位移分布及应力分布

实际应用中，为避免产生倍频现象并有更大的振幅，一般要给予磁致伸缩材料适当的偏置磁场，使其工作在线性区域。

1.1 共振频率

假设一良导磁体与N匝线圈所缠绕的铁氧体棒形成闭合磁路，输入电动势的角频率为ω，铁氧体棒的横截面积为S。

激励电源、线圈构成的电路中，电压由激励电压E，主磁通产生的电动势e、漏磁通产生的电动势δe构成，通电线圈内阻产生电压降iR，由电路中的基尔霍夫定律，

E=iR-e-δe

式中，线圈内阻R一般较小。若忽略线圈内阻与漏磁通，上式可以写为，

E=-e

(1)

即，

E=jωNB3S

(2)

(2)式中B3为通过铁氧体棒的磁通密度，下角标3代表z方向，这里省略了时间变化项e-jωt。

存在偏置磁场，磁致伸缩材料的应变与其内部的磁场满足线性压磁方程[5]

(3)

(4)

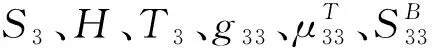
由此，得到棒中的应力为，

(5)

棒纵振动的微分方程为[6]，

(6)

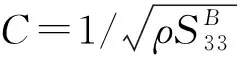
ξ=Asin(kz)+Bcos(kz)

(7)

其中k=ω/C。由两端位移边界条件，

z=0端：ξz=0=ξ0得B=ξ0

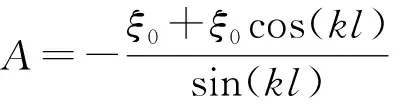
(8)

代入式(7)中得，

(9)

棒的两端不受外力，处于自由边界条件，

0=-ST3z=0=-ST3z=l

代(5)式和(8)式入(9)式中得，

(10)

由此得铁氧体棒的位移方程，

(11)

加入时间变化项有，

(12)

可以看出，振幅与激励电压的幅值，压磁常数成正比，与线圈匝数、波数、棒横截面积成反比。

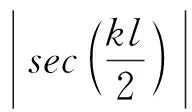
(13)

式中f0为棒的共振频率，当激励频率达到棒的共振频率时，棒的位移振幅最大。若考虑阻尼，设衰减因子为γ，则考虑阻尼后的共振频率可以表示为[7]

(14)

可以看到，受阻尼的影响，棒实际的共振频率比未考虑阻尼时的共振频率要小一些。

1.2 位移、应力分布

由(12)、(13)式知，棒共振时的位移和应力分布为，

(15)

(16)

根据以上两式，铁氧体棒沿轴向方向的归一化分布规律如图1所示。

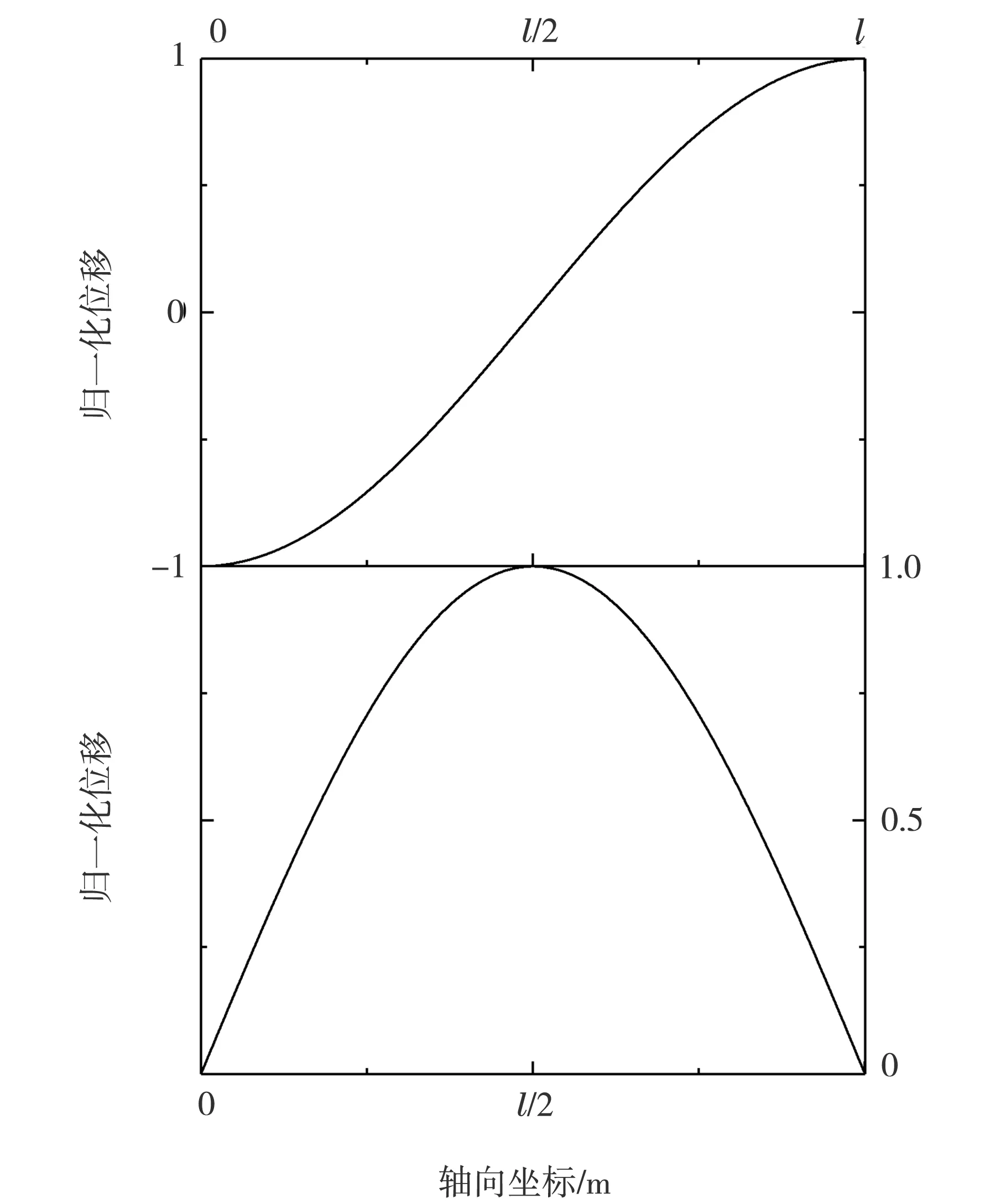
图1 位移、应力分布曲线

可以看到，铁氧体棒的位移在棒的两端最大，应力在棒中间位置，也即l/2处最大。

2 实验测试

实验系统由日本产型号为NF BP4620的双极性电源、线圈、镍锌铁氧体棒、浙江产的LV-S01测振仪、Polytec PSV-400扫描式激光测振仪、PC机组成。后两者分别用于面扫和单点式扫描测振实验，如图2(a)和(b)。

(a) 面扫实验装置

双极性电源为线圈提供直流偏置磁场和交流激励电压，线圈中的镍锌铁氧体在交变磁场的作用下进行振动。激光测振仪探头发射的激光入射到镍锌铁氧体端面，反射的激光也由探头接收，激光测振仪将光信息转换为电信号在PC机中经软件进行分析处理，后将镍锌铁氧体棒的振动频域图像展示在屏幕上。

先后对三根相同直径(10 mm)不同长度(180 mm、140 mm、120 mm)镍锌铁氧体棒(记为l1、l2、l3)进行了振动测试。

2.1 振动模态

利用图2(a)中的Polytec PSV-400扫描式激光测振仪测得三根镍锌铁氧体棒l1、l2、l3的振动模态为纵振动，三根棒的基频分别为14.09 kHz、17.641 kHz、20.91 kHz。图3中显示了l2振幅最大处对应的振动频率为17.64 kHz。

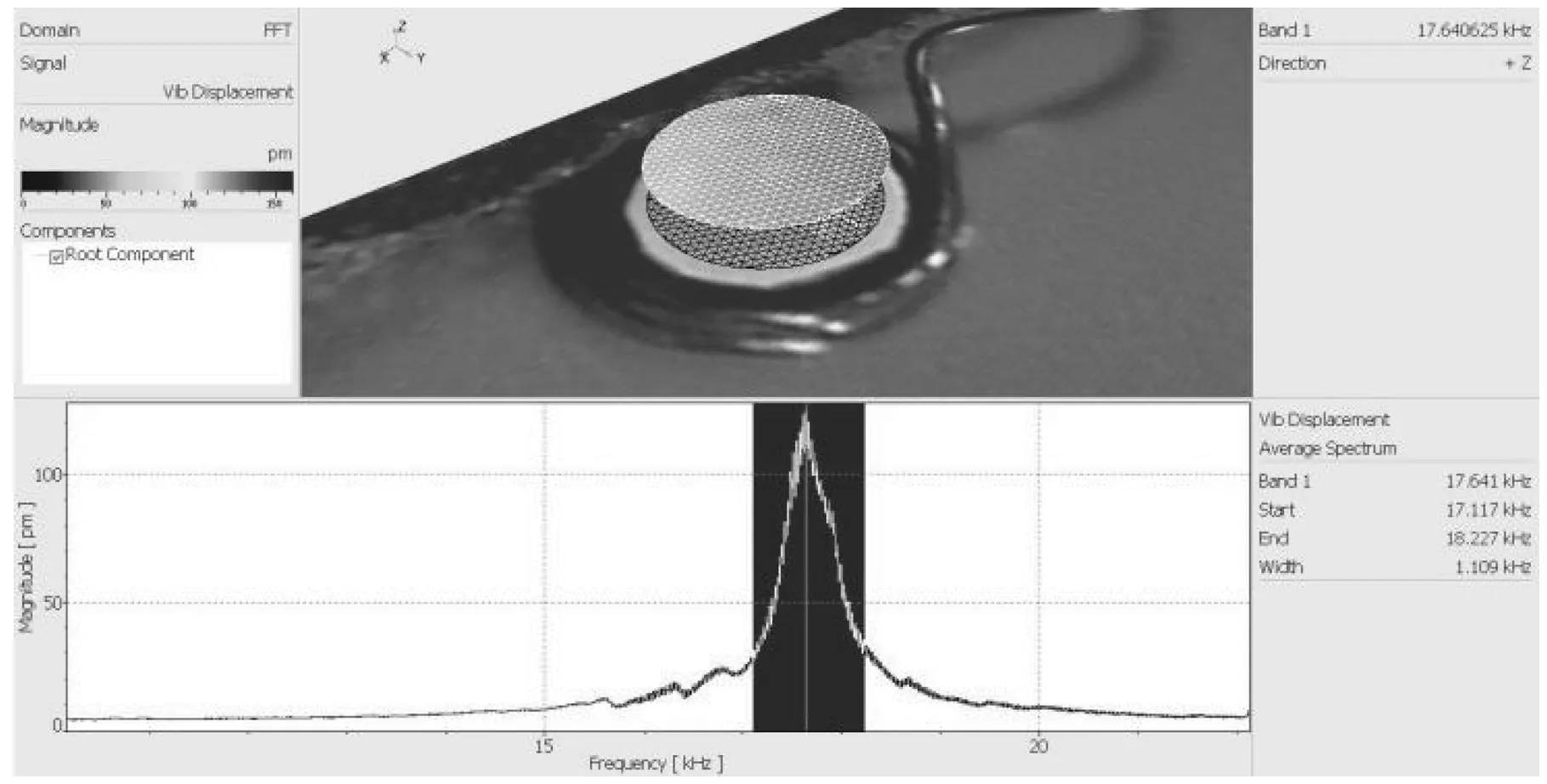
图3 镍锌铁氧体棒的振动模态

2.2 振幅-频率曲线

利用图2(b)中的单点式扫实验装置测试镍锌铁氧体棒的振幅-频率曲线。

调节电源，输入0.84 V的偏置直流电压及5 V的交流电压，频率从1 kHz调起，以0.5 kHz为步长调至25 kHz，记录镍锌铁氧体棒的振幅和对应的频率。找到振幅最大点的大概频率范围，再在振幅最大点附近内减小步长，精确找到三根镍锌铁氧体棒的共振频率。测得的振幅-频率曲线如图4所示。

由图4也可以看出，l1、l2、l3的共振频率分别为13.60 kHz、17.60 kHz、20.40 kHz，与激光测振所得的频率的偏差分别为3.58%、0.23%、2.48%。

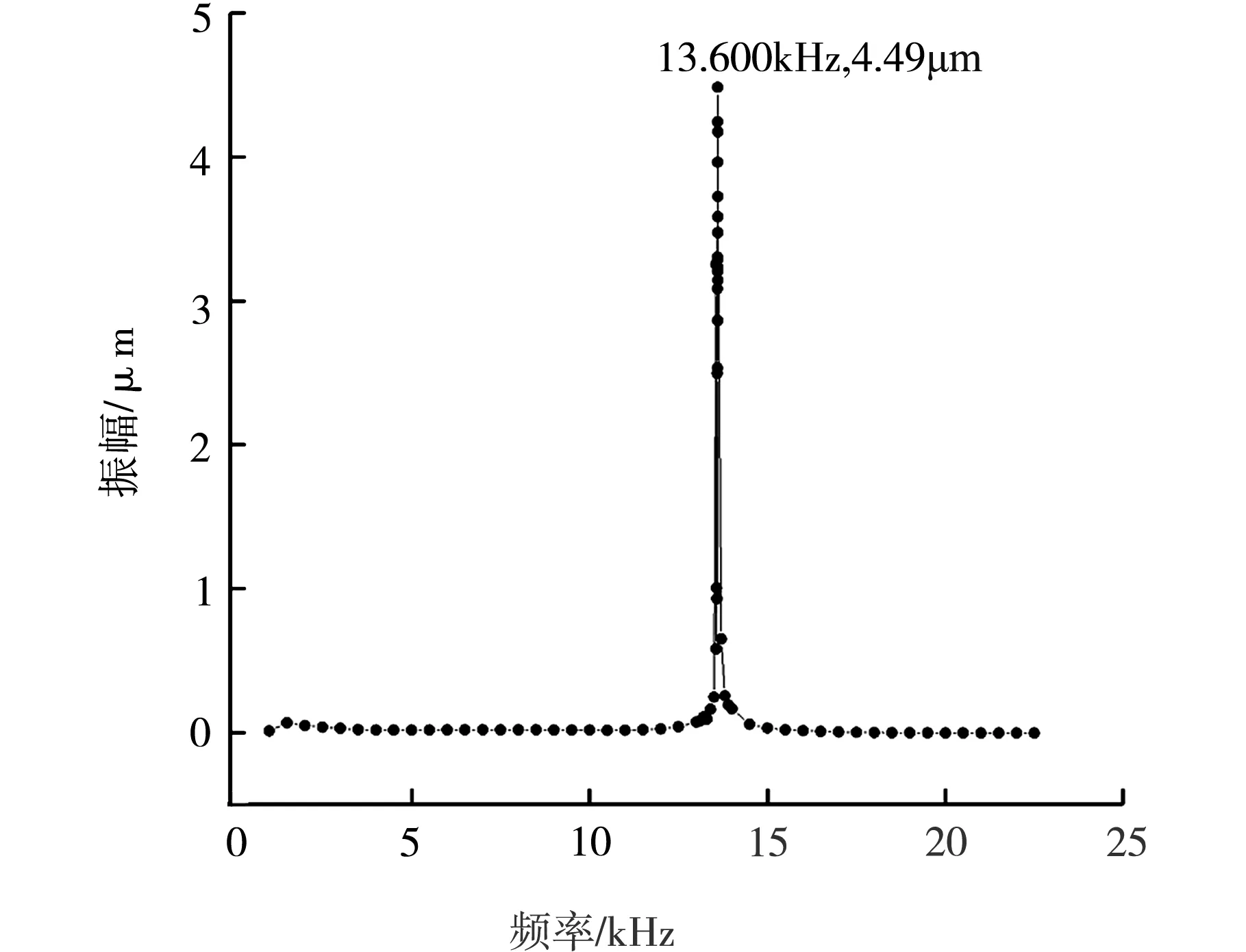
(a) l1的振幅-频率曲线

2.3 共振频率下的振幅-电压曲线

根据磁致伸缩材料的非线性本构关系[7]，在一定偏置磁场下，当交变磁场的磁场强度超过某一阈值时，磁致伸缩材料的振幅与电压不再呈近似线性变化关系，这个阈值与材料的特性有关，而外加电压的大小直接影响了棒中磁场强度的大小。

调节电源，输入直流电压仍为0.84 V，交流信号的激励频率分别为l1、l2、l3单点扫描装置所测得的共振频率，电压幅值从5 V起开始调节，步长为5 V，调至仪器能输出的最大电压120 V，得到三根棒在各自共振频率下的振幅-电压曲线，如图5所示。

从图5可以看出，三根镍锌铁氧体棒在40 V以下的振幅与电压呈较好的线性关系，随着电压的增大，二者将不再满足近似线性关系。

(a) l1的振幅-电压曲线

3 分析与讨论

3.1 共振频率的理论与实验对比

代三根镍锌铁氧体棒的相关参数入(13)式，计算得其共振频率。理论计算值与实验值(以单点测振仪测得的实验值作为比较基准)及相对误差ε如表1所示。

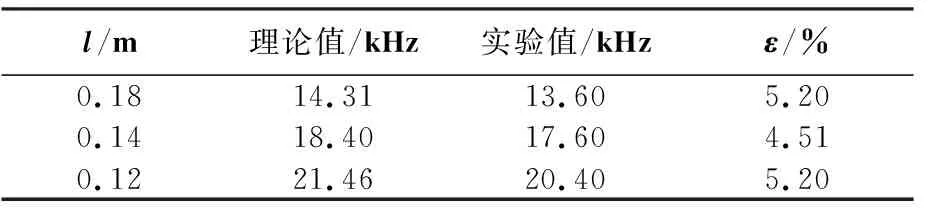
表1 镍锌铁氧体棒的共振频率

可以看到，三根镍锌铁氧体棒共振频率的实验值都比理论值小一些，在1.1中已经分析过，这是由于理论计算中忽略了阻尼。实验值比理论值要小5%左右。由式估算得到三根棒的阻尼系数分别为0.31、0.29、0.31。根据文献[8]的计算方法，可以先用(13)式计算得到铁氧体棒共振频率，再令阻尼系数为0.30，结合(14)式就可以估算出铁氧体棒的共振频率。

3.2 雾化现象

镍锌铁氧体棒的振幅达到1μm即可观察到超声雾化现象，振幅越大，现象越明显。图6是当输入交流电压为60V时，采用英国产Photron牌型号为FASTCAMMini高速摄像机拍摄l1的雾化图，此时棒的振幅为13μm。

图6 超声雾化图像

3.2 断裂现象

交流电压为65V时，l1的振幅达到了16μm，工作1min左右断裂。图7(a)、(b)是l1断裂前后的情形，测量断面在轴向的位置坐标为93.94mm，约在棒的中心位置，与理论计算所得的棒中点位置偏差为4.38%，图7(c)将实际断裂位置与归一化的应力分布曲线进行对照，可以看到，实际断裂位置与理论计算的位置相近。

(a) 断裂前

4 结 语

铁氧体棒唱歌现象产生的物理机制是磁致伸缩，交流线圈产生交变磁场，铁氧体在交变磁场中因磁致伸缩而振动。有偏置磁场的情况下，其振动的频率与激励频率相同，激励频率达到共振频率时，具有最大振幅。本文计算了铁氧体棒的共振频率及位移、应力分布，测试了铁氧体棒的纵振动模态、振幅-频率关系以及振幅-电压关系，并对棒的断裂位置进行测量分析，实验与计算结果基本吻合。