等腰三角形界面缺陷对复合绝缘子电场分布的影响

沈 浩，刘 辉，马新明，符一凡，章敏俊，杨福兴，张 豪，廖敏夫

（1.国网山东省电力公司电力科学研究院，山东 济南 250003；2.大连理工大学 电气工程学院，辽宁 大连 116024）

0 引言

自“十二五”规划以来，我国的电力行业着重于特高压电网的研究和布局工作。大量的运行数据表明，复合绝缘子具有尺寸小、质量轻、耐脏污、机械强度和绝缘性能高等优点，目前已被广泛地应用于我国的高压输电线路中[1-3]。但复合绝缘子的轴向电场分布极其不均匀，高、低压侧端部承受了较高的电场强度[4-6]。护套与芯棒在高场强的长期作用下逐渐老化，出现缺陷，导致其附近的局部电场严重畸变，发生局部放电，对输电线路的安全造成极大威胁。目前的研究发现界面缺陷主要出现在复合绝缘子的高压侧部位，并逐渐向中段部位和低压侧部位发展[7-9]。

文献[10]建立了护套和芯棒分离发展的模型，得出了界面缺陷会由高压侧逐渐向中段和低压侧发展的结论，但未对发展过程中的场强变化做进一步研究。文献[11]指出水隙缺陷部位的场强减小且存在边缘效应，易引起局部烧蚀，但该研究建立的是二维轴对称模型，即缺陷为环绕芯棒一周的环形缺陷，与实际情况有所差异。文献[12-13]建立了界面缺陷的球形和弧形柱体模型，研究了不同尺寸的缺陷对电场分布的影响，并通过改变缺陷部位的材料参数来模拟空气、水气、酸液等杂质对电场分布的影响，但实际剖检后的界面缺陷常常为树枝状，球形和弧形柱体模型与实际形状有所差异。文献[14-15]虽然研究了气隙和水隙缺陷的不同特点，但水气浸入缺陷是一个缓慢变化的过程，仅在空气和水条件下研究不够全面。

本文利用SOLIDWORKS软件建立500 kV复合绝缘子的三维模型，通过COMSOL软件对等腰三角形界面缺陷和弧形柱体界面缺陷进行仿真和对比，研究缺陷尺寸和水气浸入对复合绝缘子轴向电场分布及界面缺陷发展过程的影响。

1 模型的构建与简化

1.1 复合绝缘子建模

本文根据FXBW-500/210型棒形悬式复合绝缘子进行建模仿真，其详细的结构参数如表1所示。该复合绝缘子的高、低压侧端部设有均压环，环径分别为350 mm和370 mm。图1为SOLIDWORKS软件中建立的复合绝缘子简化模型。

图1 复合绝缘子简化模型Fig.1 Simplified model of composite insulator

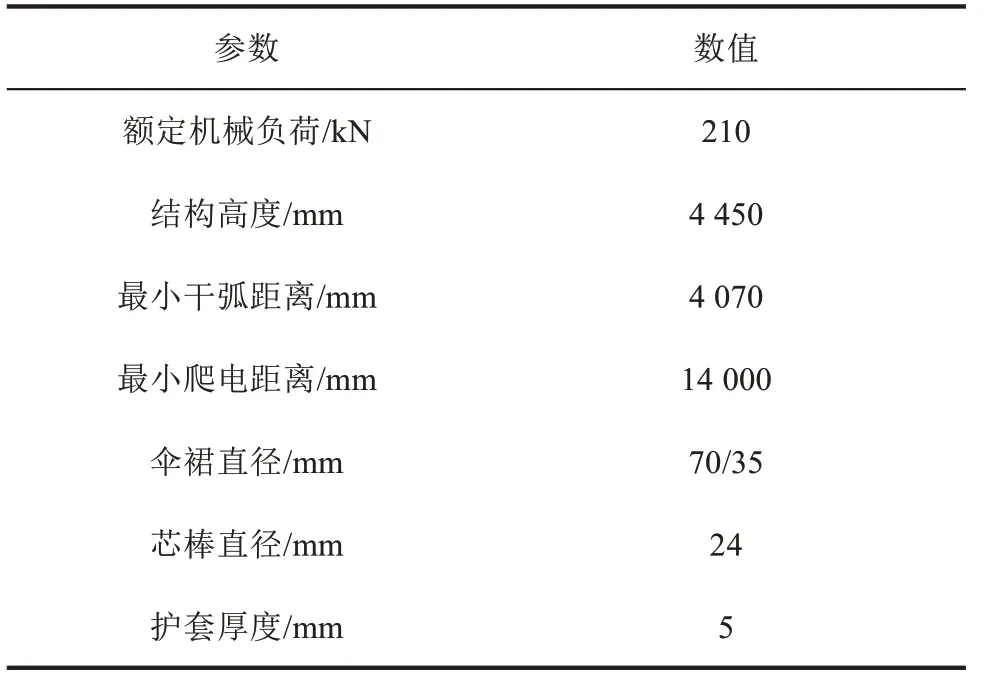
表1 FXBW-500/210结构参数Tab.1 Structural parameters of FXBW-500/210

本文主要对复合绝缘子内部界面缺陷进行研究，因此可忽略杆塔、导线以便于简化模型。在实际的输电线路中，工频交流电属于低频范畴，瞬时电场受到的影响可以忽略不计，因此本文可以按照静态场进行仿真分析[16]。

在实际中绝缘子周围的电场分布为无限远域，通过在距离其较远的位置设置电位为0的人工边界，将问题转换成有限元域进行分析。本文设置尺寸为10 m×10 m×20 m的长方体域作为远场域。

1.2 界面缺陷建模

复合绝缘子在加工过程中存在脱模剂渗出等问题，导致界面粘结不良，且高压侧承受较大的电场强度，因此其界面缺陷通常呈树枝状从高压侧向低压侧逐渐发展扩大，严重时可导致高压侧部分的绝缘失效。图2为剥离伞裙护套的芯棒表面，缺陷整体呈现狭长的三角形，如同树枝般向低压侧延伸，且根据工程经验发现缺陷的跨度不大，轴向发展的速度大于横向发展的速度。因此，本文将界面缺陷假设为等腰三角形，考虑到尖端放电的影响和计算机的仿真算力，将等腰三角形的尖端改为曲率半径较小的圆弧。通过改变等腰三角形缺陷的尖端曲率半径、长度、跨度和厚度这4个尺寸参数来研究参数变化时引起的电场畸变情况。等腰三角形缺陷示意图如图3所示。

图2 剥离伞裙护套的芯棒表面Fig.2 Core rod surface with sheath stripped

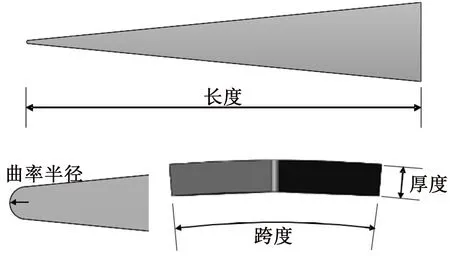
图3 等腰三角形缺陷示意图Fig.3 Diagram of isosceles triangle defect

本文根据对实际剖检故障绝缘子的观察结果，把界面缺陷设置在高压侧第4对大小伞裙之间，并假设缺陷逐渐向低压侧发展，如图4所示。

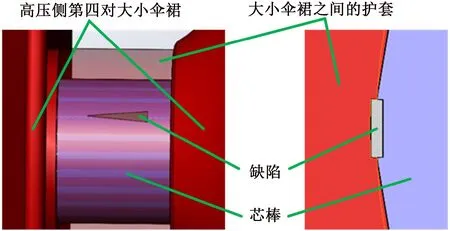
图4 界面缺陷位置示意图Fig.4 Schematic diagram of interface defect location

1.3 参数设置

水气浸入是一个缓慢变化的过程，故界面缺陷是从气隙逐渐转变为水隙。对两相复合材料的等效介电常数（εr）进行计算，常见的有Maxwell-Garnett公式、Bruggeman公式、体积加权平均公式等[17]。本文将界面缺陷的材料状态分为空气、不同比例的水气和纯水，其中不同比例的水气的等效介电常数利用体积加权平均法计算。模型中各材料参数如表2所示。

表2 模型材料参数Tab.2 Model material parameters

考虑到输电线路实际运行时存在绝缘子承受最高幅值相电压的情况，将高压侧金具电位设置为449 kV，低压侧金具电位设置为0 kV。为兼顾仿真结果的准确性和仿真过程的计算量，对于界面缺陷部位人工设置尺寸较小的网格剖分，复合绝缘子的剩余部位直接选用较细化网格剖分，空气域按常规网格剖分。

2 缺陷附近的电场分布情况

通过对等腰三角形界面缺陷进行仿真，并将其与常见的弧形柱体界面缺陷仿真结果进行对比，观察二者附近电场分布情况的差异。将两种形状的界面缺陷模型设置为相同的尺寸参数，长度为10 mm，跨度为10°，厚度为0.3 mm，其中等腰三角形缺陷的尖端曲率半径为0.01 mm。首先将二者的材料类型设置为空气，形成气隙缺陷，图5和图6分别为弧形柱体和等腰三角形界面缺陷仿真所得电场分布情况。

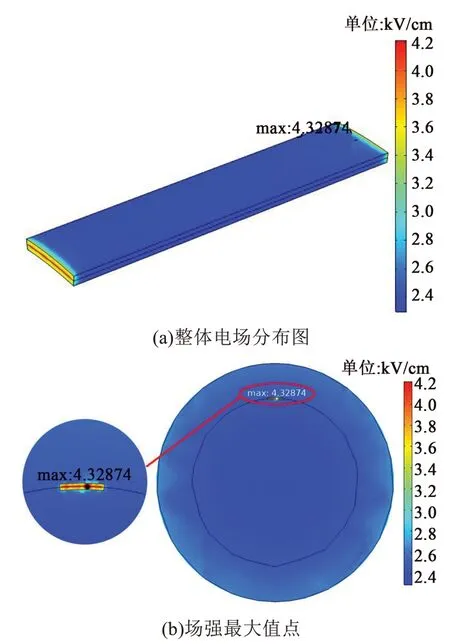
图5 弧形柱体缺陷空气状态下电场分布Fig.5 Electric field distribution of arc cylinder defect in air state

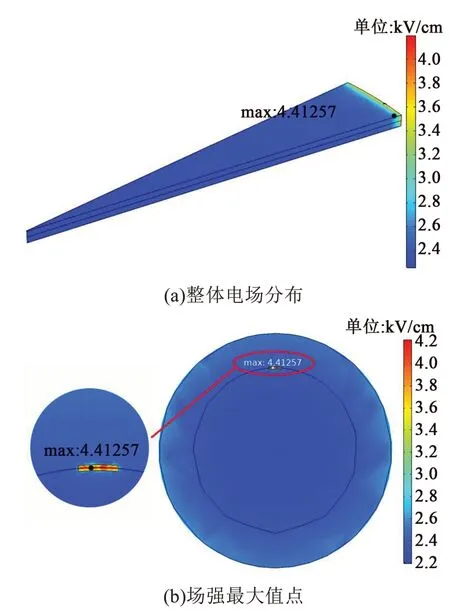
图6 等腰三角形缺陷空气状态下电场分布Fig.6 Electric field distribution of isosceles triangle defect in air state

由图5和图6可知，两种形状缺陷在空气状态下的电场强度最大值出现在高压侧与护套和芯棒的交界面上，且最大值点的位置在交界面中央。弧形柱体气隙的场强最大值约为4.329 kV/cm，等腰三角形气隙的场强最大值约为4.413 kV/cm，二者相差不大。

再将二者的材料类型设置为水，形成水隙缺陷，仿真所得电场分布情况分别如图7和图8所示。

由图7可知，弧形柱体缺陷在水状态下的电场强度最大值出现在低压侧与护套和芯棒的交界处，其位置在柱体的角上，场强约为10.621 kV/cm。从图8可以看出，等腰三角形缺陷在水状态下的电场强度最大值出现在低压侧与护套和芯棒交界的尖端部位，场强约为62.483 kV/cm，远高于弧形柱体水隙场强的仿真结果，近似弧形柱体水隙场强的6倍。

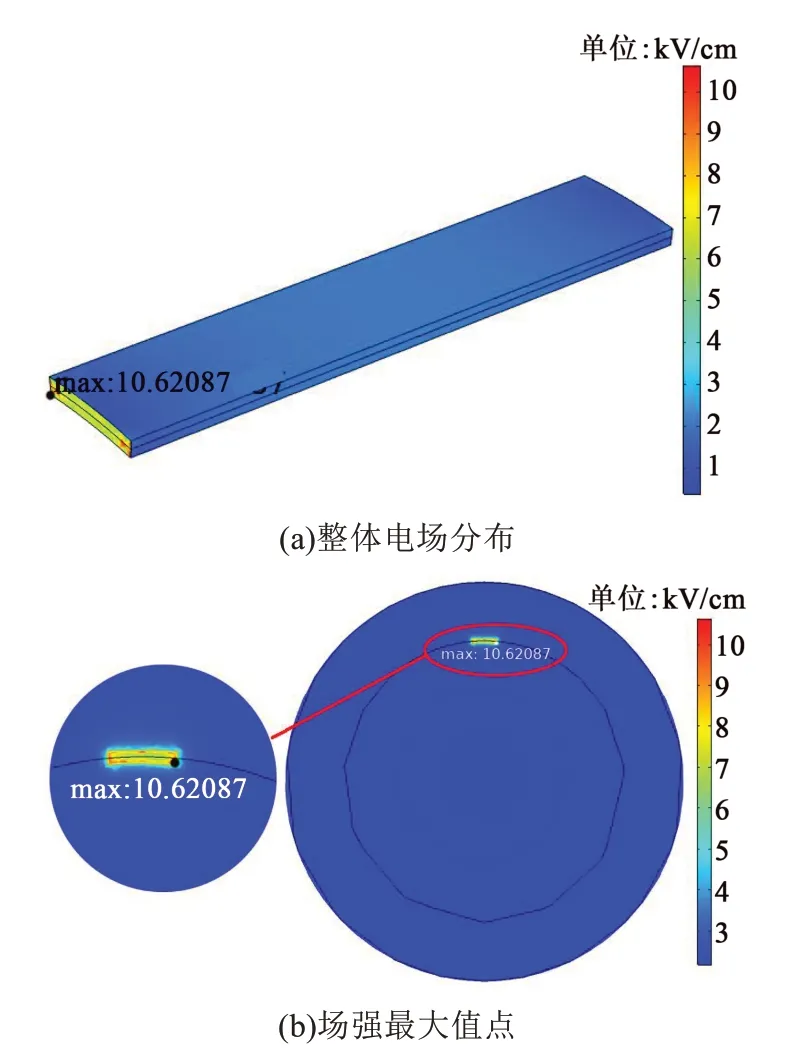
图7 弧形柱体缺陷水状态下电场分布Fig.7 Electric field distribution of arc cylinder defect in water state

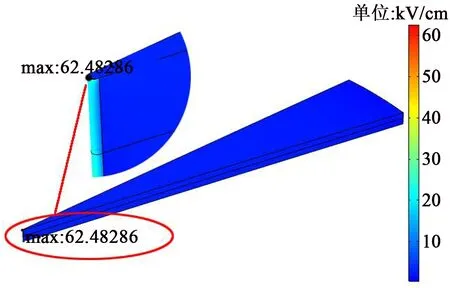
图8 等腰三角形缺陷水状态下电场分布Fig.8 Electric field distribution of isosceles triangle defect in water state

综合上述仿真结果，当界面缺陷为空气状态时，气隙的场强最大值出现在缺陷、护套、芯棒三者的交界面中央；当界面缺陷为水状态时，弧形柱体水隙的场强最大值在交界面的角上，而等腰三角形水隙的场强最大值位于尖端的角上。下面以等腰三角形缺陷的结果为例进行分析。

为便于分析，将等腰三角形缺陷视作圆锥体来建立球坐标系，圆锥体的尖端即为此坐标系的原点O，其轴即为坐标系的极轴，如图9所示。记α为圆锥体的半顶角，记θ为半顶角α的补角，则尖端部位表面的面电荷密度如式（1）所示，其附近的电场强度如式（2）～（3）所示[18]。

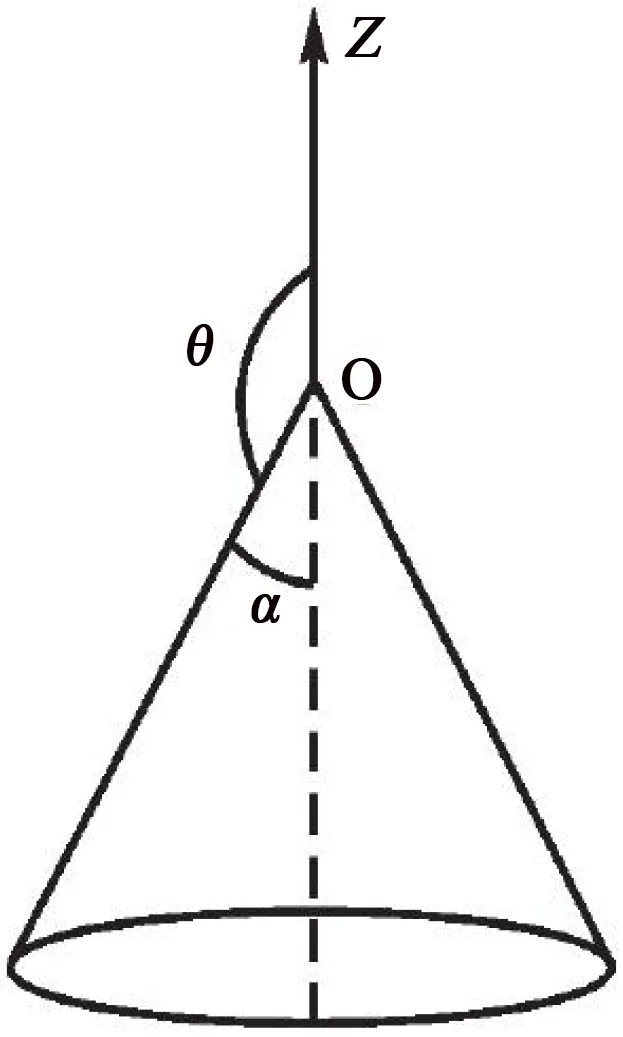
图9 圆锥体坐标系示意图Fig.9 Schematic diagram of the cone coordinate system

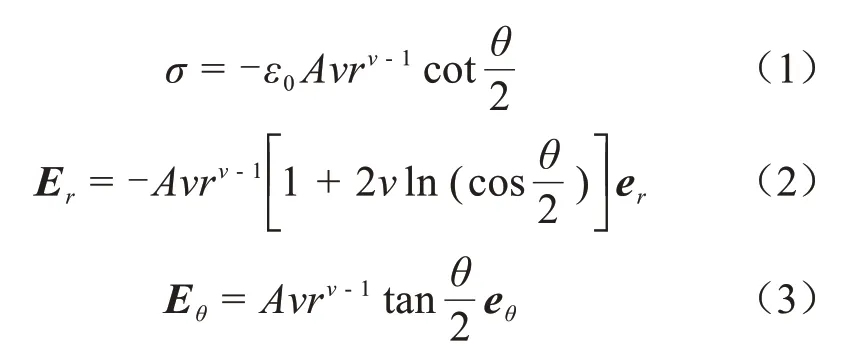
式（1）～（3）中：A为某一包围着电场存在的曲面区域，在此不作考虑；ε0为真空介电常数；r为尖端曲率半径；σ为面电荷密度；Er和Eθ是沿着r与θ方向的电场；e是电子常量；v是随着α变化的参量，其最小值公式如式（4）所示。

当α=10°时，v=0.2；当α=1°时，v=0.1；当α=0°15'时，v=0.08。因此可以推出，在α趋近于0°，θ趋近于180°时，面电荷密度α与r-1成正比。由此看出，圆锥体尖端的面电荷密度随着其曲率半径的增大而增大。当v＜1时，距离导体尖端越近，面电荷密度越大；距离导体尖端越远，其面电荷密度越小。而尖端附近的电场强度与其面电荷密度成正比，所以距离导体尖端越近，电场强度越大，反之则越小。

当等腰三角形缺陷为水隙时，水是导体且相对介电常数远大于护套和芯棒的相对介电常数，其低压侧的尖端存在尖端效应，导致其附近的电场强度最大值出现在尖端部位。当等腰三角形缺陷为气隙时，空气的相对介电常数小于护套和芯棒的相对介电常数，仅从数值大小上可以假设护套和芯棒是导体，在尖端效应的影响下，缺陷模型的几个角和尖端部位的曲率半径为负值，面电荷密度相对于平面来说非常小，因此场强最大值出现在交界面的中央而不是尖端部位。

当绝缘子的护套破损受潮时，等腰三角形缺陷内逐渐渗入水分，最终转变为水汽缺陷。其尖端的场强很大，并伴随着水分子的极化损耗发热，导致缺陷向低压侧不断发展。与弧形柱体缺陷相比，能更好地反映出缺陷向低压侧发展的方向性和趋势。

3 缺陷尺寸的影响

前人通过改变球体缺陷的半径，或弧形柱体的长度、跨度、厚度等方法来研究不同尺寸界面缺陷对电场分布的影响。本文提出的等腰三角形缺陷具有长度、跨度、厚度和尖端曲率半径这4个参数。其中，针对长度、跨度和厚度的仿真结果与前人所得结果近似，即缺陷的场强最大值与其长度呈负相关，与跨度和厚度呈正相关，而随着长度、跨度或厚度的增加，场强最大值的衰减或增长速率也有所减缓。因此本文不展开讨论，仅对尖端曲率半径这一参数进行分析。

将界面缺陷模型的长度分别设为5、10、20 mm，跨度设为30°，厚度设为0.3 mm，尖端曲率半径从0.01～0.06 mm变化，步长为0.01 mm。不同状态下场强最大值随尖端曲率半径的变化趋势如图10所示。

图10 不同状态下电场强度最大值随缺陷尖端曲率半径的变化Fig.10 The variation of maximum electric field strength of defects with the curvature radius in different states

从图10可以看出，在空气缺陷下，等腰三角形缺陷尖端曲率半径的变化对场强最大值的影响不大，而缺陷长度与场强最大值呈负相关。但在水汽缺陷下，场强最大值随着缺陷尖端曲率半径的增大而减小，且减小的趋势逐渐变缓。上文提到实际的界面缺陷呈树枝状，尖端的曲率半径可能更小，所以在水分侵入后尖端部位的电场强度将会更大，存在放电和击穿的隐患。

根据第2节的分析结果可以得到水隙场强最大值随着尖端曲率半径的减小而增大。而空气不是导体，因此尖端效应可以忽略，尖端曲率半径的变化对气隙场强最大值不会产生明显影响。

在对实际挂网运行的复合绝缘子进行巡检时发现，在具有内部界面缺陷的故障绝缘子中，已经出现的内部缺陷往往会在较短时间内迅速发展，由高压侧向中段发展。水汽缺陷在向绝缘子中段发展的过程中，呈树枝状延伸，具有尖端效应，导致尖端的场强越来越大，因此缺陷发展的速度也越来越快。

4 水气浸入过程的影响

4.1 界面缺陷对电场分布的影响

对是否存在界面缺陷的复合绝缘子整体轴向电场分布情况进行比较，以长度为10 mm、跨度为10°、厚度为0.3 mm、尖端曲率半径为0.04 mm的等腰三角形缺陷为例。空气缺陷、水隙缺陷和正常情况下的轴向电场强度曲线对比情况如图11所示。

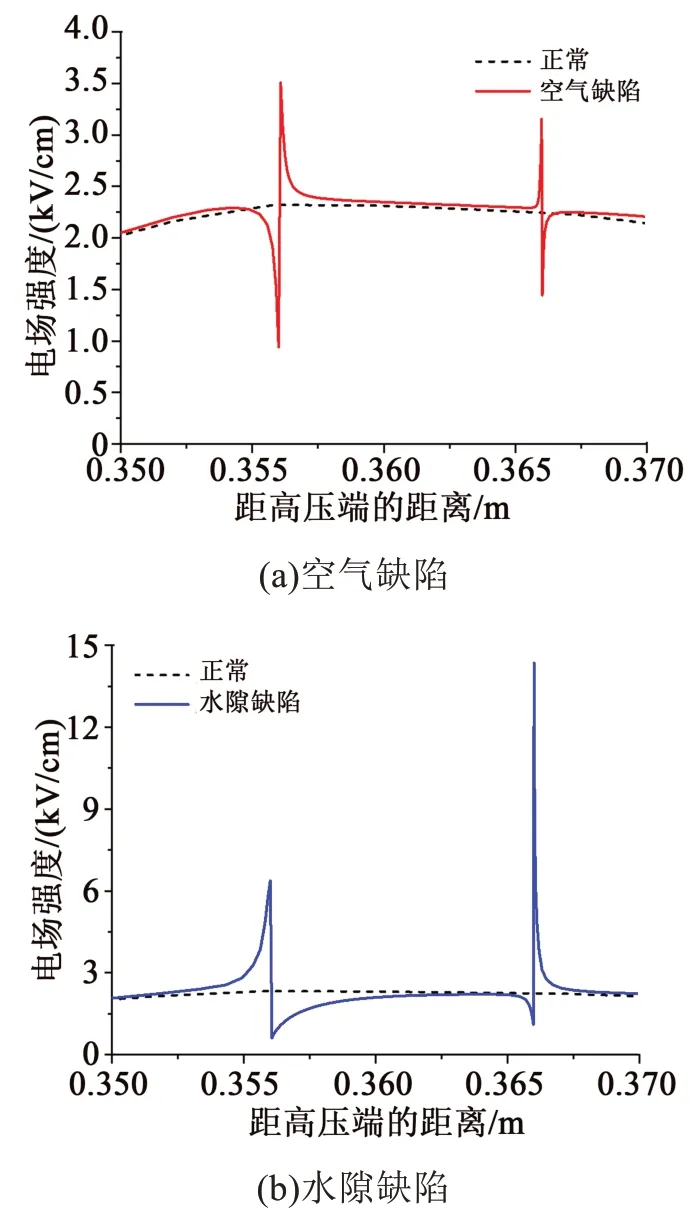
图11 不同缺陷的轴向电场强度Fig.11 Axial electric field intensity of different defects

由图11可知，当复合绝缘子的芯棒和护套交界面处出现气隙时，对绝缘子表面的轴向电场分布造成明显的影响。气隙内部的电场强度与完好状态相比有所增大，两端交界处的电场强度也显著增大。当交界面处产生水隙时，绝缘子表面的轴向电场也受到了显著的影响。水隙内部的电场强度与正常情况相比有所减小，但两端交界处的场强非常大。

4.2 不同水气比例对电场分布的影响

将界面缺陷的尖端曲率半径分别设置为0.02、0.04、0.06 mm，长度为10 mm，跨度为30°，厚度为0.3 mm，缺陷部位的材料类型设置水与空气比例分别为0∶10、2∶8、4∶6、6∶4、8∶2、10∶0，共6种状态。仿真得到6种状态下缺陷场强最大值如图12所示。由图12可知，当缺陷为空气状态时，尖端曲率半径的变化对场强最大值基本没有影响。随着缺陷中水分含量的上升，电场强度最大值逐渐增大，尖端曲率半径对场强最大值的影响逐渐显著。

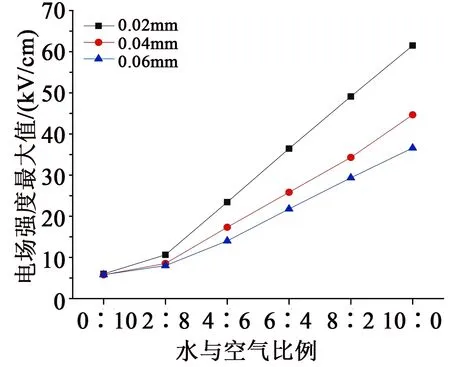
图12 不同状态下的电场强度最大值Fig.12 Maximum electric field strength indifferent dfferent states

4.3 结果分析

根据高斯通量定理对气隙存在前后绝缘子局部电场强度的变化情况进行分析，如式（5）所示。

式（5）中：D为被研究区域内的电位移矢量；S为包含被研究区域的闭合曲面；q为闭合曲面S内的总电荷量。

因本文中的缺陷部位为均匀的线性介质，故有电位移矢量公式如式（6）所示。

式（6）中：E为缺陷内部的电场强度；ε0为真空介电常数；εr为相对介电常数。

将式（6）代入式（5），得到式（7）。

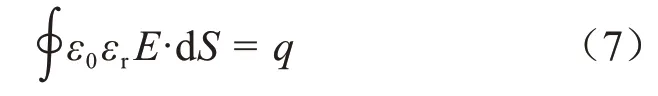
由于缺陷整体呈现电中性，其内部包含的电荷总量q不变，并且在本文中缺陷的表面积S没有改变，可以得出缺陷内部的电场强度E与相对介电常数εr呈反比关系。空气的相对介电常数小于芯棒和护套的相对介电常数，所以缺陷内部的电场强度与完好情况时的同一部位相比会增大。而随着缺陷尺寸的增大，其周围的等效相对介电常数会趋于稳定，因此电场强度的变化速率也会趋于缓慢。类似地，水的相对介电常数大于芯棒和护套的相对介电常数，所以内部的电场强度与正常情况相比有所减小。

当复合绝缘子界面缺陷因护套破损受潮渗入水分后，变为水汽缺陷。随着水分含量的上升，缺陷整体的相对介电常数增大，在尖端部位的尖端效应也会越来越明显，缺陷的尖端电场强度越来越大，其向着低压侧发展的速度也越来越快。

5 结论

（1）根据工程经验提出了一种包含尖端曲率半径尺寸参数的等腰三角形缺陷模型。等腰三角形缺陷与弧形柱体缺陷为气隙缺陷时的场强最大值均位于高压侧与护套、芯棒交界面的中央，数值差别不大。当水汽浸入后，弧形柱体水隙的场强最大值位于交界面的角上，而等腰三角形水隙的场强最大值位于尖端且数值很大，能更好地反映出缺陷向低压侧快速发展的趋势。

（2）水隙与气隙相比更易受到尖端曲率半径的影响。等腰三角形缺陷的尖端曲率半径对气隙的场强最大值几乎没有影响。但水隙的场强最大值与尖端曲率半径呈负相关，且随着尖端曲率半径的增大，其对场强的影响作用逐渐减弱。

（3）缺陷的场强最大值随着水分含量的上升而增大。因此当护套破损受潮时，水汽浸入后的缺陷更容易发生局部放电。水隙发展的过程中呈树枝状延伸，具有尖端效应，导致尖端的场强越来越大，增大了局部放电的可能性。