美国学术类博士生教育规模的周期波动

董 渊 王任模 钟晓征 韩芳明 刘丽霞

位于教育体系顶端的博士生教育，是高层次创新人才的主要培养途径，越来越多地被当作一种国家战略资源[1]。同时“一流博士生教育体现一流大学人才培养的高度”[2]，受到广泛关注和高度重视。

一、美国博士生教育规模增长规律的前期研究

21世纪以来全球主要经济体博士生教育发展迅猛[3]，而相关的发展规律研究是受到长期关注的重要话题[4]。自1861年开始授予学位[5]，美国博士生教育160多年已经发展为全球产出规模最大和竞争力最强的高层次人才培养体系，成为其国家创新能力的重要组成部分，因而也成为广为关注的研究对象，特别是作为我国教育发展研究的比较对象[6-8]。针对美国博士生教育规模，有用于在学博士生规模预测、基于完成率与流失率的时间序列模型[9]，有美国国家教育统计中心（National Center for Education Statistics，NCES）用于学位授予规模预测、基于多元线性回归的模型[10]。针对美国近百年来博士生教育规模发展规律，根据授予规模增长量变化幅度识别出1961—1973年、1988—1996年和2003—2009年等三个增长较快的时期，并发现每个较快增长期之后都有一段时间的振荡调整[11]。根据授予规模增长率变化幅度识别出美国在20世纪20年代、50年代和90年代有三个增长较快的阶段，且这种变化与其经济增长保持着同步共振[12]。博士生教育动力学模型揭示主要规模数据可以用链式反应类似的数学方程描述、符合指数变化规律，定性识别出近100年来美国学术类博士生教育发展包含5个“U”型“衰减—恢复”周期，并预测即将进入持续20—30年的新周期[13]。

美国学术类博士生教育规模发展是否存在一致的波动规律？如何定量描述？针对这些问题，本文深入研究美国学术类博士学位授予数据与其动力学模型指数规律测算数据之间偏离程度的变化规律，探索其波动特性，并探讨基于指数规律和波动特性的定量预测方法。

二、博士生教育链式反应的偏离度分析

1.博士生教育规模的指数变化规律

某一国家或地区博士生在学规模可当作年度为单位的离散时间序列，可采用以时间为自变量的连续函数来近似描述。基于博士生教育动力学模型的研究表明，在总体发展趋势保持超过十年大致不变的情况下，该函数满足链式反应类似的数学方程、符合指数变化规律[13]，可表示为：

其中：0E为初始在学规模，μ为博士生教育成长指数，表达式为：

其中年度招生比α、年度生师比ρ、年度退出率ε、年度学位获得率β分别定义为：

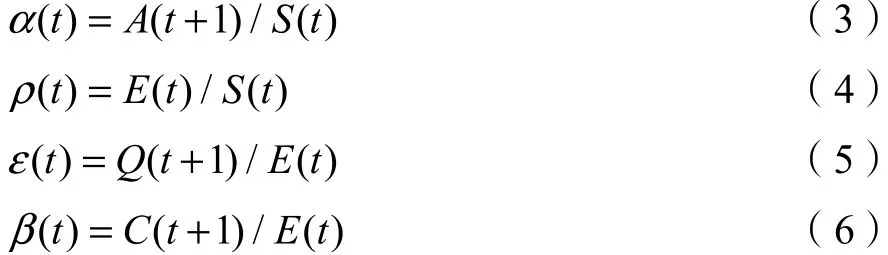
S(t)为t年指导教师规模，A(t+1)、Q(t+1)、C(t+1)分别为t+1年招生、退出和学位授予规模。通过等式（1—6）可得指导教师、招生、退出和学位授予规模的表达式，由此可知这些博士生教育相关的主要规模数据均符合指数变化规律。其中学位授予规模为：

考虑到经济、科技和教育政策相对稳定，参数μ具有较为明显的阶段性特征。为此可以采用分段滚动模型进行博士生教育相关规模数据的分析和测算，对于学位授予规模，假设分为n段，其中i= 0,1,… ,n-1，ti为各段的起始年份，则可以分段表示为：

为方便数据分析，可对相关等式两边取自然对数。分段表达式（8）两边取自然对数后为：

在以时间为横轴、求取自然对数后的规模数据为纵轴的单自然对数坐标系中，其图形近似为具有不同斜率的折线段组合，可以通过分段线性拟合进行参数估计[13]。

2.博士生教育规模数据的偏离度

定义博士生教育规模数据的成长偏离度（以下简称“偏离度”），为实际规模数据与相应指数规律基线数据（目标数据）之差所占基线数据的比重。学位授予数据的偏离度为：

其中()C t˜为学位授予实际数据，()C t为学位授予基线数据，可由拟合所得分段指数函数计算。

对博士生教育实际规模数据取自然对数，基于等式（9）通过分段线性拟合进行参数估计。以分段指数函数作为基线函数，求取实际数据和基线数据之间的偏离度，进行偏离度分布分析，有助于进一步理解博士生教育的变化规律。这里以美国学术类博士学位授予数据为例进行讨论。

NCES传统统计口径①NCES 1960—2009年使用的统计口径。其中，学术类博士含哲学博士（Ph.D.）、教育博士（Ed.D.）等，实践类博士含临床医学博士（M.D.）、法律博士（J.D.）等第一职业学位（First-Professional Degrees，FPD）。美国学术类博士授予数据②数据来源：1861—1958年数据来自American Universities and Colleges (8th Ed.), 1960。1959年数据来自Academic Degrees: Earned and Honorary Degrees Conferred by Institutions of Higher Education in the United States, 1960。1960—2020年数据来自NCES Digest of Education Statistics，其中2010—2020年学术类博士数据参照文献9方案由授予总数和传统统计口径实践类博士数据推算得到。跨年统计数据计入截止年份。分段指数拟合和单自然对数坐标下分段线性拟合结果如图1。可分为形成阶段、工业化时代和信息化时代三个发展阶段，近100年来经历一战、二战、冷战前期、冷战后期和后冷战期等5个“U”型“衰减—恢复”周期[13]。

（1）偏离度的“增长”和“衰减”。基于图1数据，以分段指数函数计算结果作为基线数据，求得美国学术类博士学位授予数据偏离度曲线如图2上半部分虚线所示。

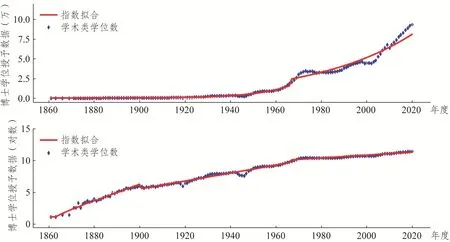
图1 美国历年学术类博士学位授予数据分段拟合

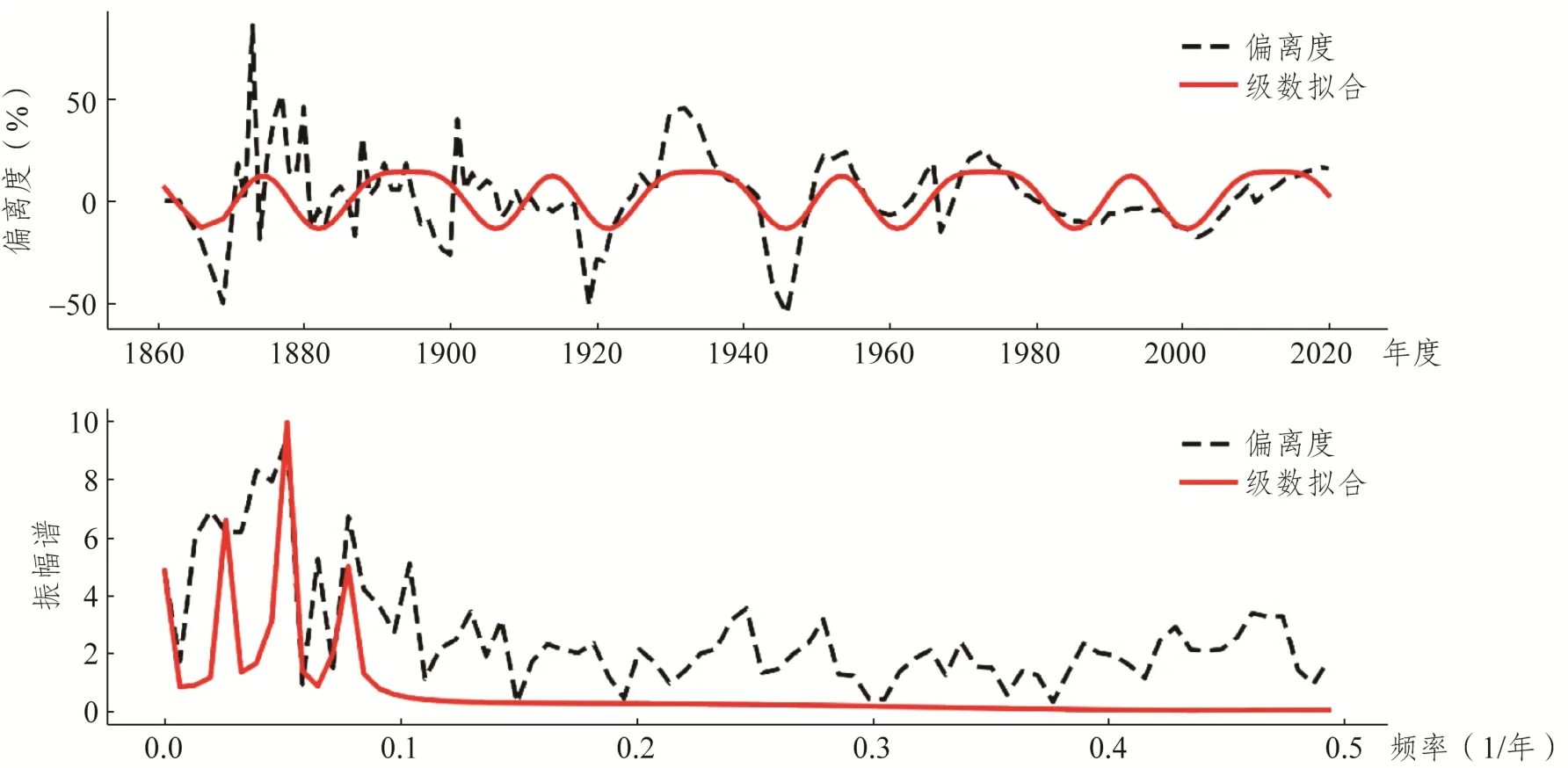
图2 美国学术类博士学位授予数据偏离度的傅里叶级数拟合

偏离度描述实际规模数据相对分段指数函数的偏离程度。偏离度为正、为负表示当年实际规模数据高于或者低于相应的指数函数在该年的数值，而偏离度增长、衰减表示偏离度数值的增减，对应着某个年份偏离度曲线一阶导数为正或为负的情况。

以美国学术类博士一战结束到二战结束1919—1946年间的波动为例来讨论偏离度增长和衰减的情况。如图1和图2上半部分所示，1919—1932年间处于增长区间，波峰、波谷之外各点偏离度导数为正，表示该时段授予规模的增长速度“跑赢”相应指数函数。其中，1919—1924年间偏离度数值为负，表示这些年份的授予规模低于相应指数函数在该年的数值，1925—1932年偏离度数值为正，表示这些年份的授予规模高于相应指数函数在该年的数值。1932—1946年间处于衰减区间，波峰、波谷之外各点偏离度导数为负，表示该时段授予规模的增长速度没有“跑赢”相应指数函数。其中，1932—1942年间偏离度数值为正，表示这些年份的授予规模高于相应指数函数在该年的数值，1943—1946年间偏离度数值为负，表示这些年份的授予规模低于相应指数函数在该年的数值。

（2）偏离度曲线的时频特性。美国学术类博士学位授予数据的偏离度曲线具有明显的波动特性，但各波动持续时间、振幅值以及波形各具特色，没有两个波动完全相同。对偏离度曲线进行离散傅里叶变换[14]，绘制振幅谱如图2下半部分虚线，振幅谱在整个区间均有分布且具有多峰特性，属于非周期信号的连续谱。其中第一个峰值位于f1≈ 0.025（1/年）、T1= 1/f1=40（年），对应基频，而最高峰位于f2= 2f1≈ 0.05（1/年）、T2= T1/2 =20（年），对应二倍频。可见，偏离度曲线不属于严格意义的周期变化，但具有明显的周期波动特性，可采用周期函数来近似描述。

（3）傅里叶级数近似。为进一步分析偏离度曲线的波动特性，参照事物从无到有、再从由弱到强、进而由盛转衰的一般发展规律，同时考虑时域偏离度曲线波峰和波谷易于识别的实际情况，采用“增长—衰减”的倒“U”型周期波动模型，以周期函数ƒ()t的余弦傅里叶级数[15]表达式来近似偏离度曲线，将“增长”起始点（谷底）对应年份作为各周期的起始年份，其表达式为：

其中a0与偏离度曲线均值有关，aj为第j阶分量的振幅，t0为与相位偏移相关的年份。考虑傅里叶级数的收敛特性，可以采用具有足够阶数的级数表达式作为偏离度曲线的近似函数。

（4）相似性判别。实际使用的关键在于选取合适的阶数，使得函数ƒ(t)与偏离度曲线具有足够的相似程度，并保持合理的计算规模。这里，将偏离度曲线DevC(t)和函数ƒ(t)的离散序列看作两个独立向量，采用余弦相似度，即两向量间夹角的余弦值，来度量二者的相似性[16]，表达为：

其中分子为两个向量的点积，分母为两个向量模的乘积。δ数值越接近1，则两个向量的相似性越强。

（5）拟合阶数。采用最小二乘法对美国学术类博士学位授予规模偏离度曲线以式（11）分别进行1—6阶余弦傅里叶级数拟合，以等式（12）计算拟合结果和偏离度曲线之间的余弦相似度，结果如表1所示。

表1 美国学术类博士学位授予数据偏离度曲线的傅里叶级数拟合情况

拟合结果中，一阶、二阶、三阶级数分量对应a1、a2、a3的绝对值较大。从余弦相似度数值来看，三阶拟合的相似度为0.52，此时拟合结果和实际数据具有中等程度的相似性。而更高阶拟合结果显示，随着拟合阶数的提高，相似度的改善不明显。从频谱分布情况看，在基频f1、二倍频f2和三倍频f3位置存在着明显峰值，表明这三个频率对应的分量为该波动的主要分量。

综合考虑，选取基频为f1的三阶傅里叶级数作为160多年来美国学术类博士学位授予数据偏离度曲线的近似表达，以开展后续分析。相应的时域和频域曲线在图2中采用实线绘制。

3.美国学术类博士学位授予数据的周期波动规律

根据学位授予数据分段表达式（8）、偏离度近似函数ƒ()t的余弦傅里叶级数表达（11）和偏离度定义（10），可知博士学位授予数据可近似为分段指数函数与余弦傅里叶级数的组合，表明美国学术类博士学位授予数据遵循具有周期波动特性的指数规律变化，可表示为：

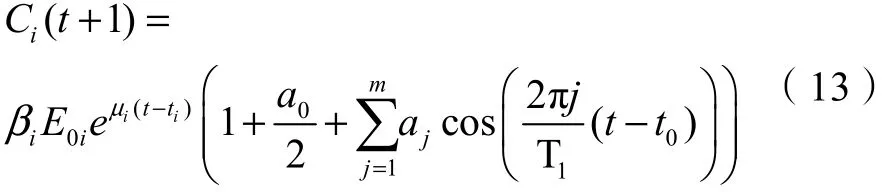
其三阶近似表达式的主体为分段指数函数，同时叠加周期约40年、20年和13年的三阶余弦函数分量，其中二倍频f2对应幅值a2的绝对值最大，因此约20年周期波动的特征更为明显，160多年来经历了8个约20年周期的倒“U”型“增长—衰减”波动。

表2给出各波动的周期T2、增长和衰减的区间、偏离度波峰（极大值，Max）和波谷（极小值，Min）等初步数据，并参照参考文献第13条中的命名策略，标出各周期衰减区间最具有影响力的重大事件。参考文献第11条中给出1961—1973年、1988—1996年和2003—2009年等三个增长较快的时期，以及各增长期之后的振荡调整，大致分别对应于本文的第6、7、8周期。参考文献第12条识别出美国在20世纪20年代、50年代和90年代有三个增长较快的阶段，则大致分别对应于本文的第4、5、7周期的增长区间。

（1）倒“U”型波动。本文采用倒“U”型波动模型，各周期以两侧波谷作为起止点、包含“增长”和“衰减”两部分。该模型可以更好地刻画美国学术类博士160年的发展历史，第一个周期的起始点位于美国学术类博士生教育的起点附近，而根据分段线性拟合结果将160年历史划分为三个成长指数逐步降低的阶段，不同阶段的边界和周期的边界相近，其中“形成阶段”含2个周期、“工业化时代”阶段含3个周期，当前正处于“信息化时代”阶段第3个周期中部。而参考文献第13条中采用的“U”型波动模型，各周期以两侧波峰作为起止点、含“衰减”和“恢复”两部分，与本文模型间有约10年的相位差，该文识别出近百年来的5个周期可对应于本文第3周期峰值到第8周期峰值之间的各波动。

（2）世界大战导致的异常数据。图2中除1880年之前授予规模较小时期出现偏离度较大的数据外，在一战、二战期间，相应有两组偏离度较大的数据。美国1917年4月到1918年11月参加一战，1941年12月到1945年8月参加二战[17]。与此对应，如图2和表2显示，1918年、1919年两年形成极小值超过50%的深谷，1943—1946年间形成另一个极小值超过55%的深谷。

表2 美国学术类博士学位授予数据周期波动情况

为进一步分析世界大战类似的重大事件对美国学术类博士学位授予规模变化的影响，将1918年、1919年，1943—1946年等6年的数据作为异常数据剔除，重新计算偏离度并以等式（11）进行级数拟合。发现剔除异常数据后美国学术类博士学位授予数据的偏离度曲线，仍可由基频为f1（对应周期T1=40年）的余弦傅里叶级数来近似刻画。与剔除异常数据之前的拟合结果相比，各阶分量的振幅有所不同，特别地，周期约为20年的二倍频对应的幅值大幅下降。

由此可知，两次世界大战造成战争期间的美国学术类博士学位授予数据急剧减少，使得相关年份的授予数据大幅下降，但偏离度的周期波动规律依然保持。

三、基于具有周期波动特性指数规律的规模预测

动力学模型给出博士生教育规模遵循指数发展规律，学位授予数据偏离度分析揭示美国学术类博士生教育规模的周期波动特性，规模可以近似表达

为分段指数函数与傅里叶级数的组合。综合上述结果，考虑博士生教育发展具有阶段性特征的实际情况，在相关参数保持不变的某个阶段内，可根据等式（13）的近似表达式外推延拓进行授予数据定量预测。以NCES发布的美国学术类博士学位授予数据为例进行预测实验，并与相应的实际数据、预测数据进行对比，以检验方法的预测能力。

1.基本步骤

（1）模型基本参数识别。首先对作为输入的历年实际授予数据求取自然对数，接着在单自然对数坐标下采用最小二乘法进行分段线性拟合，获取各阶段博士生教育成长指数。之后计算博士学位授予数据的偏离度，并采用最小二乘法对偏离度曲线进行傅里叶级数拟合，获取相应的周期参数。

（2）近似表达式拟合。将分段指数拟合得到的成长指数、偏离度拟合得到的周期参数作为初值，采用最小二乘法，对授予数据以近似表达式（13）进行函数拟合，确定该近似表达式的相关参数。

（3）延拓预测。以上述拟合所得博士生教育成长指数数值作为近似表达式中指数函数的参数，根据学位授予数据偏离度曲线的傅里叶拟合结果，结合当时形势发展，对一段时间可能的“增长”和“衰减”程度以及周期时长、振幅范围进行判定，使用近似表达式对待预测时段进行延拓计算即可得到预测值。

2.2010—2020年美国学术类博士学位授予规模预测实验

采用上述方法以1861—2009年美国学术类博士学位实际授予数据作为输入，预测2010—2020年授予数据，并与NCES发布的实际授予数据和预测数据进行比较。其中实际授予数据与前文使用数据相同，用于对比的预测数据为NCES于2010年发布的多元线性回归模型测算结果[18]。

根据上述基本步骤，对历年授予数据求取自然对数后分段线性拟合获取各阶段博士生教育成长指数，以相应的分段指数函数计算结果作为基线数据计算授予数据的偏离度，采用最小二乘法拟合得到周期函数的相关参数。将拟合得到的指数函数参数和周期参数作为初值，对授予数据以近似表达式（13）进行函数拟合，确定该近似表达式的相关参数。以相应的周期和振幅作为近似表达式中周期函数的参数，使用近似表达式对待预测时段进行延拓计算，取整到千位的预测结果及相关数据如表3。

表3 2010—2020年美国学术类博士学位授予数据预测

（1）方法可行且可信。与实际授予数据相比，本文和NCES方法预测结果的最大误差分别为-6.55%和7.49%，均方根误差分别为2.51%和4.53%。二者与实际授予数据的余弦相似度均超过0.99。本文预测结果的最大误差和均方根误差均优于NCES预测方法，表明本文方法具有良好的预测能力。

（2）成长指数估计优先。预测中，首先需要比较准确地判断近期发展趋势，包括发展阶段的划分和周期划分，并以此确定成长指数初值。实际使用中，成长指数对于数据预测结果具有决定性的影响，需要根据待预测时段在当前周期中所处的位置以及实际发展形势，综合本阶段和当前周期慎重估计。

（3）周期和振幅判定。考虑博士生教育发展具有明显的阶段性特征，即在一段时间内相关参数基本保持不变，因此当前波动的周期、振幅数值，对于预测结果数值具有直接影响，如何判定也具有很大的挑战性。一般情况下，可以简单采用拟合所得周期参数进行外推延拓，以作为参考结果。更进一步地，则需要在深入研判未来发展趋势的基础上，对衰减或者增长的时长进行预测，由此判定具体的周期数值。特别地，还需要考虑可能的影响因素，根据当前所在周期的振幅，明确待预测时段的波动幅度，并根据相关数据进行针对性的参数调整，以得到更为合理的预测数据。

3.2021—2030年美国学术类博士学位授予规模预测

应用同样的方法，以已公开的1861—2020年美国学术类博士学位实际授予数据作为输入，预测2021—2030年授予数据。“信息化时代”阶段实际授予数据和相关预测数据如图3。

图3 美国学术类博士学位授予数据预测比较

图中菱形线为历年实际授予数据，点线为NCES于2010年发布的预测结果，实线为指数拟合线，虚线为本文级数预测结果。对比历年实际授予数据与本文测算数据，二者的余弦相似度超过0.99、均方根误差为5.51%，其中2010—2020年间二者的余弦相似度超过0.99、均方根误差为2.74%。取整到千位2021—2030年授予数据预测结果如表4，同时给出取整到百位的±5%预测范围。

表4 2021—2030年美国学术类博士学位授予数据预测

（1）正在步入衰减区间。预测数据显示，在保持指数增长总体趋势的情况下，美国学术类博士学位授予规模的偏离度曲线正在进入下行通道，步入衰减区间，一段时间内授予数据增长乏力，可能无法“跑赢”相应指数函数，甚至可能出现授予规模下降的情况。

如果只关注21世纪以来美国学术类博士生教育发展，可以看到授予规模“一直在增长，只是增幅有大有小”的现象。2002—2020年间，除2010年授予数据略有下降之外，是美国历史上NCES传统统计口径下学术类博士生授予规模连续增长最长的时段，其偏离度曲线基本保持连续增长趋势。

但是放到历史大格局中审视其长期发展趋势，可以看到“波动一直存在”。正如观察授予规模增幅变化看到的那样，在一段时间的连续增长之后往往会有很长一段时间的衰减调整[11]。偏离度分析揭示的周期波动特征表明，长期增长之后紧接着是长期的衰减，比如1932—1946年间的二战周期和1973—1987年间的冷战后期周期都曾经出现连续14年的长期衰减，其中也包含着连续数年的规模下降。

从近期公布的美国博士学位授予数据来看，长期增长势头可能即将逆转的迹象已经出现。NSF SED报告显示，该口径下2020年博士授予数据为55283，较上一年的55614减少0.6%，是2017年以来规模首次出现下降，2021年的调查将考虑新冠疫情的影响[19]。NCES 2020年新统计口径下研究类（research/scholarship）博士学位授予数较上一年略有减少[20]，已经出现规模下降情况。

综合本文预测和上述事实，初步判断当前处于美国学术类博士生教育史上的第8个“增长—衰减”周期、“信息化时代”阶段的第3个周期的峰值点附近，该周期始于21世纪初，经历了二十余年的增长，可能正在步入下行通道，未来一段时间将到达谷底，之后将开启新的、美国学术类博士生教育历史上的第9个“增长—衰减”周期，预计2030年授予数接近10万。上述分析表明，未来美国学术类博士学位授予数据将经历先衰减、再增长的历程，与参考文献第13条中定性预测趋势基本一致。

本文预测方法，对于1861—2010年、1861—2020年美国学术类博士实际授予数据两组输入，给出基本一致的发展趋势预测，表明方法具有一定的稳定性。在长期增长的鼎盛期，能够根据历史发展规律预测到即将来临的衰减，也表明方法具有一定的前瞻性，有助于更早预判趋势、更好做出应对。

（2）新冠疫情影响有多大？上述预测数据基于1970—2030年间美国学术类博士生教育总体发展趋势保持大致不变（成长指数不变）且大致符合当前周期波动特征的情况下外推而得。2020年至今，新冠疫情是极为关键的全球性重大事件，是否可能造成类似一战、二战那样的异常数据呢？考虑接受博士生教育的群体主要是年轻人，世界大战直接影响参战的年轻男性，而新冠疫情对高龄和患有基础疾病群体影响更大[21]。由此推断，如果没有其他重大变化的情况下，新冠疫情可能会使得疫情严重年份的授予规模显著低于目前预测值，但应该不会像一战、二战那样造成超过50%偏离度的异常数据。

四、结论与展望

研究美国学术类博士学位授予数据与其指数模型基线数据之间的偏离程度，识别出余弦傅里叶级数形式的近似周期函数，揭示授予数据遵循具有周期波动特性的指数规律发展，并给出近似表达式，进一步推动了基于数理分析方法的博士生教育定量研究。该表达式给出美国博士生教育发展的长期发展规律，具有跨越160年历史的一致描述能力。

提出基于具有周期波动特性的指数规律、用于美国学术类博士学位授予规模的定量预测方法。数据表明，其预测略优于美国NCES基于多元线性回归模型的结果。研究认为，研究生教育规模预测误差主要源自主观因素、方法局限和政策影响[22]。本文方法基于美国学术类博士学位授予规模遵循具有周期波动特性的指数规律，适用于博士生教育主要参数保持不变的阶段，同时预测结果依赖于对未来发展形势的判断。因此，相关假设条件和发展形势的变化，国内、国际重大事件的出现，以及重要政策的调整，都可能造成预测出现偏差，应根据情况加强动态监测。

哪些因素造成美国学术类博士学位授予数据的周期波动？是经济发展周期、人口结构、产业结构变化，还是教育政策调整？相关的问题有待更为深入的探讨。周期波动特性是美国学术类博士学位授予数据的独有特性，还是各国、各学科类别博士生教育发展的普遍规律？这些都是未来可以进一步拓展的研究内容。而如何应用此类波动规律进行有针对性的规模调控，则是更有价值的话题。

更进一步地，中美全球两大主要经济体联系依然紧密的情况下，美国的博士生教育发展对于我国的博士生教育具有重要影响和参考价值。在此基础上，开展我国研究生规模演化规律探索，“发展定量与定性相结合的研究生教育学理论对于推动我国研究生教育的科学决策具有重要的现实意义”[23]，是值得长期关注的重要话题。而针对“必须增强忧患意识，更加重视人才自主培养，加快建立人才资源竞争优势”的要求[24]，进一步基于数理分析方法深入开展研究生教育研究，为推动我国博士生教育发展提出合理建议，依然是极为重要的方向。

致谢：中国学位与研究生教育学会前会长赵沁平院士关于进一步分析指数模型预测误差的指导，清华大学李京京老师关于关注全局周期特性和匿名评审专家关于定量给出各周期基本参数的建议，清华大学王传毅老师关于离散时间序列模型的指点，邵正隆老师对2020年美国学位授予数据进行的处理，都对本文工作具有重要帮助。美国博士学位授予数据收集工作得到北京航空航天大学赵世奎、美国马里兰大学李腾两位教授的帮助。在此一并感谢。