案例教学法在《离散数学》教学中的应用研究
2022-10-19孔祥艳刘自强夏晨曦李丽华
孔祥艳 刘自强 夏晨曦 李丽华
(东华理工大学 信息工程学院 江西 南昌 330013)
引言
《离散数学》是计算机专业的核心基础课程,一门课程中包含了几个数学分支内容,分别为:数理逻辑、集合论、代数系统和图论。《离散数学》课程具有定义和定理繁多、理论性强和内容抽象等特点,很容易被学生认为是一门纯数学课程,教学活动主要是教师的讲授,注重知识传授而忽略应用,更缺乏基本理论的应用与专业学科的有机结合,这使得很多学生感觉不到此课程与专业课程的关联,认为这门课程难学且没用,因而普遍对课程缺少兴趣。
虽然《离散数学》课程所教授内容以数学知识点为主,具有较强的理论性,但同时具有应用性的特点,在数据结构、程序设计、数据库、人工智能等多个领域都有较广泛的应用[1-2],因此适合使用案例教学。很多教师在《离散数学》课程中使用了案例教学方法[3-8],其中一类主要探讨案例教学的方法论,另一类则注重具体案例的设计与实施。
在国家一流本科建设专业支持下,采用了案例教学法,以期提高学生对《离散数学》课程的兴趣,加深学生对基本概念的理解,提高学生的运用知识、分析并解决工程问题的能力。
1.教学案例的设计与选取
为提高学生运用所学课程知识、分析并解决工程问题能力,既需设计与单个知识点对应的基本案例,又需设计涵盖本课程的若干个知识点和多个概念的综合性案例。在教学实践中总结出设计教学案例的4个方法:
(1)深入挖掘《离散数学》基本知识在计算机专业课程中的重要作用,这是设计好基本案例和综合案例的重要基础。图1是离散数学各知识模块与部分专业课程之间的关系图。
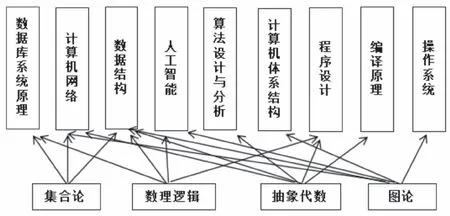
图1 离散数学各知识模块与部分专业课程之间的关系图
(2)阅读文献和国内外离散数学及其它专业课教材,并改进已有的工程案例。
(3)在各类数学建模竞赛题目中挖掘相关知识,找出实际工程中《离散数学》相关知识的应用案例。
(4)发动学生们的智慧搜集案例。让学生运用《离散数学》知识解决生活或专业课程中的一个小问题,从而深刻体会到《离散数学》知识的实用价值。
教学案例的选取非常重要,良好的课堂教学案例是实现教学目标的重要基础。如果案例选取不恰当,可能会影响教学效果。选取教学案例时需要考虑的3个重要因素如下:
(1)案例要有科学性,并与《离散数学》课程教学内容直接关联,主要使用本课程相关知识来描述和解决。
(2)案例应贴近生活或能体现离散数学知识在专业课程中的应用,以减少学生的陌生感,利于学习中的情感认同,激发学生的学习兴趣。
(3)案例中描述的问题要有挑战性,但难度适中,学生能运用离散数学的知识解决问题,从而获得成就感和信心。
2.教学案例的应用
基本案例是在教师课堂讲解单个知识点时,介绍完基本概念后引入,而综合性案例通常是在学生完成课程基本知识点及离散建模方法的学习后引入。由于本文篇幅有限,所以仅介绍几个基本案例在离散数学教学中的应用。
2.1 命题推理理论在破案时的应用
讲解完命题推理理论中几种常用论证方法和基本推理规则后,告诉学生推理理论在警察破案时也有重要的作用,并举例如下。公安人员审理某珠宝店铺金项链的失窃案,已知如下侦察结果: (1)营业员甲或乙盗窃了金项链;(2)若乙作案,则作案时间不在营业时间; (3)若甲提供的证词正确,则货柜未上锁;(4)若甲提供的证词不正确,则作案发生在营业时间;(5)货柜上了锁。问题:作案者是谁?并写出推理过程。启发学生首先将命题(1)-(5)符号化,在这过程中,如果两个命题中包含相同的原子命题,则相同的原子命题在不同的命题中使用相同的符号。通过这个例题的练习,学生们不仅复习了如何将命题符号化,学会了几种基本推理规则的灵活运用,而且认识到命题推理理论在现实生活中的重要应用价值。
2.2 笛卡尔积概念的理解及其在数据库中的应用
笛卡尔积是集合之间的一种重要运算,是一种纯数学基础理论,它为关系数据库的研究提供了重要方法,所以学生需要对笛卡尔积的概念有较深入的理解,我们通过一个案例理解笛卡尔积。例如:令A是我们班所有学生的集合,B是我们学校开设的所有课程的集合。A和B的笛卡尔积A×B是什么,A×B的子集又是什么,如何应用?启发学生可以将我们班学生只用少量学生表示,学校开始的所有课程也只用少量部分课程,从而便于用列举法表示出所求的集合。最后学生得出: 笛卡尔积A×B是由所有形如<a, b>的序偶的集合,其中a是我们班的学生而b是我们学校开设的一门课程。A×B集合表示我们班学生选课的所有可能情况,而A×B的子集表示一种可能的选课情况。学生通过做这个例题能够对笛卡尔积的概念有较形象的掌握。
接着讨论笛卡儿积在寻找连续日期中残缺的数据时的应用。例如:有个考勤记录表,记录着500个人的2022年4月的考勤信息,理论上这些人应该每天都有记录的,但可能有某些人缺少一些天的考勤数据,怎样查找出哪些人在哪些天缺少考勤记录呢?不论是按天查询和还是按人查询都比较麻烦。这种情况下,可以对这500个人的集合和2022年4月每一天得到的日期集合做笛卡尔积运算,然后与实际的表去关联,就能容易查询出结果了。通过解决寻找连续日期中残缺数据的实际问题让学生感受到笛卡尔积这个概念的实用价值。
2.3 邻接矩阵在数据结构中的应用
邻接矩阵是图论部分的一个重要概念,它是指用一个方阵表示图的各顶点之间的邻接关系,讲解完基本概念后介绍邻接矩阵一个重要应用。图的结构比较复杂,任意两个顶点之间都可能有关系,导致简单的顺序存储不能表示图,但可以借助二维数组(即邻接矩阵)来表示元素之间的关系。给出无向图、有向图和有权图这三种不同图的邻接矩阵,让学生总结出不同图的邻接矩阵分别有什么特点,从而对邻接矩阵的概念有更形象和深入的理解。告诉学生只有当图中有许多边,即图是稠密图时,用邻接矩阵表示图便于执行图的算法,但是当图包含的边较少时,用邻接表比邻接矩阵更适合,并从算法复杂度方面简单举例分析说明。
2.4 可达性矩阵在电话线路故障影响中的应用
可达性矩阵描述了图中任意两个结点间是否存在一条路及任意结点上是否存在回路,讲解完基本概念和可达性矩阵的求法后,让学生解决下列问题:设A、B、C、D、E、F六个城市之间有通信网络,并给出这些城市间的通信网络图,它们之间均可进行通话联络。某一天B和C间的线路产生故障,分析此故障对六城市间通话的影响;某一天D和F的线路产生故障,也分析此故障的影响。首先引导学生们通过题意理解以下事实:城市X与Y间可通话,若城市Y与Z间可通话,则X与Z间可通话。通过教师的启发,学生们认识到两个城市之间通过一条或多条线路相连,则它们之间就可以通话联络。然后引导他们通过分别求不同故障状态下相应图的可达性矩阵,即可解决问题。通过对此问题的解决,学生感受到可达性矩阵在解决其它领域工程问题中有重要应用价值。
结语
将案例教学法应用于《离散数学》课程教学后,学生们明显感受到此课程与专业课程的关联性较强,认为这门课程不仅在现实生活中还是在其它专业课程的学习中都很有用,从而对课程内容逐渐产生了学习兴趣。同时,学生们通过积极参与课堂互动活动并完成案例收集相关作业,大大提高了运用知识、分析并解决工程问题的能力。
