部分线性可加模型在GDP预测中的应用

□文/郑婉迪

（安徽建筑大学数理学院 安徽·合肥）

[提要］在全球经济快速发展进程中，我国作为东方大国为全球经济增长贡献巨大的力量，努力发展自身的同时也带动着周边国家的经济增长。经济活跃的直接体现是人均生产总值的不断增加，探究我国人均生产总值的主要影响因素对稳步提高居民生产消费水平具有重要意义。本文选取我国2020年31个省市地区人均生产总值进行建模预测。先对数据进行预处理，参考历史相关文献筛选出8个指标建立多元线性模型，得出粗略的预测结果。为改进预测效果，再使用Lasso变量选择方法筛选出主要影响变量，根据变量间线性相关显著性挑选出线性和非线性影响因素，继而建立半参数部分线性可加模型进行预测，该模型提高预测精度与稳健性，使回归结果在很大程度上得到优化。

从经济角度看，一个国家GDP的波动直接反映了该国家的经济发展状况变化。GDP大幅增长，说明该国经济发展蓬勃、国民收入增加，消费能力自然也随之增强；若GDP下降，则代表经济发展受损，应引起相关人员的高度关注以便及时调控。2020年爆发的新冠肺炎疫情，各国感染病例爆发式增长。为了人民的健康，党中央及时部署，采取大范围封闭管理政策，疫情得到控制的间接影响就是经济活力下降，人均收入和支出下滑。此时，研究GDP问题更有助于了解人民的收入、国家的收入和经济的健康发展情况，同时有助于维持社会的稳定等。针对这一话题的研究国内学者们多数集中在定性分析或使用传统的统计回归模型进行定量分析。王小鲁等人从政策制度方面分析了人均生产总值的影响因素和调控措施。曹海波使用因子分析的方法对影响经济增长的因素进行研究。传统的统计模型需要提前设定回归模型的形式，对数据的限制较大。影响GDP的因素多且复杂，采用OLS方法建立传统的回归模型必然导致多重共线性的出现，因此本文采用Lasso方法筛选主要的影响变量，针对此问题建立半参数部分可加模型。Lasso方法是当下比较流行的数据降维方法，虽然相比于最小二乘估计（OLS）方法对参数的估计是有偏的，但能够在保证数据相关性的同时精简变量，对处理高维数据十分有效。半参数部分线性可加模型是一种参数和非参数的组合模型，集两种模型的优点于一身，现已具有非常广泛的应用范围。

一、多元线性回归模型

变量间的非函数关系我们常称为相关关系，若它们之间存在因果关系，则可以进行回归分析。在具有因果关系的变量间建立模型进行预测也即多元回归。变量之间的线性关系在数学上是指二者存在一次函数的关系。一般的多元线性回归模型如下：

其中，Y为因变量，X1，X2，…，Xp为自变量，（Yi；Xi1，…，Xip）（i=1，2，…，n）是Y与X1，X2，…，Xp的n组观测数据，β0，β1，…，βp为未知的常值参数，εi为不可观测的随机误差项，满足E（εi）=0，Var（εi）=σ2＞0，cov（εi，εj）=0，i≠j。这种模型在以往的定量分析中是最基础的模型，也是采用最多的模型。接下来本文就建立该模型作为对比的基础。

（一）模型构建。考虑到数据的可得性和完整性，本文研究的样本空间单元为全国31个省市地区，数据来源于2021年《中国统计年鉴》。由于影响人均GDP的变量较多，为了尽可能地包含这些因素，参考国内现有的文献并结合目前的经济市场，本文选取了就业率（%）、人均第一产业生产额（元）、人均第三产业生产额（元）、城镇人口比重（%）、人均消费支出（元）、工业化程度（%）、人均进出口总额（元/人）和人均电力消费量（千瓦/时）为自变量，按序记为x1，x2，…，x8，人均生产总值（元）为因变量，建立如下多元线性回归模型并进行预测：

利用R语言中OLS对上式进行求解，拟合结果显示，虽然模型的R2a高达0.9354，R2a为自由度调整的复决定系数，但是多个变量的P值大于0.05，并不能通过检验。这粗略地说明自变量与因变量之间可能不是线性关系，也有可能是各自变量之间存在高度的相关关系，这将导致模型的稳定性非常低。

（二）模型预测。用上述模型对数据进行预测，结果如表2中模型1对应数值。根据表中数据分析，整个模型的预测精度较高，但是由于文中仅使用了一年数据进行建模，模型的稳定性并不能保证。结合多元线性的拟合结果，各自变量中仅有人均第三生产总额的p值比较显著，可以达到建模要求，而模型中选择的其他变量或多或少会对因变量产生影响，却不能通过检验，而且对于经济问题的多重共线性也不能很好地解决。因此，直接用OLS方法估计的结果是不可靠的。

表2 模型预测结果对比一览表

二、部分线性可加模型

选择与研究对象相适应的统计模型是建立模型的第一步。当下常见的统计模型主要包括参数、非参数和半参数这三大类。参数模型具有结构简单便于理解、估计结果容易解释等优点，但同时也存在许多缺点，比如模型设定严格且不灵活。非参数模型仅含未知函数，具有灵活性强的优点。但非参数模型也有着致命的不足：一是容易出现高维灾难的现象，即当解释变量X维度过高时，为使得估计精度在相对准确的范围内，在数据收集和计算时，所需数据量都不切实际地大；二是不能用于预测；三是当X的维数大于2时，估计的结果无法很好解释。第三种模型是依据前两种模型的优点组合出的模型，是含有已知的函数部分和未知参数形式的模型。此模型通过未知函数来减少模型预测偏差，加大适应性，通过未知参数来降低维度。部分线性、部分线性变系数、部分函数线性、部分函数部分线性以及部分线性可加性等五种模型均是比较常见的半参数回归模型。在这些模型中比较有代表性的是部分线性可加模型，它在减少模型偏差的同时，还能有效避免“维数祸根”。本文所采用的正是这种模型。一般的部分线性可加模型，模型形式如下：

其中，Y是因变量，X=（U，T）是d维解释变量。满足E（ε|U，T）=0，Var（Y|U，T）=Var（ε|U，T）=σ2（U，T）。

（一）Lasso变量筛选。进行统计建模的第一步便是选择合适的自变量，这一步做好了，建立的模型才能准确反映自变量与因变量之间的关系。尤其是在经济问题中自变量个数很多时，彼此之间很容易存在多重共线性，不对变量进行筛选，回归系数的估计值就会产生较大偏差，直接影响就是预测不够准确。此外，变量选择还可以剔除掉与因变量关系不大的变量，减少自变量的个数即降低模型的维度，达到精简模型的目的。本文采用Lasso这种基于惩罚函数的方法对人均GDP影响因素的变量进行筛选。Lasso变量筛选理论于1996年被Robert Tibshirani提出。但由于技术限制，在2005年才被接受应用。它和岭回归类似，都是通过构造一个惩罚函数来压缩一些回归系数，是将L2范数改为L1范数。虽然这种方法是有偏估计，但在处理具有共线性的数据时优点颇多。

设样本是（xij；yi），i=1，2，…，N，j=1，2，…，p，其中xij（xi1，…，xip）T是解释变量，yi是被解释变量。

相对于普通最小二乘估计（OLS），Lasso回归不仅简化了模型的变量，还降低了估计的方差。当样本量不足而变量却是高维时，采用最小二乘法就不合适。而Lasso对于参数的估计具有连续性，因此有必要采用Lasso做变量筛选，它可以筛选出对被解释变量影响较大的变量从而降低维度。本文采用LARS算法和CV选择参数，用R语言中的lar函数进行筛选，得到Lasso筛选结果。Lasso从所有变量中筛选出x3（人均第三产业生产额）、x5（人均消费支出）、x7（人均进出口总额）三个变量，其他的变量则被压缩至0。这就说明人均第三产业生产额、人均消费支出和人均进出口总额主要影响着人均生产总值的变化。变量筛选完毕，接下来建立部分线性可加模型。

（二）模型构建。在均方误差最小时，Lasso筛选出人均第三产业生产额、人均消费支出、人均进出口总额三个变量，基于上文建立线性模型时，人均第三产业生产额是唯一显著的线性变量，所以把这一变量作为部分线性可加模型中的线性部分，而人均消费支出和人均进出口总额则作为模型中的非线性部分，最终建立如下部分线性可加模型：

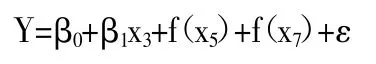
用R语言对上式进行求解，参数拟合结果如表1所示。（表1）

由表1可以看出，人均第三产业生产额的回归系数β1=1.861，经济解释就是人均第三产业生产额每增加一个单位，人均国内生产总值平均增加1.861个单位，且人均第三产业生产额的系数p-值远小于0.05，说明人均第三产业生产额通过了检验，是非常显著的。非线性部分的拟合不易解释，但从拟合过程可以大略地看出，人均消费支出在10，000～20，000元之间时，对人均生产总值的影响基本是不变的，这也比较符合我国当前的消费水平；当人均消费支出继续增加时，对人均生产总值的影响开始变小。而人均进出口总额的增加则会导致其对人均生产总值的影响变大，这也间接反映出闭关锁国只会落后的历史经验，即使在疫情之下，我们也要尽量保持在安全的情况下刺激进出口交易。综上，可以将半参数回归模型确立为：

表1 部分线性可加模型线性参数估计及模型拟合效果一览表

下面通过计算模型的拟合优度来判断该模型拟合的好坏。通过计算可得模型的拟合优度R2=0.9996，R2a也达到了0.9975。可以看出，部分线性可加模型较上文多元线性模型的拟合效果有很大提升，而且所涉及的变量只包含人均第三产业生产额、人均消费支出、人均进出口总额三个变量，整体也更加精简，这将会为我们的预测省下很多不必要数据收集的时间。

三、结论与讨论

（一）模型预测结果。将真实数据代入预测模型，经计算，预测结果如表2模型2中对应数值。（表2）

和多元线性回归模型的预测结果进行对比发现，用部分线性可加模型建立的预测更加贴合实际数据，而且模型涉及的变量更少。

（二）讨论分析。由表2可以非常直观地看出，多元线性回归模型在云南、西藏、甘肃、四川等藏区的估计偏差过大。改革开放后，藏区人民的生活已经发生了翻天覆地的变化，网络和物流的发展让当地人民的农产品和特色食品传入全国甚至全球，旅游业更是在很大程度上对当地的经济进行刺激，人均进出口总额和人均第三产业总额对这些地区的影响更大，因此这些变量对人均生产总值的影响程度并不是固定的。相对来说，半参数部分线性可加模型在这些地区的估计值更贴合实际。半参数部分线性可加模型型对人均GDP的拟合值很明显比多元线性模更加贴近真实值，说明半参数部分线性可加模型对人均GDP拟合的效果更好，而且涉及的变量也比多元线性回归模型少得多，解释起来更加具有针对性和合理性，涉及变量少，投入此项工作的时间精力消耗都会大大减少。如果政府相关部门想要对当下的经济进行调控，可以主要从第三产业和进出口方面着手。当下人民生活水平日渐提高，第三产业已经占据产业结构中的主导地位。同时，加强进出口消费，倡导全球经济一体化已经多年，我们也享受到全球化的红利，接下来更要践行这一伟大倡议，迎合全球发展趋势，带动自身的发展。