基于分数阶灰色模型的中国天然气消费量预测

王辉,陈玉珍,董瑞

（河南科技学院数学科学学院,河南 新乡 453003）

自改革开放以来,中国经济迎来了高增长与快发展时期,国民生活水平显著提高,能源消耗与日俱增.目前中国已成长为世界第二大能源消费国,消费水平在不断攀升的同时,也带来了一系列能源短缺问题和环境安全问题.近年来,这些问题已经成为了制约中国经济可持续发展的壁障,加快能源结构转型,建立节约型、高效能的产业体系已成为国家重点能源规划方向.而在化石燃料中的天然气,作为一个清洁环保型的优质燃料,在我国进行“碳达峰”和“碳中和”的过程中则能够起到关键性作用,是其他化石燃料的优质替代品之一.因此,国家在“十四五”规划中也提到了我国要继续深化能源体制改革,加快新型用能的基础设施建设[1].而天然气作为一种新型用能的代表,其消耗量必然会随之增加.科学有效地预测我国天然气消费量,有助于政府、企业做好规划,降低能源采购和配置成本.

到目前为止,学者研究天然气常用的预测方法主要分为经济统计模型、灰色模型和智能算法三类.传统的经济统计模型分为回归模型、自回归模型以及一般线性模型和广义线性模型.经济统计模型主要以时间序列法为主,根据被预测事物随时间变化的情况,推断其随时间变化的规律,进行定量预测,在能源预测上被广泛应用[2].但统计模型需要长期数据积累,对于短期的天然气消费量,数据样本量较少,无法准确推断数据变化规律,预测精度不理想.智能算法主要包括麻雀搜索算法、人工神经网络、粒子群算法、模拟退火算法以及一些组合算法[3].智能算法在解决最优化问题时大有用武之地,但缺点是只有进行大量的数据运算,才能找到全局最优解,以此来达到良好的预测精度.灰色系统则是把系统中的随机元素做为灰色数据进行处理,来挖掘内部数据规律,且灰色模型对数据样本量要求较少,不需要像其他预测方法一样需要通过大量且规律性强的数据来进行数据训练.因此对于短期的中国天然气消费量,运用灰色系统来进行预测分析可以得到更为准确的结果[4-6].

GM（1,1）模型作为灰色系统中最基础的预测模型[7-12],通过一阶数据累加,建立时间响应函数,数据累减还原等三个步骤,完成对已知信息的生成、挖掘,提取有价值的信息,实现对其未来变化的定量预测.由矩阵扰动理论可知,当累加阶数越大时,解的扰动性越大,而在扰动相等的情况下,数据量较小时,解的扰动性也越小.采用分数阶累加方法时,更满足灰色系统适合于“小数据”建模的特征.通过选用分数阶的累加方式[13-16],来改善原始数据的微小误差对模型参数的辨识度,进而提高模型的预测精度,实现模型的自适应改进.基于此,本文以中国2014-2020年天然气消费量做为原始数据,构建了灰色GM（1,1）模型、DGM（1,1）模型以及FGM（1,1）模型,并对三种模型的拟合结果进行对比分析,结果显示FGM（1,1）模型的拟合效果最好,更适合对我国天然气消费量进行预测研究.

1 数学模型

1.1 模型

背景值 z(1)(k )可表示为：z

定义2：称

为GM（1,1）模型的均值形式,而

则为GM（1,1）模型的白化方程.式（3）中,a为发展系数,b为灰色作用量.

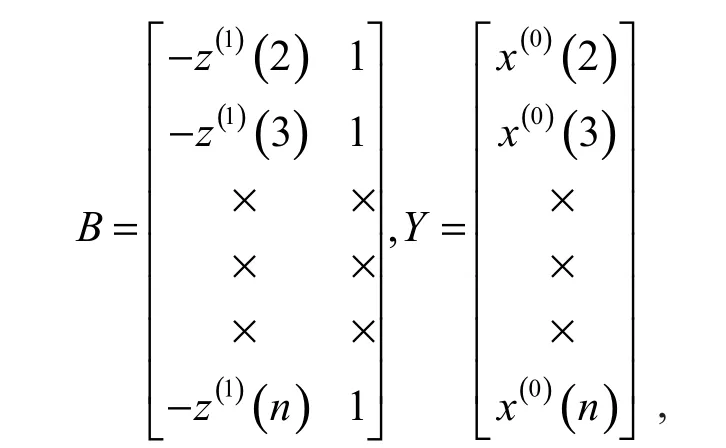
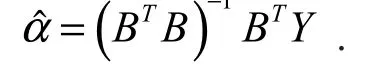
GM（1,1）模型的时间响应序列为

进一步求出累减还原式

2.2 分数阶GM（1,1）（简称为FGM（1,1））模型

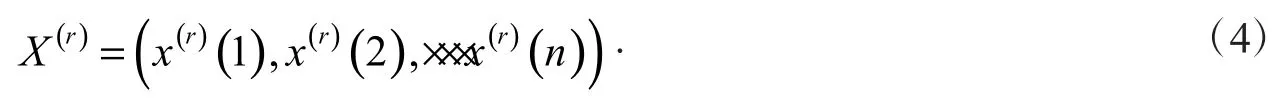
背景值 z(r)(k)可表示为

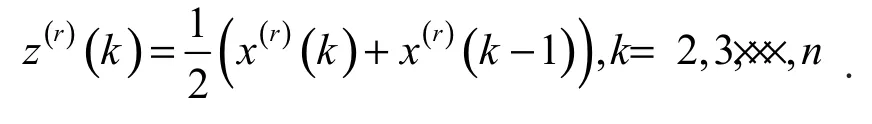
定义4：称

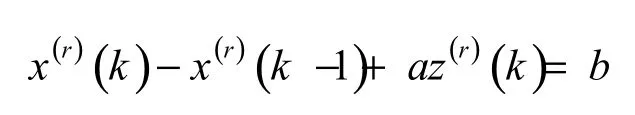
为FGM（1,1）模型的基本形式.而

为FGM（1,1）模型的白化方程.式（6）中,a 为发展系数,b为灰色作用量.

FGM（1,1）模型的灰色微分方程 x(0)(k ) + az(r)(k )=b的时间响应序列为

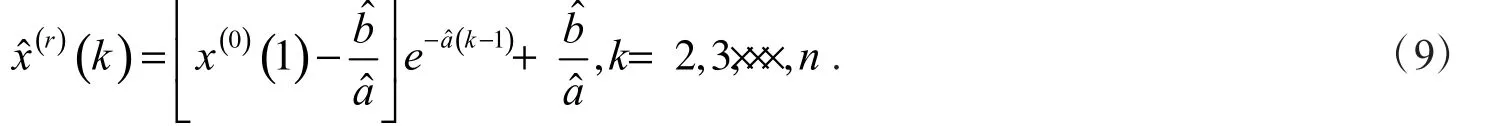
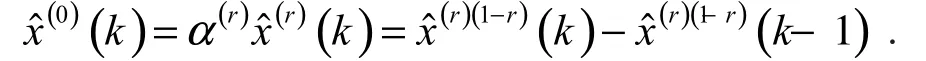
2.3 粒子群优化算法

对于灰色分数阶预测模型,不同的累加阶数会对最终的预测精度产生不同的结果,因此寻找最优阶数尤为重要.然而,传统的优化方法很难找到最优阶数.本文采用的粒子群优化算法很好地解决了这一问题[17-19].以平均相对误差最小为目标,粒子群算法适应度函数构造为

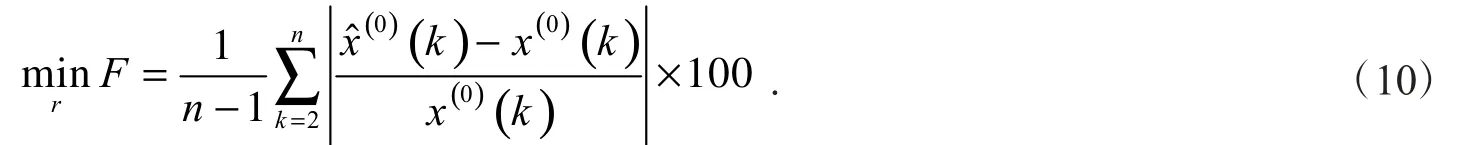
式（10）中：n为原始数据序列的数据个数.F越小,说明阶数r用于灰色建模的适应性越好.求解粒子群算法的简要数学描述如下：

假设在D维目标搜索空间中有m个粒子,将每个粒子的位置作为每个势解,第i个粒子的速度向量是位置向量是单个粒子通过的最佳位置表示为Pbest,整个粒子群经过的最佳位置表示为gbest.然后在每次迭代中,粒子速度的变化表示为

式（11）中：w是惯性矢量,r1,r2是范围内变化的随机数,Vi+1是更新粒子的速度,c1,c2是加速度常数,通常c1=c2=2,r1,r2一般是介于[0,1]的随机数.每个粒子的更新位置由速度矢量加上位置矢量确定,公式为

式（12）中：xi+1则为更新后的粒子位置.粒子通过不断地学习更新,最终飞至解空间中最优解的位置,搜索过程结束,最后输出的 gbest就是全局最优解.

为了直观方便地理解模型过程,基于粒子群优化算法的分数阶灰色预测模型的流程如图1所示.

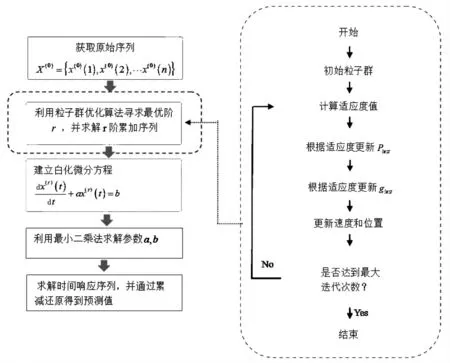
图1 基于粒子群算法的分数阶灰色预测模型流程Fig.1 Flowchart of fractional order grey prediction model based on particle swarm optimization algorithm

2.4 模型误差检验准则

为了评估所提模型的有效性,我们选择了两个标准来评估所提模型.它们分别是绝对百分比误差（APE）、平均绝对百分比误差（MAPE）.相应的计算公式如下

式（13）和（14）中：x(0)(k )代表原始值,代表预测值.预测精度也可以“分级”,以MAPE为例,其等级标准如表1所示.

表1 使用MAPE标准评估精度Tab.1 Assessing accuracy using the MAPE criterion

2 实证研究和结果分析

本文选取2014—2020年的中国天然气消费量（单位：万吨标准煤,数据来源于中国统计年鉴[20]）,建立基于粒子群算法的分数阶FGM（1,1）模型来进行运算处理.具体运算过程如下所示：

（1）选取2014—2020年中国天然气消费量作为原始数据,记为

（2）利用粒子群优化算法进行全局搜寻最优解,得到阶数为 r=0.2时是最优解,由此可知阶累加序列为

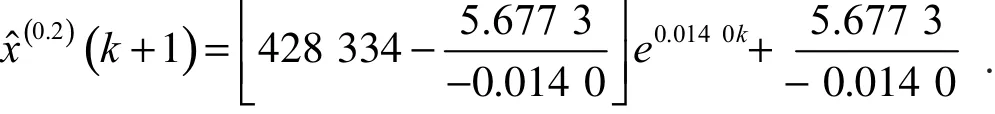
对应序列如下

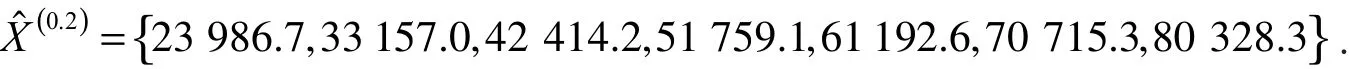
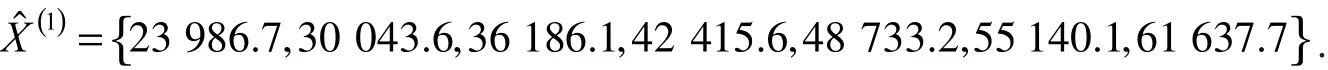
为了验证所提模型的有效性,选取GM（1,1）模型和DGM（1,1）模型来进行对比分析,拟合效果如表2所示,误差精度如图2所示.

表2 中国天然气消费量的不同灰色模型预测表现Tab.2 Prediction performance of different grey models for Natural gas consumption in China

图2 不同模型的误差精度比较图Fig.2 Comparison diagram of error accuracy of different models

通过观察表2结果可知,在粒子群算法优化下发现当阶数r=0.2时,模型的拟合值最贴近于真实值,其预测精度最高.当阶数r=1时,分数阶FGM（1,1）模型就是传统的GM（1,1）模型,其预测精度明显低于FGM（1,1）模型.因此,对于实际应用而言,寻找最优的累加算子则是提高模型的拟合效果和预测精度的一个重要方向.而通过观察图3我们能够清晰明了地感受到分数阶FGM（1,1）模型的拟合曲线更贴近于真实值,曲线走势更满足于新信息优先的原则,其预测精度也更优于传统的GM（1,1）模型和DGM（1,1）模型,在提高模型的预测精度上具有一定的现实意义.通过计算模型的平均相对误差为1.50%满足其检验准则,因此可以用来作为中国天然气消费量的预测模型.

图3 中国天然气消费量灰色预测序列图Fig.3 Grey forecast sequence diagram of Natural gas consumption in China

3 中国天然气消费量预测

本文在预测中国天然气消费量中,误差检验标准APE和MAPE均满足预测精度标准,故模型检验合格.且本文所选模型拟合效果要优于传统的GM（1,1）模型和DGM（1,1）模型.利用2014—2020年的数据来使用分数阶FGM（1,1）模型进行建模运算,得到了2021—2023年中国天然气消费量的预测值.

表3 2021—2023年中国天然气消费量预测值Tab.3 China's natural gas consumption forecast in 2021~2023

预测结果显示未来中国天然气消费量还会逐年递增,但增速呈现放缓趋势.这样的结果也完全符合我国“十四五规划”中对天然气等清洁能源的战略定位,可以为政府、企业提供一定的参考价值.

4 小结

本文通过对比传统的GM（1,1）模型、DGM（1,1）模型和分数阶FGM（1,1）模型,结果显示分数阶FGM（1,1）模型可以更好的预测中国的天然气消费量.在某些实际应用领域中,分数阶FGM（1,1）模型的拟合效果和预测精度要优于传统的GM（1,1）模型和DGM（1,1）模型.根据预测结果可知,未来几年中国天然气的消费量还会逐年递增,因此政府可考虑在工业生产、交通运输、发电等多领域有序增加天然气使用规模,将气电调峰成为以新能源为主体的新电力系统的关键部分,从而助力能源碳达峰,形成清洁低碳、安全高效的能源系统.