时间依赖路网中限制到达时间的k近邻查询

安云哲,倪灿灿,李佳佳,张安珍,夏秀峰

（沈阳航空航天大学计算机学院,辽宁 沈阳 110136）

随着配备GPS的智能设备的激增,类似于滴滴出行、Uber等平台已经成为用户必不可少的出行工具,与传统的系统相比,此类设备在减少出租车空车时间和乘客等待时间方面有了显著的进步.同时,它们也促进了路网中大量基于位置查询的研究,其中,k近邻（k-Nearest Neighbor,kNN）查询作为一种技术支持,在此类设备中发挥了重要的作用.kNN查询问题目前在静态路网和时间依赖路网中都有着广泛的研究,但是由于与本文的问题定义不同等原因,无法直接用于本文中提出的问题.

首先,静态路网中针对kNN查询的研究已经非常成熟,例如INE[1]（增量网络扩展）、IER[1]（增量欧几里得约束）、ROAD[2]、和G-tree[3]等,在静态路网中,边的权值是固定不变的,只能通过两点之间路网距离的远近来表示代价的大小.然而,在实际生活中,路网的权值是随着时间的变化而变化的,影响权值的因素有交通堵塞、天气变化等,在同一天中,同一条边的权值会发生多次改变,所以,路网中边的权值应该是一条随着时间变化的分段线性函数,仅通过距离的远近并不能反映路网中的真实代价.所以针对这一问题,本文提出了时间依赖路网中的k近邻查询,不再用距离的远近来衡量查询对象到达查询点的代价,而是使用在时间依赖路网中的实际通行时间来表示该代价.

其次,传统的kNN查询的方向是从查询点到移动对象,以查询点为中心逐步向外扩展,直到获得k个时间代价最小的移动对象,如Dijkstra算法[4].而本文关注的是查询点保持不动,从移动对象到查询点的查询,与传统查询方向相反.在静态路网中,边的权值是不变的,所以解决查询方向相反的问题,可以将路网进行反转,即将路网中所有有向边的权值设为其对应反向边的权值.通过在反向图中进行扩展,就可以得到从移动对象到查询点的代价,进而选择代价更小的移动对象作为返回结果.但是在时间依赖路网中,点和点之间的代价是一个与时间相关的线性函数,边的时间代价与出发时间有关,并且对于同一条边,在同样的查询时间,两个方向的时间代价也不同,所以无法通过简单的反转来进行从移动对象到查询点方向的kNN查询.针对这一问题,本文提出了一种基于网格索引的查询框架,将当前访问的网格边缘到达查询点的最小时间代价作为上界值,与当前找到的第k大的时间代价作比较,当第k大的时间代价大于上界值时,终止算法.通过该方法,将查询范围大大缩小,避免了对路网的全局访问,极大地提高了kNN查询的效率.

再次,现有的针对静态对象的kNN查询,可以先对静态对象建立索引,在每次查询来到时,都访问这个固定不变的索引来提高查询效率.TOAIN算法[5]可以从预先计算的最近下坡对象中获取kNN查询结果,TEN*算法[6]对每一个节点预计算其子树节点的kNN结果,查询时只需要访问从查询点到根节点预存的kNN结果,就能获得查询点的kNN结果.但是对于在每次查询开始之前位置都会发生改变的移动对象,索引会随着位置的更新而失效.另外对于时间依赖路网来说,不同的查询时间会使每一个顶点对应着不同的kNN结果,索引也会随着查询时间的不同而失效.上述两种问题会导致巨大的索引更新代价,尤其是在索引建立代价更大的时间依赖路网中,所以此方法不适用于时间依赖路网下面向移动对象的近邻查询.针对这一问题,同样可以使用本文提出的查询框架,利用网格索引对移动对象的位置进行定位,在每次查询开始之前,可以快速地确定每个移动对象所属的网格,并且在网格扩展的过程中,对当前网格中的移动对象进行访问.

最后,时间依赖路网中的kNN查询往往是从用户的角度出发,找到k个能够最快到达用户所在位置的移动对象,但是如果从移动对象的角度考虑,会存在由于调度不合理而造成的时间浪费的情况.例如,一些当前被占用的移动对象,虽然需要先将当前用户送到目的地,再从目的地到达查询点,如果该目的地距离查询点位置很近,其到达查询点的时间代价甚至会比一些没有被占用的移动对象要小,但是由于处于被占用状态,所以无法参与调度.另一方面,对于用户来说,希望车辆在一个指定的时间范围内到达,这种情况下如果还是一味的追求时间代价最小,会导致一些距离查询点较近的移动对象提前到达,空车时间较长.所以本文同时考虑了被占用和未被占用的移动对象,并且提出了限制到达时间的k近邻查询,目的是在满足用户的时间要求的前提下,将移动对象的空车时间作为查询结果的选取标准,最终得到k个既满足用户要求,空车时间又最短的移动对象.

1 相关工作

1.1 静态路网中的kNN查询算法

解决静态路网中的kNN查询问题,最经典的方法是基于Dijkstra[4]的增量扩展方法INE算法[1],该算法无需索引结构.G-tree[3]设计了一个层次结构,将路网划分为由若干子图构建成的树结构,保存子图中边界点和非边界点之间的距离矩阵,采用自顶向下的方式来回答kNN查询.TEN*算法[6]同样使用将路网分解为树结构的方法,保存树中每个节点的部分kNN,在查询时,只需要访问从查询点到根节点中所有顶点的部分kNN结果,并且返回其中距离查询点最近的k个点.但是对于每次查询之前位置都要发生改变的移动对象来说,预存部分kNN结果的方法会导致索引更新的代价非常大.

1.2 时间依赖路网中的kNN查询算法

Cooke等[7]第一次提出并解决了时间依赖路网的最短路径查询问题.文献[8-9]借鉴INE的增量网络扩展的思路,从查询点开始向外扩展,直到找到k个查询点能够最快到达的移动对象,但无法解决查询方向从移动对象到查询点的问题.为提高在线查询的效率,一些索引结构被提出,文献[10]计算并预存了查询时间范围内几个子区间的最小时间代价,在查询时,利用类似A*算法的扩展方式,将最小时间代价作为启发值来使用,直到找到kNN查询结果.这种索引结构由于预估的时间代价和实际代价偏差较大,无法应用于大型路网.文献[11]提出了两种互补的索引结构紧密网络索引TNI和松散网络索引LNI,每个查询对象的TNI和LNI都是根据行驶时间的上限和下限预先计算的.如果查询点位于某一个对象的TNI单元中,那么该对象一定是查询点的最近邻结果,如果查询点不在任何对象的TNI单元中,而是在某一对象的LNI单元中,那么将该对象作为潜在的候选对象.该索引结构仅适用于静态的查询对象,当对象位置发生改变时,TNI和LNI的单元需要重新计算,更新代价大,因此无法用于解决针对移动对象的查询.

1.3 时间依赖路网中带有时间限制的最短路径查询算法

考虑时间限制的kNN查询算法较少,但有一部分工作研究了时间限制下的最优路径查询问题.杨雅君等[12]针对时间限制下的最优路径查询问题,基于“到达某个顶点的最早时刻可以通过到达其邻居的最早时刻计算得出”这一重要性质,提出了一种两阶段搜索算法.Omer等[13]则假定移动对象可以通过推迟出发时间或者在特定的地点停下来以避免在高峰时间的时间浪费,但是该研究只考虑如何避免浪费移动对象的时间,没有考虑到达时间限制.尽管kNN问题可通过执行多个最优路径查询来解决,但首先要搜索得到潜在的移动对象,计算出所有候选对象到查询点的最优路径,查询效率低.此外,上述方法由于时间依赖路网不能像静态路网一样进行反转,所以此类方法无法直接用来解决TD-LkNN查询.

2 问题定义

定义1.时间依赖有向路网：定义时间依赖有向路网G=（V,E,F,T）,其中vi∈V代表路网中的节点集合,（vi,vj）∈E代表路网中边的集合,f（vi,vj）∈F代表边（vi,vj）的时间依赖函数,T代表时间周期（例如一天中T=1 440 min）.

移动对象集合M为V的子集,为了方便理解,本文假设移动对象的位置在路网节点上[5].在实际应用中,不在节点上的对象可以表示为具有偏移量的对象,与节点之间的距离可以使用文献[5]中的公式进行计算.本文的移动对象具有被占用和未被占用两种状态,被占用对象的当前位置和目的地位置不同,td代表从移动对象当前位置到达目的地的时间代价,对于未被占用对象,当前位置和目的地相同,td=0.

定义2.时间依赖路网中的时间代价：在路网G中定义一条路径p={v1,v2,…,vn},该路径的时间代价表示为

式（1）中：t1=t,ti=ti-1+f（vi-1,vi）（ti-1）,i=2,...,n-1.

给定起点s,终点d和查询时间t,P为路网G中从s到d所有路径的集合,定义s到d的最小时间代价为P中所有路径的时间代价的最小值

定义3.空车时间：指定期待到达时间范围[T1,T2],时间上限为T2,定义空车时间Te（oi,q,t）如下

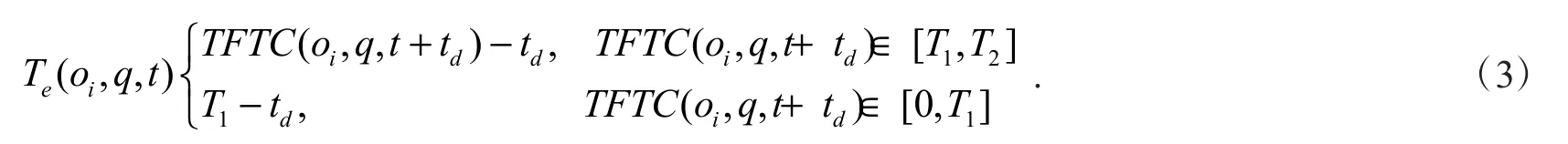
定义4.时间依赖路网中的LkNN查询：给定一个查询点q,一个时间段[T1,T2],一个移动对象集合M,查询时间t,一个值k,其中k≤|M|,和时间依赖有向路网G=（V,E,F,T）,TD-LkNN查询返回一个具有k个移动对象的集合R∈M,对于任意的oi∈R,满足条件：1）TFTC（oi,q,t）≤T2;2）Te（oj,q,t）≥Te（oi,q,t）,其中oj∈MR.

3 查询算法

3.1 TIGR算法

针对本文中移动对象到查询点的查询,最直观的方法是计算路网中所有移动对象到达查询点的时间代价和空车时间,从中选出最合适的k个作为查询结果,但是这样会导致查询范围过大,查询效率较低.为了避免对路网中移动对象的全局访问,本文使用了一种基于网格索引的查询框架,来找到查询点附近潜在的移动对象,只需要对这些移动对象进行访问即可,极大地缩小了查询范围.

为了计算候选集中移动对象到查询点的时间代价和空车时间,本文使用了TD-G-tree算法.TD-G-tree是一种计算时间依赖路网中的最快路径查询算法,该算法使用图分割将路网划分为若干个大小相似的子图,将每一个子图作为树中的一个节点构造出一棵平衡树.通过在树结构中保存大量的中间结果来加速查询的效率,算法具体细节可以参考文献[14].

TIGR算法的查询过程如图1所示,算法首先找到k个到达查询点的时间代价小于时间上限的移动对象,将这k个移动对象放入候选集中,并将其中第k大的空闲时间作为当前的上界Tk.取Tk和时间上限T2之间的最小值,用来划定一个欧式空间下的查询范围,如图1-a所示.当查询的网格范围大于图1-a中在Tk内部的范围时,说明当前网格边缘到达查询点的最小时间代价已经不满足查询要求,即外层网格中所有移动对象到达查询点的空车时间都大于Tk,不需要再对外层网格中的移动对象进行访问,算法达到终止条件.反之,如果查询的网格范围小于划定的查询范围,那么可以继续对下一层网格中的移动对象进行访问,如果访问到的移动对象ok’能够提供更小的上界值Tk’,则将当前的上界值更新为更小的值,可以进一步缩小查询范围,如图1-b所示.

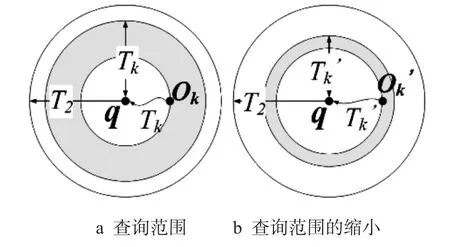
图1 TIGR算法思想Fig.1 The idea of TIGR algorithm

在查询之前,先将路网划分为若干个大小相等的网格,利用网格索引定位每个移动对象目的地的所属网格.以图2为例,{o1,o2,o3,o4,o5,o6}代表6个移动对象目的地的位置,括号中的内容代表从移动对象的当前位置到达目的地的时间代价.假设每个网格的宽度为10 km,路网中移动对象的最大行驶速度为1 km/min,那么可以得到,穿过每一个网格的最小时间代价为10 min.

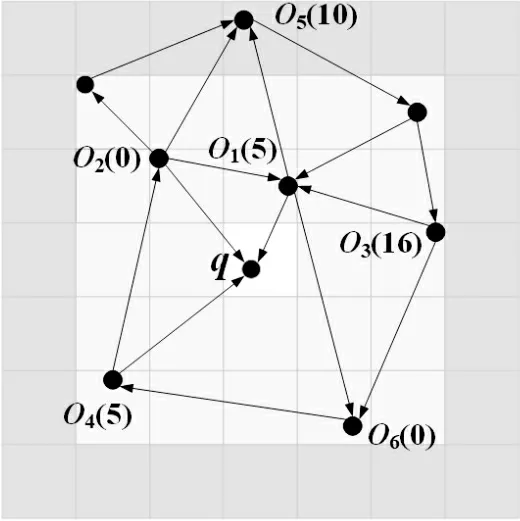
图2 TIGR算法详例Fig.2 Example of TIGR algorithm

在图中进行一个k=2的TD-LkNN查询,用户期望移动对象到达的时间段为[10,20]min.首先从查询点q所在网格开始,在扩展完第一层网格后,得到两个移动对象o1,o2,这两个移动对象到达q的时间代价分别为{10,15},小于时间上限20,空车时间分别为{5,15},将这两个移动对象放入候选集C中.此时候选集中移动对象数量达到了k个,Tk的值为15,此时路网中的空车时间上限UB的值也是15.接下来计算第二层网格边缘到查询点所在网格的最小时间代价,得到LB=10,小于当前的UB,说明外层网格中可能存在空车时间更小的移动对象,可以对第二层网格进行扩展,并且对其中的移动对象进行访问.第二层网格中的三个移动对象o3,o4,o5到达查询点的时间代价分别为{25,15,21},其中o3,o5不满足时间限制,不符合查询点要求,不再对其进行后续访问.计算得到对象o4到达查询点的空车时间为10,小于15,那么将对象o4放入候选集中,并且将Tk的值和UB更新为10.当对下一层网格进行扩展时,事先计算出第三层网格LB的值为20,说明外层网格中所有移动对象的目的地到查询点的时间代价大于UB,则空车时间也大于UB,不需要再向外扩展,最终返回候选集中空车时间最小的两个移动对象o1,o4作为LkNN查询结果.

算法的伪代码如算法1所示,给定时间依赖路网G,查询点q,网格索引L,查询时间t,和期望到达时间范围[T1,T2].算法以查询点所在网格为中心向外逐层扩展,直到得到k个满足条件的结果为止.算法前4行定义一些初始值,算法使用集合C来存储移动对象的候选集,集合H表示当前访问的网格,初始化为查询点所在网格,集合NH表示当前访问网格的外层网格集合.UB表示访问完NH中所有移动对象之后,当前候选集中第k个移动对象到达q的空车时间,初始化为时间上限T2.在扩展过程中,本算法维护一个从当前访问网格到查询点时间代价的下界值LB,用网格边缘与查询点所在网格之间的欧氏距离除以移动对象在路网中的最大移动速度得到.

算法第5行是对算法终止条件的判断.在第8-16行中,如果候选集中移动对象数量没有达到k个,则逐个访问网格中的移动对象,并将满足时间限制的放入候选集中,达到k个之后,需要将每一个满足时间限制的移动对象的空闲时间与候选集中第k个移动对象的空闲时间Tk进行比较,保留其中更小的值,并更新Tk的值.每访问完一层网格之后,算法17-19行将为下一层网格的扩展做准备.达到算法终止条件之后,20行返回候选集中的前k个移动对象作为LkNN的查询结果.

算法1:TIGR算法输入:路网G=（V,E,F,T）、查询点q、网格索引L、查询时间t、时间间隔[T1,T2]输出:q的TD-LkNN查询结果1 Let h be the grid containing q,2 Let C be the candidate set;3 Let UB be the upper bound of Te and initially set to T2;4 Let LB←0;5 While UB＞LB do 6 Let L（NH）be the set of objects in NH;7 for each o∈L（NH）do 8 ifC.size（）＜kthen 9 if TFTC(o,q,t)≤T2 then 10 compute Te(o,q,t);11 C←0;12 else 13 Tk=Min{k-th largest Te of objects in C,T2};14 ifTFTC（o,q,t）T2 then 15 if Te（o,q,t）＜Tkthen 16 C←o,Update Tk;17 H←HUNH,UB←Tk;18 Let NH be the set of grids that are neighbors of H but excluding the grids in H 19 Let DL be the minimum Euclidean distance from q to the edge of NH,LB←DL/Speedmax;20 Return top-k objects in C;images/BZ_68_1006_660_1212_686.png

3.2 TIGR_P查询算法

在TIGR算法中,部分移动对象在任意查询时间下的时间代价均大于时间上限.还存在时间代价过大的被占用对象和空车时间过大的未被占用对象,为了避免对此类移动对象的访问,本节提出了三种剪枝策略以及TIGR_P算法,对TIGR算法的查询效率进行改进.在介绍算法之前,先给出一些相关定义,然后详细介绍三种剪枝策略.

定义5.下界图：给定时间依赖路网G=（V,E,F,T）,定义下界图Gl=（Vl,El）为一个静态的有向图,其中Vl=V,El=E,所有边（vi,vj）E的权值都是时间依赖函数f（vi,vj）的最小值.

定义6.时间代价下界：在下界图Gl中给定一条路径pl={v1,v2,...,vn},路径pl的代价CGl（pl）定义为路径pl中所有边的权值之和.对于Gl中的查询起点s和终点d,pl代表从s到d所有的路径,定义时间代价下界LBC（s,d）=minp∈PlCGl（p）.

与静态路网相比,时间依赖路网中任意两点间最快路径的计算代价明显更大,所以对于在任意查询时间下,时间代价均大于时间上限的移动对象,可以先对时间依赖路网的下界图建立一个静态索引,通过该静态索引计算出移动对象到达查询点的时间代价下限,根据该时间代价下限来避免在时间依赖路网中对这些移动对象进行计算.基于此,本文提出了剪枝策略1.

策略1.下界图剪枝.根据定义5可以得到,如果利用下界图得到某一个移动对象oa到达查询点q的时间代价下界LBC（oa,q）大于移动对象ob到达查询点的真实时间代价,那么在任意查询时间,oa到达q的真实时间代价都会大于ob到达查询点的真实时间代价.

证明1：给定两个移动对象oa和ob,查询时间t和查询点q,如果LBC（oa,q）＞TFTC（ob,q,t）,那么对于任意的t∈[0,T],有

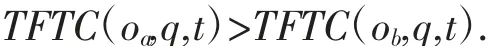
为了更好地使用这一策略,本文在下界图上建立了一个静态的H2H索引[15]来进行时间代价下界的计算.在给定时间范围[T1,T2]的前提下,部分移动对象到达查询点的最小时间代价会大于时间上限T2,从而无法成为查询结果,导致本次最小时间代价的计算是无效的.针对这一情况,可以先利用下界图计算每一个移动对象到达查询点的LBC是否大于T2,如果LBC大于T2,那么可以对该移动对象进行剪枝,不需要再计算该移动对象到达查询点的具体时间代价.

由于被占用的移动对象需要先从当前位置到达其目的地,所以存在这一段路程的时间代价过大的情况,对于这样的被占用对象,即使其目的地到达查询的时间代价非常小,也会存在整体时间代价大于时间上限的情况,所以要避免对此类移动对象的访问.基于此,本文提出了剪枝策略2.

策略2.被占用对象剪枝.根据定义1,被占用对象o拥有一个从当前位置到达目的地的时间代价td,当td大于T2时,可以对该移动对象进行剪枝.

证明2：对于被占用对象o,如果td＞T2,那么TFTC（o,q,t+td）+td＞T2.

对于未被占用的移动对象,由于从响应查询开始就处于空车状态,所以从当前位置到达查询点的整段路程,都是在产生空车时间的路程,由此可以得到,在给定时间范围[T1,T2]后,未被占用对象的最小空车时间为T1.如果当前路网中地空车时间最小值Tk＜T1,意味着当前路网中所有未被占用对象的空车时间都会大于Tk,即所有的未被占用对象都不会成为查询结果.所以在查询过程中需要不断判断Tk的值是否已经小于时间下限T1,如果满足该条件,则可以终止对后续所有未被占用对象的访问.基于此,本文提出了剪枝策略3.

策略3.未被占用对象剪枝.对于未被占用对象,如果从移动对象到达查询点的最小时间代价小于T1,并且当前Tk＜T1,那么该移动对象可以被剪枝.

证明3：由公式3可知,对于未被占用对象o,如果TFTC（o,q,t+td）+td＜T1,则Te（o,q,t+td）=T1.已知Tk＜T1,则Te（o,qt+td）＞Tk.

本算法的查询框架与算法1相同,伪代码也与算法1类似,只在剪枝策略的使用上有所不同.在算法1第13行,得到Tk后,使用剪枝策略3,判断当前候选集中第k个移动对象到达查询点的空车时间Tk是否小于时间下限T1,如果满足条件,则停止对未被占用对象的访问.在算法1的第14-16行,需要计算网格中每个移动对象到查询点的具体时间代价和空车时间之前,使用剪枝策略1和2,先计算每一个移动对象到达查询点的时间代价下界,如果时间代价下界大于时间上限T2,则该移动对象被剪枝.同时对于每一个被占用对象,判断td是否大于时间上限T2,如果满足条件,则该被占用对象被剪枝.

4 实验验证

4.1 实验条件

本文算法均由C++语言编写,使用GNN GCC进行编译.实验平台为Linux（Ubuntu18.04）操作系统,CPU型号为Intel（R）Xeon（R）W-2245,内存256 GB.

4.2 实验数据

本文使用纽约市真实路网进行实验,根据文献[14],本文同样模拟每天的三个时间段,分别是早高峰之前,早高峰与晚高峰之间和晚高峰之后,使用四个拐点（x1,y1）,（x2,y2）,（x3,y3）,（x4,y4）拟合成一条分段线性函数,作为边的时间依赖函数.在每天的1 440 min中,拐点横坐标x1=0,x4=1 440,x2∈[510,570）,x3∈[990,1 070）,x2,x3是在对应时间范围内随机选取的一个值.对于纵坐标,本文首先设置两个速度指标,包括非高峰期的行驶速度sp1∈[500,900]m/min,和高峰期的行驶速度sp2∈[300,750]m/min,对于路网中长度为l（u,v）的边（u,v）,纵坐标的值

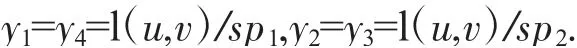
本文实验参数设置如表1所列,加粗数字代表实验参数的默认值,其中比例θ代表被占用对象占移动对象总数的比例,时间范围γ代表在指定时间点T上下各浮动5 min.

表1 实验参数设置Tab.1 Parameter settings

本文默认数据集为纽约市路网NY,NY中移动对象数量默认为10 000.本文从纽约路网中抽取三个子网NY1,NY2,NY3作为不同的数据集,子网点和边的数量如表2所示.在不同数据集的实验中,移动对象默认数量不同,数据集NY1中,默认为1 250个,NY2中,默认为2 500,NY3中,默认为5 000.

表2 实验数据集Tab.2 Datasets

4.3 结果分析

本文分别对TIGR和TIGR_P查询算法进行实验,用来比较在使用不同的最快路径查询算法时,TIGR与TIGE_P算法的查询效率.本文将最快路径查询算法TD-Dijkstra[16]与本文的查询框架结合,作为本文的对比实验.其中使用TD-G-tree的算法分别表示为TIGR（G）和TIGR_P（G）,使用TD-Dijkstra的算法分别表示为TIGR（D）和TIGR_P（D）.每组查询在路网中随机选取1 000个查询点,并且在[0,1 440]内随机选取一个时间点作为查询时间,将1 000次查询的平均时间展示在实验图中.

（1）k值.由图3可以看出,在使用TD-G-tree和TD-Dijkstra进行查询时,TIGR_P算法的查询效率均比TIGR提升一个数量级左右,甚至使用了剪枝策略的TIGR_P（D）的查询时间要比没有使用剪枝策略的TIGR（G）还要短,体现了本文所提剪枝策略的高效性.另外,两种算法的查询时间都随着k值的增大而增加,这是由于k值越大,查询范围越大,需要访问的移动对象数量也随之增加.但由于时间上限的限制,当k值较大时,位置在时间上限对应的网格范围之外的移动对象不需要被访问,查询时间增速相对变缓.

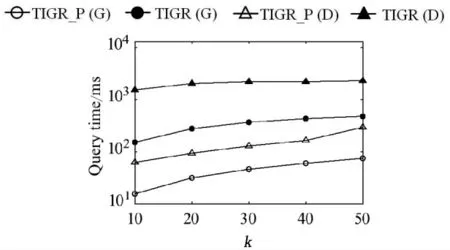
图3 k值对查询效率的影响Fig.3 Query efficiency vary k

（2）移动对象数量|M|.由图4可以看出,随着移动对象数量的增加,使用TD-G-tree的查询算法的查询时间逐渐变短.这是由于随着移动对象数量的增多,其在路网中的密度也随之增大,在k值不变情况下,查询所需扩展的空间范围越小,查询时间越短.相反,使用TD-Dijkstra的两种算法的查询时间都随着移动对象数量的增多而增加,这是由于TD-Dijkstra使用在线扩展的方式进行最快路径查询,计算代价较大,当移动对象数量越多,进行的计算次数越多时,查询时间就会越长.但总体来看,TIGR_P算法的查询效率仍比TIGR算法提高了1~2个数量级.

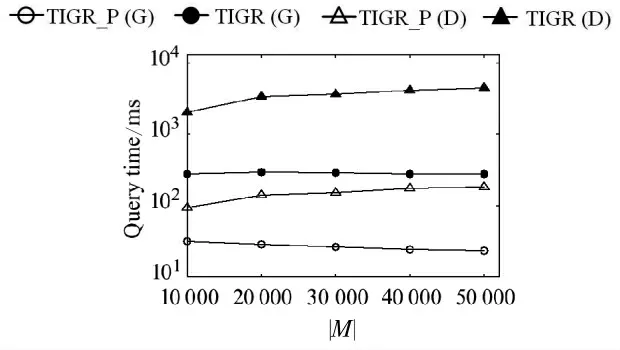
图4 |M|对查询效率的影响Fig.4 Query efficiency vary|M|

（3）网格宽度L.由图5可以看出,使用TD-G-tree和TD-Dijkstra进行查询时,网格大小对两种算法的查询效率影响都较小,这是由于在网格较大时,需访问的网格数量虽然较少,但每个网格中移动对象数量较多,而网格较小时则相反,因此总体查询响应时间变化不大.

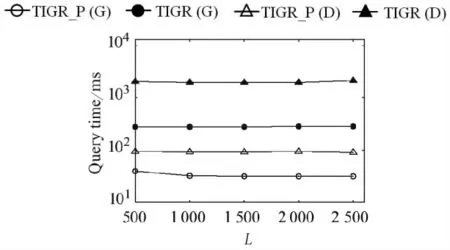
图5 L对查询效率的影响Fig.5 Query efficiency vary L

（4）数据集Dataset.由图6可以看出,两种算法的查询时间都随着数据集的增大而增大.这是因为在移动对象密度不变的前提下,数据集的增大会导致查询范围的扩大.而对于TIGR_P,剪枝策略的使用会相对缩小查询范围,所以查询时间的增加相对平缓.值得注意的是,使用TD-Dijkstra的查询算法受数据集的影响更大,这是由于在数据集变大导致查询范围变大时,利用TD-Dijksrta作为查询过程中的最快路径查询时,查询效率会明显变低.

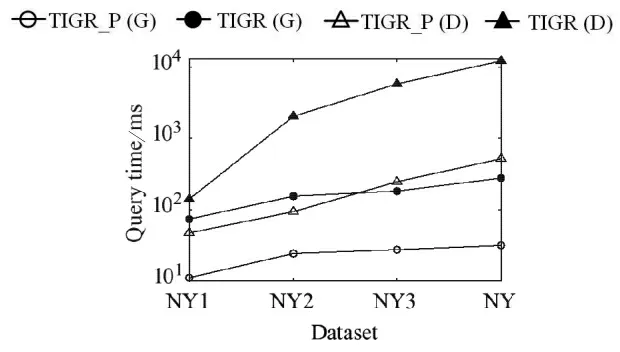
图6 Dataset对查询效率的影响Fig.6 Query efficiency vary Dataset

（5）比例θ.由图7可以看出,对于TIGR_P,随着被占用对象比例的增加,使用TD-G-tree和TDDijkstra的查询算法的都随之增大.相反,TIGR的查询时间是随着被占用对象比例的增加而减小.这是由于,根据定义3,未被占用对象能够提供的最小空车时间是T1,但由于被占用对象存在从当前位置到目的地的时间代价,所以往往能够提供小于T1的空车时间,从而更快的满足算法终止条件,使查询范围减小,查询效率提高.但是由于剪枝策略3的存在,减小了未被占用对象对查询效率的影响,所以使用了剪枝策略的TIGR_P能够让查询效率受查询环境的影响更小,更稳定.

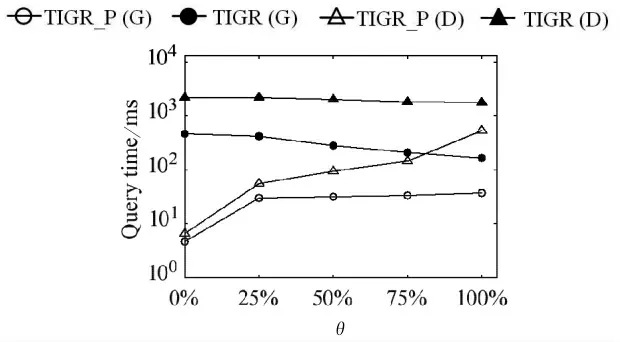
图7 θ对查询效率的影响Fig.7 Query efficiency vary θ

（6）时间范围γ.由图8可以看出,使用TD-G-tree和TD-Dijkstra的查询算法的查询时间都随着时间点的增大而增大.这是因为随着时间点的提高,距离查询点较近的移动对象提供的空车时间会更长,为了获得空车时间更短的移动对象,查询范围会随之扩大.

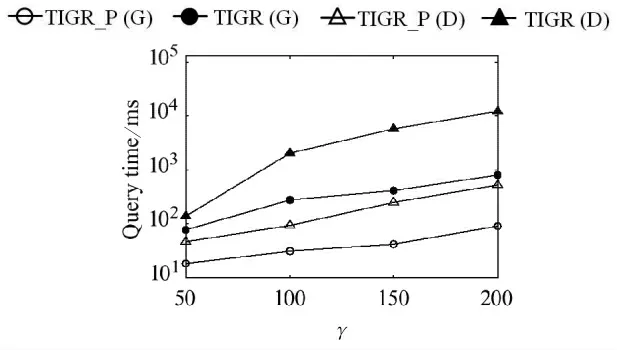
图8 γ对查询效率的影响Fig.8 Query efficiency vary γ

5 小结

与传统的kNN查询相比,带有到达时间限制的k近邻查询更具有现实意义.本文提出了一种TIGR算法,首先利用基于网格索引的框架结构确定移动对象的候选集,再计算候选集中移动对象到达查询点的具体时间代价和空车时间,并提出了基于剪枝策略的TIGR_P查询算法.实验结果表明,所提的TIGR_P算法能够高效的实现查询,比TIGR算法执行速度快一个数量级左右.下一步工作中,我们将考虑进一步缩小搜索范围,增强剪枝效果,提高查询效率.