基于拉格朗日插值的教与学动态组自适应算法
2022-10-17张义民王一冰
张 喆,张义民,张 凯,王一冰
(沈阳化工大学 装备可靠性研究所,辽宁 沈阳 110142)
0 引 言
目前人工智能优化算法在经典问题上得到了越来越广泛的应用,如工程优化[1]、图像处理[2]、机械设计[3]等。然而,大多数优化算法还是存在陷入局部最优和处理复杂问题的收敛速度慢等缺陷[4],因此,解决上述问题成为当前学者普遍关注的热门问题。
为了解决上述问题,许多学者对此进行了努力。根据努力方向分为以下两点,第一种是对局部搜索改进来加强算法的寻优能力,文献[5]通过将自适应策略、竞争性的局部搜索选择和增量种群规模策略这3种策略集成到标准ABC算法中,提高了算法的性能;文献[6]将局部搜索方法与进化算法相结合,使混合算法结合了随机优化和确定性优化的优点,摆脱了搜索最优解的能力弱的问题;文献[7]针对灰狼算法具有易陷于局部最优缺点,改进收敛因子和引入动态权重,提高了局部搜索能力;文献[8]从分布在搜索空间中的局部向量中提取良好的向量信息,该向量可以跳出局部最优进行进一步优化。另一种是通过对全局搜索改进来加强算法的寻优能力,文献[9]基于布谷鸟3种串行行为,提出了一种多策略串行框架,提高了学习策略的全局搜索能力;文献[10]采用改进的参数自适应方法,通过加入加权均值策略,避免了过早收敛,实现了最优解的全局优化;文献[11]提出一种改进TLBO的算法,称为基于教学的动态组策略优化算法(DGSTLBO),通过加入动态群策略来求解全局优化问题,从而提高算法的全局搜索能力。
不同策略的改进都在一定程度上提高了算法的性能,但是还是避免不了算法陷入局部最优、收敛速度慢和求解精度低的情况。虽然DGSTLBO算法在全局搜索上表现出极其优异的搜索性能,但在解决一些复杂的优化问题时,它仍然存在求解精度低、收敛过早和收敛速度慢的情况[12]。因此,为了使DGSTLBO算法的性能更加完善,本文加入了一种拉格朗日插值的局部搜索,通过选用拉格朗日插值作为局部搜索方法可处理求解多维度优化问题的加速收敛[13],使得求解精准度更高,为了平衡算法的全局搜索能力和局部开发能力,本文引入了自适应参数策略,以自适应地确定是否使用拉格朗日插值局部搜索在上一代的性能。最终提出了一种基于拉格朗日插值的教与学动态组自适应算法(ADLTLBO)。
1 DGSTLBO
DGSTLBO算法是一种有效的全局优化方法,通过随机学习策略或相应群体的量子行为学习策略进行概率学习,该算法的主要内容为分组和动态组策略。其伪代码如算法1所示。
算法1:DGSTLBO算法
(1)Begin
(2) 初始化N(种群大小),D(维度),gen(迭代次数),genmax(最大迭代次数)。
(3) 初始化学习者, 计算出所有学习者的适应值。
(4) 执行算法2分组;
(5)while(没到最大评估次数就不停止)

(7) 更新班级的老师和每组的平均值;
(8) 执行算法3动态组策略;
(9)endfor
(10)endwhile
(11)end
1.1 分 组
将学习者分成小范围的群体,以增加种群的多样性,进而使每个组的组内成员在搜索空间中搜索更有前景的区域。首先选择第一批m个学习者,并将其作为一个组,然后从当前的学习者中移除选定的m个学习者,当所有的学习者被分成组时,算法终止。其伪代码如算法2所示。
算法2:分组
(1)Begin
(2) 将所有学习者按其结果的降序排列
(3)while(排序的学习者不能为空)
(4) 评估从第一个学习者到每个学习者的距离;
(5) 按照距离的升序对所有学习者进行排序;
(6) 选择前m个学习者, 并将其设置为一个组;
(7) 从学习者中删除当前组学习者;
(8)endwhile
(9)end
1.2 动态组策略
通过引入动态群体学习,提出的改进学习策略。当群体迭代到一定程度后,周期性地改变群体,使信息交换覆盖班级中的所有学习者。该策略主要包括教师阶段的学习者更新和学习者阶段的学习者更新。
1.2.1 教师阶段的学习者更新
下面给出了更新学习者X学习的公式
newX=X+r*(Teacher-TF*GroupMean)
(1)
式中:Teacher表示全班最好的学习者;TF是一个教学因子,它决定要改变的均值的值;r是一个向量,其元素是[0,1]范围内的随机数。
1.2.2 学习者阶段的学习者更新
下面给出了DGSTLBO中X学员量子行为学习的更新公式
tempX=φ*GroupTeacher+(1-φ)*Teacher
(2)
newX=tempX+β|GroupMean-X|*ln(1/u)
(3)
newX=tempX-β|GroupMean-X|*ln(1/u)
(4)
其中,GroupTeacher表示组中最好学习者;Teacher表示全班最好的学习者;GroupMean表示学习者X自己相应组的平均值;φ、β和u是向量,其中每个元素都是[0,1]范围内的随机数。动态组策略伪代码如算法3所示。
算法3:动态组策略
(1)Begin
(2)for对每一组
(3)for当前组的每个学习者X%教学阶段
(4)TF=round(1+rand(0,1));

(6) 按式(1)更新学习者;
(7)endfor
(8) 如果f(newX)比f(X)的值好, 则以newX更新X;
(9)endfor
(10)for当前组的每个学习者X%学习阶段
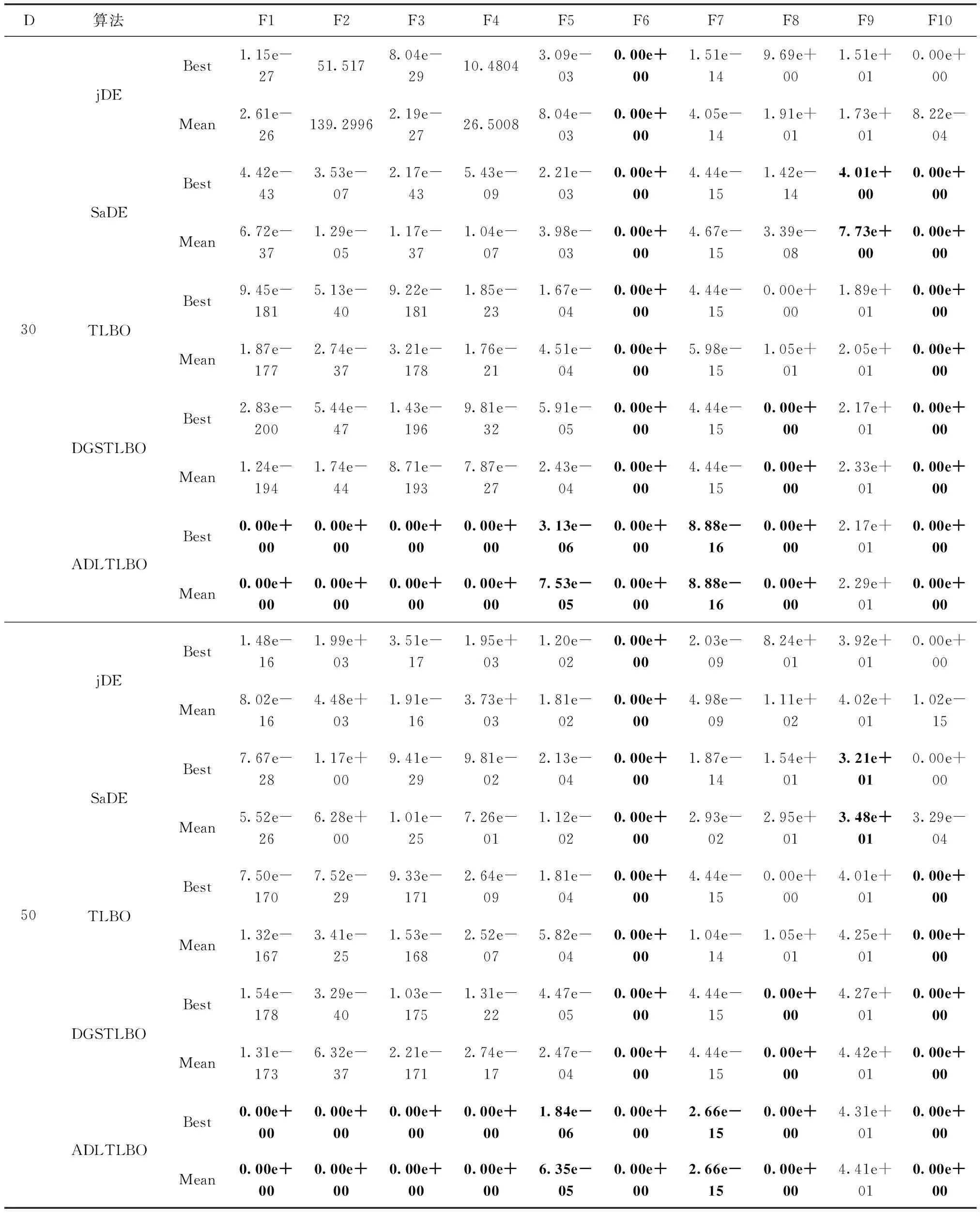
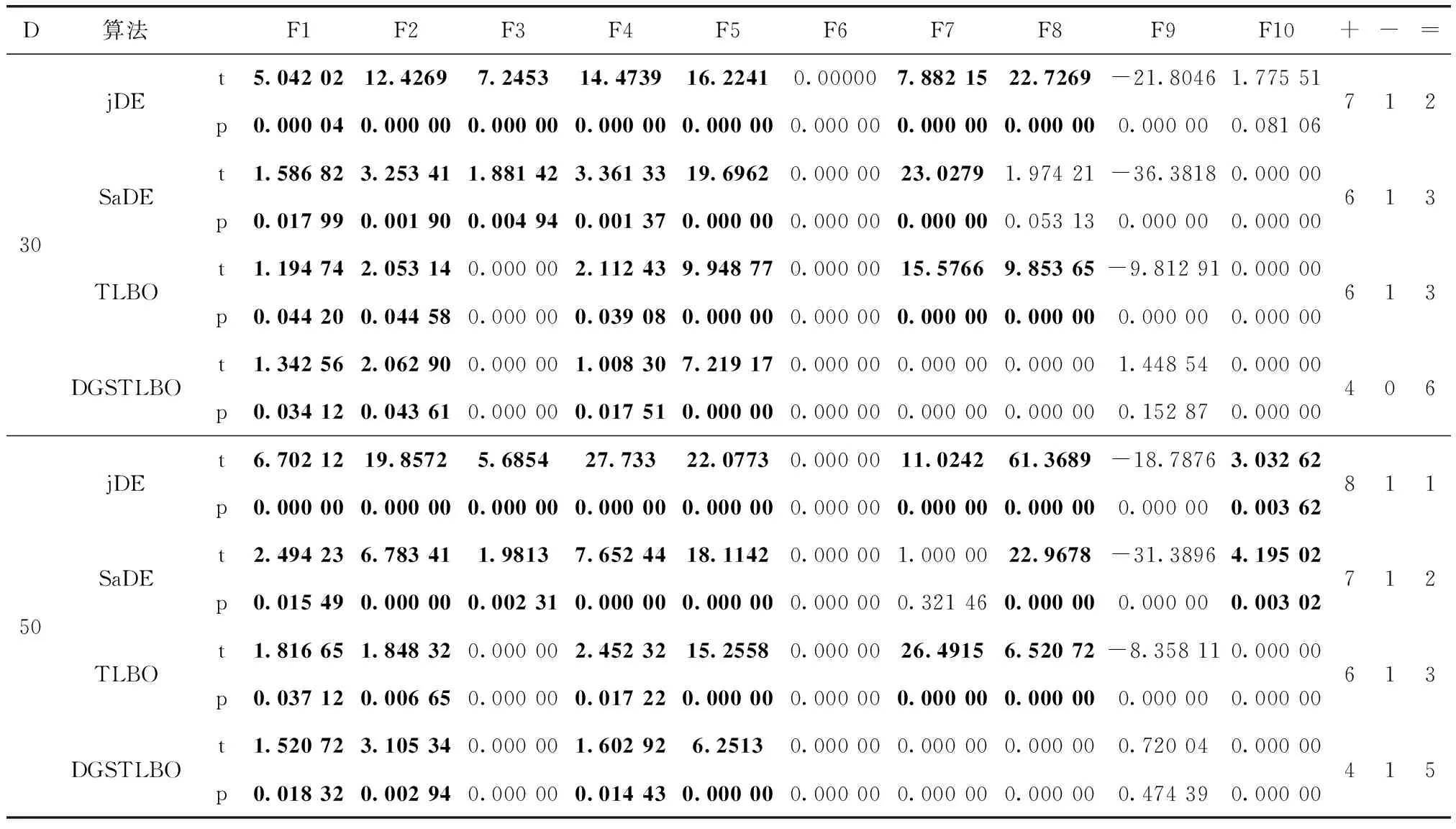
(11)ifrand(0,1) (12) 执行原TLBO的学习策略; (13)else (14) 按式(2)进行量子行为学习; (15)ifrand(0,1)<0.5 (16) 按式(3)进行量子行为学习; (17)else (18) 按式(4)进行量子行为学习; (19)endif (20)endif (21) 如果f(newX)比f(X)的值好, 则以newX更新X; (22)endfor (23)endfor (24)ifmod(gen,P)=0 (25) 执行算法2分组; (26)end (27)end 本文提出的ADLTLBO算法基础思想:为了完善DGSTLBO算法在局部搜索上的计算能力以及收敛速度,增强该算法的有效性和可用性,在DGSTLBO算法的基础上加入拉格朗日插值局部搜索和自适应参数策略。由于拉格朗日插值可以提高算法的开发能力,并帮助加速收敛速度,因此通过采用一种新的自适应参数策略将其引入到DGSTLBO中。本文算法包括两个主要元素:带有拉格朗日插值的局部搜索、自适应参数策略。 (5) 也可以用式(6)表示成一个二次函数,通过求解二次函数的最值来更进一步优化解 P(xj)=a(xj)2+bxj+c,j=1,…,D (6) 其中 (7) (8) (9) (10) (11) (12) 拉格朗日插值算法的伪代码如算法4所示。 算法4:拉格朗日插值算法 (3) 按式(6)写出拉格朗日插值多项式; (4)if(I≠0) (5)if(a>0) (7)elseif(a=0 andb=0) (9)else (12)endif (13)else (16)endif 引入LSLI的主要目的是提高DGSTLBO算法在已经具有最佳适应度xbest的个体的邻居处进行局部搜索的开发能力,为了能够获得更加精确的全局最优解,针对当时的全局最优位置作二次拉格朗日插值。 (13) (14) 其中,xbest是j维中最佳个体参数,Rj是j维中xbest的搜索半径。可以根据式(15)以目前种群的分布情况自适应地调整 (15) 式中: max(xj), min(xj) 分别是当前维度最大值、最小值,N是种群的数量。 算法5:LSLI算法 (1)输入: 种群X, 维数D, 种群边界up、low, 最佳个体xbest, 最佳适应值f(xbest)。 (2)输出:xbest,f(xbest)。 (3)%使用算法4在xbest的每个维度上进行局部搜索 (5) 初始化xbest相邻的两个临时个体x1和x2; (10)end 在ADLTLBO算法中,使用自适应参数策略将LSLI插入到DGSTLBO算法中,首先在整个搜索空间中快速地探索问题的解决方案。然后,该方案根据LSLI率(LR)决定是否使用LSLI。最后,该方案自适应地确定是否使用LSLI在发现的最佳解决方案附近进行局部开发,并更新LR,如式(16)所示 (16) 算法6:ADLTLBO算法 (1) 初始化种群N, 维度D,MaxFEs(评估的最大值),m(每组大小), 初始化LR,LRmax和LRmin,xup,xlow。 (2)初始化学习者, 计算出所有学习者的适应值; (3) 执行算法2分组; (4)%评估最初个体记住最佳xbest和最佳适应值f(xbest); (5)While(G (6)%自适应参数策略 (7)if(rand(0,1) (10)end (11) 更新班级的老师和每组的平均值; (12) 执行算法3动态组策略记录并更新; (13)endwhile 步骤1 初始化种群:种群个数N、维度D、重组周期p、每组成员数m、最大迭代次数MaxDT。学习概率pc,拉格朗日插值局部搜索率LR,评估的最大值MaxFEs。 步骤2 计算适应值:计算出每个个体的适应值,并记录最优个体与最优适应值。 步骤3 对种群个体进行分组:对所有学生进行排序,评估第一名与每个学生的距离,然后按照距离排序,最后选择m名学生作为一组。 步骤5 更新各组中的老师:计算各组适应值,选择成绩最好者作为老师。 步骤6 进行教学:按式(1)进行教学。 步骤7 进行学习:当rand<0.5时,进行原TLBO算法学习,当rand>0.5时,采用量子行为学习。记录并更新最优个体与最优适应值。 步骤8 检查是否满足终止条件,若满足,则迭代止,否则重新分组并转至步骤4。 本文所有进行的实验均是在PC机上运行,PC机的配置如下:Intel(R) Core(TM) i7-4712MQ CPU @ 2.30 GHz、内存为8 GB,Windows10操作系统,仿真软件为Matlab R2015b。 为了验证本文所提算法的性能,选取了经典的10个基准函数数值优化函数进行了实验验证,将改进算法与DGSTLBO算法、TLBO算法、SaDE算法和jDE算法进行对比实验。 为了测试算法在不同函数上的性能,本文选择了10个基准函数进行操作,根据函数的性质分为两大类,其中函数F1~F6为单峰函数,主要测试算法的求解精度。F7~F10为多峰函数,用来测试算法跳出局部极值的能力。每个函数的搜索范围和理论最优值已在表1中给出。 表1 函数的详细数值 为减少统计误差,在30维和50维的情况下,所有算法种群规模都设定为50,每个函数独立模拟30次,算法使用相同的停止准则,即达到一定数量评估次数(FEs)。在实验中,FEs取值为10万。本文算法参数m=5,p=5,pc=0.5。LR=0.5,LRmax=0.9,LRmin=0.1。其余对比算法的参数与原文献相同。 为了更清晰地观察改进后算法的收敛效果,通过10个测试函数在30维的收敛曲线来将ADLTLBO算法与DGSTLBO算法、TLBO算法、SaDE算法和jDE算法的收敛情况作对比,在相同函数下的收敛曲线如图1所示。可以从图1中明显发现,单峰函数F1~F5中,由于加入了拉格朗日差值局部搜索,ADLTLBO求解精度和收敛速度大幅度提高,在整个迭代过程中一直持续更佳的收敛速度,寻优效果大幅提升。虽然ADLTLBO、DGSTLBO、TLBO、SaDE和jDE在函数F6都收敛到了理论最优,但是ADLTLBO在收敛速度上还是超过了其余4个算法。在多峰函数F7、F8和F10中,由于加入了自适应参数策略,ADLTLBO无论是在收敛速度还是求解精度上都优于DGSTLBO、TLBO、SaDE和jDE,更容易跳出局部极值。研究结果表明,在函数F1、F2、F3、F4、F5、F6、F7、F8和F10上ADLTLBO算法结果更具有优势,收敛速度更快。 通过对5个算法分别在30维和50维的10个测试函数上独立运行30次得到的均值和最优值实验结果作对比,好的结果用粗体表示,见表2。然后,采用T检验[14,15]对算法进行统计分析,通过得到的t值和p值来比较结果之间的差异,见表3,显著结果用粗体标出。两个算法的T检验采用了双尾检验,显著性水平为0.05,符号“+”、“-”和“=”分别表示在相同的运行数量下本文算法的性能明显优于、明显劣于和类似于所比较的算。 如表2所示,30维和50维下ADLTLBO在函数F1、F2、F3、F4、F5和F7中的结果都比其它算法要好,并且在函数F1~F4中达到了理论值,在函数F6、F8和F10多个算法都达到了理论值,但是可以从图1中看出ADLTLBO的收敛速度明显比其它算法要好。通过在10个基准函数的测试下,ADLTLBO在大多数情况下取得了较好的结果,在30维和50维下T检验结果中,ADLTLBO算法优良率分别占92.5%和90%。由此可以验证ADLTLBO算法的局部寻优能力更强、收敛速度更快和求解精度更高。 为了完善DGSTLBO算法在局部搜索上的计算能力及收敛速度的不足,本文提出了一种基于拉格朗日插值的教与学动态组自适应算法(ADLTLBO),其同时利用了DGSTLBO算法和拉格朗日插值法的优点,为了平衡算法的全局搜索能力和局部开发能力并加入自适应的参数策略,使拉格朗日插值在最佳个体附近执行,本文算法的性能通过对10个基准测试函数在30维和50维与其它4种经典算法进行了比较。从分析和实验结果表明,本文算法能有效避免陷入局部最优,使得求解精准度更高,收敛速度更快。因此,采用拉格朗日插值的局部搜索技术使本文算法能够利用局部更有效地提供信息,更频繁地生成更高质量的解决方案。所提出的具有自适应参数策略的拉格朗日插值局部搜索方案可以插入任何其它教与学算法中,以提高其局部开发能力。 表2 30维和50维测试函数结果对比 表3 30维和50维t检验结果对比2 ADLTLBO算法
2.1 拉格朗日插值
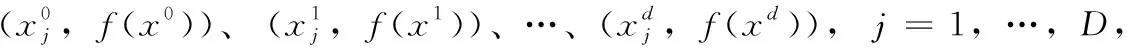

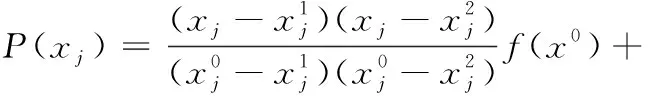
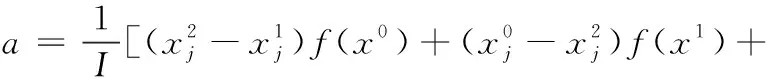

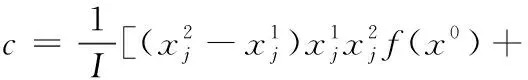
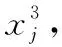
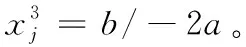
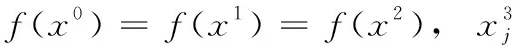
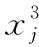
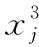
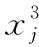
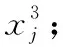
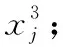
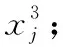
2.2 拉格朗日插值的局部搜索(LSLI)
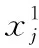
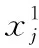

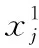
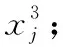
2.3 自适应参数策略
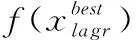

2.4 算法流程
3 数值实验分析
3.1 基准函数

3.2 参数设置
3.3 实验结果分析
4 结束语