不等式“能成立”,多思维视角切入
——一道含参存在性问题的探究
2022-10-17张彬
张 彬
(江苏省西亭高级中学,江苏南通,226300)
涉及不等式“能成立”(或存在性成立)问题,是高中数学中有关函数与不等式的一个重点与难点,往往以含参不等式形式出现,是一类极具交汇性、综合性与创新性的复杂应用问题,难度较大,形式多样.此类不等式“能成立”问题知识融合性强,解决时有一定的经验规律与技巧方法可循,能有效考查学生“四基”的落实情况,具有非常好的选拔性与区分度,倍受关注.
1 问题呈现
问题 (云南省昆明市2022届高三“三诊一模”摸底诊断测试理科数学·21)设函数f(x)=x2-axlnx,a∈R.
(1) 若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 若存在x0∈[1,e],使得f(x0)<-e(a+e)成立,求a的取值范围.
此题是新高考中比较常见的一类不等式“能成立”(或存在性成立)问题,以含参函数为问题背景,通过导数的几何意义来构建,求解曲线上相关点处的切线方程;结合限定区间的给出,构建存在条件背景下的涉及参数的不等式成立问题,由此来求解参数的取值范围.
这里以不等式“能成立”(或存在性成立)问题创设,通过含参存在性问题的构建,结合不等式成立来设置,可以借助不等式成立的背景,从直接构建函数、分离参数等方法构建相应的函数等常见的思维视角切入,也可以通过存在性问题成立的充要条件来合理分析与推导等.
2 问题破解
解析:(1) 由于函数f(x)=x2-axlnx,a∈R的定义域为(0,+∞).
若a=1,则f(x)=x2-xlnx,求导可得f′(x)=2x-(lnx+1).
而f′(1)=1,f(1)=1.
从而曲线y=f(x)在点(1,1)处的切线方程为y-1=1×(x-1),即y=x;
(2) 方法1:(参考答案中的方法——同除简化函数法)
分析:考虑到直接对函数f(x)求解相应的最小值,导数的运算量比较大,可以通过转化,考虑将不等式f(x)<-e(a+e)两边同时除以x,从而将题干中的相关的复杂函数“axlnx”转化为简单函数“alnx”来处理,有效简化函数来分析与处理.
解析:由不等式f(x)<-e(a+e),整理可得x2-axlnx+e(a+e)<0.
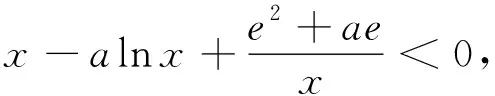
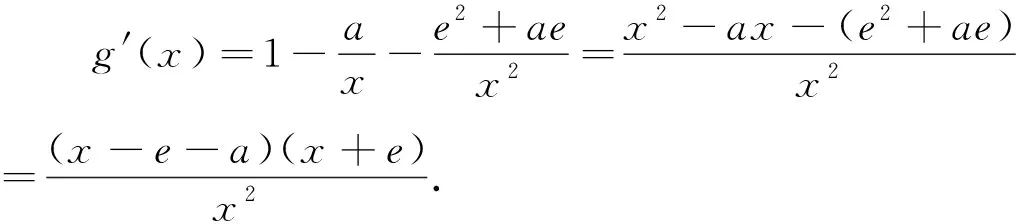
因为x∈(0,+∞),所以x+e>0,令g′(x)=0,得x=e+a.
若e+a≤1,即a≤1-e时,g(x)在[1,e]上单调递增.
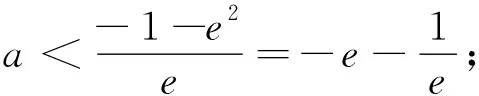
若e+a≥e,即a≥0时,g(x)在[1,e]上单调递减.
只需g(e)=e-a+e+a<0,不成立;
若1 方法2:(参数分离法) 分析:考虑到要求解参数a的取值范围,通过对不等式f(x)<-e(a+e)恒成立进行合理化归与整理,结合变量的取值范围进行分类讨论,进而结合分离参数,并利用构建函数法将问题转化为a 解析:由不等式f(x)<-e(a+e),整理可得a(xlnx-e)>x2+e2. 当x=e时,a∈∅; 由于x∈[1,e),可得2x(xlnx-e)<0,(lnx+1)(x2+e2)>0,故g′(x)<0. 则知函数g(x)在[1,e)上单调递减. 方法3:(逆否命题等价转化法) 分析:通过对参数a进行分类讨论,当a≤0时,结合函数的单调性以及函数的最值,结合不等式的性质与求解来确定参数a的取值范围;而当a>0时,结合互为逆否命题的等价性思维,利用不等式的性质以及函数的单调性来确定此时不满足条件;综合分类讨论法进而来确定参数a的取值范围. 解析:由于当x∈[1,e]时,xlnx和x2均是单调递增. 则当a≤0时,f(x)=x2-axlnx在[1,e]上单调递增,此时f(x)min=f(1)=1. 而当a>0时,对任意x∈[1,e]. 由f(x)+e(a+e)=x2-axlnx+e(a+e)=(e-xlnx)a+e2+x2. 而由于x∈[1,e],可得1≤xlnx≤e,即e-xlnx≥0. 所以f(x)+e(a+e)=(e-xlnx)a+e2+x2>e2+x2>0恒成立. 由此可得,当a>0时,不存在x0∈[1,e],使得f(x0)<-e(a+e)成立; 变式1 已知函数f(x)=x2-(a+2)x+alnx,a∈R. (I) 若a=-2,求曲线y=f(x)在x=1处的切线方程; (II) 讨论函数f(x)在[1,e]上的单调性; (III) 若存在x∈[1,e],使得f(x)≤0成立,求实数a的取值范围. 而f′(1)=0,f(1)=1,所以所求切线方程为y=1; 即当a≤2时,f′(x)≥0,此时函数f(x)在[1,e]上单调增; (Ⅲ)方法一:(分类讨论法) 当a≤2时,由于函数f(x)在[1,e]上单调增,则知函数f(x)的最小值为f(1)=-a-1,可得-1≤a≤2. 当a≥2e时,函数f(x)在[1,e]上单调减,则知函数f(x)的最小值为f(e)=e2-(a+2)e+a. 综上,a≥-1,所以a的取值范围是[-1,+∞). 方法二:(分离参数法)(略) 涉及不等式“能成立”(或存在性成立)问题,解决的基本策略就是“含参”转化与“分参”处理两个基本思维角度,具体解决时,思维技巧方式多样,巧思妙解,利用不等式“能成立”的背景,综合不等式的性质、不等式的求解以及函数的基本性质等,借助函数的合理构造,函数、方程与不等式三者之间的巧妙转化,利用熟知的数学模型来分析与破解不等式的“能成立”问题,提升数学品质,提高数学能力,培养数学核心素养.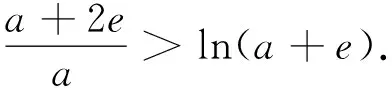
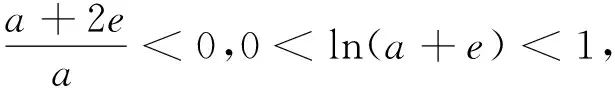
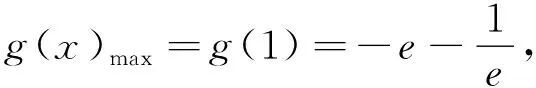
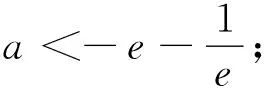
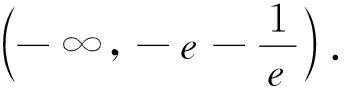
3 变式拓展
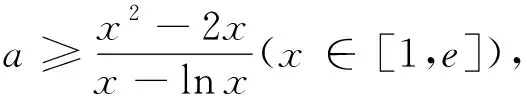
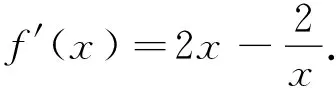
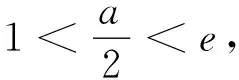
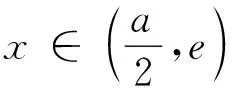
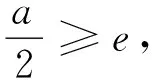

4 解后反思
