函数思想在数列最值中的应用

徐龙彪

(哈尔滨师范大学教师教育学院，黑龙江哈尔滨，150025)

函数思想是通过分析问题的数学特征建立目标函数，从而利用函数的性质和图象去解决问题.用函数思想解题要掌握函数性质包括单调性、奇偶性、最值、周期性与函数的图象.函数思想在数列中以构造函数得到解题所需要的目标函数为途径解题.构造函数之前一定要对题目充分.挖掘，找出隐含条件，这是函数思想在解题中的关键，只有通过充分挖掘找出问题内在的联系，才能构造函数解决问题[1].

1 数列的函数特性

数列作为特殊的函数，其通项公式与求和公式和函数密不可分.函数与数列是一般与特殊的关系，例如：

等差数列的通项公式an=a1+(n-1)d⟺an=dn+(a1-d)，可以看作是关于n的一次函数an=An+B(A，B为常数、n∈N*)；

用函数思想解决数列问题不一定要以通项公式或求和公式构造函数，可以根据代数式的具体结构去构造有利于解题的目标函数，用函数思想解决数列最值问题归根到底就是将数列问题构造函数用函数最值解题.

2 函数思想在数列中的应用类型

数列最值问题一般包括数列最大或最小项、等差数列前n和Sn、等比数列前n项积最值.

2.1 用函数思想解决数列最大或最小项

(1) 求数列{bn}的通项公式；

例4数列{an}的通项公式是an=-2n2+29n+3，求{an}中最大项的值.

小结：有关于数列最大或最小项的问题，最常见的就是上述四类.

(4) 第四类数列的最大或最小项问题最为简单，题目会直接给出关于n的二次函数的通项公式，直接利用函数的性质进行解题.

2.2 用函数思想解决Sn最值问题

用函数思想解决数列中Sn最值问题包括等差数列前n和Sn的最值、等比数列前n积的最值、等比数列中几项和的最值.

例5等差数列{an}中，已知a1=20，前n项的和为Sn，且S10=S15，求当n取何值时，Sn取得最大值，并求出它的最大值.

例6设等比数列{an}满足a1+a2=10，a2+a5=5.求a1a2a3…an的最大值.

例7正项等比数列{an}中，若a4+a3-2a2-2a1=6，则a5+a6最小值.

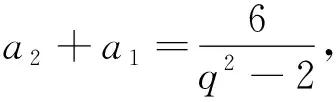
(2) 关于等比数列前n项积最值、等比数列中几项和最值问题.通过例题可以看出，在使用函数思想解题时，前提条件是要求出等比数列的首项a1与公比q或者已知条件来表达所要求解的问题.需要学生牢固的掌握等比数列与等差数列的性质，例如：等差数列：若p+q=s+t，则ap+aq=as+at.(p，q，s，t∈N*)、等比数列：若p+q=s+t，则apaq=asat.(p，q，s，t∈N*)、等比中项与等差中项等.

总而言之，函数思想是以函数为载体，把所求问题的条件，以函数的角度观察，利用函数性质，解决所求问题.数列是以正整数集为定义域的函数.在使用函数思想之前，掌握数列的各种性质，才能灵活的使用函数思想、创造性的解题.