基于深度学习的初中数学课堂教学问题链设计与实践——以浙教版八下“方差与标准差”为例

傅兰英

(浙江省杭州市西湖区教育发展研究院，浙江杭州，310020)

“学，源于思，始于问.”问题是知识的源泉，是智慧的摇篮. 在课堂教学中，问题贯穿整个课堂，问题的质量很大程度上影响学生素养的培育和思维的发展，要在教学中落实思维，实现深度学习. 下面以浙教版八年级下册第三章“方差与标准差”为例，说明如何利用问题链引导学生构造一个统计量，引导学生体会统计的思想，帮助学生建立统计观念.

1 分析内容，构建整体教学问题链

数据的分析是“统计与概率”板块中的重要内容，涉及分析数据的集中趋势和离散程度的常用方法，《义务教育数学课程标准(2011年版)》中对“方差与标准差”一节的目标要求是：体会刻画数据离散程度的意义，会计算简单数据的方差. 在此之前，学生已经学习了反映数据集中程度的统计量(平均数、众数、中位数)，会描述一组数的集中趋势，而“各数据之间的差异情况如何？”“如何用数学的方法进行描述？”也是实际问题中值得研究的问题. 因此确定本节课教学的问题链(关键问题)：如何反映数据的离散程度；如何定量刻画一组数据的稳定性；如何运用统计量解决问题.

图1

2 设计流程，突破统计教学关键点

基于以上的分析，在教学中引导学生思辨、分析、决策、审视获得构造统计量的方法，即通过创设情境，提出问题(如何反映数据的离散程度)；定量刻画，解决问题(确定参照基准→刻画数据偏离平均数的程度→修正样本容量不同对结果的影响)；合理规划，应用方法(解决实际问题)；梳理总结，类比迁移(归纳构造统计量的方法)四个步骤，提升学生学科素养.

2.1 思辨：创设情境，提出问题

为了让学生接受学习反映数据离散程度的统计量的意义，本环节将通过设置问题情境，让学生体会到已学的统计量(平均数、中位数、众数)无法解决新问题，引发认知冲突.引导学生观察数据的离散程度，即研究数据的波动程度，进而提出关键问题：如何反映数据的离散程度？提出解决问题的方案，突出用新的特征数来解决问题的必要性.

问题1：甲、乙两名射击手的测试成绩统计如下，现要挑选一名射击手参加比赛，你认为挑选哪一位比较适宜？为什么？

表1

追问1：你会先计算哪些特征数？结果如何？

追问2：如果要选择发挥更稳定的选手，应该怎么选？

追问3：有什么方法来判断两组数据的稳定性？

2.2 分析：定量刻画，解决问题

要研究一组数据波动大小可以从定性、定量两个角度进行，若是定性则可以利用折线统计图直观地呈现结果；若是定量则需要引入新的特征数，用于反映一组数据的离散程度，即解决“如何定量刻画一组数据的稳定性？”这一问题. 本环节通过三个探究(如何确定参照基准→如何刻画数据偏离平均数的程度→如何避免样本容量不同对结果的影响)，让学生完整经历方差概念和计算公式探究的全过程，对知识有更深刻的理解，并在不断启发学生思考的过程中，培育了学生的高阶数学思维和学科素养.

探究一：如何确定参照基准

学生在构造一个统计量的过程中，即探究数据的波动程度时，通常想到求“极差”(最大值-最小值)的方法，引导学生明确极差仅反映这组数据中两个极端值的离散程度，没有充分利用所有数据，不具有普遍性，让学生进一步探究.

问题2：通过计算我们发现平均数、中位数、众数无法刻画数据的离散程度，但能否通过这三个特征数来反映数据的波动情况？

追问1：为考虑所有数据的波动程度，你认为将哪个量作为波动时的参照基准较合适？

追问2：回忆平均数、中位数、众数的意义，思考刻画一组数据的稳定性时，应选择哪个量为参照基准？

探究二：如何刻画数据偏离平均数的程度

通过分析，学生选择合适的统计量(平均数)作为反映一组数据上下波动程度的参照基准.针对如何刻画数据偏离平均数的程度，在探究过程中让学生小组合作，思维碰撞，对不同方式进行比较和修正.

问题3：如何刻画一个数据偏离其平均数的程度？

追问1：如何刻画一组数据偏离其平均数的程度？

追问2：分析比较结果你发现了什么问题？如何修正你的计算方法？

学生通过问题链思考，尝试计算一组数据与平均数做差来刻画离散程度，分析思路并不断修正计算方案. 为消除正负抵消的影响，学生会再尝试以下方式：①将所得的差加上绝对值、求和；②将所得的差平方、求和. 以上两种方法如何取舍，教师需要进一步引导，接着通过以下的原题变式来实现.

问题4：原题变式为“增加甲、乙第六次和第七次成绩的数据”，以上算法能否客观地比较两组数据的稳定性？

表2

追问：根据前面结论(偏差的绝对值之和、偏差的平方之和)计算，是否都能反映数据的波动程度？

学生通过计算发现计算偏差的绝对值之和某些情况下无法反映数据的波动程度，而偏差的平方之和使原本较小的差距拉大，更精确地刻画数据稳定性大小，为后续继续探究做铺垫.

探究三：如何避免样本容量不同对结果的影响

在探究过程中，学生会进一步考虑样本容量对数据计算的影响. 教师通过原问题变式与学生一起探索和修正计算方法.

问题5：原题变式为“增加甲第六次和第七次成绩，乙不变”，以上算法能否客观地比较两组数据的稳定性？

表3

追问：还可以怎么来修正你的计算方法？

通过原问题的再次变式，探究数据个数对偏差的平方之和造成影响，得出结论：避免影响产生的解决方法是取结果的平均数(偏差平方的平均数)，进一步修正了计算方案，从而获得方差的概念、计算公式和意义.

问题6：利用方差的知识解决下列练习.

练习1：为了考察甲、乙两种小麦的长势，分别从中抽出10株苗，测得苗高如下(单位：cm)，请问哪种小麦长得比较整齐？

甲：12，13，14，15，10，16，13，11，15，11；

乙：11，16，17，14，13，19， 6， 8，10，16.

追问1：在比较两组数据的离散程度时，一定要平均数相同吗？

追问2：方差的单位是什么？怎么设计一个统计量令它具有实际意义？

通过练习帮助学生巩固方差计算公式的运用，在理解方差意义的基础上，进一步让学生理解考察一组数据离散程度的必要性. 并顺势得到标准差的概念，并指出标准差也是反映数据的离散程度的. 并用以下两个针对练习巩固方差与标准差的概念.

2.3 决策：合理规划，应用方法

基于已学的各类统计量以及对它们含义的理解基础，进而设置综合性习题进行知识巩固，让学生感受“如何运用统计量解决问题？”实现学生对统计概念更全面地认识，培养灵活运用知识解决问题的能力. 通过练习2将学习过的统计量进行复习，让学生熟练运用知识解决问题，重点探究从不同的角度分析问题时，要选取不同的统计量，体现各统计量的不同意义.

练习2：甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示：

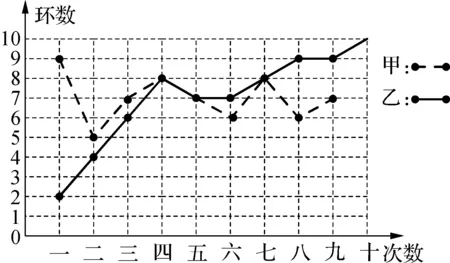
图2

(1) 填写下表：

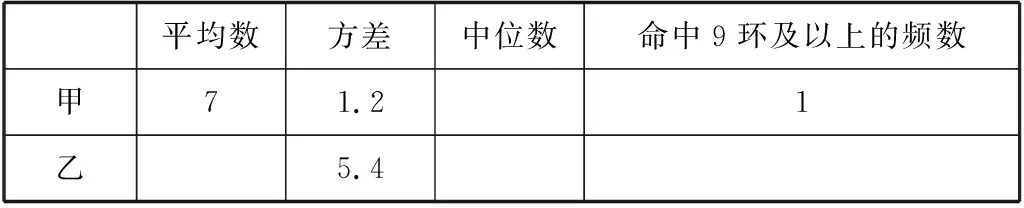
表4

(2) 请从下列四个不同的角度，结合不同的统计量对这次测试结果进行分析：①谁的成绩更稳定？②谁的总体成绩好些？③谁得高分的机会大？④分析谁更有潜力？

2.4 审视：梳理总结，类比迁移

课堂总结时，利用问题链带领学生回顾本节课方差概念的形成过程：

①为什么要学习方差？

②在引入方差的过程中为什么要与平均数作差？

③为什么取偏差的平方，不取绝对值？

④为什么在求出各偏差的平方后，要除以n？

⑤方差与标准差之间有什么联系和区别？

⑥方差与标准差能反映一组数据的什么特性？

理解方差的意义和作用，梳理构造一个统计量(方差)的过程，即知识结构图，形成统计的一般观念，为后续学习更复杂的统计内容做好铺垫，培养学生类比迁移的能力.

3 反思成效，寻求认知结构延伸区

科学教育的目的是培养知情的决策者，使学生具有进行正确决策的知识基础和能力.基于关键问题为导向，以问题链为各教学活动环节的载体是初中数学教学研究的新思路，通过观察，发现，质疑、思考的过程，引发认知冲突，主动探究知识的建构路径，促进知识的动态生成，为深度学习的理解与运用寻找到一个有效的突破口，它可以激发学生学习的内在动力，调动深度思考的热情，进而由浅入深挖掘知识的联系，打开认知结构延伸区，形成提出问题、分析问题、解决问题的习惯，逐步培养良好的思维方式，培养学生数据分析观念.