基于直观想象的解析几何“几何条件代数化”策略探析

周 宁,林新建

(1. 福建师范大学附属福清德旺中学，福建福清，350319 2. 福清市教师进修学校，福建福清，350300)

在高三数学复习中，学生对解析几何的主要印象是运算量大、复杂，因此始终抱有畏难情绪，卷面上经常出现“一设二联立三韦达四放弃”.问题的根源在于对解析几何基本思想的理解出现了偏差，片面认为解析几何就是算，缺少对问题的几何思考.解析几何的基本思想是坐标法，但是坐标法并不等同于代数运算，它的运算带有几何的特征[1].因此教学中要引导学生用几何的眼光去看解析几何问题，几何直观与代数推理并进，探索简洁的几何问题代数化途径，从而提高运算效率，化解解析几何问题的难点.

基于以上的认识，笔者整合教材及高考相关资源，设计一节高三微专题复习课“基于直观想象的解析几何‘几何条件代数化’策略探析”.

1 教学过程设计

1.1 数学情境，感知“几何条件代数化”背景

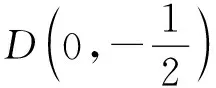
思考1：你如何求解这个问题？一般的步骤与过程是什么？

生：(预设)从问题解决过程进行说明：设直线l的方程与点A，B坐标，联立直线与抛物线方程得到一元二次方程，利用韦达定理得到A，B坐标关系……

思考2：在问题1的解决中，点与直线的坐标化很轻松完成，问题解决的关键是如何对“点D与以线段AB为直径的圆的位置关系”这个几何条件进行代数化.大家有哪些想法呢？

设计意图：通过“点与圆的位置关系”让学生体会解析几何解决问题的手段就是将几何问题进行代数化，并意识到解决问题的关键在于题意中几何条件的代数化.

1.2 数学探究，抽象“几何条件代数化”特征

生：(预设)

①写出圆的方程，将D的坐标代入圆方程的左边，判断所得代数式的符号；

②计算D与圆心的距离，与半径比较大小；

③转化为“判断∠ADB是锐角，直角还是钝角”.

追问1：比较上述想法，哪种操作性更强？为什么？

生：选择③.直观上感觉①②代数化得到的结构会比较复杂，①需要写出圆的方程，②需要计算两个长度.

追问2：如何对想法③进行代数化？

追问3：不妨设A(x1，y1)，B(x2，y2)，请大家对上述3种想法进行代数化表达，判断刚才的直观想法是否正确.

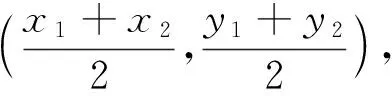
设计意图：让学生通过对思考2及追问的思考理解要实现几何条件的代数化，关键在于对“几何条件”特征的认知，并初步感受到不同的认知会对后续的运算复杂程度产生不同的影响，为“数学内化，辨析‘几何条件代数化’内涵”作好铺垫.

1.3 数学体悟，概括“几何条件代数化”要义

思考3：上述过程我们是如何将几何条件代数化？

生：如果现有的几何条件已经具有明显的代数特征，可以直接代数化.还可以对已有的几何条件挖掘相关的几何性质，再进行代数化.

师：解析几何，顾名思义，对“几何问题”进行解析，通过代数运算和推理研究几何图形.解析几何问题解决的三步曲：

图1

其中，首要的问题是将几何图形的要素和特征进行坐标化，问题的难点在于几何特征如何进行代数化.从问题1的解决过程我们可以看出转化的过程大致是：几何问题→(几何性质)→代数问题.对于几何条件性质的挖掘如果比较充分，得到的几何特征代数化的形式比较简洁.

思考4：你能挖掘以下常见几何条件的几何性质吗？

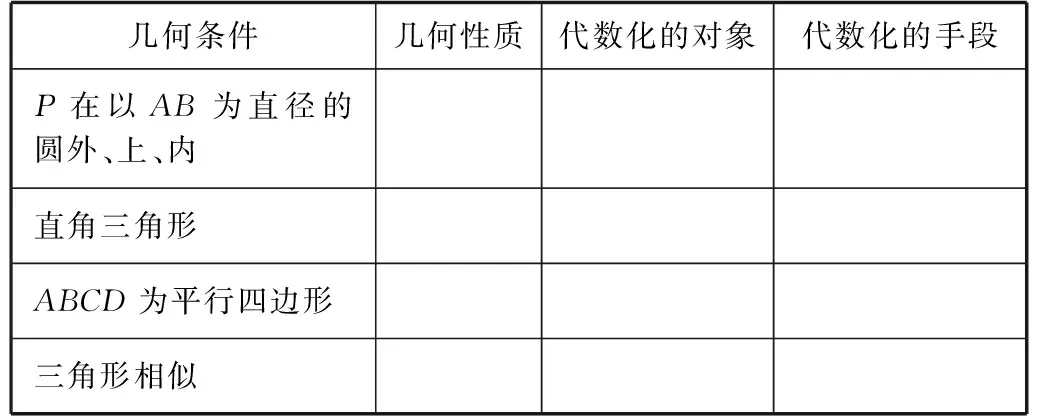
表1

追问：通过上述表格，我们可以发现，我们代数化的常见对象就是长度、角度，在实际问题解决中还会遇到面积，那么针对这三个对象我们的代数化手段有哪些呢？

生：长度的代数化的手段有两点距离公式、向量的模、直线参数方程t的几何意义；角度的代数化手段有斜率、向量夹角；面积的代数化手段有三角形面积公式.

设计意图：让学生将前面的认知进行一个总结，明确代数化的策略，意识到图形及几何性质的重要性.通过思考4学生感受到几何问题可以挖掘不同的几何性质，进而思考如何选择几何性质进行代数化表达.学生的初步感受是与代数化的对象有关，为下一步“辨析内涵”埋下伏笔.

1.4 数学内化，辨析“几何条件代数化”内涵

师：通过上述的分析，我们知道，几何条件代数化的关键就是对几何条件挖掘相关的几何性质，得到对应的代数特征，用坐标代入实现代数化.现在我们再来体会一下几何条件代数化过程.

思考5：你的结论是什么？为什么？

生：直线PB与圆Q是相切的.

思考6：那么你对几何关系“直线PB与圆Q相切”有哪些代数化的手段呢？

学生活动：(预设)

设A(x1，y1)，B(x2，y2)，

解法一：(几何转化)圆心到直线的距离等于半径→点Q到直线PA，PB的距离相等.

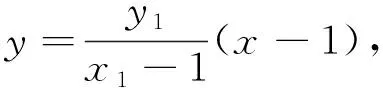
解法二：点Q到直线PA，PB的距离相等⟺∠APQ=∠BPQ.

(数量)视角1 角→斜率

∠APQ=∠BPQ⟺tan ∠APQ=tan ∠BPQ，

又∵kPA=tan ∠APQ，kPB=tan (π-∠BPQ)=-tan ∠BPQ，

视角2 角→向量夹角

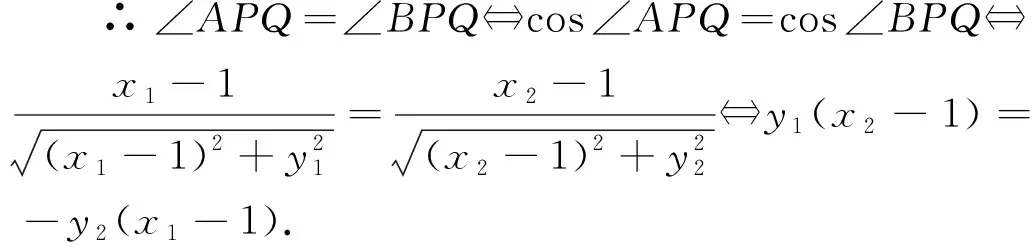
思考7：回顾上述几种解法，能说说你对几何条件代数化途径的认识吗？

生：可以从数与形两个方向切入，要结合图形去挖掘几何性质，或根据数的关系去发现对应图形的几何性质.

师：不同方向得到初始的代数化结构不同，有的复杂，有的简单，但最终运算化简得到的代数结构是相同的.不同的选择，运算的复杂程度不一样，具体哪种选择更优，取决于对应代数特征的代数化表达.需要注意的是，这个表达一定要结合图形去判断，例如，线段的表达一定是复杂的吗？一定是用距离公式表达吗？

设计意图：让学生通过对问题2图形几何性质的不同层次和方向的挖掘体会到不同几何性质得到的初始代数结构不同，并明确要结合图形进行策略上的选择.

1.5 数学应用，深化“几何条件代数化”理解

图2

(1) 求动点P的轨迹方程.

(2) 设直线PA和BP分别与直线x=3交于点M、N，问：是否存在点P，使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，请说明理由.

思考8：“△PAB与△PMN的面积相等”如何进行代数化会使得结构较为简单？

思考9：能否进一步挖掘问题的几何性质？

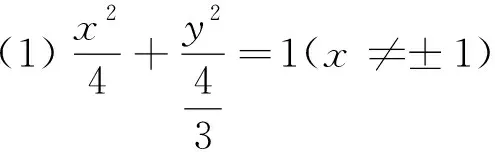
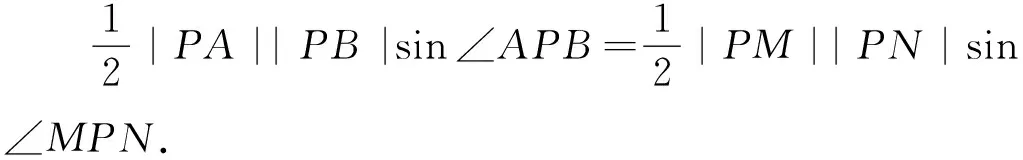
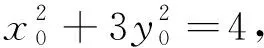
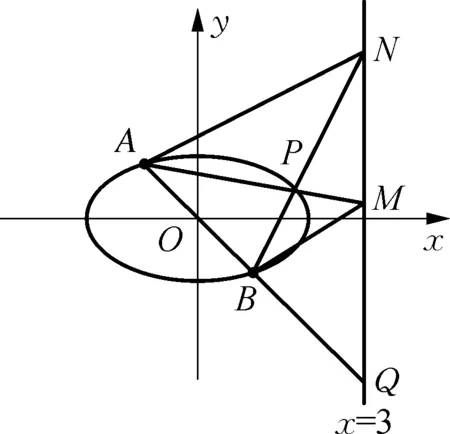
图3

解法2：如图3，连接AN，BM，延长AB交NM于点Q.

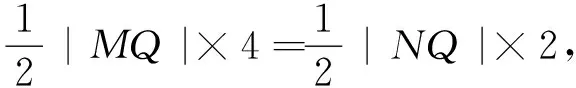
同理知B是线段AQ的中点，则AM，BN是ANQ的中线，故点P是△ANQ的重心.

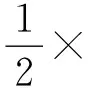
课堂小结：

思考10：通过本节课的学习，你对“几何条件代数化”有什么体会？

生(预设)：对于解析几何问题，要先用几何眼光观察与思考，要重视对图形几何性质的挖掘，结合图形判断哪一种几何性质的代数化表达会比较简洁，再用坐标法解决.

板书设计：

图4

2 教学反思

解析几何问题本质上是“几何问题”，对几何对象的思考应放在首位，也就是要有“先用几何眼光观察与思考，发现与挖掘图形的几何性质，再用坐标法解决”的意识，使几何直观成为分析问题、解决问题的利器.

2.1 几何直观的理解是解几问题解决的前提

解析几何问题代数化的策略上就是从数、形两个方向思考，若只从代数角度去认识，就可能造成问题的代数化表达比较困难或结构复杂，因而需要图形的支撑.通过分析几何图形的要素及其性质，借助“形”的直观思考“数”的表达，结合图形的几何特征感知数量关系及本质属性，有助于学生理解问题，寻求问题解决的思路.正如问题2中，学生通过“形”(直线与圆相切)到“数”(点到直线的距离)再到“形”(角相等)一系列的过程感受到“数”“形”之间的转化，尤其是对“形”(角相等)进一步的思考，又可以得到“数”(斜率关系)或基于“形”(三角形相似、角平分线)得到“数”(线段关系)或基于“形”(对称)得到“数”(点坐标关系)等.这些“形”“数”关系的转化依赖于学生对“形”的直观理解水平，不同水平影响问题解决.

2.2 直观想象的提升需几何活动经验的积累

学生几何活动经验的体验和积累是直观想象素养获得和提升的有效途径.设计有效的活动，让学生有充裕的时间思考，多角度去探索、挖掘图形的几何性质，理解“形”的代数表达，同时在积累中获得对常见几何图形性质的经验，再根据情境进行合理的选择，体会解析几何问题的研究思路、方法和思维.

总之，解析几何教学不只是要培养数学运算能力，更为重要的是要提高学生的几何直观能力，提升直观想象素养.