含电动汽车和智能软开关的配电网动态重构

2022-10-15林文键朱振山温步瀛

电力自动化设备 2022年10期

林文键，朱振山，2，温步瀛

（1. 福州大学电气工程与自动化学院，福建福州 350108；2. 智能配电网装备福建省高校工程研究中心，福建福州 350108）

0 引言

配电网是电能从生产者到消费者之间传输的最终环节，对能源经济的发展有重大影响。现行的配电网存在以下问题：分布式能源（DG）的接入使配电网的潮流双向流动，线路损耗更加复杂且难以控制，这给配电网的经济运行带来影响［1］；电动汽车（EV）的普及使得负荷侧呈现出较强的随机性和波动性，降低了配电网的电压质量。

传统配电网仅通过配电网重构（DNR）提高配电系统的可靠性和经济性［2］。DNR 是指通过改变配电系统的开关组合寻求更好的网络运行拓扑，从而改善节点电压以及降低网损。DNR 方法主要分为静态重构和动态重构2 种。静态重构［3］在进行DNR 时仅考虑单一时间断面，假定整个时段的负荷恒定不变，局限性较大；动态重构［4］是对一段时间内的配电网架构进行动态优化，以提升网络的灵活性。实际配电网的负荷总是不断变化的，动态重构更能应对网络的复杂性。

同时，由于EV的接入会加剧配电网末端节点的电压降落以及增大网损［5-6］，为减轻EV 充电的随机性对配电网运行稳定性和经济性的影响，需对EV充电负荷进行有序调度。文献［7］提出“延时”和“错峰”2 种充电策略，对EV 无序充电负荷进行引导，但这2 种策略针对的均是EV 集群，不能实现EV 的分散式调度，存在较大的误差。文献［8］提出拉格朗日分散式优化方法，但其对于需求响应采用的是固定分时电价策略，不能实时响应电网的负荷波动。文献［9］提出虚拟电价理论，可结合配电网的基础负荷制定实时电价，用于提升EV负荷错峰填谷的效果。

近几年，电力电子器件的发展为打破传统配电网的物理结构提供了新的思路，以智能软开关（SOP）［10］为代表的电力电子柔性互联器件，可用于代替传统的配电网物理开关，起到提升配电系统运行经济性和可靠性的作用。文献［11］提出SOP接入位置和接入数量的不同会对网络的灵活性和经济性产生较大的影响。文献［12］提出需求响应和SOP的协同优化可以减少配电网的运行成本。现有关于SOP 应用的研究主要关注配电网的优化运行方面［13-14］，而较少以SOP代替DNR时的联络开关。SOP在DNR 时代替联络开关，可以起到控制线路潮流和电压水平的作用，从而增加配电网的灵活性。

目前，已有一些研究关注EV有序调度在配电网中的应用［15］，但较少有研究应用拉格朗日分散式优化方法进行EV调度，且一般采用固定分时电价策略来引导EV 的有序调度，EV 负荷的错峰填谷效果较差。此外，现有关于EV 调度的研究均未考虑与SOP和DNR 的联合优化运行，不能充分发挥配电网灵活调节的能力。

综上，本文在新能源接入的背景下，提出综合考虑EV 和SOP 的多时段DNR 策略，有效利用EV 的有序调度和SOP 灵活控制潮流的特性，进一步降低DNR 费用，提高新能源的消纳率。在算法方面，提出基于拉格朗日松弛分散式优化方法和虚拟电价对EV 进行有序调度，将包含DG、EV 和SOP 的配电网动态重构模型转化为混合整数二阶锥规划（MISOCP）问题进行求解。为提升求解速度，在DNR 模型中加入3类加速条件。为验证本文所提方法对于DNR经济性和电压幅值的提升作用，在MATLAB 中采用CPLEX求解器进行算例仿真分析。

1 EV调度模型

本文采用拉格朗日松弛分散式优化方法和虚拟电价相结合的方法对EV 进行调度。拉格朗日松弛分散式优化方法可以实现对每辆EV 的充电优化。以虚拟电价代替固定分时电价可实现与电网负荷的实时匹配，但虚拟电价本身不作为电价的真实结算标准，仅用于根据电网负荷引导EV 负荷实现错峰填谷。

1.1 EV充电负荷基础模型

假定在充电结束时EV电量可达到其期望值，且每辆EV 均愿服从充电调度。从出行需求角度考虑EV 到达目的地时是否需要充电，以预测每辆EV 的充电时段分布，得到预测的无序EV负荷［8］。

1）EV用户的行驶里程。

每辆EV 上下班的行驶里程分布用对数概率密度函数fm(·)表示，如式（1）所示。

式中：tw、th分别为EV 到达单位和回到住宅的时间；期望μw=8.5；期望μh=17.5；标准差σs=0.5。

3）初始荷电状态（SOC）。

根据实际情况，假定EV电量在上班之前都满足车主出行的最低电量要求，数学模型为：

式中：SRd为EV 从单位（住宅）到住宅（单位）单程所需SOC；Sd1为1 km所消耗的SOC。

根据EV 的单程行驶距离，为考虑每辆EV 初始SOC的差异，可将EV的初始SOC表示为：

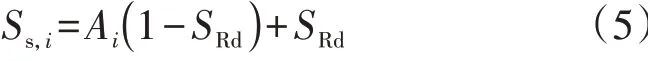
式中：Ss，i为第i辆EV 的初始SOC；Ai为N维（0，1）取值随机行向量中的第i个值，N为EV数量。

对于已知初始SOC 和上下班单程距离的EV，首先应判断该EV 在到达单位或回到住宅后是否具有充电需求：若到达单位或回到住宅后EV的SOC满足式（6），则为保证EV电量可以满足出行要求，需对该EV进行充电。

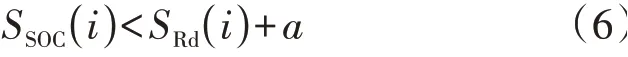
式中：SSOC(i)为第i辆EV 到达单位或回到住宅时的SOC；SRd(i)为第i辆EV 单程所需SOC；a为很小的常数，用于模拟电池的自放电。假设符合式（6）的EV均服从优化调度，且其充电需求均能被满足。

1.2 基于虚拟电价的EV充电调度

本文设定虚拟电价［9］的调度周期T=24 h，将调度周期离散成若干等长的时段，每个时段的时长ΔT=0.25 h。虚拟电价和配电网基础负荷的关系为：

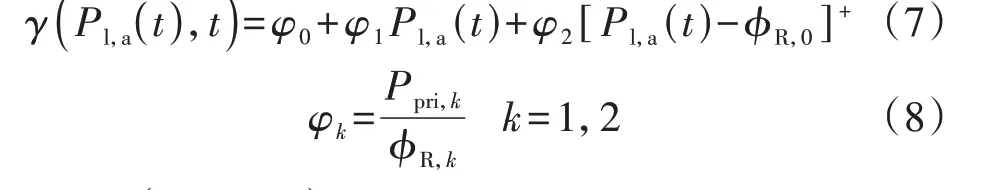
式中：γ(Pl，a(t)，t)为EV 接入时刻t的虚拟电价，Pl，a(t)为t时刻接入配电网的总负荷，如式（9）所示；φ0、φ1、φ2为制定虚拟电价时的调整系数，为使虚拟电价与现行的峰谷电价处于同一比例金额，令φ0=-0.21元／（kW·h）；φR，0为负荷基准值；[·]+表示max{0，·}；k取值1、2 分别表示峰时段、谷时段，Ppri，1、Ppri，2分别为峰时段、谷时段电价，φR，1、φR，2分别为峰时段、谷时段负荷均值。对式（7）求负荷的偏导，可得φ1≥0，因此总体上虚拟电价与当前负荷水平呈正相关性，φ2的设置是为了使总负荷大于负荷基准值时的虚拟电价有一个更大的提升。

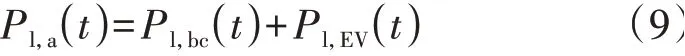
式中：Pl，bc(t)为t时刻的基础负荷；Pl，EV(t)为t时刻接入配电网的EV负荷。

1.3 拉格朗日松弛分散式优化

1.3.1 集中式模型

集中式优化调度的目标函数设定为在满足EV用电需求的前提下EV的充电费用F最小，即：

式中：Se，i为第i辆EV 的期望SOC；Cc为电池容量；η为充电效率。

2）EV可调度时间约束［16］。

设定EV 仅在接入时段末和离开时段的前一个时段末接受虚拟电价的调度，因此有：

式中：Pl，m为配电网所能承受的最大负荷。

1.3.2 拉格朗日松弛分散式优化模型

1.3.1 节的优化模型是针对集中式优化方法的，本文采用拉格朗日松弛分散式优化方法将集中式模型转化为分散式模型。算法流程图［17］如图1 所示。图中：ξ为约束条件数；λ（v）为第v次迭代的拉格朗日乘子；α(v)为第v次迭代的步长；h(x(v))为第v次迭代对应的次梯度与该次梯度对应的1范数的比值。

图1 拉格朗日松弛法的一般流程图Fig.1 General flowchart of Lagrange relaxation method

根据图1，将集中式优化模型转化为分散式模型的步骤如下。

1）目标函数不变，仍为1.3.1节式（10）。

式中：λt为t时刻的拉格朗日乘子。可再将式（15）分解为针对每辆EV的子问题，如式（16）所示。

4）原问题与对偶问题的解。

将步骤2）中求得的Jt i代入原问题和对偶问题。若求得的原问题和对偶问题目标函数的差值满足精度要求，则可近似认为对偶问题的解即为原问题的解；否则，对λt进行更新。

5）采用次梯度法对λt进行更新。

由于对偶问题是非光滑的，因此采用次梯度法。次梯度法是从一个初值出发，沿着次梯度的方向进行迭代，设k为迭代次数，k=1时先给λt一个初值，迭代公式为：

式中：ε为拉格朗日乘子的迭代率。此时对偶问题的下确界为原问题的最优解，迭代结束。

2 DNR的MISOCP模型

本文对于配电网运行优化的研究分为2 个阶段：第1 阶段根据配电网提供的基础负荷信息制定虚拟电价，再通过拉格朗日松弛分散式优化方法和虚拟电价实现EV 负荷的有序调度；第2 阶段根据制定的EV 充电计划以及配电网节点的区域划分和负荷分配，将EV负荷接入配电网，在风、光等清洁能源接入的背景下，建立含EV和SOP的多时段配电网优化重构模型，提升配电网运行的经济性和电压水平。对于模型中存在的非线性约束，采用二阶锥松弛和大M法进行线性转化。

2.1 DNR的目标函数

本文提出的模型以弃风惩罚、弃光惩罚、网损费用、SOP 损耗费用和开关动作费用之和最小为目标函数，即：

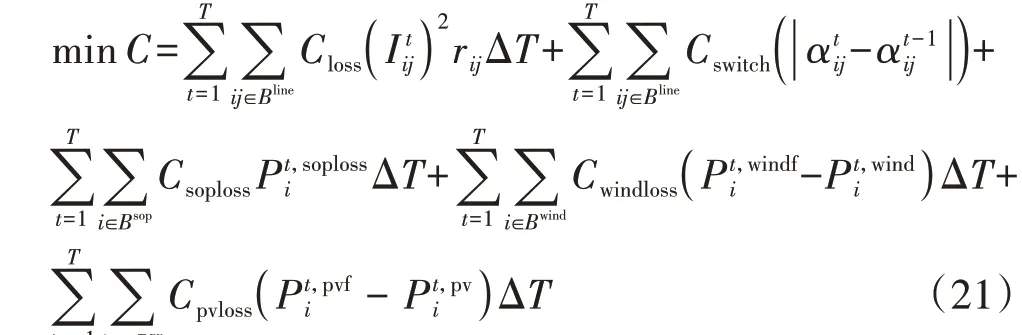
式中：C为DNR 模型的总费用；Bline为配电网中含联络线的所有支路集合；Bsop为配电网中接入SOP的节点集合；Bwind为配电网中接入风电机组的节点集合；Bpv为配电网中接入光伏的节点集合；Closs、Cswitch、Csoploss、Cwindloss、Cpvloss分别为网损费用系数、开关动作费用系数、SOP 运行费用系数、弃风费用系数和弃光费用系数；It ij为t时刻流经支路ij的电流；αtij为支路ij的开闭状态，是0-1变量，其值为0时表示t时刻支路ij断开，为1时表示t时刻支路ij闭合；Pt，soplossi为t时刻SOP 接入节点i上换流器的损耗；Pt，windfi和Pt，pvfi分别为t时刻风电接入节点和光伏接入节点发出的有功功率；Pt，windi和Pt，pvi分别为t时刻风电机组节点和光伏节点接入电网的实际功率。

2.2 约束条件

1）DistFlow潮流约束。

DistFlow［18］是一种以支路功率为研究对象的潮流模型，本文所用的DNR的DistFlow潮流模型为：

式中：Bn为配电网中所有节点的集合；Bf为配电网中根节点的集合；Nn和Nf分别为所有节点数和所有根节点数。

为减少开关状态的寻优时间，本文对开关状态进行相关约束［19］。根据IEEE 33 节点系统的拓扑特点，将支路分为不在环中的“树状支路”和在环中的“环状分支”2 种。在满足配电网辐射状且无孤岛运行的要求下，增加3 种“加速性约束”：放射型支路全部闭合；非环状分支路集合至多有1 条支路断开；环状支路集合至少有1条支路断开。

3）开关动作次数约束。

为了保证开关在使用周期内正常运行，减少开关动作对开关使用寿命的影响，保证配电网运行的经济性，需要对开关动作次数进行限制，即：

6）DG出力模型。

对于DG 的建模，本文考虑风电和光伏出力的特点不同，设置不同的出力上限来限制DG 的出力，不考虑DG出力的不确定性，模型为：

8）ESS模型。

ESS 的设置可以起到平缓常规发电机出力以及提升风、光出力的作用，因此配电网中需加上ESS。但ESS 需满足多时段的约束限制，ESS 的存在会使DNR过程中存在时间上的耦合，约束如下。

（1）充放电状态约束，即：

2.3 优化流程

本文的优化调度流程图如图2所示。

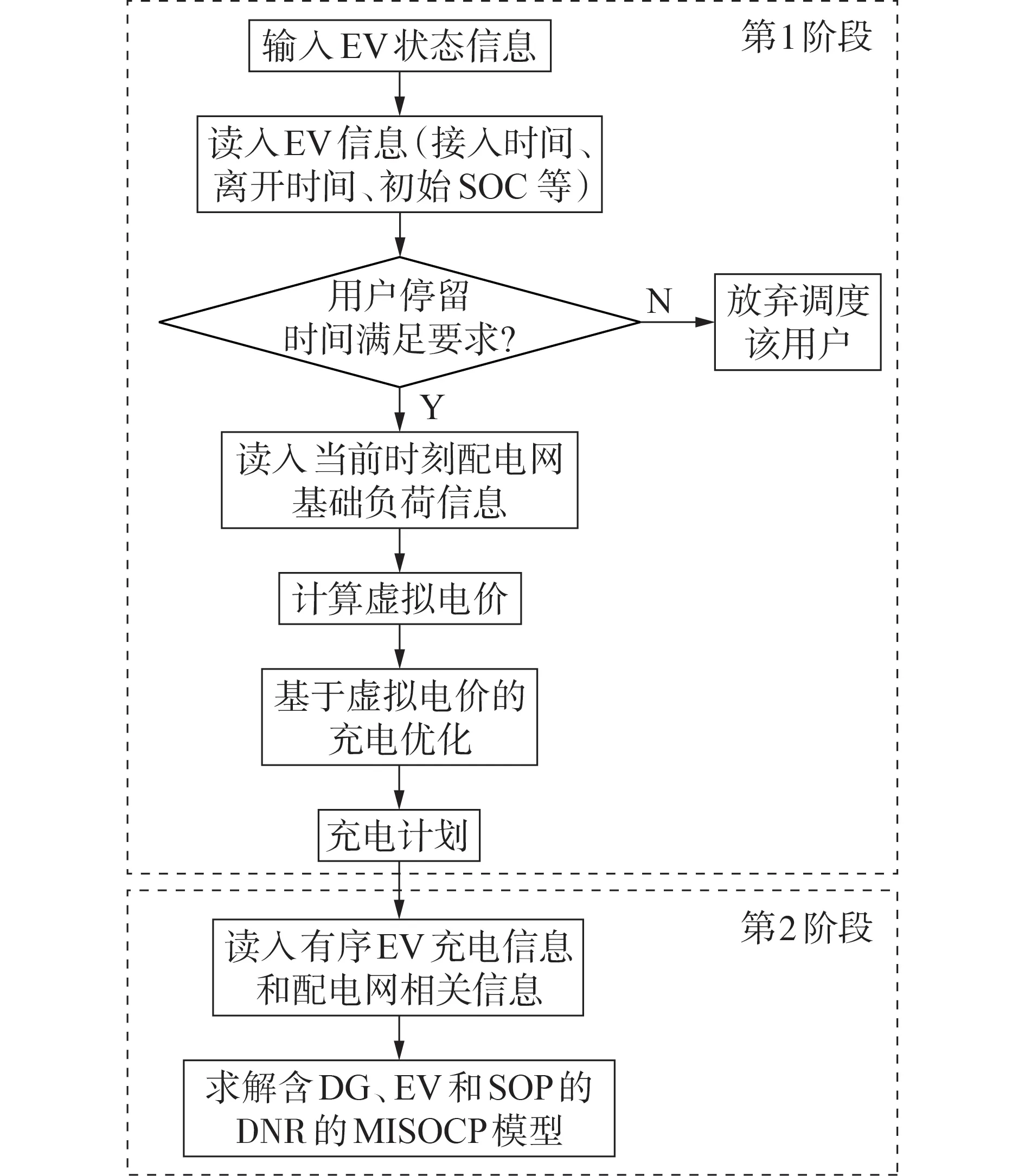
图2 优化调度流程图Fig.2 Flowchart of optimal scheduling

3 仿真和优化

3.1 EV优化分析与负荷分配

设置配电网一天内服务的EV数量为100辆，EV电池容量为30 kW·h，额定充电功率为10 kW，充电效率为0.9，EV 充电后离开的期望SOC 均为0.9。通过判定EV 早晚出行到达目的地后的SOC 是否满足下一次出行要求来确定EV是否需要充电。

附录A 图A1 为配电网基础负荷叠加无序EV 充电负荷示意图。由图可以看出，无序充电的EV车主充电习惯与生活用电习惯有重叠部分，这造成配电网负荷峰值进一步提升，出现“峰上加峰”的现象，而通过与配电网负荷匹配的动态虚拟电价调度之后，有序EV负荷接入配电网改变了高峰时段EV车主的充电习惯，将高峰时段的负荷转移到了低谷时段，起到了较好的填谷作用，如附录A 图A2配电网基础负荷叠加有序EV充电负荷示意图所示。

在提取出无序充电的EV 负荷和有序充电的EV负荷数据后，对配电网的区域划分进行改进，将配电网分为商业区、办公区和住宅区。假设：白天时，80%的EV 车主出行到办公区，15%的EV 车主出行到商业区，5%的EV 车主留在住宅；傍晚时，95%的EV车主回到住宅区，5%的EV车主留在办公区。无序充电的EV负荷和有序充电的EV负荷均按照该规律进行负荷分配。配电网的区域划分图如附录B 图B1所示。

3.2 SOP接入对配电网的影响

3.2.1 SOP接入位置和接入数量分析

对于DNR 模型，本文通过二阶锥松弛将模型转化为可用求解器CPLEX 求解的MISOCP 问题。配电网的额定电压为12.66 kV，基准容量为10 MW，母线0为根节点，电压为1.00 p.u.，为维持配电网的电压稳定，设定电压最小值为0.95 p.u.，最大值为1.05 p.u.。在节点19 和节点32 接入ESS。DNR 的目标函数中网损费用系数、开关动作费用系数、SOP 运行费用系数、弃风费用系数和弃光费用系数分别取为400元／（MW·h）［20］、2元／次［20］、400元／（MW·h）［21］、400 元／（MW·h）［22］和400 元／（MW·h）［22］。在联络线支路涉及的节点接入容量为1 MW 的SOP。在节点11 和节点24 接入风电机组，在节点17 和节点21接入光伏电站，所有DG 均为恒功率因数发电，功率因数为0.95，DG出力曲线如附录C图C1所示。

在无EV 接入时，设置如下5 个场景来分析SOP对DNR 的影响：场景1，未接入SOP 的DNR；场景2，线路8-14 接入SOP 的DNR；场景3，线路11-21 接入SOP 的DNR；场景4，线路8-14 和线路11-21 接入SOP 的DNR；场景5，线路8-14、线路11-21 和线路17-32 接入SOP 的DNR。DG 渗透率均为40%。

各场景下的DNR运行费用如表1所示。由表可知：渗透率为40%时DG 可以被配电网完全消纳；与场景1 相比，场景2 的网损费用减少23.46%，SOP 费用增加24.63 元，总费用减少60.12 元；场景2 和场景3 在不同位置接入单一SOP 对配电网的运行经济性影响不同，但是相较于场景1，接入SOP 均会减少总费用和网损费用；与场景1 相比，场景4 的总费用减少69.28 元，网损费用减少26.21%，与场景3 相比，场景4 的总费用减少24.81 元，网损费用减少30.46元；与场景4 相比，虽然场景5 的SOP 运行费用增加12.39 元，但是网损费用减少47.63 元，总费用减少35.24元。

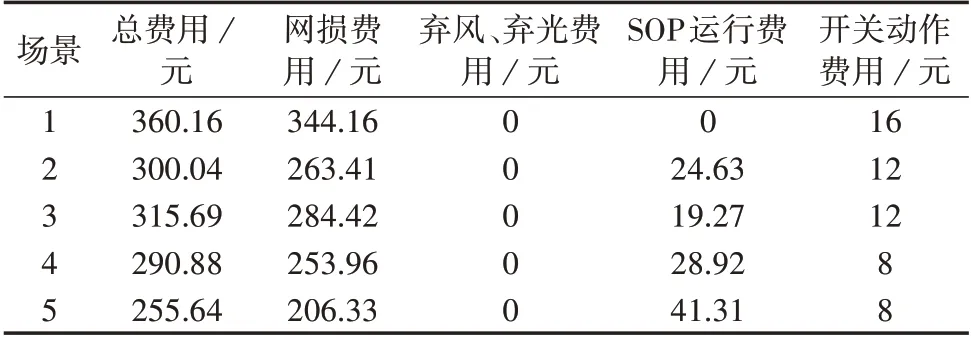
表1 无EV接入场景下DNR运行费用Table 1 DNR operation cost of scenarios without EVs

3.2.2 SOP对DNR节点电压的影响

为更好地体现SOP 维持电压的作用，选用19:00时各节点的电压。附录D 图D1 为未接入SOP 和接入单一SOP 的节点电压图。由图可以看出，接入SOP时DNR的电压质量更好。

3.3 EV接入分析

3.3.1 EV接入下SOP的作用分析

为分析EV接入时SOP在有序和无序EV充电模式下的作用，设置以下5 个场景：场景6，接入无序EV 和不接入SOP 的DNR；场景7，接入有序EV 和不接入SOP 的DNR；场景8，接入无序EV 和线路7-20接入SOP 的DNR；场景9，接入有序EV 和线路7-20接入SOP的DNR；场景10，接入有序EV和线路7-20、11-21接入SOP的DNR。DG渗透率均为40%。

各场景下的DNR运行费用如表2所示。由表可知：在接入无序EV 和有序EV 时40%渗透率的DG仍可以完全被配电网消纳；未接入SOP 时，对EV 进行有序调度之后再将其接入配电网中，可以在一定程度上减少总费用；若再接入SOP，则会更进一步减少总费用；配电网接入有序调度的EV 之后，再在线路7-20、11-21 接入SOP，会大幅减少网损费用，从而使总费用减少。

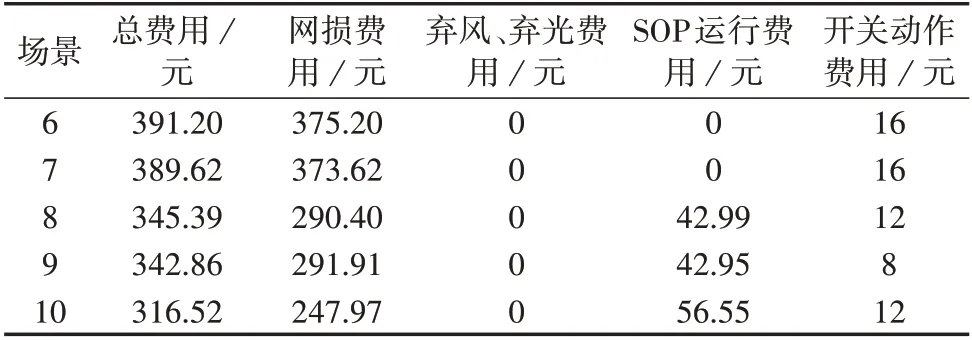
表2 有EV接入场景下的DNR运行费用Table 2 DNR operation cost of scenarios with EVs

3.3.2 EV和SOP接入下DG渗透率灵敏度分析

本节在线路8-14 接入单一SOP 和接入有序EV背景下进行算例仿真分析。表3 为不同DG 渗透率下的模型求解结果。

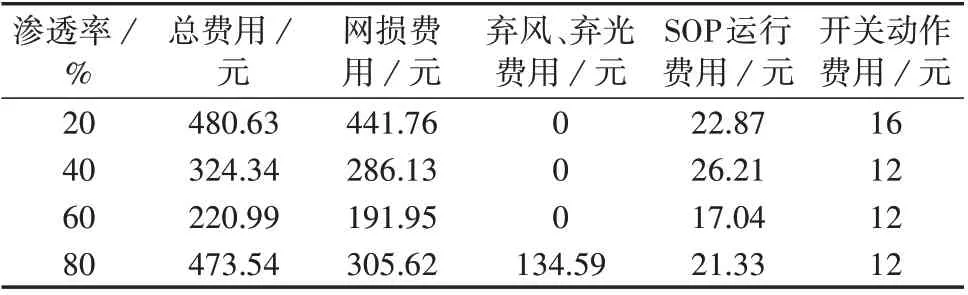
表3 不同DG渗透率下的模型求解结果Table 3 Model solution results under different permeabilities of DG

由表3 可知：DG 渗透率为20%时，DNR 总费用较高，这是由于此时虽然DG 完全被配电网消纳，但是还需要较多变电站节点出力，因此网损费用较高；DG 渗透率为40%和60%时，DG 出力完全被配电网消纳，由于负荷较多地利用较近的DG 出力，这使网损费用减少，从而使DNR 总费用减少；DG 渗透率提高到80%时，此时DG 出力无法完全被配电网消纳，网损费用增加，同时产生弃风、弃光费用，导致配电网总费用增加。