基于马尔可夫决策过程的电动汽车充电站能量管理策略

黄帅博，陈 蓓，高降宇

（上海工程技术大学 电子电气工程学院，上海 201620）

0 引言

全球工业化的加速和人类物质需求的提高，导致化石原料不断减少及其带来的环境问题日益凸显。有数据显示，2021 年全球能源的消耗量达到1.386 5×1010t 油当量，与此同时，化石燃料直接或间接地产生了3.368×1010t 的碳排放［1］，且仍有增长趋势。作为典型工业化产物的汽车工业，其发展迅速，私家车的数量显著增加，对化石原料的消耗不可忽视。目前，我国汽车油耗占全国油耗总量的25%，对国外石油的依赖度已达到60%［2］，长年累月的汽车燃料消耗将进一步加剧能源短缺问题。另一方面，传统的燃料汽车在消耗不可再生能源的过程中，会不可避免地排放一定量的有害气体，从而加剧环境恶化，不符合我国目前所倡导的碳达峰、碳中和新发展理念［3-4］。

新能源电动汽车EV（Electric Vehicle）有望成为解决上述问题的有效措施之一。相较于传统的燃料汽车，EV 的动力主要来源于电能，其具有低／无污染、高能效等优点，因此EV 的大规模使用对于改善环境、增强对可再生能源的消纳能力、提升电网的供电质量有积极的促进作用。其中，支持车网互动V2G（Vehicle to Grid）技术［5-6］的EV 能够作为柔性负荷，连接到电网中进行充放电，此类新型负荷具有“时空”属性［7］，可以视作移动储能设备。但受个体用户行为的影响，其充电位置和充电时间分散且无序。因此，EV 的充电管理面临着诸多挑战：①随着EV 数量的不断增加，充电需求也增加，且充电负荷会与电网其他负荷的用电高峰重合，导致充电成本过高［8］和供需不平衡问题；②EV 用户的停车和充电行为具有不确定性，EV 无序充电会导致电网电压波动，易引起电网的稳定性问题［9］。

针对上述问题，文献［10］提出了一种实时二进制优化模型，将线性规划方法和两阶段凸松弛方案相结合，实时计算接近最优的EV 充电计划。然而，此类方法依赖模型预测估计EV的充电需求、到达时刻、离开时刻，但是在实际中很难得到精确模型。为了减少模型的不精确性对性能的影响，同时考虑到现实中存在的不确定性，近年来以马尔可夫决策过程MDP（Markov Decision Process）为严格数学基础的强化学习方法被用于解决EV 充电相关的优化调度问题，例如：文献［11］建立了离线的换电站调度模型，并设计了一种带基线的蒙特卡罗策略梯度强化学习算法求解近似最优解；文献［12］建立了基于博弈论的实时电力交互模型，并设计了一种迁移强化学习算法对模型进行求解。

需要指出的是，上述研究工作采用的是基于数据驱动的强化学习方法，所提模型的训练存在维数灾难或迭代次数过多的问题。为了解决随机环境中高维状态空间表征的问题，许多学者通过引入神经网络来提高强化学习模型对数据的拟合能力，例如：文献［13］提出了经验存储的深度强化学习方法，用于克服风电、光伏和负荷的不确定性变化，并以最大化微电网的经济利益和居民满意度为目标，但未考虑EV接入微电网所带来的影响；文献［14］提出了一种基于最大熵值的深度强化学习的充换电负荷实时优化调度策略，考虑了用户因素、系统因素和市场因素，制定了不同的应用场景，但未考虑大量电池老化带来的经济成本问题。目前，关于电动汽车充电站EVCS（Electric Vehicle Charging Station）参与“车-路-网”［15］的能量交互，并考虑其经济性和实用性的研究较少。而大规模的EVCS 作为EV 与电网的“中间商”，是实现EV 与未来能源互联网深度融合的重要组成部分。

基于上述分析，本文从EVCS 的角度出发，考虑分时电价和EV用户行为的不确定性，将深度Q网络DQN（Deep Q-Network）应用于并网EVCS，进行EV充放电行为的在线优化调度，实现EVCS 日运营成本最小化。首先，建立了由充电成本、老化成本、惩罚成本组成的传统成本模型，且考虑到传统MDP 模型无法处理约束的缺点以及用户的行为存在不确定性，构建了一个新的有限回合MDP 模型，并基于传统成本模型提出了MDP 的奖惩回报函数；然后，针对随机环境下模型训练遇到的高维状态空间问题，设计了相应的状态空间和动作空间，并采用一种卷积神经网络结构结合强化学习的方法，通过从原始观测数据中提取高质量经验来趋近最优调度以达到优化目标；最后，基于某典型的公共社区停车场数据进行算例分析，验证本文所提基于MDP 模型的能量管理策略在解决EV 充放电调度问题方面的有效性和优越性。

1 EVCS的系统架构

本文研究的EV充放电调度策略由并网的EVCS决策执行，目的是通过区域内EV与电网进行电能交互，实现EVCS 日运营成本最小化。EVCS 的结构示意图如图1 所示。EVCS 可视为并网的分布式储能装置，其中双向直流充电桩用于V2G 服务，双向交直流转换器在本地电网和EVCS 之间传输电力，以保持直流母线的稳定性。EV 充电装置和电网侧的电力转换器共享1 条直流母线，减少了基础设施投资，提高了能源转换效率。

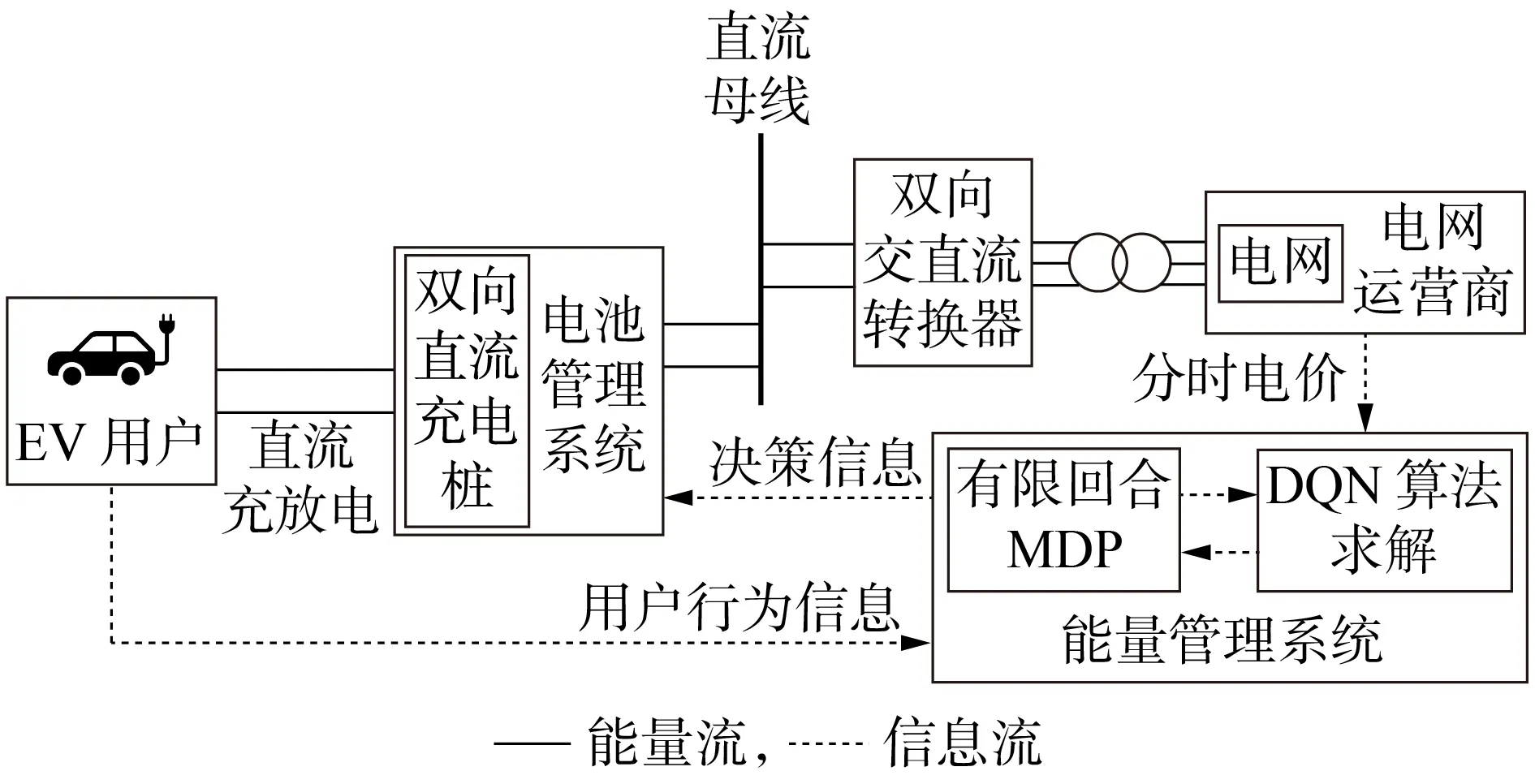
图1 EVCS的结构示意图Fig.1 Structure diagram of EVCS

EVCS 通过协调EV 用户的充电需求、荷电状态SOC（State Of Charge）、电网的分时电价进行优化调度，使系统日运营成本最小化。调度过程涉及电网运营商、EV 用户、EVCS 运营商这3 个角色，其中：电网运营商负责维护电网，并提供基础电力服务，且为了减轻电力需求负担、降低输电维护成本，电网运营商倾向于采用分时电价，以鼓励终端用户参与需求侧能源管理；EVCS运营商在运营过程中被认为是电网的价格接受者，这意味着其不影响电力市场的清算价格，可以通过电价差、提供停车服务获取利润。EVCS运营商考虑分时电价和EV用户行为的不确定性，以日运营成本最小化和延缓电池老化为目标，制定EV的充放电优化调度策略。

2 数学模型

2.1 传统成本模型

EVCS运营商通过优化调度EV的充放电行为以达到日运营成本最小化的目标，目标函数可以表示为：

2.1.2 EVCS惩罚成本

EVCS 惩罚成本主要是指在运行过程中，若EV在离开EVCS 时电池电量没有达到目标电量，则EVCS 需向用户支付的罚款。若EV 离开EVCS 时电池电量大于等于目标电量，则不会产生罚款；若EV离开EVCS 时电池电量小于目标电量，则未满足的电量将以单价ape进行罚款。则惩罚成本可表示为：

2.1.3 EV电池老化成本

长时间充放电调度会导致EV电池逐渐老化，可用容量不断衰减，性能下降。因此，EVCS 需要承担一部分充放电导致的EV电池老化成本，其主要受充放电功率、功率波动等不同因素影响，可表示为：

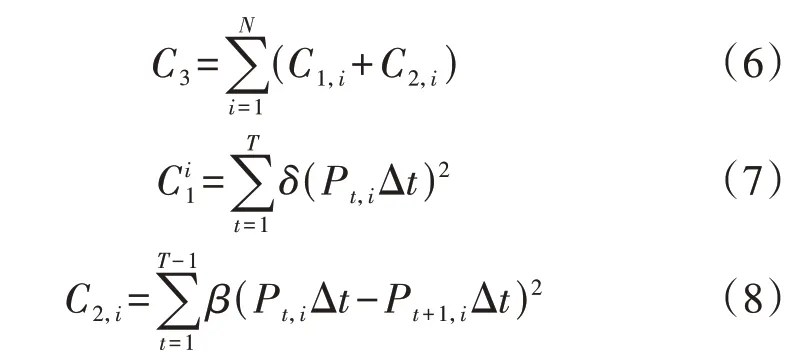
式中：C1，i、C2，i分别为EVi的自然充电损耗成本、充放电状态切换造成的老化成本；Δt为EVCS 进行优化调度的时间步长；Pt，i为t时段EVi的充放电功率；δ为电池自然老化系数，是很小的正数；β为充放电状态切换导致功率变化的老化系数。

电池损耗程度是老化成本的一个关键参数，充电功率会导致电池自然老化，但其损耗较小；充放电状态切换对电池造成的损耗较大，切换状态相邻时段的充放电功率波动越大，则对电池造成的损耗越大。虽然电力电子元器件减少了部分损耗，但充放电过程对电池造成的损耗仍不可忽视。

2.1.4 确定性约束条件

EVCS在EV的可调度时段内将其充电至目标电量，在充电过程中需满足如下确定性约束条件：

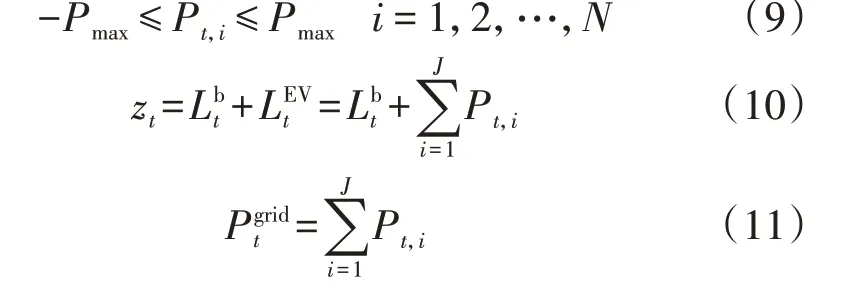
式中：Pmax为EV 的最大充放电功率，受充放电设备和电池容量限制，其值大于0 表示充电，值小于0 表示放电；Pgridt为t时段EVCS 与电网交互的充放电功率；zt为t时段EV 接入后的总负荷；Lbt为t时段电网的基础负荷；LEVt为t时段EVCS 内EV 的综合负荷；J为t时段进行实时充放电的EV数量。

2.1.5 不确定性约束条件

本文主要考虑了EV用户行为的不确定性，包括EV 的到达时刻、离开时刻、初始SOC，通常将这些不确定性因素理想化为服从某种概率分布进行数学建模。本文考虑EV充放电更为实际的情况，所提模型不依赖于概率分布，而是对用户数据集进行随机采样，并主动学习得到每辆EV 的初始信息。则EV 需满足的不确定性约束条件如下：

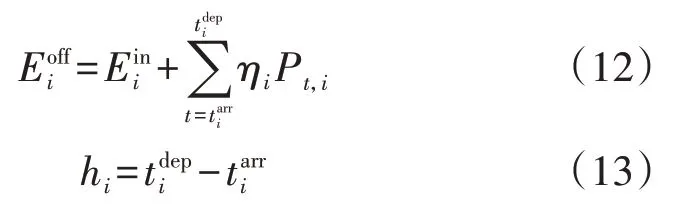
2.2 MDP模型

传统成本模型存在如下问题：①式（7）、（8）、（12）、（13）假定了电池老化系数、到达EVCS 的时刻、离开EVCS 的时刻等参数；②当考虑耦合约束条件式（10）和式（11）时，在转移概率未知的情况下难以在有限的调度周期内获得最优解。传统MDP 需要根据约束假定转移概率矩阵，往往无法应对EV充放电调度任务的广泛性和复杂性。为了解决上述问题，本文设计了有限回合MDP和相应的状态空间S、动作空间A，并基于传统成本模型设计决策过程中的奖惩回报函数R，无需依赖具体的物理模型，可求解得到EV 的实时充放电策略和EVCS 的最优日运营成本。

2.2.1 状态空间

在单个时段t（t=1，2，…，T）内，EVCS 通过观察环境的信息特征积累经验，基于此选择充放电动作以达到优化目标。本文中的EVCS 日运营成本取决于时间步长Δt内电价、充放电动作和EV 到达／离开充电站时刻的变化，因此可以给出MDP 和智能体的序贯模型，如附录A图A1所示。

针对后续求解过程中的状态空间维数问题，设计一个有限的状态空间St，如式（17）所示。

式中：Et，i、Eini、Eoffi为电池状态位，Et，i为t时段EVi的电池电量；xt，i为充放电状态位，表示t时段EVi的充放电状态；Oleave，t，i为停车状态位，表示t时段EVi是否停留在EVCS，若停留则取值为0，若离开则取值为1；fprice为电网的分时电价。

MDP示意图如附录A图A1所示，智能体为接入EVCS 的EV，当EV 数量增多时，系统会出现高维状态空间，可根据智能体的数量进行空间划分，将其解耦［16］为多个单独状态子空间。因此，每个解耦子模型的状态空间维数为24×8阶，分别对应24个决策节点（各调度时段的开始时刻）的EV状态信息。

2.2.2 动作空间

在每个决策节点，智能体EV 有充电、放电和不充不放这3 种可能的动作状态，因此解耦子模型的动作空间为3 元组，在不解耦的情况下t时段的空间大小为3J。显然，解耦模型显著减小了优化问题的规模，提高了搜索速度，增强了实用性。

在解耦子模型i（对应于EVi）中，用xt，i表征智能体的充放电行为，具体取值为：

2.2.3 状态转移

在随机环境中，定义状态转移函数为St+1=f(St，At)，其中f为MDP 随机转移概率函数，其过程较难预测，类似为暗箱模型；下一个状态St+1由当前状态St和当前状态下采取的动作At决定，如式（20）所示。

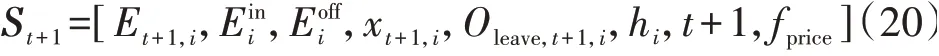
本文所设计有限回合MDP 的状态转移的开始和结束由式（18）决定，充放电状态转移逻辑如附录A 图A2 所示。由于充放电状态的转移很难用准确的概率分布数学模型进行合理的描述，本文采用DQN 算法进行求解，利用训练模型在经验样本中隐式地学习充放电状态转移的概率分布。

2.2.4 奖惩回报函数

EVCS 日运营成本的传统模型以EV 充电成本、EVCS惩罚成本、EV 电池老化成本为优化目标，本节在此基础上，设计了MDP 的奖惩回报函数。模型最终寻优决策使EVCS 日运营成本最小化，所得智能体EV 的策略由MDP 中的奖惩回报函数进行评价，奖惩回报与智能体在当前状态的动作空间（搜索过程）中选择的动作是一一对应的。因此，t时段解耦子模型i的奖惩回报rt，i与当前状态的电量有关，如式（21）所示。下一时段的电池电量Et+1，i与当前状态选择的充放电行为有关，如式（22）所示。

3 DQN算法求解模型

3.1 DQN算法

针对传统MDP 面临的维数灾难问题，即在环境交互过程中产生的状态空间很大且连续，无法用普通的查表法来求解每一个状态-动作价值Q的问题，本文采用DQN 算法，使用深度神经网络来表示状态-动作Q值函数，通过与环境交互学习积累经验以训练求解模型。

MDP 的常规求解方法包括数值迭代和策略迭代，实时动态规划算法［17］是改进的启发式搜索算法，但需要预先设定环境的动力学模型。在本文研究中采用的DQN 算法无需具体的模型处理数据的不确定性。EV 的到达时刻、离开时刻、初始SOC 等信息是难以完美预测的，而本文所提方法不依赖于任何先验信息的假设，随机抽取EV 接入EVCS。MDP 模型能同时获得到达时刻tarri、用户设定的充电目标电量EOFFi、离开时刻tdepi以及初始SOCesoc，i作为状态空间S的初始状态信息，并将到达时刻、离开时刻分别作为有限回合MDP 的开始和结束标志开始训练模型，通过与环境交互生成经验样本(St，At，R，St+1，end)得到最优策略。DQN算法结构如附录A图A3所示。

3.2 DQN算法的实现

DQN 算法无需先验数据进行训练，而是通过智能体和环境交互记录相关的数据(St，At，R，St+1，end)并将其存储为经验样本池，利用深度神经网络来表示Q值函数，且考虑到数据关联会导致网络参数不稳定，通过模型随机更新经验样本池。智能体只需要知道当前状态和动作列表，每个状态-动作组合都有一个与之相关的值，将其称为状态-动作价值Q。Q值函数［18］可表示为：

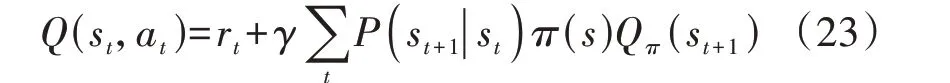
式中：rt为当前状态st执行动作at的奖惩回报；γ∈(0，1)为当前状态预期未来奖励的衰减因子；策略π(s)为状态到动作的映射，表示当前状态st选择的动作at转移到下一个状态st+1；P(st+1|st)为当前状态st到下一状态st+1的状态转移概率；Qπ(st+1)为执行策略π(s)后下一状态st+1的状态-动作价值。

由于MDP 模型中Q值、转移概率矩阵是未知的，在训练过程中DQN引入了2个网络：①固定参数的目标Q值网络，用于固定步长更新参数；②根据评价策略更新参数的动作值函数逼近网络，在每一个时段内进行更新逼近，直至完成神经网络的训练。更新策略如下：

式中：Qt(st，at)、Qt+1(st，at)分别为当前时段、下一时段的状态-动作价值；α∈(0，1)为学习率。式（24）表示状态-动作组合(st，at)的下一个时段Q值为当前时段的Q值加上学习率和下一次估计的误差乘积。新的估计值是当前时段的Q值与下一个状态下可能的最大Q值之和。

在本文设计的有限回合MDP 模型中，如果这个回合有终止标识符，则在这个过程中就不再有未来的状态。因此，式（24）中含γ的项在更新过程中会衰减至0，算法的伪代码见附录A表A1。

4 算例仿真分析

4.1 算例设置

本文以某典型公共社区停车场结合某届“电工杯”的EV 用户真实数据［19］为算例进行仿真分析，部分数据见附录B 表B1。算例的仿真规模主要受J、N这2个参数影响，本文设定J的取值范围为［0，40］辆，N=200辆，即每天接入EVCS的EV总数量为200辆，且各时段EVCS 内的EV 数量不超过40 辆。每天随机抽取EV 用户数据，通过仿真验证本文所提基于MDP 的EVCS 能量管理策略的可行性和有效性。其中EV离开充电站时的目标电量EOFFi由用户设置，EV电池的容量为20 kW·h，充放电功率为3 kW（充电时功率为正值，放电时功率为负值），充放电效率η=0.95。进行调度决策的周期为24 h，时段间隔为1 h，期间功率不变，模型参数设置如附录B 表B2 所示。

在EVCS 的运行过程中，采用我国局部地区的分时电价作为购电电价，具体如附录B 表B3 所示。且考虑到与电网交互功率会产生相关的维护费用，则EVCS 实时地将售电电价asellt设定为购电电价abuyt的95%，如式（25）所示。

采用第3 节所提方法训练MDP 模型，在运行过程中以EV的到达时刻、离开时刻分别作为有限回合MDP 模型的开始和结束标志。模型中S含有8 个变量，即输入的初始状态信息为8 维向量；神经网络结构采用2层全连接层，每层的神经元个数分别为38、16；输出变量维数与动作空间维数一致，为3。模型的学习率α=0.002，衰减因子γ=0.8；设置EVCS 未满足充电需求的惩罚单价ape=1.2 元／（kW·h）。训练过程共进行12000个回合，每个回合随机得到EV 的到达时刻、离开时刻、初始SOC。

4.2 成本结果分析

4.2.1 不同成本函数的优化结果

为了验证所提EVCS 能量管理策略的可行性和有效性，基于真实的用户数据进行MDP 模型训练，并以日运营成本最小化为目标进行优化调度，结果如图2 所示。对模型训练12 000 个回合，行为策略选用ε-贪心探索，将前4 000 个回合作为经验样本池，此时ε=0.8，进行数据初始化后随机选择动作，该过程不学习动作的选择而仅积累经验；训练4000个回合之后，模型开始学习搜索最优的动作，ε在该过程中逐渐减少至0.000 1 并保持不变。ε的衰减过程表示智能体EV 从随机选择逐渐转变为“聪明”地选择最优动作。

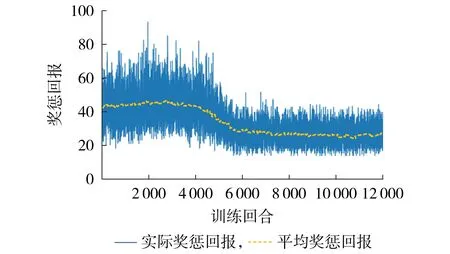
图2 MDP模型的训练结果Fig.2 Training results of MDP model

从图2 中的曲线可看出，局部区域存在波动，这是因为各训练回合开始随机抽取EV，且用户的行为存在不确定性，即EV的离开会使电量和功率状态突然发生改变，该回合的结束环境也需进行初始化，导致各训练回合存在可控的状态差异，使得奖惩回报曲线产生了一定的波动。

设置相同的超参数，MDP 模型考虑EV 电池老化成本对求解过程产生的影响结果见附录B 图B1。由图可看出：模型初期训练的过程大致相同，均在进行随机探索和经验积累，是不断试错的过程；训练4 000 个回合左右时，考虑、不考虑EV 电池老化成本的方案基本寻得一致的收敛方向，由于EVCS 需要求解充放电切换造成的电池容量损耗，考虑老化成本会使模型的收敛速度更慢，且收敛过程波动更大，同时前期的经验存储也更复杂，这增加了模型的训练难度；最终考虑、不考虑EV 电池老化成本的方案都能收敛，且考虑电池损耗确实增加了少量的成本，但延缓了电池老化，这更符合实际情况。

总体而言，在超参数相同的情况下，考虑、不考虑EV电池老化成本的方案都能稳定收敛，虽然考虑老化成本的方案在模型训练前期的难度增大，但随着训练回合的进行，考虑老化成本带来的影响逐渐减小，2 种方案基本在相同的训练时间内稳定收敛，进行实时调度。

4.2.2 不同策略的成本结果

为了评估本文所提基于MDP 模型的能量管理策略（本文策略）的有效性，将其与随机延迟充电RND（Randomly Delayed Charging）［20］策略进行对比分析。2种策略下的日运营成本比较如图3所示（左侧、右侧条形分别对应本文策略、RND 策略）。由图可知：相较于RND 策略，本文策略下EVCS 的日运营成本明显减少，下降了33.6%左右；RND 策略未满足用户需求产生的EVCS 惩罚成本普遍高于本文策略，且第二天的惩罚成本最大；考虑了EV 电池老化成本的本文策略利用分时电价差，减少了部分充电成本，但也产生了少量的电池老化成本。

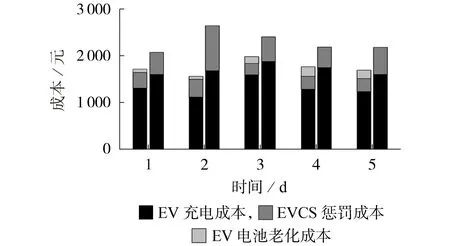
图3 本文策略和RND策略下的日运营成本比较Fig.3 Comparison of daily operation cost between proposed strategy and RND strategy

2 种策略下EVCS 的具体成本（5 d）比较如表1所示。由表可知：相较于RND 策略，EVCS 在本文策略下运营5 d，考虑了EV 电池老化成本的总运营成本为8 661 元，减少了33.6%左右，其中充电成本在电价差的作用下为6 618 元，减少了16.6%左右，EV电池老化成本和EVCS 惩罚成本之和为2 043 元，减少了43.2%左右；EVCS 经过5 d 的运营，本文策略、RND策略下每辆EV的平均日运营成本分别为8.66、11.56元。基于前文的分析，本文策略通过奖惩回报和优化调度充放电行为以适应不同的用户需求，达到了日运营成本最优。

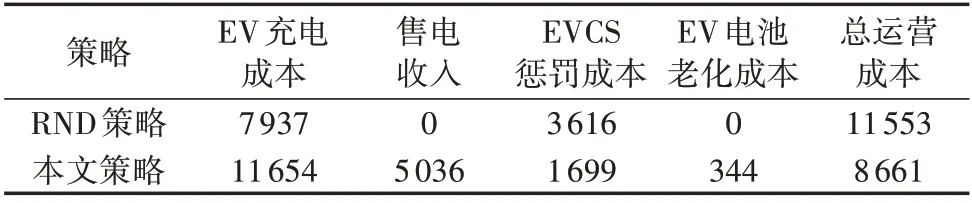
表1 本文策略和RND策略下EVCS的成本比较（5 d）Table 1 Comparison of EVCS cost between proposed strategy and RND strategy（5 days） 单位：元

4.3 充放电行为分析

本文策略以EVCS 日运营成本最小化为目标实时调度EV的充放电行为。为了更直观地说明EV充放电状态的变化，选取20 辆EV 的充放电过程进行分析，并验证考虑电池老化成本的本文策略的有效性。

本文策略下20 辆EV 的SOC 变化曲线如图4 所示。由图可知：当EV 到达EVCS 的时刻处于峰时段（10:00—14:00、17:00—20:00）内时，若EV 的初始SOC较高，则采取放电策略，若EV的初始SOC较低，则在满足充电需求的前提下，采取不充不放策略；当EV 到达EVCS 的时刻处于平时段（07:00—10:00、15:00—17:00）内时，不论EV 的初始SOC 是高还是低，都会采取充电策略。可见，在电网峰平谷分时电价的作用下，EVCS 倾向于在峰时段提供V2G 服务，在其他时段为EV 充电，在降低了充电成本的同时，减少了电网峰时段的用电压力。

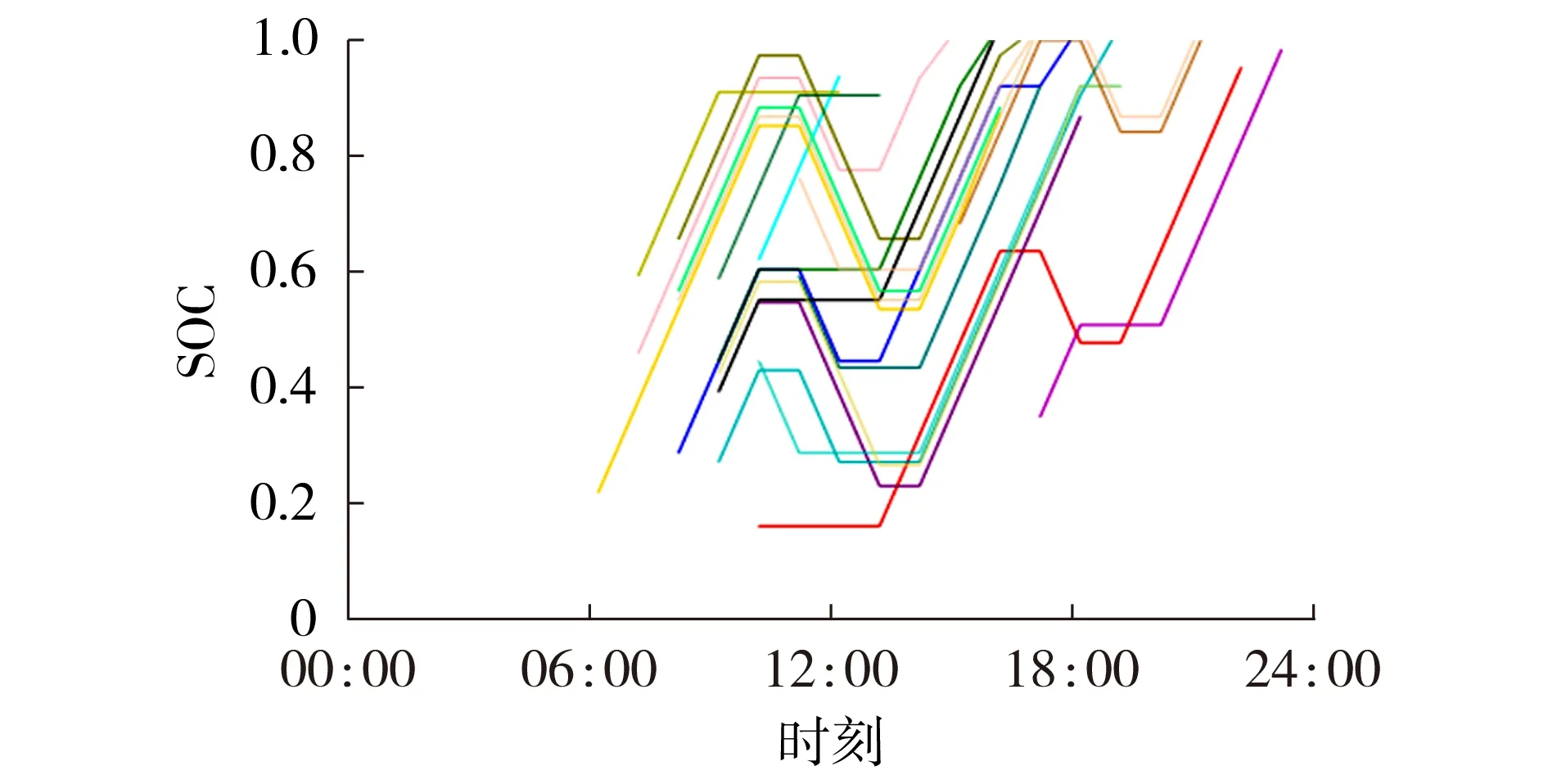
图4 本文策略下20辆EV的SOC变化曲线Fig.4 SOC curves of twenty EVs under proposed strategy

此外，图4 中EV 充电时SOC 呈上升趋势，放电时SOC 呈下降趋势，当EV 的充放电状态发生改变时，SOC 会保持一段时间不变，这是因为本文策略综合考虑电池老化和用户需求，延长了充放电状态的切换时间，减小了充放电功率的波动。

为了验证考虑老化成本的本文策略的有效性，同样选取图4中对应的20辆EV，比较考虑电池老化成本的基于MDP 模型的能量管理策略（本文策略）、不考虑电池老化成本的基于MDP 模型的能量管理策略（MDP 对比策略）、RND 策略下EV 的充放电功率和功率波动，结果如图5所示。

图5 不同的策略下20辆EV的充放电功率比较Fig.5 Comparison of charging and discharging power of twenty EVs among different strategies

由图5 可知：RND 策略下EV 的充放电功率平缓，波动很小，但由表1 可知该策略下的惩罚成本较高；MDP 对比策略能够充分利用峰谷电价差，降低运营成本，但是没有考虑电池损耗，导致在切换充放电状态前、后的功率波动较大（例如在时段10、14、18）；本文策略能够明显减少充放电状态切换前、后的功率波动，而功率波动的减小有利于延长电池的寿命，更符合实际应用需求，且提高了EV 接入电网时的安全性和稳定性。

总体而言，当EVCS 面对相同的EV 用户时：由于用户行为具有不确定性，RND 策略难以满足部分用户的充电需求，虽然充放电功率平缓，不产生电池老化成本，但增加了产生惩罚成本的可能性；本文策略针对充电成本，调度EV在峰时段放电，在平、谷时段充电，针对电池老化问题，延长了充放电状态切换时间，以减小相邻时段的功率波动，且全程考虑了用户的充电需求，使日运营成本比RND 策略降低了33.6%左右。

5 结论

本文利用EV可作为移动储能设备的优点，考虑充电成本、电池老化成本和惩罚成本，降低EV 到达充电站时刻、离开充电站时刻等不确定性因素对优化目标的影响，将有限回合MDP 模型应用于EVCS的能量管理策略。

为了延缓EV 电池老化，本文考虑了EVCS 切换充放电功率造成的电池损耗，适当延长切换时间并采用电力电子元器件进行充放电控制，在一定程度上延缓了电池老化。另外，考虑用户需求设置了相应的惩罚成本，算例结果表明基于MDP 模型的能量管理策略能基本实时满足EV用户的充电需求，具有很强的实用性和扩展性。未来将基于更多的EV 真实数据进行研究，针对不同用户的特征建立多时间尺度调度模型以进一步完善调度策略，在增强鲁棒性的同时，更好地满足用户的需求。

附录见本刊网络版（http：//www.epae.cn）。