考虑响应程度反馈和昼夜充电分布的公交车站双阶段响应模型

2022-10-15姚蓝霓张勇军杨景旭周星月

电力自动化设备 2022年10期

姚蓝霓，张勇军，唐渊，杨景旭，周星月

（华南理工大学电力学院，广东广州 510640）

0 引言

“双碳”目标的提出推动了电力系统加快清洁低碳转型，环保的电动汽车受到了社会的关注和推广［1-2］。公共交通行业因具有可管理性强以及公共服务的特点，成为电动汽车发展的突破口和前沿。然而，大规模电动公交车充电负荷的接入导致电网负荷高峰攀升，峰谷差增大，电网安全经济性降低［3］。因此，如何响应电网需求，有序调控电动公交车充电是亟待解决的问题。

目前，已有较多关于电动汽车参与电网需求响应的研究［4-6］。文献［7-8］研究了电价型需求响应，基于电价激励机制对电动汽车进行有序控制，所提策略在降低负荷峰谷差、用户充电成本等方面具有良好的效果。在关于激励型需求响应的研究中，激励机制的制定是重要一环，但我国的激励机制尚不完善。目前我国各城市主要通过设定补偿单价进行激励［9］，缺乏灵活性，用户的响应质量难以对激励机制形成反馈。因此，部分研究尝试建立考虑用户响应质量的补贴机制：文献［10］建立了一种考虑用户响应特性的需求响应激励策略，以实现多响应场景的兼容性和连续时段的耦合优化；文献［11］对电网的运行风险进行评估，制定了考虑电价调节增益和电网安全性改善效果的补贴机制，但在实际运行中对电网运行风险等级的认定存在一定的困难。且已有关于需求响应的研究大多以私家车为分析对象，实际调控中存在较大的不确定性。而电动公交车由于其用车和充电行为规律，由公交公司进行统一调度，具备良好的可控性［12-13］。

近年来，已有关于电动公交车有序充电调控策略的研究，且从调控时间方面划分，主要可以分为平均划分法和行程划分法。大多数研究采用平均划分法，通常将一天划分为多个时段，然后确定各时段的充电调度计划［14-15］。文献［16］模拟生成了电动公交车的总运行负荷时序曲线，根据运营时段类别和各时段的光伏出力制定充电调度机制；文献［17］建立了充换电站日前优化-实时滚动修正充电优化策略，有效降低了充电费用并平抑了负荷波动。行程划分法是根据电动公交车各趟行程之间的间隙划分调控时段。文献［18］通过控制每个行程结束后的充电时长，避免了时段划分带来的多时间节点求解问题，实现了降维求解。根据电动公交车的充电时段分布特征，可以将其全天的充电时间划为2 个阶段：①夜间充电阶段，电动公交车在该阶段的停车时间长且集中；②日间补电阶段，电动公交车在该阶段利用各趟行程之间的间歇进行补电，充电时间分散且时间较短。所以，考虑到电动公交车的充电时间分布在各阶段存在差异性，本文在夜间充电阶段采用平均划分法，在日间补电阶段采用行程划分法。

针对上述不足，本文基于“夜间充电、日间补电”的模式，提出了一种调控电动公交车有序充电的需求响应方法：对电动公交车在一天内的可调控时段进行编码，控制其充电状态以实现有序充电；建立双阶段充电响应模型，定义行程裕度系数的概念来衡量夜间-日间的充电需求分布，提出基于响应程度的分段激励结算机制，并在此基础上建立以最大化公交车站利益为目标的充电响应模型；提出约束偏离程度函数用于求解带约束条件的优化问题；对比不同策略的仿真结果以验证本文所提策略的有效性。

1 电动公交车的双阶段充电模型

本文将电动公交车在全天的充电过程分为夜间充电以及日间补电2 个阶段：夜间充电阶段是指电动公交车结束一天的行程后，在公交车站内充电直至第二天发车时离开车站结束充电的过程；日间补电是指电动公交车利用日间运营各趟行程之间的间歇进行补电，维持电池具有一定的电量以支撑下一趟行程。在一般情况下，电动公交车在夜间休息的时段跨度较大，能够在夜间充满电，因此在日间补电的频率较低，即一般采取“夜间集中充电，日间偶尔补电”的充电模式。在该充电模式下，电动公交车将充电需求集中在夜间时段，且由于电动公交车的电池容量大，大多采用快充方式进行充电。然而，这样会造成公交车站所在馈线夜间负荷急剧攀升，负荷峰谷差扩大，进而导致馈线容量利用率低、经济性差的问题。因此，需要合理分配电动公交车在夜间和日间的充电需求，建立双阶段充电模型。

1.1 电动公交车的排班模型

电动公交车具有发车规律性强的特点，从公交公司调度中心可以获取某条线路上电动公交车的发车时间表、运营电动公交车数量等信息。日常参与出车任务的电动公交车可以分为2 类：一类为全天运营的电动公交车，从早上发车一直运营到晚上收车；另一类为备用电动公交车，主要在早高峰和晚高峰时段运营，视乘客流量和交通拥堵情况增加车次，以缓解运营压力。为了方便调控，规定备用电动公交车不在本文的响应对象范围内，只对全天运营的电动公交车进行调控。用电动公交车信息集合R储存参与调控电动公交车的基本属性信息和运营信息，如式（1）所示。

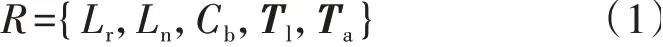
式中：Lr为电动公交车单趟行程的距离；Ln为电动公交车的续航里程；Cb为电动公交车的电池容量；Tl、Ta分别为电动公交车的发车时间矩阵、到站时间矩阵，分别用于储存电动公交车在一天内各趟行程的发车时间、到达终点站的时间。

用Ss，m，r表示电动公交车m在开始第r趟行程前电池的起始荷电状态SOC（State Of Charge），则电动公交车m在结束该趟行程后的SOCSe，m，r可以根据式（2）计算得到。

式中：Tl，m，r+1、Ta，m，r分别为电动公交车m第r+1 趟行程的起始时间以及第r趟行程的结束时间。

1.2 电动公交车的双阶段充电负荷模型

1.2.1 调控时段确定

电动公交车在夜间的停车时间较长，为了方便调控，需要对停车时间进行切割，从而进行分段调控。在对公交车站进行夜间调控之前，收集电动公交车的收车时间Ts以及第二天的发车时间Tf，以T作为单位时段时长，将一天划分为若干个时段。开始调控时段Ns和结束调控时段Nf可由式（4）计算得到。

而日间的停车间歇较短，为了方便调控，可将电动公交车行程之间的间歇作为调控时段。设电动公交车在一天内的间歇总次数为Nb，并将日间调控时段编号为Na+1、Na+2、…、Na+Nb。

夜间和日间的调控时段不同，因此需要储存各调控时段的时长。将各调控时段的时长信息储存在时长矩阵ΔT中，如式（6）所示。

式中：Sa，n为电动公交车在调控时段n的初始SOC；PN为额定充电功率。

2 电动公交车夜间-日间双阶段充电响应模型

为了完成需求响应任务，公交车站通过分配部分充电电量到日间，从而获得更高的激励补贴。因此，本文建立了以公交车站效益最大化为目标的夜间-日间双阶段充电响应模型，以实现电动公交车有序充电日前调度。

2.1 夜间-日间充电电量分布调节机制

电动公交车的充电需求量主要取决于其出车任务量。电动公交车具有规律的出行特征，出车任务量也相对稳定，因此其每天的充电需求量较固定。若将充电电量集中在夜间，则会形成夜间负荷高峰，扩大负荷峰谷差；若夜间充电电量不足，则会加重日间补电的充电任务量，然而电动公交车的间歇补电时间较短，可能难以满足充电需求量而造成出行延误。为了解决上述问题，本文采用“夜间集中充电，日间间歇补电”的充电模式，将电动公交车的部分充电需求量安排在夜间，剩余的充电需求量安排在日间，并定义行程裕度系数来反映充电电量在夜间和日间的分布情况。电动公交车在夜间充电的目标SOC值Sg可表示为：

式中：SL为为了防止电池过放而设置的SOC 下限；g为电动公交车的行程裕度系数，表示电池在维持SOC下限的基础上，能够支撑的行程数。

通过调控g可以决定充电电量在夜间和日间的分配，进而通过控制夜间充电阶段和日间补电阶段电动公交车的充电状态来实现有序控制。

2.2 削峰响应分段激励结算机制

公交车站通过参与电网的削峰需求响应，对站内电动公交车的充电安排进行调控，从而达到目标响应量，并由此获得收入。在实际的响应过程中，响应参与方可能会出现响应量不足或大幅度超额的情况，本文将其分别称为欠响应和过响应［19］。当欠响应时，需要引导用户有效响应，以保证削峰效果；当过响应时，需要在保证任务削峰量的前提下降低电网的削峰成本。因此，本文通过对响应程度进行分段，设置不同的激励结算方式以引导响应参与方在目标响应量的合理偏差范围内进行响应，且用户最终的响应质量将影响其激励补贴。

2.2.1 响应程度划分

为了衡量用户对电网下发的目标响应量的实际响应程度，本文定义了响应时段q的响应系数指标ηq，如式（10）所示。

式中：Pg，q、Pres，q分别响应时段q电网下发的目标响应量、公交车站的实际响应量。

根据用户的响应系数，响应时段q的实际响应结果可分为欠响应、有效响应、过响应3 种情况，具体划分依据如式（11）所示。

2.2.2 考虑响应程度的激励结算机制1）有效响应。

当响应参与方的响应系数达到有效响应规定的范围，即0.8≤ηq≤1.2 时，按照电网当前的基准激励电价进行结算，此时响应参与方的激励补贴Cin为：

3）过响应。

当响应参与方的响应系数过高时，电网会因激励费用支出增加而电网运行经济性改善有限，导致综合经济效益降低，因此需单独对响应参与方的超额响应部分进行结算。过响应的激励电价需在基准激励电价的基础上叠加饱和系数，以减轻电网公司的补偿费用负担。对于1.2＜ηq≤2的超额响应部分，其激励电价Cres，q如式（15）所示；对于ηq＞2的超额响应部分，电网不对其进行补偿。

2.3 公交车站的响应优化目标

公交车站一天的充电费用Cc可表示为：

式中：Qd为公交车站一天的总充电电量。

2.4 约束条件

在电动公交车的充电过程中，需要分阶段考虑约束条件。

2.4.1 夜间充电阶段约束1）目标电量约束。

电动公交车在夜间充电阶段需要充电达到目标SOC，即：

式中：Sn为电动公交车在夜间充电结束后的SOC。

2）行程裕度系数约束。

为了保证电动公交车的出行需求，即电量能够支撑下一趟行程，同时考虑到电动公交车电池的使用寿命，需设定电池的安全使用阈值，因此Sg需要满足以下约束：

式中：Tch，r为第r趟行程与第r+1 趟行程之间的间歇补电时间；Tb，r为电动公交车在第r趟行程与第r+1趟行程之间的间隙时长。

2.4.3 配电网安全约束

为了避免有序充电调控后公交车站的充电负荷与基础负荷叠加产生新的负荷高峰，导致馈线重过载，还需满足以下约束：

式中：Pli，max、P′li，max分别为有序充电调控前、后馈线的负荷峰值。

2.5 公交车站响应控制流程

当局部配电区域出现电力供需缺口或馈线面临过载风险，且电网内部调控能力不足时，可通过发布需求响应任务号召用户积极响应以缓解自身的运行压力。电网公司作为响应主导方需负责判别当前的运行状况，发布并制定需求响应计划，并向参与对象下达响应任务。而公交车站作为响应参与方需根据电网公司下达的任务，进行日前调度，优化站内电动公交车的充电计划，在达成响应任务的基础上，实现自身利益最大化。公交车站的具体响应步骤如下：

1）电网调度中心启动需求响应机制，根据电网的运行情况，确定响应时段和响应任务量，并将其下达给公交车站；

2）公交车站采集相关信息，包括电动公交车的运营时刻表、单趟行程距离、到站SOC、固有属性信息等；

3）公交车站控制中心基于采集所得的信息优化电动公交车在各调控时段的充电状态以及行程裕度系数，完成响应目标并最大化自身利益；

4）公交车站控制中心将有序充电调控后的充电计划下达给对应的电动公交车，电动公交车按照接收的充电计划进行充电，若电动公交车在日间高峰时段因堵车延迟到站，则可适当推迟其充电计划。

2.6 充电响应策略的求解方法

公交车站在收到电网下发的响应任务量后，确定夜间充电阶段的目标充电电量，并对站内电动公交车的充电状态进行控制，从而实现响应目标。因此，将站内电动公交车的行程裕度系数以及各调控时段的充电状态作为优化变量，对电动公交车的充电计划进行优化。

本文的优化模型为一个带多约束条件的优化问题，粒子在迭代过程中往往会出现不满足约束条件的情况。目前，关于约束条件的处理方法包括添加罚函数项以及对不满足约束条件的粒子的适应度赋极值，其中前者的权重设置对优化结果的影响较大，而后者用于处理含较多约束条件的优化问题时，可能陷入局部不可行的范围内，无法实现寻优。因此，本文定义约束偏离程度函数来衡量粒子偏离约束条件的严重程度。基于此，粒子也可能在不可行解中进行寻优，逐步逼近可行解。粒子的约束偏离程度Ddev可表示为：

式中：Sg，m为电动公交车m在夜间充电阶段的目标SOC；Sn，m为电动公交车m在结束夜间充电后的SOC；Td，m，j为电动公交车m在第j个间歇时段补电的延误时长；Nb，m为电动公交车m的间歇时段数量（对于不安排补电的间歇时段，其充电延误时长为0）；γ1、γ2为权重系数。

粒子寻优的规则如下：

1）若2 个粒子均满足约束条件，则对比粒子所在位置的适应度值，适应度值较小的粒子为优；

2）若只有1 个粒子满足约束条件，则满足约束条件的粒子为优；

3）若2 个粒子所在位置均不满足约束条件，则约束偏离程度较小的粒子为优，若2 个粒子的约束偏离程度相等，则对比其适应度值，适应度值较小的粒子为优。

具体的优化求解流程图如图1所示。

图1 优化求解流程图Fig.1 Flowchart of optimization solution

3 算例分析

3.1 仿真参数设置

公交车站通过专变接入10 kV 馈线，馈线的载流量为454 A。基础负荷曲线和充电分时电价如附录A 图A1 所示。公交车站内充电桩的额定功率为60 kW。电动公交车的相关参数参照开沃纯电动公交NJL6100EV6 设定，电池容量为314.14 kW·h，续航里程为300 km。本文所用算例设定共有66 辆电动公交车在站内接受充电调控，且电动公交车环形运行，结束行程后返回车站内。车站安排了2 个发车计划，发车计划1和发车计划2的单趟行程距离分别为20、30 km，具体安排信息分别见附录A 表A1和表A2。其余参数设定如下：权重系数γ1=γ2=1；α和β的取值范围分别为0.2～0.4、0.3～0.5，本文中取值分别为0.3 和0.4。本文以馈线不重载（即馈线负载率不超过80%）为目标确定响应时段和响应削峰量（将全天分为48 个时段），结果如附录A 表A3 所示。为了增加仿真结果的可信度，进行5 次仿真并取其中的最优解。

3.2 本文所提策略的削峰效果分析

公交车站经本文所提优化策略有序充电调控前、后所在馈线的负载率及充电负荷曲线分别如图2、3所示。需要说明的是，电动公交车有序充电从其收车后开始并持续到第二天收车，为了方便展示，本文将负荷曲线绘制在一天范围（00:00—24:00）内。

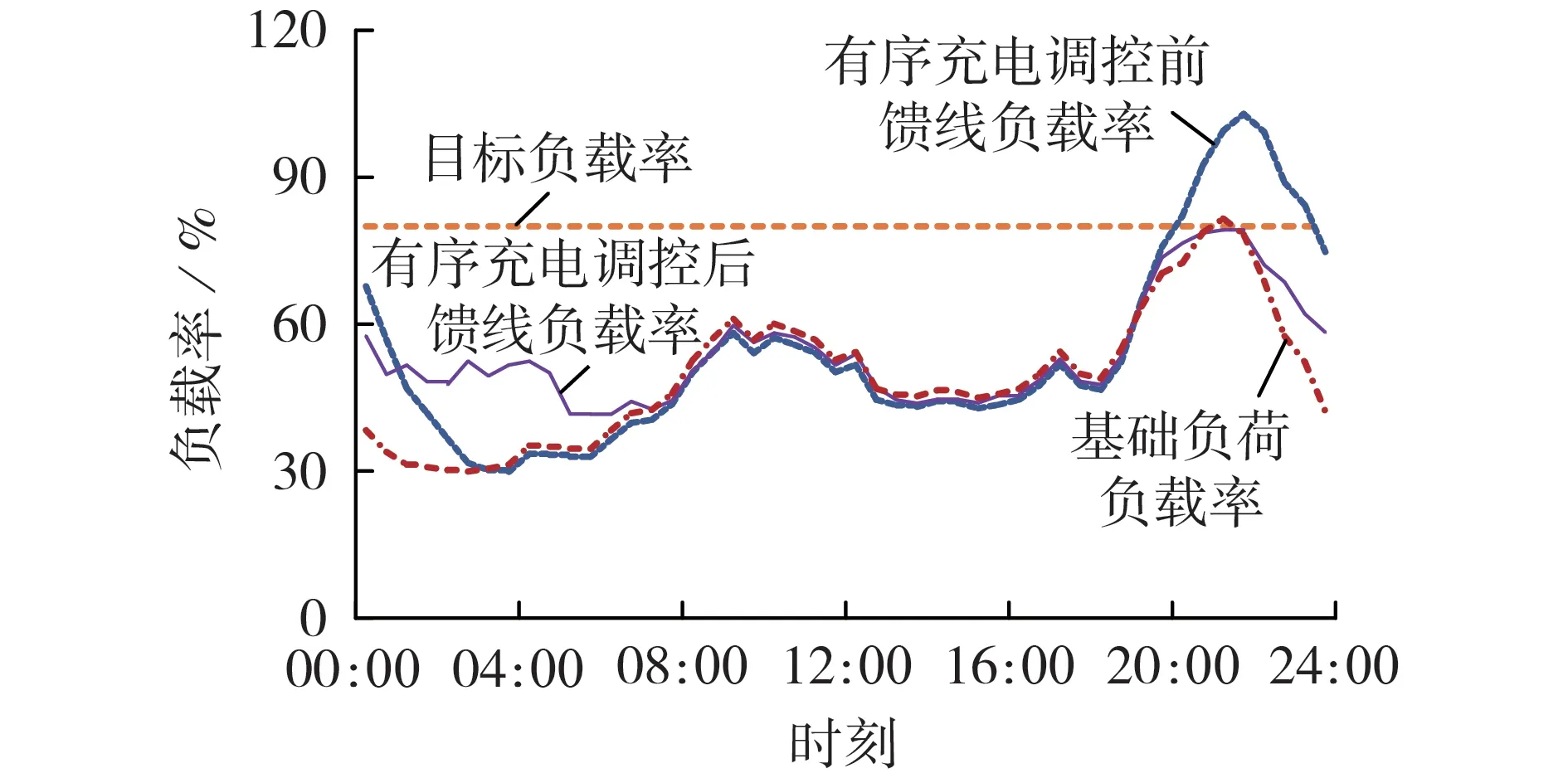
图2 有序充电调控前、后的馈线负载率曲线Fig.2 Feeder load rate curves before and after orderly charging control

由图2 可以看出，馈线基础负荷在21:00 左右达到高峰。由图3 可以看出，有序充电调控前，电动公交车按计划依次在18:00 之后结束一天的行程接入电网进行充电，充电负荷逐渐攀升，在23:30 时刻达到峰值，并在次日的04:00 时刻左右降为0。从基础负荷和充电负荷的时间分布来看，两者的峰值持续时段存在一定程度的重叠，导致“峰上加峰”现象。在20:00—23:00 时段内，馈线负载率超过80%，并在21:30 时刻达到102.9%，严重威胁电网的经济安全运行。经过本文所提策略有序充电调控后，馈线负载率下降到80%以下，显著降低了重过载风险，20:00—21:30 时段内的充电负荷得到大幅削减，大部分充电需求被转移至次日01:00之后，小部分充电需求被转移至日间。

图3 有序充电调控前、后的充电负荷曲线Fig.3 Charging load curves before and after orderly charging control

以站内某一辆电动公交车为例，其在夜间充电阶段各调控时段的充电功率如图4 所示。由图可知：有序充电调控前，该电动公交车的夜间充电时段主要为时段39—44（即18:00—22:00），其中时段43—45 的馈线负载率甚至超过100%；有序充电调控后，时段43—45 的充电功率都为0，说明本文所提优化策略可以有效避免电动公交车在馈线运行状态恶劣的时段充电，而是将其转移到负载率较低的时段进行充电。

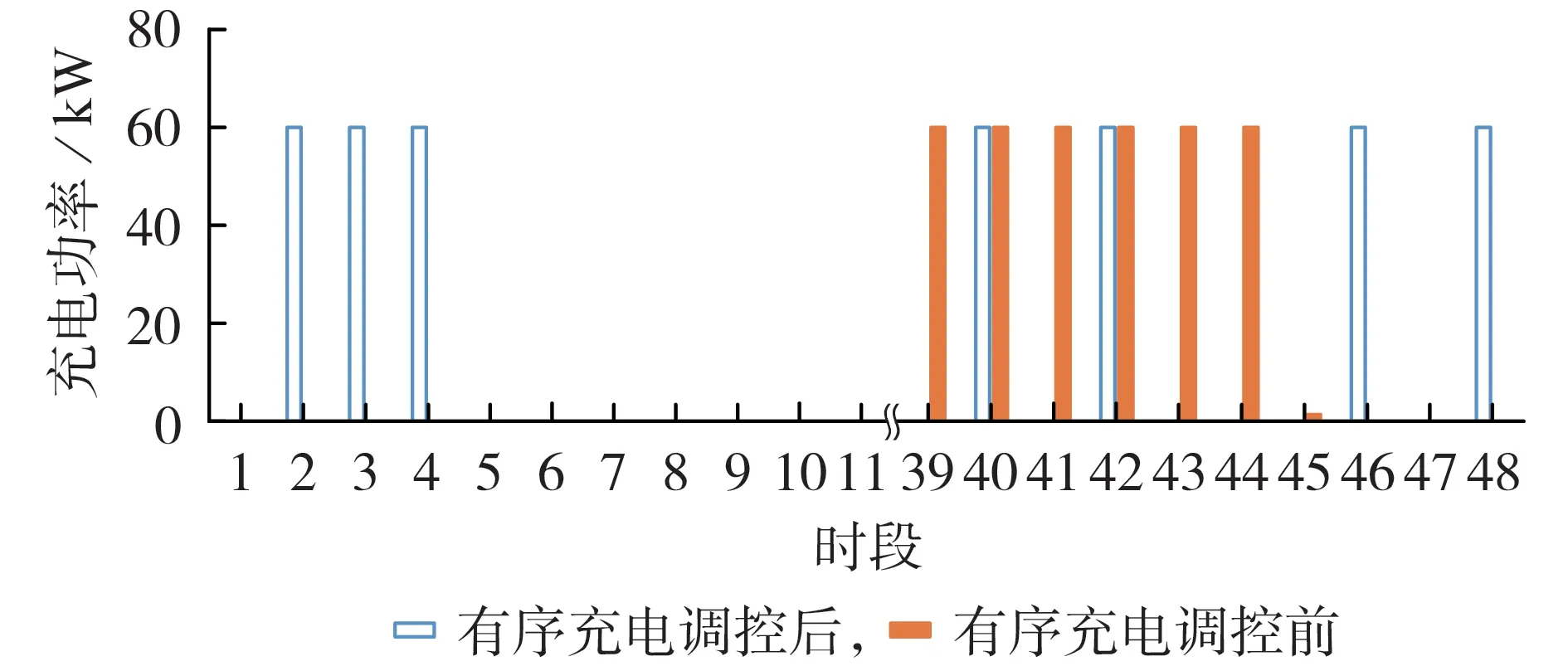
图4 有序充电调控前、后某辆电动公交车的充电功率Fig.4 Charging power of an electric bus before and after orderly charging control

3.3 本文所提策略的有效性分析

为了验证本文所提策略的有效性，设置以下3种策略进行对比分析：①策略1 只在夜间进行有序充电，并采用本文所提分段激励结算机制；②策略2采取本文所述“夜间充电、日间补电”的模式，但采用固定激励方式，对于响应量为响应目标量2 倍范围内的部分按固定的激励价格结算，对于响应量超出响应目标量2倍范围的部分不予结算；③策略3为本文所提优化策略，即考虑“夜间充电、日间补电”的模式，并采用分段激励结算机制激励用户。

上述3 种策略在响应时段内的响应结果见附录A 表A4，其余仿真结果见附录A 表A5。3 种策略优化后的充电负荷曲线如图5所示。

图5 3种策略优化前、后的充电负荷曲线Fig.5 Charging load curves before and after optimization of three strategies

1）夜间-日间充电分布调节机制有效性分析。

对比策略1 和策略3 的优化结果：由表A4 可知策略3 在各响应时段都能实现电网下发的响应目标，而策略1 在响应时段42—44（即20:30—22:00）内的响应系数小于1，馈线仍处于重载状态，尤其是在时段43，馈线负载率达到85%，重载程度较严重；由表A5 可知，在激励补贴方面，由于策略1 在部分时段未能实现响应目标量，甚至出现欠响应的情况，导致电动公交车的激励补贴少于策略3；由图5可以看出，策略3 利用电动公交车在日间的休息时间间歇补电，将部分充电需求转移至日间，其充电电量的时间分布相较策略1更广泛，且削峰率比策略1提高5.55%，负荷峰谷差比策略1 减少405.9 kW。可见，只在夜间有序充电难以实现较大程度的负荷转移，削峰能力有限，策略3 的削峰效果比策略1 好，能够完成更高要求的响应任务。

关于公交车站的经济效益，若电动公交车不参与需求响应，其单位电量净支出为0.95元／（kW·h），而经策略1 和策略3 优化后的单位电量净支出分别为0.39、0.31 元／（kW·h），相较电动公交车不参与需求响应时的结果分别降低了58.9%和67.4%。可以看出，虽然日间的电价较夜间凌晨时段的电价高，但转移小部分的充电电量至日间并不会减少公交车站的效益，反而会因为响应效果好而获得更多的激励补贴，使公交车站更有动力参与需求响应。综上所述，相较于策略1，策略3的削峰潜力更大，响应质量更好，可以获得更多的激励补贴，提高公交车站的经济效益。

2）激励机制有效性分析。

由表A4中各时段的响应系数可知，相较于策略3，策略2的响应系数分布波动更大，有3个时段的响应系数低于1，且有3个时段的响应系数高于3，即使策略2 下部分时段的降载效果显著，但时段43（即21:00—21:30）因公交车站欠响应，此时的馈线仍处于重载状态。另外，策略2 的削峰率和负荷峰谷差指标均不如策略3。

由表A5 可以看出，相较于策略3，策略2 下公交车站获得的激励补贴增加了1 829.8 元，提高了约20%。从激励补贴制定方即电网公司的角度出发，这种低效高支出的削峰激励补贴机制显然是其不能接受的。而本文所提分段激励结算机制可以引导公交车站实现有效响应，有效避免部分时段大幅度过响应而部分时段欠响应的情况发生。所以，相较于固定激励方式，基于响应程度的激励结算机制给电网带来的经济负担更小，且能有效引导用户实现更高质量的响应。

此外，本文还对算法的收敛情况进行了分析，具体结果见附录B。