考虑电动汽车用户意愿的滚动优化调度

2022-10-15王誉博龚庆武张劲弦

电力自动化设备 2022年10期

王誉博，龚庆武，乔卉，刘栋，张劲弦

（武汉大学电气与自动化学院，湖北武汉 430072）

0 引言

电动汽车（EV）的普及是实现碳中和的有效手段之一。随着电池价格的不断降低，电池的大规模应用已成必然趋势，会引起一场能源革命。EV 用户的充放电需求各不相同，如果不进行合理的规划，则会导致无序充放电行为，其大规模接入电网时会对电网用户侧造成较大的冲击与影响［1］。

目前，已有较多关于EV 调度策略的研究：文献［2］综合考虑风力发电与EV 两者的随机性，将系统的等效负荷方差作为优化目标来抑制负荷的波动并增加对夜间溢出风电的消耗，但并未考虑EV实际参与调度的意愿，且优化目标较单一；文献［3］采用蒙特卡罗仿真方法，在考虑不同EV渗透率下充电行为对配电网造成影响的基础上，给出了EV充放电功率曲线，并基于算例验证了EV 在双向车网互动V2G（Vehicle-to-Grid）模式下的充放电行为能够对系统起到削峰填谷的作用，但并未给出导致EV渗透率差异的影响因素，未能体现EV 参与调度的意愿；文献［4］建立了一个随机的经济调控模型，在充分考虑EV 与风电出力随机性的情况下，以最小化系统总发电成本期望值为目标函数，并验证了所提模型能够减少发电成本，有效提高调度方案的经济性。上述研究主要从电网侧角度出发，对于EV用户的利益考虑较少。为了吸引EV 用户主动参与调度，需要对EV 用户的经济性多加考虑。文献［5］考虑到未来EV 数量庞大，论述了调度机构对EV 进行直接控制的策略会增大优化问题的求解难度，为此提出了对EV 充放电行为进行分层管理优化调度的理念。虽然分层管理可以有效优化EV 调度问题，但是EV 是否愿意被调度仍无法确定。若不考虑EV 用户的需求，则会大幅影响实际可调度EV 的数量。文献［6］以配电网区域的网损最小为目标函数，并综合考虑了电力系统经济运行等方面，通过算例仿真验证了所提方法不仅能够有效地降低配电网网损，还能够对负荷起到削峰填谷的作用，并有效改善系统的电压质量。但是在EV不断渗透的情况下，不能将优化目标仅局限于电网自身的运行状态，需要多关注EV这种特殊负荷的参与深度。文献［7］在综合考虑已有EV优化充放电调度策略的基础上，提出了配电网层面的未来EV 充电调度策略需要考虑用户充电行为的随机性。虽然文献［7］中策略已初步考虑了EV参与调度的随机性，但是对于如何刺激用户主动参与调度还缺乏分析。文献［8］建立了一种多目标EV充电优化调度策略模型，以充电费用和蓄电池循环电量为多目标进行优化，并与“停车即开始充电”方案进行了仿真对比分析，验证了所提调度策略的优越性。文献［8］涉及了EV 用户的经济需求，但是没有考虑EV 用户的出行需求、参与意愿以及用车时间，且对于大量EV接入后如何保证电力系统稳定运行的问题仍缺乏深入研究。文献［9］采用层区分离的方法对EV进行充放电调度，选取负荷波动最小作为上层模型的目标函数，对电力系统及各EV代理商进行协调优化，合理分配各代理商在各时段的充放电负荷；在下层模型中，通过调控可调度EV 群体各时段电池的充放电状态，使各EV代理商能够完成调度任务。若在下层模型中进一步考虑EV 用户的需求，则可以最大限度地吸引EV 用户参与调度，即可以增大可调度EV的数量。

综上所述，已有研究对于EV用户参与调度的意愿考虑较少，为此本文研究主要通过考虑EV用户参与调度的意愿来吸引更多的EV用户主动参与调度。首先，建立EV模型，并提出行为倾向函数，其中包含了EV的当前状态、剩余电量、未来出行距离、上一时段的充放电状态、停车时长等信息，以此实现为EV用户提供精准服务；然后，根据EV 用户的行为倾向对EV 进行聚合分类，并针对每种类型EV 设计独立的调度策略；最后，考虑EV 双向互动参与下的配电网网损、风电与EV 充电功率的匹配效果、充电时段内负荷方差的大小构建多目标优化调度策略，并在此基础上综合考虑每一辆EV 的荷电状态SOC（State Of Charge）、EV用户的实际需求、配电网的功率与电压等约束条件，在全天时间尺度下对每种类型EV的充放电策略进行动态优化。

1 EV模型及行为倾向函数

EV 在电网中作为一种特殊的负荷，既具有电源性质，又具有负荷性质，其灵活性可以为电网的运行带来诸多益处。EV 用户与调度中心的数据交互通过手机APP实现，由调度中心建立某种软件为EV用户提供服务，EV 用户可以在该软件上提交车辆是否处于行驶状态、是否愿意参与调度、剩余电量以及预计出行距离等信息。

1.1 EV调度及充放电模型建立

本文采用马尔可夫决策过程MDP（Markov Decision Process）构建EV充放电调度模型［10］。MDP可用一个四元组M=(S，A，psa，R)表示，其中S为一组有限的状态集，A为一组有限的行为集，psa为状态转移概率，R为回报函数。

t时段风电与EV 组成的系统状态空间St可表示为：

恒流-恒压充放电模式是一种常用的电池充放电方式，该模式可以使调度控制的实施更加方便，所以本文中的所有EV 均采用恒流-恒压模式进行充放电。

t时段第k辆EV 的充电电量ec，t、放电电量ed，t可分别表示为：

由于本文利用EV 的初始停车时间和停车时长lk描述其停车事件，且与初始停车时间和所需充电电量相关，故假设模型中所有EV停车事件的停车时长lk均服从截断高斯分布［11］。

假设EV 行驶距离服从自由度υ为3.487 5 的卡方分布，且耗电量与行驶距离成正比。因此，可以根据式（8）计算EV下一次出行时所需的最小电量ek。

式中：dk为第k辆EV 的行驶距离；ω为EV 每行驶1 km的耗电量。

第k辆EV的初始剩余电量ecap，k服从均值为0.6、标准差为0.1的正态分布［12］，即可表示为：

式中：X为正态分布的随机变量。

1.2 考虑EV用户行为倾向的EV聚合分类

本文提出了一种评估函数用于评估EV 用户的主观行为倾向，以此衡量EV停车接入充电桩后充放电行为的倾向，以便统计得到各时段参与电网调度的EV 数量。通过计算实现EV 分类，使得EV 的充放电行为达到用户侧经济性最优，有效地减少EV电池状态频繁切换带来的电池损耗，同时满足用户下一次出行电量需求。

1.2.1 行为倾向评估函数构建

本文构建函数FInc用于评估EV 的充放电行为倾向，如式（10）所示。

式中：α、β、γ为权重系数，满足α+β+γ=1；Ecap为EV车载电池的容量；prav为每天的平均电价；pt为当前t时段的分时电价；Scha为EV 停车后充放电状态切换次数。

1.2.2 EV聚合分类

由式（10）可知行为倾向评估函数FInc的取值范围为[-1，1]∪{2}。为了便于调度方案的规划，遵循同类别内个体EV的状态不能相差过大的原则，本文根据一定的划分方式，将FInc取值在(-1，1)范围内的EV 划分为10 种类型，这一部分EV 的充放电状态是未定的，且FInc取值越接近-1，该EV 在当前时段内放电的倾向越高；FInc取值越接近1，该EV 在当前时段内充电的倾向越高；当FInc取值为0时，表示EV 用户既不想充电也不想放电。因此，这10 种类型EV接入电网后可以参与调度。而根据行为倾向评估函数自身含义的制约，当FInc取值为-1、1、2 时，EV 的充放电状态是确定的，即：当FInc=1 时，EV 处于充电状态；当FInc=-1 时，EV 处于放电状态；当FInc=2 时，EV处于不接入电网的状态。

由上述分析可知，除了充放电状态已经确定的3 种类型EV 之外，各时段真正参与电网优化调度的EV 为FInc取值在(-1，1)范围内的10 种类型EV。本文采用均分EV 数量的方法，即将所有EV 的FInc取值按照从小到大的顺序排序后统计EV数量，然后按照每种类型EV数量相等的原则进行分类，当分类结果出现非整数时，前9 种类型EV 数量的确定采用四舍五入的原则，剩余EV 则划分为第10 种类型。例如：若FInc取值在(-1，1)范围内的EV 共有503 辆，则前9 种类型EV 数量分别为50 辆，第10 种类型EV 数量为53 辆；若FInc取值在(-1，1)范围内的EV 共有497 辆，则前9 种类型EV 数量分别为50 辆，第10 种类型EV 数量为47 辆。根据上述方法进行EV 聚合分类的优点在于可以保证每种类型EV 的可调度总电量差异较小。

1.3 模型的约束条件

1）EV充放电功率约束。

t时段第k辆EV所需电量应满足：

3）潮流等式约束。

2 EV滚动优化调度策略

在线调度是与静态离线调度相对的一种动态调度策略，为了计及风电和EV 的不确定性，本文采用基于蒙特卡罗模拟［15-16］的滚动调度策略在线更新优化调度方案。蒙特卡罗模拟方法的基本求解思路为：建立一个概率模型或随机过程，通过随机抽样获得近似解。本文中每辆EV 的停车事件可以通过调度机构的大数据预测模型得到其概率分布，而EV的充电、放电模式选择行为是一个0-1 离散变量，且在EV 充放电模式选定的情况下，对EV 进行充放电的动作指令也是一个0-1离散变量。

由于风电功率波动大，对其预测较困难，且精确到分秒的EV实时调度太过繁琐，为了减小调度方案的误差，及时有效地调度可用EV，本文选择以1 h为时段间隔（即将1 d 分为24 个时段进行调度），统计EV 信息和风电机组的实时发电情况，每经过1 h 对数据进行1次采样，系统的状态也相应变化一次。

2.1 滚动调度策略的优化目标

1）配电网网损最小化。

本文所考虑的风力发电站采用并网运行的方式，因此需要将配电网的输电成本考虑在目标函数之内，采用配电网区域内的有功网损进行衡量，如式（17）所示。

2）风电与负荷的匹配偏差度最小化。

为了最大化风能利用率以减少弃风现象的发生，在本文所提EV 充放电调度策略中，需要考虑EV作为负荷时其充电功率以及常规用电负荷与风力发电站所发功率之间的匹配问题。为了衡量匹配效果是否合理，本文定义了式（18）所示匹配偏差度Mt。风电与负荷之间的匹配度越高，则匹配偏差度越小，表明EV 作为负荷较好地吸收了风力发电站提供的多余电能。

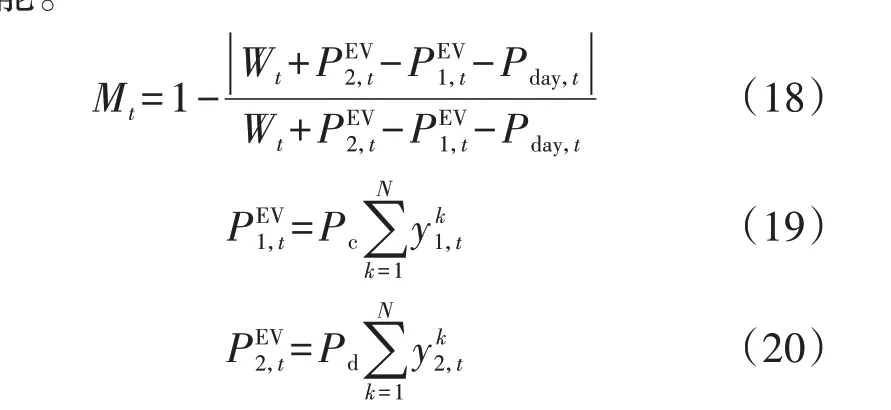
3）负荷方差最小化。

为了防止EV 聚集在某一时段充电造成新的负荷高峰，从而危害电网的运行安全，本文引入负荷方差作为优化目标函数之一，用以平滑负荷曲线。由于本文是基于多时间尺度下的分时段调度，可以通过预测未来接入电网的EV 数量并结合其他用户的用电情况来实现负荷预测。总负荷方差FΔ可以表示为：

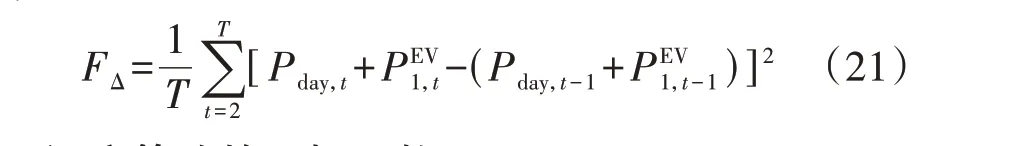
2.2 调度策略的目标函数

基于上述优化目标，综合考虑系统需求，建立t时段调度策略的优化目标函数Ct(St，Aa，t)为：

综合上述内容可以看出，基于EV 在当前时段的行为状态，根据式（23）能确定该时段内EV的充放电调度策略。

3 算例仿真

为了验证本文所提方法的有效性，以IEEE 33节点系统为算例进行测试。根据不同的情况获得配电网网损、匹配偏差度、负荷方差、充电费用等数据，并进行比较分析。

3.1 测试环境及相关参数

IEEE 33 节点系统是一个三相平衡径向配电系统，本文选取节点1、9、18 分别作为风力发电站、EV充电站、火电厂的接入节点，其余节点作为普通用户群节点。本文中的EV 为比亚迪E6 型EV，其车载电池的相关参数［17］如下：电池容量为60 kW·h，充电、放电功率均为3 kW，单位耗电量为0.195 kW·h／km，循环使用次数一般大约为4 000 次。优化仿真的EV总数量为500 辆。EV 充电的峰谷分时电价参考文献［18］。

3.2 不同权重系数下的优化调度结果对比

由于本文的滚动优化调度方法涉及多个目标函数，不同的权重系数取值会产生不同的仿真结果：当λ1=1、λ2=λ3=0，即仅考虑配电网网损时，所得优化调度结果如附录A 表A1 和图A1 所示；当λ2=1、λ1=λ3=0，即仅考虑匹配偏差度时，所得优化调度结果如附录A 表A1 和图A2 所示；当λ3=1、λ1=λ2=0，即仅考虑负荷方差时，所得优化调度结果如附录A 表A1和图A3所示。

当λ1=1、λ2=λ3=0 时，以配电网网损最小为目标进行优化。由附录A 表A1 和图A1 可知，此时的配电网网损最小，但负荷方差明显较大。这是因为：为了保持配电网网损最小，EV 参与放电的总电量较小，EV 群体表现出的负荷性质较多，而表现出的储能性质较少，导致系统的负荷方差较大。同时可以看出，此时的平均放电费用小于平均充电费用，导致EV 用户在参与电网调度过程中所获收益减少，这是因为EV参与放电时段的电价不高，而充电时段的电价较高，且充电时长远大于放电时长，所以总充电费用远大于总放电费用，这会对EV用户主动参与调度的积极性产生影响。

当λ2=1、λ1=λ3=0 时，以匹配偏差度最小为目标进行优化。由附录A 表A1 和图A2 可以看出：此时风电与负荷之间的匹配度最高，说明EV的参与使得风电功率与负荷功率之间的匹配性最好；此时的配电网网损有所增大，但负荷方差相比λ1=1、λ2=λ3=0 的情况有了明显的改善，这是因为系统为了保证风电功率与负荷功率有更好的匹配性，使得EV参与调度的容量明显增加，EV 群体不仅表现出负荷性质，还表现出优质的储能性质，促使负荷发生转移。此时的平均放电费用大于平均充电费用，表明EV作为负荷的充电时段被转移至电价较低的时段。为了满足EV 用户的出行需求，必须保证EV 的剩余电量充足，所以充电容量大于放电容量，导致总充电费用大于总放电费用。但是这种情况大幅降低了EV 用户的总费用，这会促使EV 用户积极主动地参与调度。

当λ3=1、λ1=λ2=0 时，以负荷方差最小为目标进行优化。由附录A 表A1 和图A3 可知，此时的负荷方差值最小，风电与负荷之间的匹配度较高，与λ2=1、λ1=λ3=0 情况的优化结果相差无几。这说明EV 参与负荷调整的同时也可以使风电功率与负荷功率具有很好的匹配性。从平均充电费用较低而平均放电费用较高可以看出，EV 的充电时段均安排在电价较低的时段，而放电时段被安排在电价较高的时段。而电价较低的时段恰是普通负荷用电较少的时段，此时EV 表现出负荷性质；电价较高的时段是普通负荷用电较多的时段，此时EV 体现出储能性质。这种错峰充放电的安排使得峰值负荷得到了有效转移，因此此时的负荷方差最小。但是由于EV的放电电量有限，这导致总放电费用较总充电费用低，致使EV用户在参与调度时获得的收益有限。

多目标优化下权重系数的取值情况较多，以下给出了3 种常见情况：当λ1=0.6、λ2=0.1、λ3=0.3 时，优化调度结果如附录A 表A2 和图A4 所示；当λ1=0.2、λ2=0.7、λ3=0.1时，优化调度结果如附录A 表A2和图A5 所示；当λ1=0.3、λ2=0.2、λ3=0.5 时，优化调度结果如附录A 表A2 和图A6 所示。从上述结果中可以看出：相较于单目标优化，多目标优化下的结果中没有极端数据出现；对于EV 用户而言，多目标优化下的收益较高，这对EV用户主动参与调度有更大的吸引力。但是上述情况并不是多目标优化的最优情况。

通过多次对比测试发现，当λ1=0.2、λ2=0.4、λ3=0.4 时，所得优化调度结果最优，将此时的权重系数称为最优权重系数。最优权重系数下的优化调度结果如表1和图1所示。图中：总充电功率和总放电功率分别为10 种类型EV 的充电功率（为正值）和放电功率（为负值）之和；总充放电功率为总充电功率与总放电功率之和。由于需要尊重EV用户的意愿，所以每一种类型EV都有独立的充放电策略，这会导致某些时段某几种类型EV 正在充电，而某几种类型EV正在放电的情况。

图1 最优权重系数下的优化调度结果Fig.1 Optimal scheduling results under optimum weight coefficients

表1 最优权重系数下的优化调度结果Table 1 Optimal scheduling results under optimum weight coefficients

由表1和图1可以看出，最优权重系数下的总匹配偏差度、配电网网损和总负荷方差结果均不是最优的，但最优权重系数下的总匹配偏差度与仅考虑匹配偏差度的单目标优化结果相差很小，最优权重系数下的配电网网损仅比仅考虑配电网网损的单目标优化结果稍高，最优权重系数下的负荷方差比仅考虑负荷方差的单目标优化结果高25%左右。与其他多目标优化情况相比，最优权重系数情况所得结果都较好，而且此时的总充电费用与总放电费用的差值最小，这意味着EV用户在参与调度时可以最大限度地获得利益。该情况可以非常高效地吸引EV用户主动参与调度。

3.3 传统调度策略与本文调度策略对比

为了证明本文所提多次预测滚动优化调度策略在全天时间尺度下优化结果相较于传统调度策略的优越性，采用控制单变量方法以便进行直观的比对，分别以配电网网损、总匹配偏差度、总负荷方差最优为目标，得到某7天的调度结果如表2所示。

表2 2种调度策略的单目标优化调度结果对比Table 2 Comparison of single objective optimal scheduling results between two scheduling strategies

在传统调度策略下，每个调度时段的寻优往往只保证当前时段的结果最优，这样会使得全天的调度结果不一定是最优的；而本文所提多次预测滚动优化调度策略因加入了日前预测以及实时的未来预测，从而可以从全局的角度出发确保全天调度结果最优。由表2 可见，从全天的角度来看，本文调度策略的优化调度结果明显优于传统调度策略。

多目标优化调度策略与单目标优化调度策略有所不同，因为多目标优化调度策略需要兼顾3 个影响因素，所以其优化结果的优势并不一定非常明显。2 种调度策略的多目标优化调度结果对比如表3 所示。由表可知，相较于传统调度策略，本文调度策略下每个优化目标的结果都有一定的优势，虽然提升的空间不够大，但是从全天时间尺度的结果而言仍具有一定的优势。这说明本文调度策略能够在保证配电网网损处于较低水平的同时，平滑负荷曲线并提升EV就地消纳风电的能力，从而验证了所提策略是切实、有效的。