基于智能合约的电动汽车充电服务费自适应调整机制

郭伟嘉，刘敦楠，王 文，韩金山，刘明光，苏 舒，张 悦，邹孟娇，杨 烨

（1. 华北电力大学 经济与管理学院，北京 102206；2. 国网电动汽车服务有限公司，北京 100032）

0 引言

碳达峰和碳中和目标的提出，对我国新型电力系统的低碳绿色发展提出了更高的要求。其中，大规模电动汽车接入作为新型电力系统的一大重要特征，为“双碳”目标的达成做出了重要的贡献，但同时也为配电网的运行带来了较大的负担［1-2］。因此，如何对电动汽车进行激励引导，促进新型电力系统的智能化发展，具备重要的现实意义。现阶段我国针对电动汽车的激励引导主要来自价格激励，其资金来源于电力市场交易收益或价差，资金规模相对较小，无法满足大规模电动汽车行为引导的需要。相较而言，电动汽车充电服务费单价较高，在电动汽车用户充电成本中的占比较大，是开展电动汽车激励引导的潜在资金来源，但尚未被合理有效引导。同时，由于电动汽车负荷具备很强的实时性、随机性，传统的集中式充电合约很难满足现阶段新型电力系统的定价需要。因此，如何运用新技术，实现更加精确、灵活的电动汽车充电服务费定价，以满足新型电力系统下电网的调控需求，提高用户及充电站的收益，具备重要的研究意义。

在充电服务费定价方面，我国的充电服务费发展可分为以下3 个阶段：阶段1（2015—2020 年）采取统一或分地区的充电服务费，定价的灵活性较低；阶段2（2020—2022 年），国家发改委于2020 年发布了《关于电动汽车用电价格政策有关问题的通知》，进一步放开了电动汽车充电服务费的定价限制，实行市场调节价，极大地提高了电动汽车充电服务费的定价浮动空间；阶段3（2022 年以后），将根据负荷预测情况及电网调控需求实现针对单座充电站乃至单辆电动汽车的充电服务费灵活调整。在充电服务费定价灵活性需求不断提高的趋势下，如何建立更具针对性、实时性的电动汽车充电服务费定价机制，在保证用户及充电站收益的同时满足电网的调控需求，具有重要的现实意义。

针对充电服务费定价问题，国内外学者已经进行了大量的研究：文献［3］提出了一种考虑社会发展、电动汽车保有量、充电站建设成本等因素的充电服务费定价方法；文献［4-7］考虑电动汽车的接入随机性特征及其对电网的影响程度，分别提出了电动汽车有序充电的聚合调度以及定价优化策略；文献［8］考虑充电运营商之间的竞争，提出了一种充电服务费的定价博弈模型；文献［9］分析了电动汽车接入对配电网的影响，进而分析了分时定价对电动汽车接入的影响程度；文献［10］分析了分时电价对电动汽车充电负荷的引导作用，考虑需求响应及电动汽车车主的充电利益，提出了分时电价优化策略；文献［11-12］对当前电动汽车充电模式下的充电设施成本及经济效益进行了研究，并以此为基础进行充电服务费定价；文献［13］考虑综合用户的偏好及收益水平，建立了基于前景理论的浮动服务费多目标优化模型；文献［14-17］研究了基于分时电价的电动汽车有序充电引导策略，旨在在降低电动汽车聚合商的购电成本以及用户充电费用的同时，实现新型电力系统下电动汽车充电负荷的友好接入。上述一系列研究克服了传统统一定价模式的不足，建立了分时段的充电服务费，并进行了相应的价格优化，但同时也存在如下问题：①充电服务费定价方法存在一定的局限性，定价灵活性不高，不能根据负荷的变化及电网的调控需求及时进行服务费调整；②目前大部分充电服务费定价是从电动汽车充电行业的角度进行分地区或运营商的统一定价，针对性不强，难以实现考虑单座充电站具体情况的站级充电服务费调整。

在充电服务费定价灵活性需求不断提高的趋势下，针对上述充电服务费定价存在的问题，本文提出了一种基于智能合约的电动汽车充电服务费自适应调整机制，可以为站级充电服务费定价调整提供有效的指导。基于该充电服务费调整机制，可以使充电站根据负荷的预测情况及电网的调控需求，更加灵活、更具针对性地调整自身的充电服务费定价策略，在考虑用户充电成本的基础上，最大限度地提高自身的收益水平。首先，建立了基于智能合约的充电服务费自动调整机制架构；其次，建立了充电服务费-负荷弹性模型，分析充电服务费调整下用户充电行为的演变；然后，考虑购售电双方的收益及电网的调控需求，建立了充电服务费优化模型，并采用改进粒子群优化IPSO（Improved Particle Swarm Optimization）算法进行迭代寻优，实现充电服务费周期性自适应调整；最后，基于算例进行仿真，从算法效率、负荷引导效果、收益水平3 个方面对所提定价模式、传统统一定价模式进行对比，以验证所提充电服务费调整机制的有效性。

1 基于智能合约的充电服务费自适应调整机制

1.1 智能合约技术

智能合约的概念于1995 年由Nick Szabo 首次提出，其本质是一套以信息化方式进行交易触发、交易执行、交易结算的计算机协议。智能合约具有弱中心化、去信任、不易篡改的特性，能实现不同节点间交易的无差别记录，促进信息的互联互通。智能合约作为“互联网+”新业态的一种新型应用技术，被广泛应用于“高频微量”的电力市场交易、能源需求响应等场景。

基于上述特征，本文提出了一种基于智能合约的电动汽车充电服务费自适应调整机制。合约会根据充电站输入的未来负荷预测信息与电网的调控信息，周期性地自动调整优化充电服务费，将充电服务费调整信息发布给用户以调整用户的充电行为，并根据发布的充电服务费进行交易执行与结算。该机制具有如下特点。

1）充电服务费的调整灵活性更强。可以电网调控信息及负荷预测数据为依据，针对单座充电站实现充电服务费的周期性灵活调整。

2）充电服务费调整的精度更高。摒弃了传统的统一定价模式，而是考虑电网调控信息以及购售电双方的收益水平，针对性地进行充电服务费调整。相较于传统的服务费定价模式，该定价机制下的负荷引导效果更强，能够同时使双方的收益水平提高20.8%。

3）交易效率更高，且实现了电动汽车充电交易全流程的智能化、合约化。规范了电动汽车充电过程中的电力交易行为，保障了电动汽车充电交易的公平、高效执行，可以满足现阶段海量电动汽车接入现状下充电交易与服务费调整的需要。

1.2 基于智能合约的充电交易架构

充电站根据负荷调控平台的调控需求及负荷预测情况，调整自身的充电服务费，用户根据充电服务费的变化调整自身的用电行为，并根据当前的充电服务费与充电站签订充电合约。基于智能合约的充电服务费调整总体架构如图1所示。

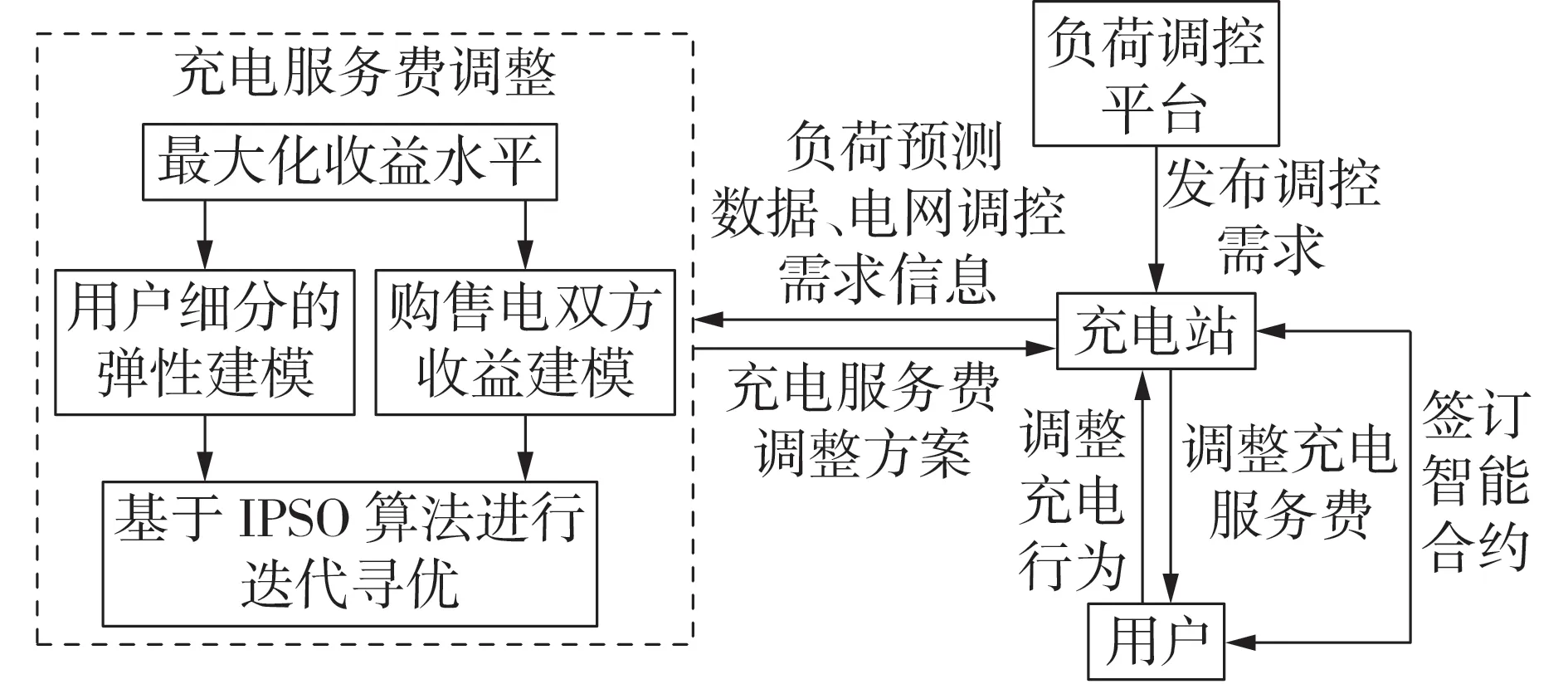
图1 基于智能合约的充电服务费调整总体架构Fig.1 Overall framework of charging service fee adjustment based on smart contract

运用智能合约技术能保障在灵活调整充电服务费的情况下交易的便捷程度及交易效率，为海量电动汽车接入下充电服务费的灵活调整提供技术支撑。智能合约的结构及签订流程如图2所示。

图2 智能合约的结构及签订流程Fig.2 Structure and signing process of smart contract

1.3 基于智能合约的充电服务费自适应调整具体流程

基于智能合约的充电服务费自适应调整共分为3 个模块展开，如图3 所示，具体的自适应调整步骤如下：

图3 基于智能合约的充电服务费自适应调整框架Fig.3 Framework of adaptive adjustment of charging service fee based on smart contract

1）通过智能合约采集未来电动汽车充电负荷的预测数据、基础负荷数据以及电网的调控需求；

2）根据充电服务费-负荷弹性模型，结合用户电动汽车充电负荷的预测数据，定量分析充电服务费变化对负荷的影响程度，建立充电服务费与负荷之间的函数对应关系；

3）对用户与充电站的收益进行建模，分析不同负荷状态下用户与充电站的收益情况，建立用户收益、充电站收益与负荷之间的函数对应关系；

4）经过步骤2）和步骤3），可得到不同充电服务费下的加权收益，以加权收益最大化为目标，并采用IPSO算法进行迭代优化，求解最优定价策略；

5）发布未来各时段充电服务费的调整策略，用户进行自身充电行为调整，智能合约根据充电服务费撮合充电站与用户进行电量交易，并根据交易信息进行自动执行与结算。

2 基于用户细分的电动汽车负荷弹性建模

本节运用弹性理论，定性分析充电服务费调整对充电负荷的影响。虽然单辆电动汽车的充电行为具有很强的随机性，但是同一充电偏好类型的电动汽车用户群体的响应行为往往呈现一定的规律［17］。因此，本文在用户细分的基础上，建立充电服务费-负荷弹性模型，用于分析充电服务费变化对用户充电负荷的影响程度。

2.1 充电服务费-负荷弹性模型

电动汽车充电服务费的变化会在一定程度上引导用户改变自身的充电行为。将1 d以1 h为间隔分为24 个时段，为了分析各时段充电服务费变化对用户充电行为的影响程度，本文引入了充电服务费-负荷弹性函数ε，如式（1）所示。

式中：εi-j（i，j=1，2，…，24）为时段i的充电服务费变化对时段j充电负荷的弹性系数；mj、Δmj分别为时段j电动汽车的充电负荷量及其变化量；pi、Δpi分别为时段i的充电服务费及其变化量。

充电服务费矩阵p、充电负荷矩阵M分别为：

式中：M0为充电服务费调整前的充电负荷矩阵；p0、p分别为调整前、后的充电服务费矩阵。

2.2 基于用户细分的充电服务费-负荷弹性模型

不同用户对充电服务费变化的响应情况不同，仅将用户看作一个同质的整体进行分析可能会导致结果不准确［18］。为此，本文对2.1 节的充电服务费-负荷弹性模型进行改进，根据用户对充电服务费调整的响应积极性，对用户集群进行分类，并分别分析其弹性系数。

按照响应积极性可将用户分为利益导向型用户、便利导向型用户、中庸型用户3类，3种不同类型用户的响应曲线见附录A图A1。

2.2.1 利益导向型用户

利益导向型用户主要为一些充电时间较为宽裕，或者用户自身对充电价格变动较为敏感的用户，如自由从业者。该类型用户的充电服务费-负荷弹性系数εa最大，其会跟据充电服务费的变动，积极地调整自身的充电行为。

2.2.2 便利导向型用户

便利导向型用户主要为一些充电时间较为固定，或者用户只考虑自身用车便利性而不考虑充电价格的用户，如公交车司机。该类型用户的充电服务费-负荷弹性系数εc较大，其基本不会根据充电服务费的变化对自身的充电行为进行调整。

2.2.3 中庸型用户

中庸型用户主要为响应积极性处于利益导向型用户响应积极性与便利导向型用户响应积极性之间的一部分用户。该类型用户的充电服务费-负荷弹性系数εb处于前2 类用户的弹性系数之间，其会调整自身充电电量及充电时间进行一定程度的响应，但其响应程度明显低于利益导向型用户。

对于不同的充电站而言，其所处地区的经济水平、所处地段、电网调控需求不同，电动汽车用户的整体弹性也不同，基于历史数据预测3 种不同类型电动汽车用户的弹性系数以及数量，即可得到该充电站的电动汽车用户对充电服务费的响应行为。3种类型用户的弹性系数整体上满足εa＞εb＞εc。

最终可得到单座充电站的充电服务费p与充电负荷M之间的关系为：

式中：M0l、El（l=a，b，c）分别为类型l用户的预测负荷矩阵、充电服务费-负荷弹性矩阵，l=a 对应利益导向型用户，l=b 对应中庸型用户，l=c 对应便利导向型用户。

3 考虑购售电双方收益的充电服务费优化模型

3.1 目标函数

充电站的定价优化一般以自身收益水平最大化为优化目标，但为了防止充电站恶意涨价，本文模型在充电收益最大化的基础上，进一步考虑了用户的收益水平，并引入收益分配权重a，以保证优化目标的合理性，具体充电服务费的优化目标函数为：

maxw=aw1+(1-a)w2（7）

式中：w为用户和充电站的总收益；w1为用户的净收益；w2为充电站的净收益。为了保证利润分配的合理性，本文设置用户的收益分配权重为a，其取值范围为［0，1］，具体取值由电力供需关系、谈判地位、市场发展阶段等因素综合决定。

3.2 用户的净收益模型

用户的净收益主要来自充电服务费调整前、后电动汽车的充电成本之差，可表示为：

3.3 充电站的净收益模型

3.3.1 电动汽车充电收益

电动汽车在充电站充电并向充电站支付充电费用，电动汽车充电收益是充电站收益的主要来源。电动汽车充电收益主要分为基本电费收益、充电服务费收益两部分，如式（9）所示。

3.3.2 负荷响应补偿收益

充电站聚合站内电动汽车的充电负荷，发掘其调控潜力，引导其参与电网调控响应，从而自电力市场获得相应的响应补偿收益。负荷响应补偿收益主要分为响应容量补偿、响应里程补偿，如式（10）所示。

3.3.3 购电成本

充电站从电力市场购买电量用于站内电动汽车充电，需支付一定的购电成本，其是充电站运行过程中产生的主要成本，计算式为：

式中：ccharge为充电站支付的购电成本；pbt为时段t的购电电价。

3.3.4 偏差考核成本

在电动汽车参与电网响应的过程中，实际响应量与中标量之间会存在偏差，电网会针对该部分偏差进行考核，并根据偏差量进行响应惩罚。偏差考核成本cv可表示为：

3.4 约束条件

3.4.1 电动汽车充电服务费约束

为了防止充电站恶意涨价，需将电动汽车的充电价格控制在合理的范围内，则应对各时段的充电服务费浮动空间进行限制，即需满足：

式中：pt，min、pt，max分别为时段t充电服务费的最小值、最大值，一般由当地政府的政策规定。

3.4.2 用户的净收益约束

调整充电服务费后，应使得用户的充电成本相较于调整前有所降低，即需满足：

3.4.3 配电网容量约束

受充电站所在地区配电网容量的限制，基础负荷与充电站充电负荷之和需小于配电网变压器的最大可用容量，即：

式中：mr，t为时段t充电站所在配电网的基础负荷；mmax，t为时段t配电网变压器的最大可用容量。

3.5 基于IPSO算法的定价合约求解流程

粒子群优化（PSO）算法是一种模拟鸟类进食进行迭代寻优的全局寻优算法。PSO 算法作为启发式算法，其收敛速快，对目标函数的格式要求不严格，适用于求解充电服务费定价这类复杂非凸的优化问题。同时，传统PSO 算法的求解过程存在易陷入局部最优解的问题。为此，本文提出了一种IPSO 算法，算法的求解流程图如图4所示。

图4 基于IPSO算法的定价合约求解流程图Fig.4 Flowchart of solving pricing contract based on IPSO algorithm

模型的输入为电动汽车预测充电负荷及弹性矩阵，算法的求解步骤如下：首先，将每个粒子作为1 组充电服务费方案，初始化粒子信息，包括初始位置X、初始速度V、惯性权重ω；然后，以用户和充电站的总收益最大化作为适应度函数，寻找最优粒子，并对全局粒子进行迭代，直至算法收敛得到最优解。在迭代过程中，对部分粒子的历史最优位置与当前位置进行交叉操作，扩大了PSO 算法对多维度问题的求解广度，同时每个粒子根据其历史最优值按照差分算法的自适应策略进行变异操作，有利于粒子跳出局部最优区域，以保证最终结果的全局最优性。IPSO 算法在寻优迭代过程中的计算公式见附录B式（B1）—（B5）。

4 算例仿真

4.1 算例介绍

本文选取某地区1 000 辆电动汽车接入情况下充电站的负荷情况为算例，运用MATLAB 进行仿真分析。电动汽车的负荷曲线采取2021年3月电动汽车的日负荷预测数据，电动汽车充电服务费-负荷弹性矩阵E见文献［19］，分别从算法优化效率、负荷引导效果、购售电双方收益水平对如下3 种情景进行分析：①情景1，采用固定的分时段充电服务费（取自2021 年3 月海南的充电服务费数据）；②情景2，采用基于PSO 算法优化的充电服务费定价；③情景3，采用基于IPSO 算法优化的充电服务费定价。情景1 采用固定的分时段充电服务费，是目前采用最广泛的定价方式。情景2在情景1的基础上，采用传统的PSO 算法对充电服务费进行优化定价。情景3为本文所提基于智能合约的电动汽车充电服务费调整方案，以加权总收益最大化为目标，并采用IPSO算法对最优充电服务费进行迭代寻优。

4.2 优化流程

本节主要针对情景3，该情景下充电服务费的具体优化步骤如下。

步骤1：获取用户的充电负荷数据以及电网的调控需求作为模型输入，具体见附录C图C1。

步骤2：分析充电站的充电服务费-负荷弹性。以文献［19］中的弹性矩阵E作为基础数据，充电站内3 种不同类型电动汽车用户的弹性矩阵以及数量如表1 所示，以此为基础计算充电站的充电服务费-负荷弹性。

表1 充电站内不同类型电动汽车用户的弹性矩阵及数量Table 1 Elasticity matrix and quantity of different types of electric vehicle users in charging station

同时为了简化计算，将一天24 h 划分为峰、谷、平3 个时段，则24×24 阶弹性矩阵被简化为3×3 阶矩阵，对于分别转移至峰、谷、平3 个时段的总负荷量，可按照各单位时段内的负荷大小比例进行分配。

步骤3：分析用户和充电站的收益情况。根据第3 节中用户和充电站的收益模型，分别分析用户和充电站的收益情况，其中设定用户的收益权重a的取值为0.5。

步骤4：运用IPSO 算法对充电服务费进行优化。根据3.5节的充电服务费优化模型的求解步骤，以加权收益最大化为目标，对充电服务费进行自适应优化调整。

在优化过程中，不同阶段粒子的收敛水平如图5 所示。在迭代初期，由图5（a）可以看出，生成的充电服务费方案在可行空间内随机分布；在进行第500 次迭代时，由图5（b）可以看到，绝大部分方案已经逼近最优解［0.80，0.43，0.12］元／（kW·h）。

图5 充电服务费的优化迭代结果Fig.5 Optimization iteration results of charging service fee

4.3 结果分析

本节将根据优化后的结果，从算法优化效率、负荷引导效果、购售电双方收益水平3 个角度，对本文所提基于智能合约的充电服务费自适应调整机制的优化效果进行具体分析。3 种情景的最终充电服务费定价结果如表2所示。

表2 3种情景的最终充电服务费定价结果Table 2 Final pricing results of charging service fee for three scenarios

1）算法优化效率对比分析。

在算法优化效率方面，情景2 采用的传统PSO算法及情景3采用的IPSO算法的优化效果对比如图6 所示。由图可以看出：在算法收敛速度方面，IPSO算法的收敛速度更快，在第500 次迭代过程中即达到最优解，相较于传统PSO 算法，迭代速度提高了60%；在最优解方面，IPSO 算法通过改进使迭代可跳出局部最优解，最终的最优总收益为16421.67元，相较于传统PSO算法所得局部最优解对应的总收益15867.62元，其收益水平提高了3.50%。

图6 优化算法的效果对比Fig.6 Effect comparison of optimization algorithms

2）负荷引导效果对比分析。

在上述最优的充电服务费定价策略下，3 种情景的电动汽车充电负荷曲线如图7 所示。由图可知，情景2、3 对充电服务费的优化调整均使电动汽车充电负荷在一定程度上响应了电网的调控需求。但从响应效果来看，相较于情景2，情景3 的负荷响应效果更加明显，有3%～6%尖峰与高峰时段的负荷被转移到了平时段与谷时段，降低了电动汽车充电负荷的峰谷差，进而减少了电动汽车无序充电对电网运行产生的压力。

图7 3种情景的电动汽车充电负荷曲线Fig.7 Charging load curves of electric vehicles for three scenarios

3）购售电双方收益水平对比分析。

3 种情景下用户和充电站的收益见表3。由表可以看出，通过情景2 与情景3 中2 种算法调整不同时段的充电服务费，用户和充电站的总收益均有所提升。相较于情景2，情景3中用户获得的收益略低，但从用户和充电站的总收益来看，本文所用IPSO 算法使总收益提升了3.50%，验证了IPSO 算法的优化效率。

表3 3种情景的用户和充电站收益对比Table 3 Comparison of users’and charging station’s benefit for three scenarios

4.4 敏感性分析

1）充电服务费峰谷差。

充电服务费峰谷差变化对总收益变化的敏感性分析结果如表4 所示。由表可以看出：当充电服务费峰谷差在±10%范围内变动时，总收益随电动汽车充电服务费的变化呈正线性相关变化，说明在一定的范围内放开充电服务费的定价限制，有利于提高社会总收益水平；当充电服务费峰谷差上调超过15%后，总收益反而出现了一定程度的下降，这是因为峰谷分时电价差过大会使大量的负荷从峰时段转移至谷时段，造成负荷的“反调峰”现象，进而对社会总收益产生不利的影响。

表4 充电服务费峰谷差对总收益的敏感性分析Table 4 Sensitivity analysis of peak-valley difference of charging service fee to total revenue

2）用户响应弹性系数。

用户响应弹性系数对总收益变化的敏感性分析结果如表5 所示。由表可以看出，总收益随着弹性系数的增大而增大。但随着弹性系数的不断上调，总收益的增大趋势有所减缓，这是因为当弹性系数进一步提高后，用户的响应积极性不断增加，使得迭代所得最优充电服务费降低，进而影响了充电站的收益。

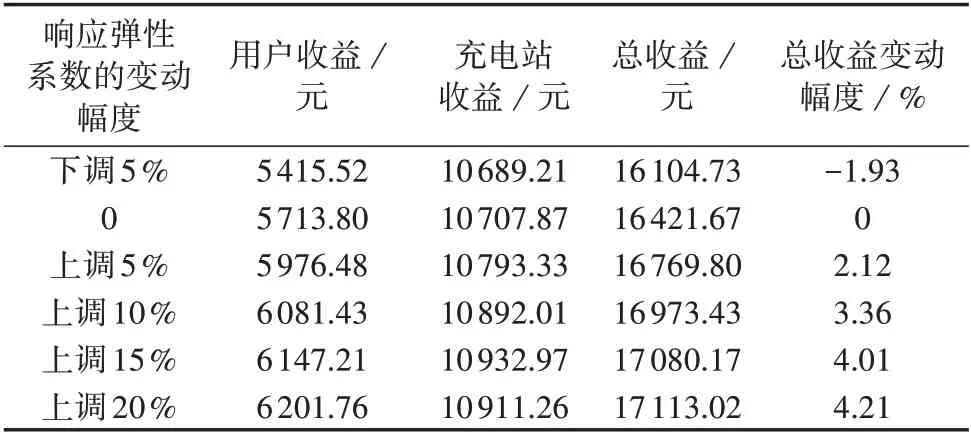
表5 用户响应弹性系数对总收益的敏感性分析Table 5 Sensitivity analysis of user response elasticity coefficient to total revenue

综合上述分析可知，在一定的范围内提高充电服务费峰谷差以及用户响应弹性系数，可进一步提高用户和充电站的总收益，其中提高充电服务费峰谷差的措施包括进一步放开充电服务费定价限制、提高尖峰电价等，提高用户响应弹性系数的措施主要包括培育用户的错峰用电意识、完善有序充电利润传导机制。相关措施的有效实行，将进一步提高社会的总收益水平。

5 结论

本文针对传统集中式充电服务费定价难以满足新型电力系统需求的问题，建立了一种基于智能合约的电动汽车充电服务费调整机制，运用智能合约技术可针对不同的充电站制定更加灵活、更具精确性的充电服务费调整策略。

针对不同类型的响应用户，建立了电动汽车用户细分的充电服务费-负荷弹性模型，进而更加精确地分析电动汽车充电服务费调整对负荷变化的影响程度；同时对用户及充电站收益进行建模，以加权总收益最大为目标，并采用IPSO 算法对模型进行求解。

基于算例从优化定价、算法优化效率、负荷引导效果、购售电双方收益水平对本文所建模型的有效性进行验证，结果表明：相较于传统的统一定价模式，所提充电服务费调整机制下，总收益由13 652.61 元提高为16 421.67 元，同时实现了将4%～8%高峰时段负荷转移至低谷时段；在算法优化效率方面，相较于传统PSO 算法，本文所用IPSO 算法的收敛速度提高了60%，优化后的总收益水平提高了3.50%，验证了所提机制对收益水平提升及负荷引导两方面皆具备显著优势。同时进行了敏感性分析，结果表明在一定的范围内提高充电服务费峰谷差、用户响应弹性系数，可进一步提高用户及充电站的总收益，并针对性地提出了包括进一步放开充电服务费定价限制、提高尖峰电价、培育用户错峰用电意识、完善有序充电利润传导机制等可提高充电交易双方总收益水平的相关政策建议。

附录见本刊网络版（http：//www.epae.cn）。