基于ARM SVE的FFT算法向量化研究

李凤娇，顾乃杰，齐东升，苏俊杰

(中国科学技术大学 计算机科学与技术学院，合肥 230027)

(中国科学技术大学 安徽省计算与通信软件重点实验室，合肥 230027)

E-mail：lfj@mail.ustc.edu.cn

1 引 言

快速傅里叶变换[1]是计算离散傅里叶变换(Discrete Fourier Transform，DFT)的快速算法.FFT将DFT的计算复杂度从O(N2)降低到O(NlgN)，对信号处理技术有变革性的影响，并且被广泛应用于图像处理、微分方程求解、分子动力学等科学领域.现有的FFT的优化研究主要包含针对特定处理器平台的软件优化[2-4]，面向不同平台的自适应优化[5，6]，以及FFT计算过程的改进[7，8]等.其中，张杰等人[2]，杨振浩等人[3]和王小乐等人[4]针对特定处理器对FFT进行向量化优化，LI等人[5]和李炎等人[6]设计了代码自动生成的自适应框架，Doru等人[7]和陈海燕等人[8]优化FFT计算过程的内存访问和存储结构，均取得了很好的效果.

SVE[9，10]是ARM公司推出的基于ARMv8-A体系架构的SIMD技术，主要面向高性能计算，机器学习等领域.不同于现有的SIMD架构，SVE并未固定向量寄存器的位宽，而是可以选择从最低128位到最高2048位的位宽(要求是128的倍数).SVE支持向量长度无关的编程模型，在向量长度不同的硬件架构中运行相同的二进制文件而不需要重新编译，基于SVE编写的程序具有很好的可移植性和灵活性.此外，SVE还引入了每通道预测，谓词驱动的循环控制，非线性访存，复数操作指令，水平归约指令等架构特性，以实现高效的数据并行.

截止目前有关FFT算法在SVE上的研究很少，Takahashi[11]基于编译器自动向量化和代码自动生成框架SPIRAL将Fortran库FFTE移植到富士通A64FX处理器中，并取得了很好的性能提升.目前利用SVE的架构特性进行FFT算法的改进仍有较大的研究空间.本文致力于充分利用SVE的向量长度可扩展性，结合循环控制，非线性访存，复数操作等特性，提出了高效的FFT实现算法，与FFTW库基于Neon的实现相比，取得明显性能提升，在向量长度为1024位时，平均性能提升为5.83倍，最高性能提升可以达到9.22倍.

2 背景介绍

2.1 ARMSVE概述

ARMSVE是ARMv8-A架构A64指令集在AArch64执行模式下的向量扩展，支持128位到2048位的向量长度，和ARM传统的位宽为128位的NEON架构相比，具有更高的数据并行性.作为ARM处理器新一代SIMD的关键技术，SVE能够解决高性能计算，机器学习，数据分析等日益增长的计算需求.SVE的VLA编程模型使得程序编译生成的二进制文件能够动态适应处理器的向量长度.因此，CPU供应商可以根据目标工作负载选择合适的向量长度，以满足用户不同的性能功耗需求.

SVE提供了32个可伸缩向量寄存器，16个谓词寄存器，1个容错寄存器和一组控制寄存器，其中，谓词寄存器是SVE扩展的核心，是支持VLA特性的关键.谓词寄存器作为向量寄存器的掩码，也是可伸缩的，其长度是向量寄存器的1/8，每一位对应向量寄存器的一个字节，用于控制每个通道的活性，1表示对该通道执行操作，0表示不执行操作，即每通道预测.谓词寄存器驱动的循环控制能够在循环中更新谓词，防止访问越界，省去尾部处理，从而支持循环的向量长度无关执行.

2.1.1 复数操作指令

SVE引入了一组复数操作指令，包含浮点指令fcadd，fcmla和整形指令cdot等.这些指令的输入和输出均为向量寄存器，其中偶数序号通道为实部，奇数序号通道为虚部.本文基于复数操作指令实现了FFT算法，将复数的实部和虚部连续地加载到寄存器中，能够执行与算法逻辑一致的复数运算.使用复数乘加指令fcmla计算复数向量乘法需要两条指令：

fcmla z3.d，p0/z，z1.d，z2.d，#0

fcmla z3.d，p0/z，z1.d，z2.d，#90

表示将向量寄存器z1和z2的复数乘法结果累加到z3中，其中，p0是控制元素活性的谓词寄存器，#0，#90为旋转立即数，取值为0，90，180，270，表示将第2个源寄存器的复数元素做旋转，不同的立即数组合能够计算复数乘加，复数乘减，共轭复数乘等结果.

2.1.2 非线性访存

SVE提供丰富的寻址模式和非线性访存模式，引入了一组聚集取(gather-load)和分散存(scatter-store)指令，支持标量基址组合向量偏移，或向量基址组合标量偏移的寻址模式.以标量基址组合向量偏移为例：

ld1d z0.d，p0/z，[X，z1.d]

表示将内存基址为X，向量偏移为z1的数据聚集取到z0中.

2.1.3 SVE的C语言扩展

SVE指令集的ARMC语言扩展(ARM C Language Extensions，ACLE)[12]定义了SVE在C语言级别的一组数据类型和函数接口，用于在高级语言中显式地使用SVE指令，C/C++编译器能够将其转换为SVE汇编.ACLE函数与SVE指令的映射不是完全一一对应的，因为指令集架构的某些细节可以由编译器解析.本文FFT算法是基于ACLE实现的.

2.2 FFT算法

FFT算法是高效计算DFT的算法，DFT的定义[1]如下：

(1)

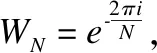
(2)

因此，原始DFT的计算复杂度为O(N2).

FFT算法将DFT的计算复杂度降低到O(NlgN)，经典的Cooler-Turkey算法采用分治策略，对长度为N的输入序列，假设N=rk，r为基，根据旋转因子的周期性和对称性，将DFT分解成r个规模为N/r的子序列的DFT作蝶形运算的结果，迭代k次得到最终结果.算法1示意的是基-rFFT的算法流程.

算法1.基-rFFT算法流程

Input：x，N

Output：X：=FFT(x)

Initial：p=N/r，q=1

1.Reverse(x)

2.forstage=1 to logrNdo

3.forsection=0 topdo

4.forbutterfly=0 toqdo

5. calculate a butterfly kernel of sizer

6.endfor

7.endfor

8.p/=r

9.q*=r

10.endfor

算法1可以抽象成三重嵌套：层-段-蝶形(stage-section-butterfly)[13]，一个N点的基-rFFT可以分解为logrN层，每层划分为不同段，一个段中包含若干个大小为r的蝶形网络，称为基-r的蝶形计算核心，以基-4算法为例，其蝶形结构如图1所示.每个输入因子需要首先乘上对应的旋转因子，然后做蝶形核心计算，得到输出结果.

图1 基-4FFT蝶形计算核心图Fig.1 Butterfly kernel of radix-4 FFT

3 FFT算法的优化

FFT算法包含蝶形网络计算和旋转因子计算两个关键部分，蝶形网络计算是访存密集型和计算密集型操作，主要考虑提高计算访存比，提高并行度的优化方法.旋转因子通常在预处理中进行，本文结合SVE扩展的特性，提出了一种实时计算的方法，缩减预处理时间的同时提高了访存的空间局部性.

3.1 蝶形网络向量化

以基2-FFT算法为例，图2所示为8点FFT的运算过程，一个8点FFT被分解3层，虚线框框出的部分表示一个段，一个段中包含的蝶形互相独立，相邻的蝶形输入和输出内存地址原址连续，因此蝶形网络是SIMD友好的，可以使用SVE提供的向量寄存器，实现数据级并行.

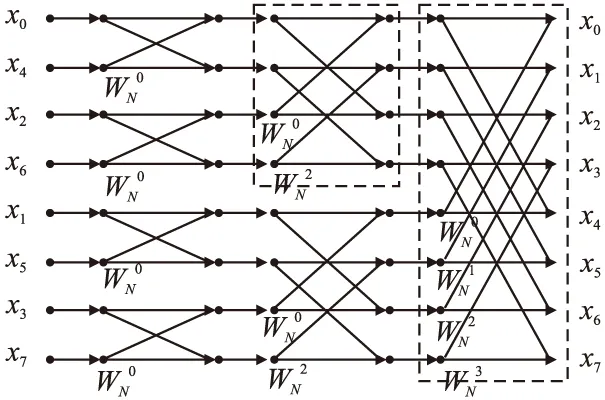
图2 8点基2-FFT蝶形运算Fig.2 Radix-2 FFT butterfly calculation of 8-point

蝶形计算的访存次数与基的大小相关联，对于相同的数据规模，基扩展m倍，算法层数缩减1/m，访存次数相应缩减至原来的1/m.Takahashi的研究[14]表明，FFT算法采用的基增大，需要的复数乘法操作和访存操作均减少，计算访存比显著提升.考虑向量寄存器的数量限制，基-r核心计算所需的向量寄存器可分为4组，分别是输入数据r个，旋转因子r-1个，输出数据r个和临时变量，临时变量包含蝶形计算中间结果r·(log2r-1)个，以及复数乘加指令fcmla的中间变量r-1个.为了使用尽量大的基，需要设计合理的寄存器复用方式以最大限度的利用寄存器资源.

蝶形计算的第1步是计算输入数据和对应旋转因子的乘积，其结果存入输入数据寄存器中，故而旋转因子所占用的寄存器可以复用.蝶形运算中间结果之间存在依赖关系，使用的寄存器可以缩减为2r个，复数乘加指令的中间变量可被复用.输出数据可以复用输入数据所使用的寄存器.因此基-r核心共计使用3r个寄存器.已知SVE架构提供32个可变长向量寄存器，故基取8最为适宜，此时一次蝶形核心使用24个寄存器，可以进行较好的软流水优化.本文以基-8算法为依据，当数据规模N不是8的幂时，使用Cooley-Turkey算法，将N分解成2·8m或4·8m的形式进行边界处理.

SVE扩展的向量寄存器长度为128位-2048位，每个向量寄存器能够存储1-16个双精度复数.利用SVE指令集特有的复数操作指令，使用2条fcmla指令计算一次向量复数乘法，使用1条fcadd指令计算复数向量乘i的结果，进一步减少了指令数.在向量化后，每个蝶形单元能够同时完成1-16个蝶形运算，一个蝶形单元需要24条访存指令，21条复数浮点乘加指令，24条浮点加减指令，计算访存比为15:8.3.2节提出的方法将进一步使用浮点操作替代访存操作，提高计算访存比.算法并行度随着向量长度扩展而提高，向量长度每扩大一倍，其核心循环次数减少约50%，因此指令数大幅度减少.

3.2 旋转因子计算优化

现有的FFT实现大多在预处理步骤生成旋转因子表，在蝶形计算阶段读取所需的数据，本文依据SVE丰富的寻址模式和复数操作特性，利用旋转因子的对称性和周期性，简化旋转因子的实时计算，使用计算操作替代访存操作，无需提前计算并存储旋转因子，具有更好的空间局部性.在FFT算法中，每一层的所有段共用一组底数相同的旋转因子.基-8算法的第L层所需的旋转因子如表1所示.其中，M=8L为旋转因子的底数.蝶形单元的8组旋转因子分别记为w0，w1，…，w7，可以看出，wi=wi-1·w1，2≤i≤7，因此，只需要读取w1，根据w1计算出w2，…，w7，使用2条复数乘加指令取代1条load指令，进一步提高了计算访存比，优化了软件流水.下一步考虑如何在循环中存储和更新w1.

表1 基-8FFT第L层旋转因子表Table 1 Radix-8 twiddle table of the stage L

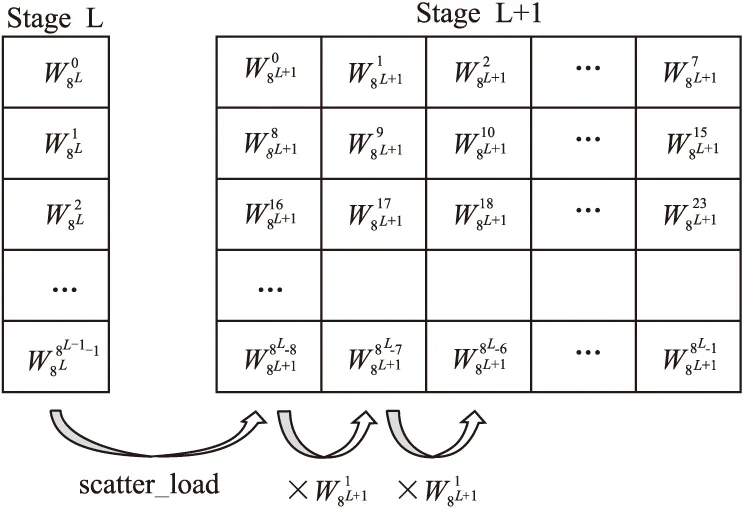
图3 第L层到第L+1层的旋转因子计算步骤Fig.3 Twiddles conversion from stage L to stage L+1

3.3 位反数压缩存储

FFT算法在执行前需要位反序重置，本文采用读表法，在预处理阶段计算位反数，在执行阶段加载位反数.由于FFT算法第1层的旋转因子均为1，不需要乘旋转因子，并且位反读取和第1层计算结合能够减少两次I/O操作，因此将第1层单独计算.与3.1描述的向量化不同，第1层的每个段只有一个蝶形，相邻蝶形单元的输入和输出均不连续，所以在段的维度做SIMD向量化，利用gather-load读取位反数下标对应的非连续输入数据，利用scatter-store将结果输出到步长为16的内存地址中.

考虑位反数的压缩存储，首先，将0～N-1(=8k-1)按序分为8组，0～8k-1-1，8k-1～2·8k-1-1，…，7·8k-1～8k-1，可以证明，后一组的位反数是前一组的位反数加1.因此只需计算第1组位反数，位反数数组大小压缩至N/8.其次，每连续8个数的位反数对应的输入数据组成一个蝶形单元，可以推导出，每连续8个数的位反数是一个等差为N/8的等差数列.因此只需计算每个蝶形第1位下标的位反数，故位反数数组大小压缩至N/64.由此计算的位反数数组在复数数组中的实际偏移量恰好对应了上述gather-load的操作数，这么做同时为向量化提供了便利.

3.4 边界处理

当数据规模N不是8的幂时，根据Cooley-Turkey算法，将N分解成2·8m或4·8m的形式，即将原N点DFT转化成独立的b点FFT和8m点FFT，其中b∈{2，4}.将输入数据按列优先方式映射成8m×b维矩阵，第1维的8m点FFT是内存连续的，可以调用前述优化的基-8FFT，第2维b点FFT是非连续的，可以按列向做SIMD优化，并将结果乘上旋转因子，旋转因子使用3.2节描述的浮点计算代替访存的方法计算.为了充分利用计算资源，对b点FFT进一步做循环展开以增加指令流水.由于最终结果需要按行主序输出，为避免转置操作，将基-8FFT最后一层单独计算，使用scatter-store存入步长为b的输出地址，节省了两次I/O操作.

4 实验及分析

目前支持ARMSVE的硬件平台尚未普及，本文针对双精度复数一维FFT，采用ARMIE模拟器[10]对算法进行验证和指令计数，采用gem5模拟器[15]对性能进行评估.

ARMIE是ARM官方开发的SVE模拟和分析工具，能够将SVE指令转换成原生ARMv8-A指令，通过选项-msve-vector-bits指定运行时向量长度，支持二进制文件的动态执行，并提供指令计数，内存跟踪等功能，ARMIE需要运行在ARMv8-A架构的AArch64平台上.图4展示了数据规模为2048，4096，8192时不同向量长度下的SVE指令计数，可以看出，SVE指令数呈指数下降趋势，表明SVE扩展向量寄存器能够有效地提高并行度.

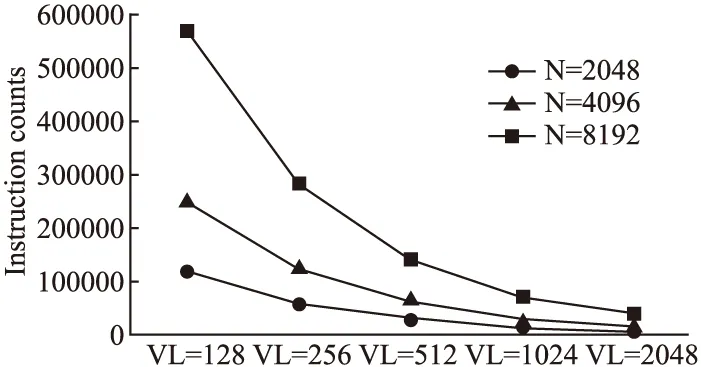
图4 双精度复数FFT的指令计数Fig.4 Instruction countsofdouble-precision complex-to-complex FFT

gem5模拟器是一个开源的高度可配置的模块化通用体系架构模拟器，支持多种处理器架构，在学术界和工业界都有广泛的应用.gem5提供不同的CPU模型，系统模型和内存模型，因此具有高度的灵活性.gem5包含两个主要的CPU模型，原子模型和O3模型.原子模型提供指令级别的模拟，是一种有序非流水线模型，O3模型能够模拟乱序流水线，精确的估计执行指令周期.本实验基于O3模型，表2为本文配置的模拟器环境.

表2 gem5模拟ARMSVE的规格参数Table 2 Specifications of gem5 for ARM SVE

实验使用的编译器是gcc10.1.0，在编译时需要添加编译器选项-march=Armv8-a+sve用于配置ARMv8SVE架构.在相同环境下将本文算法与FFTW3.3.8针对ARMNeon指令集的优化实现进行了对比，图5描述了双精度复数FFT在FFTW以及SVE不同向量长度下的性能对比.复数FFT的性能计算公式[16]为：

图5 双精度复数FFT的性能对比Fig.5 Performance comparison of double-precision complex-to-complex FFT

(3)

其中，runtime是以微秒为单位的运行时间.

向量寄存器长度128位时，性能是FFTW的0.985～1.166倍，在N=1024，2048，8192时，性能略低于FFTW，造成该结果的原因主要有两个，一方面是因为FFTW实现了2，4，8，16，32，64，128点FFT的高效直接展开，在计算时依据Cooley-Turkey分解原则直接调用，如将2048点FFT分解成了64点FFT和32点FFT.另一方面，SVE的向量长度未知性导致向量寄存器的内存是动态分配的，寄存器对堆栈的读写造成了一定的性能损失.本文致力于利用SVE的向量长度未知性和架构特性，改进FFT算法的实现，主要是挖掘基于SVE的软件可扩展性和可移植性，同时也为硬件选择提供了灵活性，能够根据性能，功耗，工作负载等需求定制处理器.本文采用的基-8算法有利于扩展到通用的基-radix算法中.

在扩展的向量长度下，性能均取得明显提升，位宽为256时，平均性能提升2.06倍，最高性能提升3.06倍；位宽为512时，平均提升3.62倍，最高提升5.52倍；位宽为1024时，平均提升5.83倍，最高提升9.22倍.一方面，对于相同的向量长度，数据维度越大，性能提升越高，这是因为与本文的算法相比，FFTW采用的分解策略在数据维度较大时访存局部性低，分解转置导致访存操作增多.另一方面，对于相同的数据规模，随着向量位宽扩大，性能的增幅逐渐减小，这是因为虽然SVE指令数降低，但非向量指令的存在导致SVE指令数在总指令数中的占比下降，故性能增幅下降.

在Intel处理器上，官方提供的数学核心库[17](MathKernelLibrary，MKL)的FFT模块性能通常优于FFTW库，为进一步验证本文算法的有效性，在单核处理器上将本文算法在gem5模拟器上的效率与IntelMKL的效率进行比较，效率的定义为：

(4)

MKL实验的硬件平台为Intel(R) Xeon(R) E5-2690 v3处理器，频率为2.60GHz，支持256位的AVX2向量扩展，图6描述了MKL与256位-SVE的效率对比.可以看出，本文算法的性能较为平稳，在数据规模小于8192时效率更好，MKL在数据规模较大时更具优势.因此，算法在较大数据规模下还有待进一步改进.

图6 MKL-AVX2与256位-SVE效率对比Fig.6 Efficiency comparison of MKL-AVX2 and 256-bit-SVE

5 结 论

FFT算法在通用CPU上的优化工作已经取得了很大的进展，但是在ARMSVE上的相关研究工作较少.本文结合SVE的VLA编程模型，非线性访存，复数操作等相关特性，辅以减少访存，循环展开，提高空间局部性等常见性能优化方法，对FFT算法做向量化展开，并提出了旋转因子计算优化的FFT算法，比较分析了在不同向量寄存器位宽下的性能表现，验证了SVE的可扩展性带来的性能提升.实验表明，在不同向量长度下，该算法和FFTW相比取得了明显的性能提升，在位宽为1024时，平均性能提升5.83倍，最高提升达到9.22倍.目前SVE的软硬件开发尚未普及，因此本文的研究对SVE在高性能计算中的应用具有一定的指导作用.

接下来的工作将对本文的工作进行扩展，研究通用的不同基的FFT算法，构建分解策略以实现非2的幂次FFT计算.