标签松弛回归的跨模态哈希检索

庄智钧，滕少华，张 巍，滕璐瑶

1(广东工业大学 计算机学院，广州 510006)

2(广州番禺职业技术学院 信息工程学院，广州 511400)

E-mail：shteng@gdut.edu.cn

1 引 言

近年来随着网络技术的提升及多媒体数据的爆炸性增长，使得我们在现实生活中要面对的数据量越发庞大，同时，我们目前的需求不再满足于单一模态数据的相似性检索，而是多模态数据间的相互检索，即跨模态检索.它可以使用一种模态的样本来获得另一种模态的相关结果.在多媒体领域，跨模态检索的应用很广，引起了不小的关注[1-3].在大型数据库中，传统的比较搜索方法由于时间和存储成本高昂，导致现有计算设备几乎不可能对大型多模态数据执行精确搜索.而哈希技术的出现大大降低了检索时间与存储成本，由于其在跨模态检索中的高效率和高准确率，因此在近年来也引起了广泛的关注与应用.哈希学习是将实例的数据点编码成二进制码，即哈希码，以此原始特征之间的距离可以用汉明距离来计算.而待检索的样本则通过哈希函数将原始特征向量映射到汉明空间中，并通过汉明距离进行相似性检索.这样，哈希码能减少存储量并通过位操作来提高检索速度，因此哈希检索技术还具有高效性和灵活性的特点.

最早出现的哈希方法是单模态哈希方法[4-6]，它们专注于从单模态数据的特征中挖掘样本之间的联系来学习紧凑的哈希码.现如今，面对大量的多模态数据，我们常用的需求已经演变为用文本检索图片或者用图片检索文本等多个模态的需求，单模态哈希已经不能满足于我们日常生活的需要，因此，近年来许多跨模态哈希方法应运而生[7-9].而根据是否使用标签信息，跨模态哈希方法大致可以分为无监督方法和有监督方法.无监督哈希方法[10-13]通常致力于挖掘原始的异构数据中的相关性，并将获得的相关性保持在被映射的汉明空间里.使用这种方法可以在缺少标签信息的数据中进行哈希学习.与无监督方法不同，有监督哈希方法[14-17]能把标签中的语义相关性保留在哈希码中，使标签中的相关信息得到了利用，因此生成的哈希码更具判别力和准确性.因而近年来，这种有监督的哈希受到了越来越多的关注.代表性的有监督哈希方法包括语义相关最大化哈希(SCM)[14]，离散跨模态哈希(DCH)[16]等.这些有监督方法使用不同的方式将标签的语义信息保留到哈希码中.如语义相关最大化哈希(SCM)通过构造一个语义相似度矩阵，以此将标签的语义信息集成到哈希码学习过程中，并采用松弛策略来解决哈希码的二进制约束，使得模型简单且求解高效，但是该松弛策略也导致了较大的量化误差.如半松弛监督哈希(SRSH)[17]也使用标签的语义信息构造成对相似度矩阵，并把实例的相似性保留在哈希码中，采用半松弛策略来解决NP难的二进制优化问题.SRSH在一定程度上提升了检索的准确性，但仍然存在松弛策略引起的量化误差问题，且训练时间成本高.如有监督离散哈希(SDH)[18]则是直接将哈希码矩阵线性回归到标签矩阵中，以此利用标签的类别信息来生成哈希码，但是这种直接回归的方式会导致拟合效果不佳，因此模型的检索准确率并不高.而可扩展的离散矩阵分解哈希(SCRATCH)[19]则是在SDH基础上通过学习一个子空间矩阵来近似替代哈希码矩阵，从而提高回归的拟合效果.然而这些方法对标签信息的利用都比较单一，如SCM和SRSH只利用了标签的语义信息，SDH和SCRATCH则是只考虑了标签的类别信息，均未充分利用样本的标签信息.另外，由于哈希码是离散的，会导致求解困难，因而大多数哈希方法放宽了原始离散约束，然后以连续方式求解目标函数以加速算法[20]，这会引起较大的量化误差从而导致学习的哈希码准确性降低.为了解决这个问题，比如DCH[16]利用了一种离散优化算法，可以逐位地求解哈希码，却造成了效率相对较低的短板.

为了克服这些缺点，本文提出了一种新颖的有监督哈希方法，称为标签松弛回归哈希，简称LRRH.该方法使用成对相似度矩阵来度量实例之间的相似度，并且采用了半松弛策略来解决原始NP难的二进制优化问题.此外，为了保留标签的类别信息，本文还采用了标签松弛回归项，这使得标签信息能更自由地嵌入哈希码中.最后，本文引入量化误差项，以生成更有效和高质量的哈希码.而在哈希码的求解中，本文的优化算法能离散地一步生成哈希码的所有位.因此，能避免低效和较大的量化误差问题.本文的主要工作可以总结如下：

1)提出了一种新颖的有监督跨模态哈希方法.该方法能更好地利用样本的标签信息，使学习到的哈希码既考虑了标签的语义相似性，也保留了标签的类别信息.

2)在保留标签的类别信息过程中，引入了标签松弛变量矩阵，使得标签矩阵由定值变为区间，增大了标签矩阵的鲁棒性，使得回归拟合效果更佳.

3)在3个公开数据集上进行了广泛的实验.实验结果表明，LRRH有明显的优势.

本文的其余部分组织如下.第2节简要概述了一些相关的工作.第3节详细介绍了提出的方法.第4节报告了实验结果并进行分析，最后是第五节的总结与展望.

2 相关工作

如前所述，有监督哈希方法能够结合语义标签来学习更有效的哈希码.例如，跨模态相似度敏感哈希(CMSSH)[21]通过最大化不同模态的哈希码的相关性来近似原始特征的相似性.但是，CMSSH仅保留不同模态间的相关性，而忽略了模态内的相关性.为了同时保留模态内和模态间的相似性，跨视图哈希(CVH)[22]将单视图谱哈希技术[5]扩展到多视图的情况，并通过最小化哈希码之间的相似度加权汉明距离来学习哈希函数.语义保留哈希(SePH)[15]通过监督信息构造相似度矩阵，并最小化KL散度将语义相似度近似保留在待学习的哈希码中，然后以两步方式学习统一的哈希码和哈希函数.该方法将标签转换为成对相似度，这会导致较高的训练时间复杂度.而语义相关最大化哈希(SCM)[14]通过将语义标签无缝地集成到哈希码学习过程中，从而避免了这种类型的转换过程，并采用松弛策略来解决哈希码的二进制约束，但这会产生较大的量化误差.离散跨模态哈希(DCH)[16]则通过离散循环坐标下降法(DCC)来保持离散约束并逐位迭代生成二进制码.然而，当哈希码位数较多时，这种方式会导致学习哈希码时的低效问题.广义语义保留哈希(GSPH)[23]通过分解标签信息构造的语义相似度矩阵来学习最佳哈希码，然后使用岭回归和核逻辑回归来学习哈希函数.半松弛监督哈希(SRSH)[17]也是使用标签信息来构造相似度矩阵，并引入一个中间表示矩阵来放宽一部分二进制约束，从而解决离散优化问题.但是该方法没有考虑到中间表示矩阵和哈希码矩阵之间的量化误差问题.值得注意的是，大多数有监督方法如SePH，GSPH，SRSH等都将标签信息转换为成对相似度矩阵来嵌入语义信息，却忽略了类别信息，而此类信息对于检索也很重要.

本文主要关注标签信息的充分利用和量化损失问题，为此提出了一种新的有监督哈希方法，该方法不仅考虑到标签的成对语义相似性，还考虑到它的类别信息，这对于生成高质量的哈希码非常重要.

3 提出的方法

本节介绍了所提出的LRRH的细节.本文主要关注图像数据和文本数据的哈希码学习.在不失一般性下，可以很容易将该哈希方法扩展到更多模态.本文使用的主要符号总结在表1中.LRRH的框架示意图如图1所示，LRRH先是通过分解语义相似度矩阵S来学习哈希码矩阵B和中间表示矩阵V，然后通过最小化B和V之间的平方损失以及对V的正交与均衡约束，使得V近似于B，并通过标签松弛回归，进一步学习到V，最后联合哈希函数得到最终的哈希码.

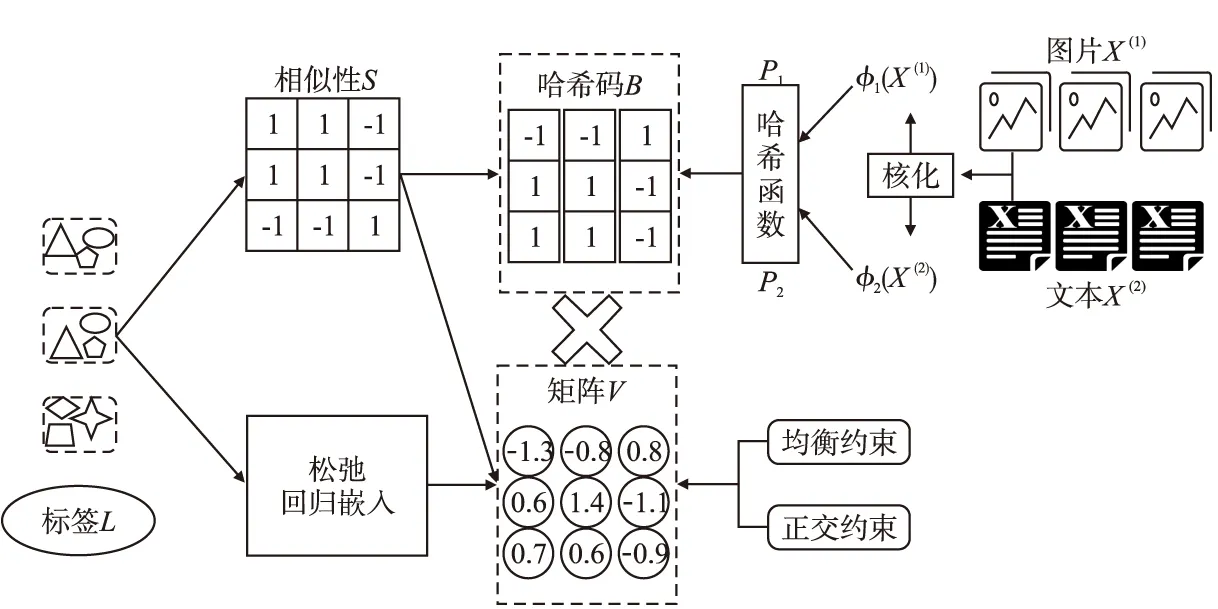
图1 LRRH框架示意图Fig.1 Diagram of LRRH frame

表1 主要符号总结Table 1 Summary of the main symbols

3.1 哈希码学习

3.1.1 成对相似性保留和量化误差最小

为了保证语义相似的标签能学习相似的哈希码，SRSH[17]提出了一种分解相似矩阵来学习哈希码的方法，如式(1)所示：

(1)

其中，S∈{-1，1}n×n是语义相似度矩阵，如果第i个样本和第j个样本在标签语义上是相似的(即至少属于同一个类标签)，则Sij=1，否则Sij=0.V是和B同样大小的中间表示矩阵.通过求解式(1)中的目标函数，哈希码保留了S中的语义相似性.虽然式(1)通过矩阵V替换原来的一个B从而使得原来的离散优化问题得以解决，但是存在这样一个问题：哈希码矩阵B和中间表示矩阵V之间存在一定的量化误差，这在一定程度上会影响学习到的哈希码的质量.

因此，为了减少B和V之间的误差，本文引入量化误差项，并最小化B和V之间的平方损失.此外，为了使学习到的哈希码更有效，本文在哈希码上添加了正交约束与均衡约束，这使得哈希码矩阵列间互不相关，并且每个比特保持平衡[5].式(1)变为式(2)的形式：

(2)

其中η是权衡参数.但是对B这样严格的正交和均衡约束使得优化难以实现.为了解决这个问题，本文通过将约束转移到V来放宽最后两个约束，并将式(2)构造为式(3)形式：

(3)

3.1.2 标签松弛回归

为了更充分地利用标签信息，本文还考虑了用标签的类别信息生成哈希码.SDH[18]提出了一种将哈希码回归到标签以此保留标签类别信息的方法，如式(4)所示：

(4)

矩阵V和哈希码矩阵B具有相同的维度大小，且通过量化误差项以及施加在V上的正交约束与均衡约束，使得矩阵V能近似于哈希码矩阵B，因为哈希码存在二进制约束，直接求解式(4)是困难的，因此，为了便于求解式(4)中的目标函数，可以将中间表示矩阵V替换式(4)中的B，进一步转换为式(5)的形式：

(5)

但是式(5)存在这样一个问题：该方法假定在学习阶段，要将V准确地线性回归到严格的二进制标签矩阵L，但矩阵的自由度太小，这会导致拟合的效果不佳，使学习到的V质量不高.

为了解决这个问题，本文引入标签松弛变量矩阵.

定义1.二元矩阵.二元矩阵D∈Rn×c定义为如下形式：

(6)

定义2.矩阵Hadamard积.设A、Y、C∈Rn×c，如果有：

C=A⊗Y

其中：cij=aij×yij，且aij∈A，yij∈Y，cij∈C.则，⊗为矩阵的Hadamard积.

定义3.标签松弛变量矩阵.设L为一个标签矩阵，且L∈{0，1}n×c，D为一个二元矩阵，M∈Rn×c为非负变量矩阵.则矩阵L的标签松弛变量矩阵定义为：

L°=L+D⊗M

(7)

定义3将严格的二进制标签矩阵L扩展为标签松弛变量矩阵L°，这使L由定值变为区间，增大了L的鲁棒性.

用式(7)中的L°代替式(5)中的L，则有式(8)：

(8)

由式(8)，L°比L具有更大的灵活性，这为V拟合标签提供了更大的自由度，使得拟合效果更好；同时L°扩大了不同类别之间的边距，因而L°比L具有更好的判别力.通过拟合L°，标签中更多的类别语义信息被嵌入到V中，这使标签中的信息得到了进一步的利用，因而，生成的哈希码判别力更强.

3.2 哈希函数学习

对于训练集外的实例需学习哈希函数，并通过哈希函数将实例映射成哈希码，从而进行检索.在学习哈希函数之前将对原始数据进行核化处理，因为核化方法能使机器学习模型更好地适合于非线性可分离数据.核函数可以更好地表达原始特征之间的非线性模态内相关性[24].因此，本文采用RBF核函数，即径向基函数，如式(9)所示：

(9)

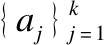
哈希函数的学习可以采用许多分类模型，例如线性分类，支持向量机和神经网络等.一般来说，更复杂的模型可以达到更好的精度，但是，计算成本也可能显着增加.因此，为了平衡准确性和效率，本文采用线性分类器模型来学习哈希函数.具体如式(10)所示：

(10)

其中β是权衡参数，通过最优化式(10)中的目标函数，可以得到相应的投影矩阵Pt.本文定义的哈希函数如式(11)所示：

Ht(x(t))=sgn(φt(x(t))Pt)

(11)

对于训练集外的实例，可以通过式(11)中的哈希函数得到相应的哈希码.

3.3 总体目标函数

LRRH的总体目标函数将式(3)中成对相似性保留项，式(8)中的标签松弛回归项以及式(10)中的哈希函数学习项联合优化，得到式(12)形式：

(12)

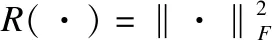
3.4 优化算法

对于6个矩阵变量B，V，M，G，P1，P2来说，目标函数式(9)是非凸的，直接求解非常困难.为了解决这个问题，本文提出了一种有效的迭代优化算法.具体而言，首先使用标准正态分布将B，V，G随机初始化.此后，P1，P2，M，G，V，B交替更新，直到收敛或达到最大迭代次数T.具体的优化过程如下所述.

1)固定B，V，M，G，P2，求解P1，则式(12)可写为：

(13)

展开式(13)并对P1求导，令其导数为零，可以得到闭合解：

P1=(λ1φ1(X(1))Tφ1(X(1))+βIk1)-1λ1φ1(X(1))TB

(14)

同理，

P2=(λ2φ2(X(2))Tφ2(X(2))+βIk2)-1λ2φ2(X(2))TB

(15)

2)固定B，V，G，P1，P2，求解M，则式(12)可写为：

(16)

令U=VG-L，则式(16)可写为：

(17)

根据文献[25]，可以得到M的最优解：

M=max(D⊗U，0)

(18)

3)固定B，V，M，P1，P2，求解G，则式(12)可写为：

(19)

由式(7)并展开式(19)对G求导，令其导数为零，可以得到闭合解：

(20)

4)固定B，M，G，P1，P2，求解V，则式(12)可写为：

(21)

为了解决上述问题，本文把式(21)中的目标函数在约束VTV=nIr，以及B∈{-1，1}n×r下，并由式(7)，转为矩阵的迹的形式，最终简化如式(22)所示：

(22)

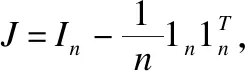
(23)

(24)

5)固定V，M，G，P1，P2，求解B，则式(12)可写为：

(25)

将式(25)转为矩阵的迹的形式，最终简化如式(26)所示：

(26)

因此，式(26)的最优解为：

(27)

因为B具有离散约束，一些方法放宽了二进制约束以生成哈希码，这可能会产生较大的量化误差，而常规离散优化算法使用离散循环坐标下降(DCC)逐位地求解最佳哈希码，从而导致求解B的子步骤中存在许多的迭代.在本文优化算法中，求解B时，哈希码的所有位都可以离散地一步生成，因此效率更高，尤其是在哈希码较长时.算法1总结了LRRH的整个训练过程，包括哈希码学习和哈希函数的学习.

算法1.LRRH的优化算法

输入：图像矩阵X(1)和文本矩阵X(2)，标签矩阵L，哈希码长度r，迭代次数T，图像和文本核化后的特征维数k1和k2，参数γ，λ1，η，β

输出：哈希函数投影矩阵P1，P2和哈希码矩阵B

1.通过RBF核函数分别把X(1)，X(2)映射到核空间

2.用标准正态分布随机初始化B，V，G

Repeat

3.用式(14)和式(15)分别更新P1，P2；

4.用式(18)更新M；

5.用式(20)更新G；

6.用式(24)更新V；

7.用式(27)更新B；

Until 收敛或者达到最大迭代次数

3.5 计算复杂度分析

3.6 多模态的扩展

本文所提出的LRRH中，只考虑了两个模态的情况，即图像和文本.但本文提出的方法也能容易扩展于多模态的情况.假设训练集的实例包含了m个不同的模态，则本文在式(12)中提出的目标函数可以扩展为：

(28)

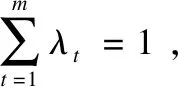
4 实验与分析

为了评估LRRH的性能，本文在LabelMe[27]，MIRFlickr[28]以及NUS-WIDE[29]这3个公开数据集上进行了实验验证，这些数据集已广泛用于跨模态哈希检索文献中，表2总结了3个数据集的统计数据.本文与近年来的无监督图哈希方法FSH[11]，无监督基于矩阵分解的哈希方法CMFH[13]，及有监督的DCH[16]，SCM[14]，SRSH[17]，SCRATCH[19]，GSPH[23]，在用文本检索图像(简化为T→I)和用图像检索文本(简化为I→T)两个跨模态检索任务上进行了性能比较和分析.在实验中，本文使用广泛应用于跨模态哈希算法的评估指标Mean Average Precision(MAP)和精度-召回率曲线(PR曲线)来评估各算法的性能.对于MAP，值越大，结果越好.对于PR曲线，其平均值越高，则表现越好.再者，为了评估所提出方法和所有对比方法的计算成本，本文还对比了它们在不同哈希码长度下的训练时间.

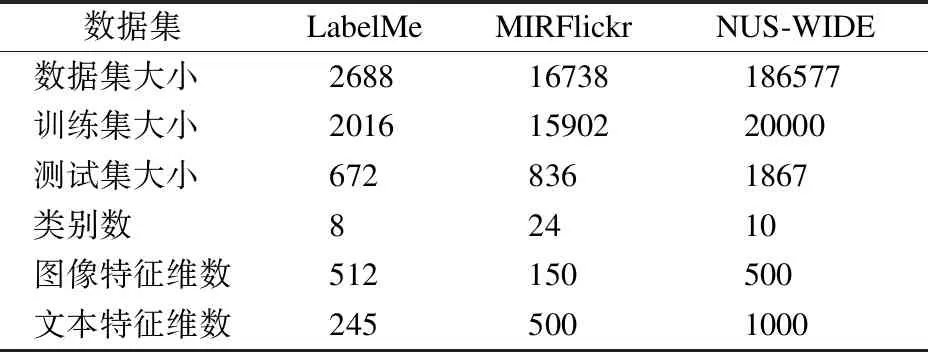
表2 3个基准数据集的统计信息Table 2 Statistical information of three benchmark datasets

4.1 实验设置

所有对比方法由作者提供的代码及其论文中建议的参数来实现.对于LRRH，在所有数据集上，迭代次数T=3，图像数据核化后的特征维数k1=1000，文本数据核化后的特征维数k2=1500.在LabelMe数据集上，各项参数设置为：λ1=0.5，λ2=0.5，γ=10，η=100，正则化参数β=0.001；在MIRFlickr数据集上，各项参数设置为：λ1=0.9，λ2=0.1，γ=1，η=10，正则化参数β=0.01；在NUS-WIDE数据集上，各项参数设置为：λ1=0.2，λ2=0.8，γ=0.01，η=0.01，正则化参数β=0.01；所有实验都在配备Intel(R)Core(TM)i5-9400F CPU@2.90GHz，32GB RAM的机器上进行.

4.2 实验结果及分析

4.2.1 LabelMe数据集的实验结果

表3给出了LRRH和其它对比方法在LabelMe数据集上的MAP结果.它包括图像检索文本和文本检索图像在8～128位不同哈希码长度上的结果.其中最好的结果加粗黑体显示.图2分别绘制了在16位和64位不同哈希码长度下的精度-召回率曲线.

图2 在LabelMe上哈希码分别为16位和64位时的PR曲线Fig.2 PR curves on LabelMe with the code length of 16 bits and 64 bits

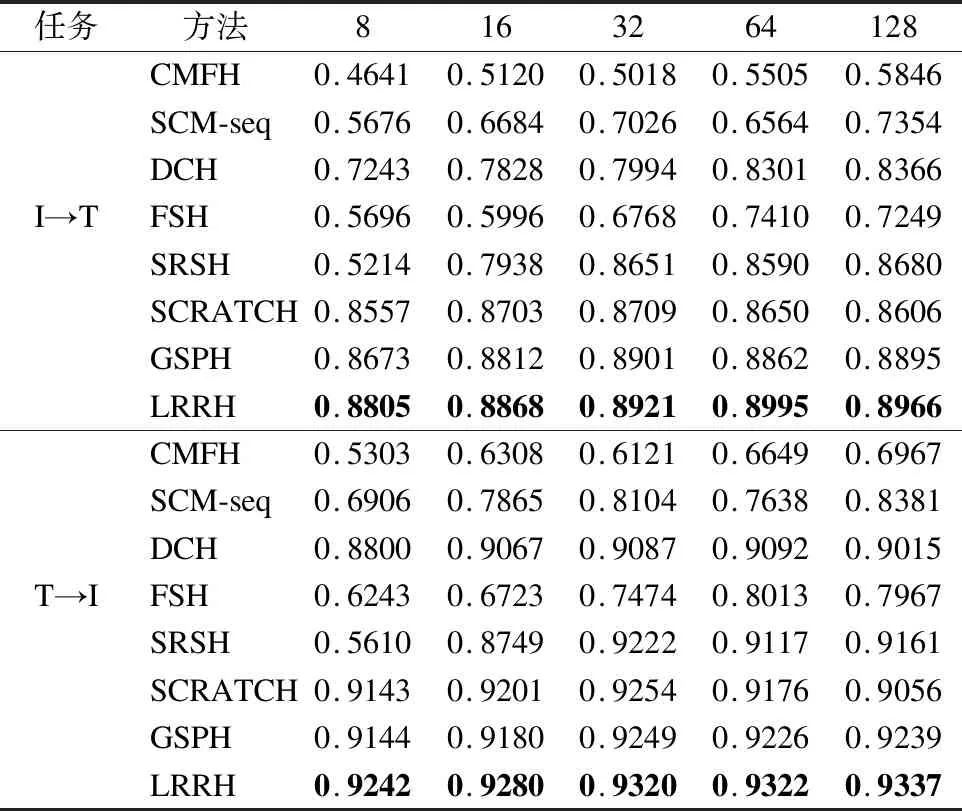
表3 在LabelMe上的MAP结果Table 3 MAP results on LabelMe dataset

从表3中可以发现，与所有对比方法相比，LRRH在所有的哈希码长度上都获得最佳的MAP结果，尤其是在文本检索图像的任务中，在所有哈希码位上MAP值都超过92%，同时，与SRSH相比，在I→T的任务中，MAP至少提高了2%，但是与对比方法中的最好结果相比，即GSPH，本文的LRRH性能提升并不明显，同时，从图2的 PR曲线可以看出，LRRH的曲线与部分对比方法非常接近，可能的原因是LabelMe是单标签数据集，在一定程度上限制了LRRH的学习能力.

从表3还可以看出，有监督的方法比无监督的方法表现更好，这也说明了语义信息的重要性.而大多数方法随着哈希码长度的增加会表现得更好，这表明更长的哈希码可以编码更多的判别信息，从而提高检索性能.

4.2.2 MIRFlickr数据集的实验结果

表4总结了MIRFlickr数据集上所有方法的MAP结果，图3分别展示了在16位和64位哈希码长度下的PR曲线.

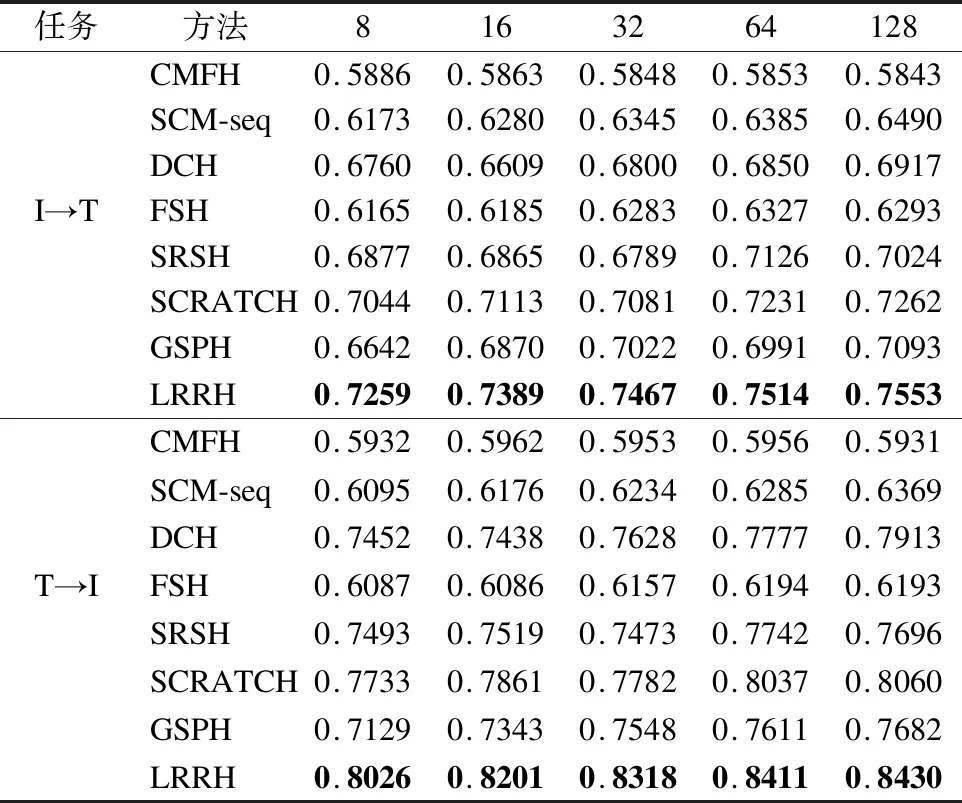
表4 在MIRFlickr上的MAP结果Table 4 MAP results on MIRFlickr dataset

从表4可以看出，在该数据集下，LRRH的MAP结果要优于其它所有对比方法.与SRSH相比，LRRH的性能提升显著.同时，与对比方法中表现最好的SCRATCH相比，在I→T的任务中，LRRH最好结果大约高出了3.8%；而在T→I的任务中，最好结果大约高出了5%.从图3的PR曲线可以看出，LRRH总体表现也优于其它对比方法，且在文本检索图像任务中有较大的优势.与LabelMe数据集不同的是，MIRFlickr是多标签数据集，且类别数也较多.该数据集的实验结果表明了LRRH考虑到了标签的类别信息，而此类信息对于检索效果也很重要，因此在类别数较多的多标签数据集上，LRRH更能体现其优越性.

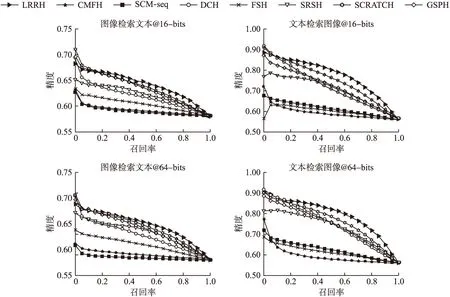
图3 在MIRFlickr上哈希码分别为16位和64位时的PR曲线Fig.3 PR curves on MIRFlickr with the code length of 16 bits and 64 bits

4.2.3 NUS-WIDE数据集的实验结果

表5显示了在NUS-WIDE数据集上的MAP结果，而图4分别绘制了在16位和64位不同哈希码长度下的PR曲线.

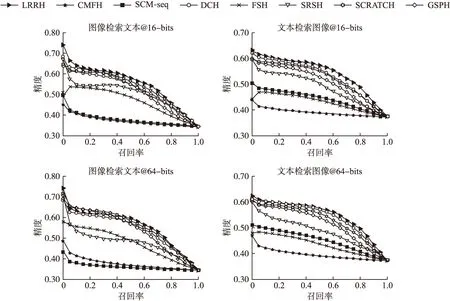
图4 在NUS-WIDE上哈希码分别为16位和64位时的PR曲线Fig.4 PR curves on NUS-WIDE with the code length of 16 bits and 64 bits

从表5可以得出与前两个数据集相同的观察结果是：LRRH在所有情况下，MAP结果始终优于所有对比方法，这也很好说明了本文提出的LRRH在跨模态检索中的有效性.与SRSH相比，LRRH性能提升更为显著.在图4的PR曲线中，总的来说，LRRH表现也优于其它对比方法.这说明了LRRH能更充分地利用标签的语义信息，具有更强的语义判别能力，对多标签数据集有更好的学习能力.

表5 在NUS-WIDE上的MAP结果Table 5 MAP results on NUS-WIDE dataset

4.2.4 收敛分析

在本节中，本文进行实验以验证迭代优化算法的收敛性.图5展示了LRRH在3个数据集上哈希码长度分别为32位和64位时的收敛曲线.可以看出，作为优化算法的结果，本文的目标函数在不同的3个数据集上仅仅需要3次迭代就能收敛.同时，无论是在LabelMe的小规模数据集上还是在NUS-WIDE之类的大规模数据集上，优化算法收敛都非常快，这表明本文优化算法具有一定的优势.而为了取得最优的结果，本文对不同的数据集统一将迭代次数设置为3次.

图5 迭代优化算法的收敛性分析Fig.5 Convergence analysis of iterrative optimization algorithm

4.2.5 参数敏感性分析

本小节在LabelMe数据集上进行实验分析了参数γ，η，λ1和β的变化对MAP结果的影响.其中，λ2=1-λ1，哈希码长度设置为16位，在测试每个参数的同时保持其他参数不变，被固定的其他参数采用4.1节实验设置中LabelMe上的参数取值.图6显示了各参数的变化对MAP结果的影响.其中，参数γ控制标签松弛回归项在方法中的影响程度，参数η控制量化误差项在方法中的影响程度，参数λ1控制图像模态的权重，参数β控制正则化项的惩罚程度.从图6可以观察到，当参数γ的值从1增加到100时，在图像检索文本的任务上，效果有不小的提升，表明标签松弛回归项对哈希码质量的提升是有效的.而参数η在[0.01，0.1]范围内，对结果影响较大，说明量化误差项对LRRH的性能也有一定的贡献.参数λ1的值取在0.3附近时，表现的结果较好，说明在LabelMe上，应适当侧重文本模态.正则化参数β的值取在0.001附近时，结果表现最佳，当它取值太大时，结果显著下降，因为此时导致模型欠拟合，而取值太小时，会使得模型容易过拟合.同时也可以发现，本文方法在各参数的较大范围内都能表现良好.

图6 LabelMe数据集上参数γ，η，λ1，β的敏感性分析Fig.6 Sensitivity analysis of parameters γ，η，λ1，β on LabelMe dataset

4.2.6 训练时间对比分析

在本小节中，进行了实验，对比所有方法在3个数据集上哈希码长度分别为32位和128位时的训练时间，其结果总结在表6中.从表6可以看出，大部分方法在哈希码长度为128位时的训练时间要比32位时增加不少，而LRRH的训练时间并没有明显增加，主要原因是LRRH是同时生成哈希码的所有位而不是逐位生成.在NUS-WIDE大型数据集上，部分方法训练时间将近1000秒，其中SRSH则超过了5000秒，尽管LRRH使用了n×n的相似度矩阵从而计算复杂度无法与训练集大小成线性关系，但因为本文优化算法的有效性和稳定性，使得迭代次数较小，所以在NUS-WID大型数据集上，LRRH训练时间并无很高.

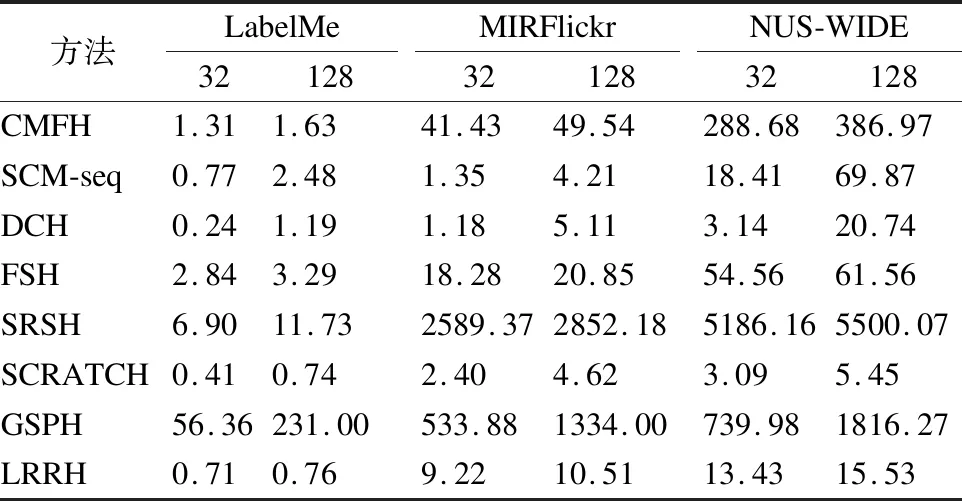
表6 3个数据集上所有方法的训练时间(单位：秒)Table 6 Training time(second)of all methods on three datasets

5 总结与展望

本文提出了一种新的有监督跨模态哈希方法，即标签松弛回归哈希，简称LRRH.LRRH通过引入语义相似度矩阵来保持实例间的语义相似性，同时为了也保留标签的类别信息，LRRH将标签矩阵扩展为标签松弛变量矩阵，通过标签松弛回归将标签的类别信息嵌入到哈希码中，同时添加正交与均衡约束，使学习到的哈希码判别力更强.此外，在哈希码的求解中，能离散地一步生成哈希码的所有位.在3个公开数据集上与最近的跨模态哈希方法进行了实验比较，实验结果表明，在跨模态检索任务上，LRRH优于最近的一些方法，具有较好的优越性.

下一步工作将考虑引入子空间学习，使其和哈希码之间建立关联，加强哈希码之间的语义相关性，同时也将进一步考虑不同模态特征表示间的语义层上的相关性.