面向密文数据的OPTICS聚类模型

栗维勋，马 斌，王 琛，何纪成，高明慧，徐 剑

1(国网河北省电力有限公司，石家庄 050000)

2(南瑞集团有限公司(国网电力科学研究院)，南京 210061)

3(北京科东电力控制系统有限责任公司，北京 100192)

4(东北大学 软件学院，沈阳 110169)

E-mail：1193328465@qq.com

1 引 言

聚类作为典型的数据分析与挖掘技术，在众多领域发挥着重要作用[1-3].聚类属于机器学习中的无监督学习，目的是把数据点划分成若干类，同一个类中的数据点有很大的相似性，而不同类的数据点有很大的相异性.聚类可以在大量数据中获取有用的知识，找出数据之间的潜在关系，是智能推荐、信息检索、图像模式识别、网络实时监控和预警等领域中的常用技术手段[4-6].

随着云计算、物联网以及5G技术的飞速发展，催生大数据时代快速到来.但是，在实际应用场景中，部分数据拥有者由于资源受限，需要将数据进行外包.因此，外包聚类服务也随之产生，成为聚类方法发展的新趋势[7-9].数据外包后，如何保障其隐私性是一个具有挑战性的问题.外包的数据常常包括金融、生物医学等个人敏感信息，一旦发生数据泄露问题，对个人或社会将产生严重的负面影响[10].针对上述问题，目前，通常的做法是对外包的数据进行加密处理.然而，传统的聚类方法仅能对明文数据进行聚类，不支持密文数据的聚类.因此，研究密文数据上的聚类方法就变的重要而迫切.

在密文数据上实现聚类是当前隐私保护机器学习研究的热点问题之一[11-13].目前，众多学者采用同态加密来支持密文数据上的运算[13，14-17].Cheon等人[13]实现了密文上的均值漂移算法，将非多项式内核替换为多项式内核，以便可以在同态加密下高效的计算，降低了传统均值漂移算法的超线性复杂度，在速度和准确性方面有了提升.Almutairi等人[14]利用同态加密技术设计了一种可更新距离矩阵，利用矩阵计算的性质来对密文进行计算.Hyeong等人[15]提出了支持比较操作的安全协议，首先使用Paillier密码系统对明文数据进行加密，然后将明文运算操作替换成密文安全协议.虽然使用Paillier算法可以保证语义安全性，但是计算消耗较高.Chen等人[16]设计了一种基于Paillier加密的智能电表数据聚合方案，保护用户的隐私信息.该方案引入可信的第三方密钥生成中心，为用户生成合法的密钥，用户密钥保存在服务器中用于验证用户的合法身份.Angela等人[17]则解决了密文运算中的除法问题，同态加密中不允许两个密文数据直接相除，但可以用一个密文数据除以常数，这个常数代表数据总和，即使暴露也不会泄露关键信息.Xing等人[18]提出了一种基于同态加密的K-means聚类方案，该方案既不会泄露个人信息，也不会泄漏社区的特征数据.在该方案中，聚类的每次迭代调用的隐私保护算法，可在不泄漏每个参与者标签的情况下计算簇类中心.参与者无法获知同一簇类中的其他参与者信息.通过安全性分析，即使存在共谋参与者，也不会泄露其余参与者的私人信息.Almutairi等人[19]考虑到现有方法都需要所有数据拥有者参与，参与的数据量过于庞大，客户端计算能力不足，因此引入可信第三方，将计算外包给第三方，节约计算成本，同时保证相互之间的隐私性.

综上所述，在密文聚类方面，学者们已经提出了较多的研究方案.但是，仍存在如下问题：

1)多数密文上的聚类方案都是利用同态加密算法结合K-means算法实现，基于密度聚类的算法较少.而K-means算法存在需要预先输入聚类簇数以及对初始聚类中心过于依赖等缺点，无法满足某些场景的实际应用需求，因此还需在密文上实现其他聚类算法.

2)已有方案很多采用同态加密算法，该算法仅能支持加法或者乘法运算，而全同态加密可同时支持密文下的加法和乘法运算，构建的通信协议也更加简单.

因此，本文利用全同态加密技术研究面向密文数据的密度聚类模型，并将密度聚类的典型代表OPTICS算法作为研究切入点.首先，设计了面向密文数据的OPTICS聚类模型(OPTICS-CMED)，对OPTICS-CMED的实体构成和形式化定义进行了描述；设计了对应于基本操作的通信协议，包括：距离计算协议和排序协议.基于上述通信协议，构建OPTICS-CMED的聚类过程.对OPTICS-CMED的正确性、安全性进行了分析，结果表明该模型可以同时保证正确性和安全性.最后，利用标准实验数据进行性能测试，结果表明该模型可以在保证聚类准确性的前提下实现密文数据聚类.

2 OPTICS概述

OPTICS是一种无需用户提供特定密度阈值的密度聚类算法，是DBSCAN(Density-Based Spatial Clustering of Applications with Noise)的改进算法，其不明显的产生类簇，而是通过对结果队列中的样本点进行排序，来表达数据的基于密度的聚类结构[20].由于OPTICS算法输出的是一个排好顺序的样本点队列，称为结果队列，相较于DBSCAN，OPTICS算法对输入的参数不敏感.

OPTICS算法的核心思想：对于簇Ci中任意对象p，在其ε邻域Nε(p)中，至少存在MinPts-1个其他对象，其中ε代表欧氏距离半径，MinPts表示使得对象p作为核心对象在它的ε邻域中至少应含有的对象数量.

OPTICS算法中，存在核心距离core-distance(cd)和可达距离reachability-distance(rd)两个概念.

定义1.对象p的核心距离cdε，MinPts(p).设半径参数为ε′，使得p的ε′邻域刚好包含MinPts个对象，若p不是关于ε′和MinPts的核心对象，则p的核心距离没有定义，如式(1)所示：

(1)

定义2.对象p到对象q的可达距离rdε，MinPts(p，q).是使p从q密度可达的最小半径值，其中q必须是核心对象，并且p必须在q的领域内，如式(2)所示：

rdε，MinPts(p，q)=

(2)

OPTICS聚类算法，最终将根据识别结果输出数据集的簇排序，该排序给出了对数据结构化和聚类的一般观察.

3 模型构建

3.1 模型描述

OPTICS-CMED包括两方实体，即客户(Client，C)和服务器(Server，S)，如图1所示.

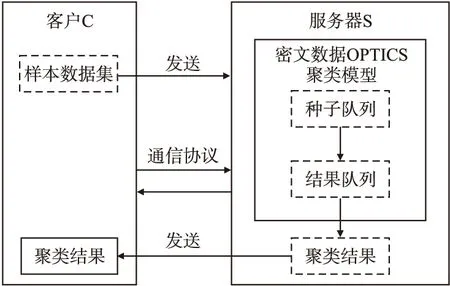
图1 面向密文数据的OPTICS聚类模型Fig.1 OPTICS clustering model over encrypted data

在OPTICS-CMED模型中，聚类过程由S与C通过安全通信协议交互完成.C将加密的样本数据集发送给S，S进行聚类，并生成种子队列和结果队列，其中结果队列包含着表示聚类结构的簇排序对象列表，从结果队列中可以得到聚类结果.整个过程在密文下进行，在计算样本点与中心点的距离时不会泄露隐私，通过隐藏类簇中心来防止攻击者推断出用户所属的类簇分组.在图1中虚线区域表示需要保护隐私的数据及模型，其中聚类模型仅能被S获知，而明文聚类结果仅能被C获知.

定义3是对OPTICS-CMED的描述.

定义3.密文数据的OPTICS聚类模型(OPTICS-CMED)可以由如下元组表示{C，S，Distance，getOrder}.

1)Distance(E(x)，E(y))：安全距离计算协议，将FHE加密的数据E(x)，E(y)作为参数输入，得到加密向量的乘法平方结果，即欧几里德距离结果，保存到数组中；

2)getOrder(E(rd0)，…，E(rdm-1))：排序协议，将FHE加密的可达距离数组rd作为参数输入，完成密文下可达距离的排序.

3.2 通信协议

OPTICS-CMED的通信协议包括安全距离计算协议和排序协议.安全距离计算协议用于实现两个加密的向量的欧氏距离计算；排序协议用于实现对多个加密数据进行从小到大排序.

3.2.1 安全距离计算协议

安全距离计算协议是利用FHE的加法同态和乘法同态性质，计算由FHE加密的两个向量的欧氏距离的平方，返回一个FHE加密的运算结果.在安全距离计算协议中，S的输入是两个加密的向量数据和用于加密的密钥，距离计算仅由S即可完成.S获得FHE加密的向量点乘结果用于后续计算核心距离和可达距离，同时保证数据的隐私.

协议1是安全距离计算协议的描述.

协议1.安全距离计算协议distance(E(x)，E(y))

S：E(x)=(E(x1)，…，E(xd))，E(y)=(E(y1)，…，E(yd))，pk；

S：E(s)

1.S：Ef(s)←Ef(0)

2.S：for1≤i≤d：

3.S：E(zi)←(E(xi)⊙E(yi))×(E(xi)⊙E(yi))

4.S：E(s)←E(s)⊕E(zi)

5.S：returnE(s)

3.2.2 排序协议

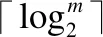
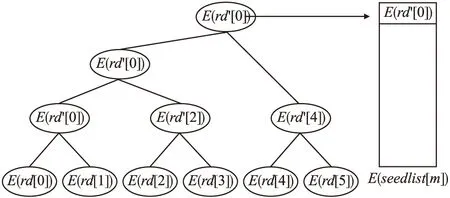
图2 排序过程Fig.2 Process diagram of ordering

在排序过程中，找到数组中最小值，将它与数组的第1个元素交换位置；再在剩下的元素中找到最小值，与数组的第2个元素交换位置.循环下去，直到完成对整个数组的排序.而获取最小值的方法：利用两个元素的比较协议，对数组中的元素进行两两比较，找到数值较小的一方赋值给下标小的一方，放入另一个数组中；同时使下标较大的一方数值为0，直到所有比较完成.再对另一个数组中的元素进行两两比较，重复上述过程，最后得到一个最小值.

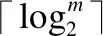
协议2是对排序协议的具体描述.

协议2.排序协议getOrder(E(rd[0])，…，E(rd[m-1]))

输入S：E(rd[0])，…，E(rd[m-1])，公钥pk；

输入C：私钥sk；

输出S：有序数组E(Qorder[k])

1.S：for0≤k≤m

2.S：for0≤i≤m：

3.S：E(rd′[i])←E(rd[i])

4.S：num←m

6.S：for1≤j≤⎣num/2」

7.C，S：flag=Compare(E(rd′[2i(j-1)])，E(rd′[2i(j-1)+2i-1]))

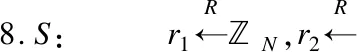
9.S：E(rd1)←E(rd′[2i(j-1)])⊕E(r1)

10.S：E(rd2)←E(rd′[2i(j-1)+2i-1])⊕E(r2)

11.S： sendE(rd1)E(rd2)toC

12.C：if(flag==1)

13.C：E(rdmin)←E(rd1)

14.C：else：

15.C：E(rdmin)←E(rd2)

16.C： sendE(rdmin) andE(flag)toS

17.S：E(rd′[2i(j-1)])←E(rdmin)⊕(E(flag)⊙E(1))⊗r2⊙E(flag)⊗r1

18.S：E(rd′[2i(j-1)+2i-1])←E(0)

19.S：num←「num/2⎤

20.S：E(rdmin)←E(rd′[0])

21.S：E(Qorder[k])←E(rdmin)

3.3 聚类过程

在OPTICS-CMED模型的聚类过程中，S将半径ε和最小点数MinPts两个参数作为输入，计算每个元素的核心距离(cd)和可达距离(rd)，完成后续聚类过程.

OPTICS-CMED的聚类过程如下：

Step 1.C对数据进行处理，将浮点数转化成整型，对数据进行加密，发送待聚类数据集x、半径ε和最小点数MinPts给S，并向S提交聚类服务请求；

Step 2.S收到C的聚类服务请求后，开始进行聚类，创建两个队列，种子队列Qorder和结果队列Qreachdist；

Step 3.如果x中的数据全部处理完，则算法结束；否则，从x中选择一个未被处理的核心对象，找出它的所有直接密度可达点，如果该点不存在于Qreachdist中，则将其存入Qorder中，并调用getOrder协议，与C共同完成可达距离rd排序；

Step 4.如果Qorder为空，则执行Step 3；否则，从Qorder中取出第一个样本点：

Step 4.1.判断该点是否为核心对象，如果不是，则跳至Step 4；否则将该点存入Qreachdist；

Step 4.2.若该点是核心对象，找到它的所有直接密度可达点，存入Qorder，并调用getOrder协议，将Qorder的点按照rd重新排序.如果该点已经在Qorder中且新的rd较小，则更新该点的rd；

Step 4.3.若Qorder中不存在直接密度可达样本点，插入Qorder中，调用getOrder协议，将Qorder的点按照rd重新排序；

Step 5.输出Qreachdist中的有序样本点，发送给C；

Step 6.C进行解密得到明文聚类结果.

4 正确性与安全性分析

4.1 正确性分析

首先对安全距离计算协议和排序协议进行分析，并进而证明OPTICS-CMED的正确性.

1)安全距离计算协议

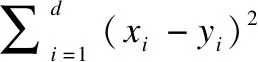
综上所述，本文的安全距离计算协议是正确的.

2)排序协议

排序协议中主要采用了选择排序的思想，在未排序序列中找到最小值放在序列起始位置；在剩余的数据中继续排序找出最小值，将其放在已排序序列的队尾；重复上述过程直到处理完所有数据.

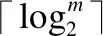
在求最小值协议中，通过调用加密数据的比较协议Compare()实现两个密文数据的比较，由C得到比较结果flag.然后，S将两个增加随机值的待比较的数据d1，d2发送给C，其中d1=dl+r1，d2=dr+r2，r1，r2，是随机数，dl表示左值，dr表示右值.

当flag=1时，dmin←d1；

当flag=0时，dmin←d2.

保证dmin记录的是最小值.C将dmin和flag一同发送给S，S根据dmin=dmin+(flag-1)×r2-flag×r1去除干扰值得到真实的最小值dmin.

当flag=1时，dmin=d1=dleft+r1，则：

dmin=dleft+r1+(1-1)×r2-1×r1=dleft；

当flag=0时，dmin=d1=dright+r2，则：

dmin=dright+r2+(0-1)×r2-0×r1=dright.

因此，S可以成功去除干扰值获得明文最小值dmin，并用下标较小的数组存储最小值，同时将下标较大数组置0，最后d0存储m个元素中的最小值.

综上所述，本文的排序协议是正确的.

3)OPTICS-CMED

在OPTICS-CMED中，首先调用比较协议判断当前加密的样本数据点是否是核心对象，再利用一个辅助数组vi来判断该数据点是否被访问过.由于在密文下无法得知vi的值，需要C的帮助，为防止数据泄露，S对其增加干扰值后发送给C进行解密，最后S再去除干扰值得到真正的vi值.若vi=0表示当前数据点未被访问过，vi=1表示当前数据点已经被访问过.再调用排序协议对可达距离进行排序，保证最后可以得到有序的数组E(Qreachdist[d]).由于安全距离计算协议和排序协议都是正确的，得到包含聚类结果的E(Qreachdist[d])逻辑上也是正确的.

综述所述，OPTICS-CMED也是正确的.

4.2 安全性分析

本节在半诚实模型下对通信协议和OPTICS-CMED的安全性进行分析，C和S都是半诚实的参与方，它们诚实地遵循协议的执行，允许从协议执行过程中获取的数据进行推断.其输入数据是隐私数据，仅能被个人获知.

1)安全距离计算协议

在安全距离计算协议中，S的视图为VS=(E(yi)，E(xi)，E(zi)，E(s)).由于FHE是语义安全的，S无法从E(xi)，E(yi)，E(zi)和E(s)中提取出明文xi，yi，zi，s，保证了数据xi，yi，zi，s的隐私；此协议仅由S执行，C无法获得隐私信息.

因此，本文设计的安全距离计算协议在半诚实模型下是安全的.

2)排序协议

在排序协议中，S的视图为VS=(E(rd[m])，pk，r1，r2，E(rdmin)，E(Qorder[k]))，其中r1，r2是随机数.C和S首先调用加密数据的比较协议对S的加密数据E(rd[m])进行比较，C获得明文的比较结果flag，由于加密数据的比较协议的安全性，保证了C和S比较过程中数据的隐私.接着，S将增加随机干扰的密文数据E(rd1)和E(rd2)发送给C，C根据比较结果flag，将密文E(rd1)和E(rd2)赋值为E(rdmin)，再返回给S.由于FHE加密算法是语义安全的，C即使对密文数据E(rdmin)与EP(rd[m])解密也无法获取明文rdmin和rd[m].由于比较结果仅被C获知，C将更新后的密文发送给S，因此S无法通过密文E(rdmin)，E(rd[m])，获知左值和右值哪个是最小值，保证了待比较数据在S方的隐私.C的视图为VC=(skP，flag，E(rd1)，E(rd2))，由于E(rd1)，E(rd2)是增加随机干扰值的密文数据，即使C可以使用私钥解密也很难从明文rd1和rd2中提取出真实值，从而保证了待比较数据在C方的隐私.虽然C能够获知比较结果，但其无法获知待比较数据的真实值，无法进行推断.因此，本文的排序协议在半诚实模型下是安全的.

综上所述，本文所设计的通信协议在半诚实模型下都是安全的.

3)OPTICS-CMED

在OPTICS-CMED中，首先，调用比较协议用于判定该加密数据点是否为核心对象.比较协议在半诚实模型下是安全的，S将增加噪声干扰的最高位发送给C，保证其解密后无法得到最高位的明文，从而不知道数据的大小.S不拥有FHE私钥，无法解密，因此比较过程是安全的.

通过调用安全距离计算协议计算两个加密数据点的欧氏距离的平方，即核心距离.安全距离计算协议在半诚实模型下是安全的，整个过程仅在S方进行，未向C方发送任何数据，保证了S方加密数据的安全性.S方不拥有私钥，无法解密待计算的数据，又因为FHE的加法与乘法同态性，保证计算过程的安全性，因此安全距离计算时是安全的.

最后，先调用更新数组函数将未访问的数据点放入种子数组中，再调用排序协议获取有序数组，由于S对数组下标填加干扰值，即使C拥有解密的私钥也无法获知真正的下标顺序.协议2在半诚实模型下是安全的，得到的数据也是安全的，C无法得知密文的最小值，无法获取待比较数据的大小关系，保证了数组元素的大小关系不会泄露给C.

综上所述，基于安全距离计算协议与排序协议进行构造的OPTICS-CMED在半诚实模型下也是安全的.

5 实验分析

本文的实验环境如表1所示.加密方案中的密钥长度为1024位，安全参数λ=100.由于FHE方案仅能对整数进行操作，本节使用IEEE 754双精度浮点数代表实数，精度为52位，然后通过乘以大的实数来进行变换.

表1 实验环境Table 1 Test environment

实验采用4种FCPS标准数据集(1)http：//uni-marburg.de/fb12/datenbionik/data?language svnc=1/，分别为：Hepta、Lsun、Tetra、Wingnut公共数据集.OPTICS聚类的性能主要由参数ε与MinPts决定，为了获得最优的聚类效果，对参数ε与MinPts的不同取值情况下的OPTICS聚类性能进行测试，采用轮廓系数来评价聚类效果.利用4种数据集，对OPTICS-CMED与明文下的OPTICS进行对比，参数与轮廓系数关系如图3-图6所示.参数ε越小，明文OPTICS聚类算法与OPTICS-CMED的轮廓系数均越来越大，说明聚类效果得到提升.

由图3和图4对比可知，MinPts值越大，轮廓系数越小，表示其聚类性能有所下降.当参数ε小到超过数据阈值时，将无法完成聚类.

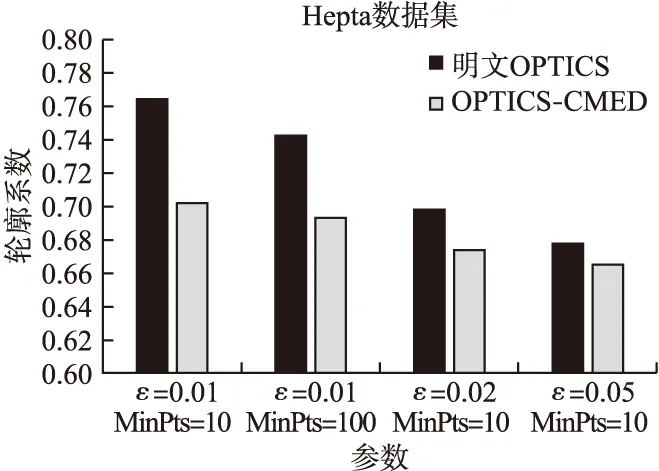
图3 参数与轮廓系数关系(Hepta数据集)Fig.3 Relationship between parameters and silhouette coefficient(Hepta dataset)

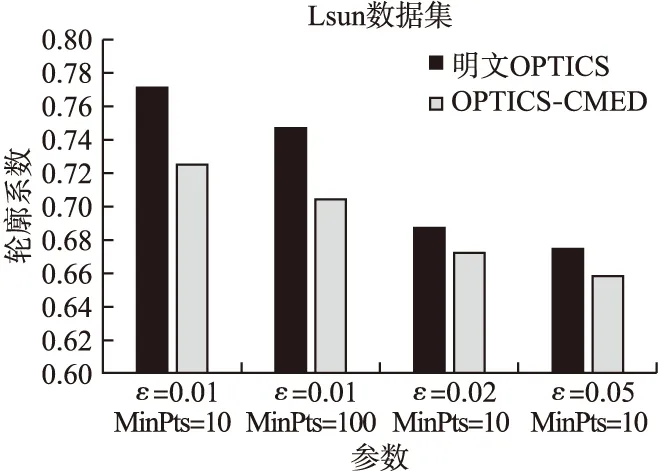
图4 参数与轮廓系数关系(Lsun数据集)Fig.4 Relationship between parameters and silhouette coefficient(Lsun dataset)

从图4～图6中数据分析可知，OPTICS-CMED聚类轮廓系数比明文OPTICS算法低1.3%～8.1%，且轮廓系数均超过0.6，在可接受范围内，因此OPTICS-CMED可以在密文下完成聚类，且聚类效果可以得到有效保障.

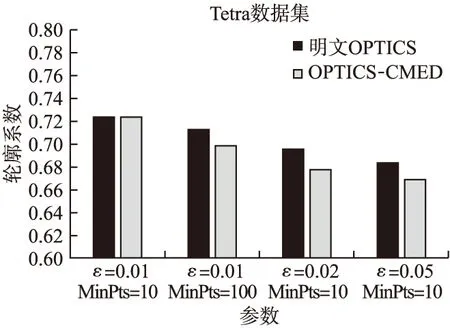
图5 参数与轮廓系数关系(Tetra数据集)Fig.5 Relationship between parameters and silhouette coefficient(Tetra dataset)

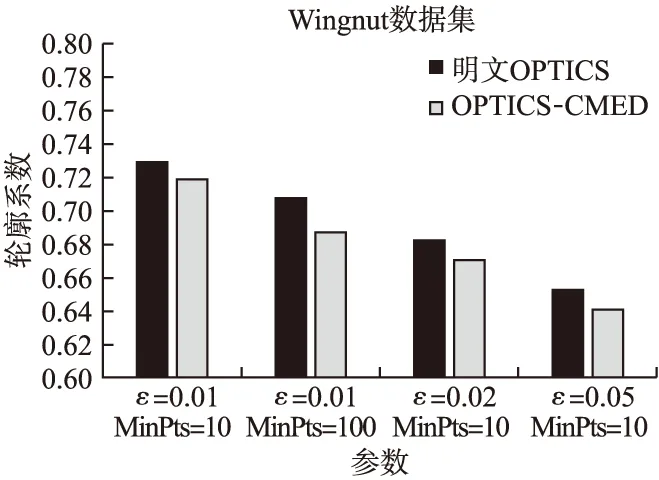
图6 参数与轮廓系数关系(Wingnut数据集)Fig.6 Relationship between parameters and silhouette coefficient(Wingnut dataset)

采用F1-score对本方案进行实验分析.在聚类中，精确率(Precision)和召回率(Recall)是相互矛盾的，F1-score会同时考虑精确率和召回率，重新计算新的分数，如式(3)所示，当F1-score较高时则能说明实验方法有效.

(3)

表2给出了参数ε与MinPts的不同取值情况下的OPTICS-CMED与明文OPTICS对比结果.

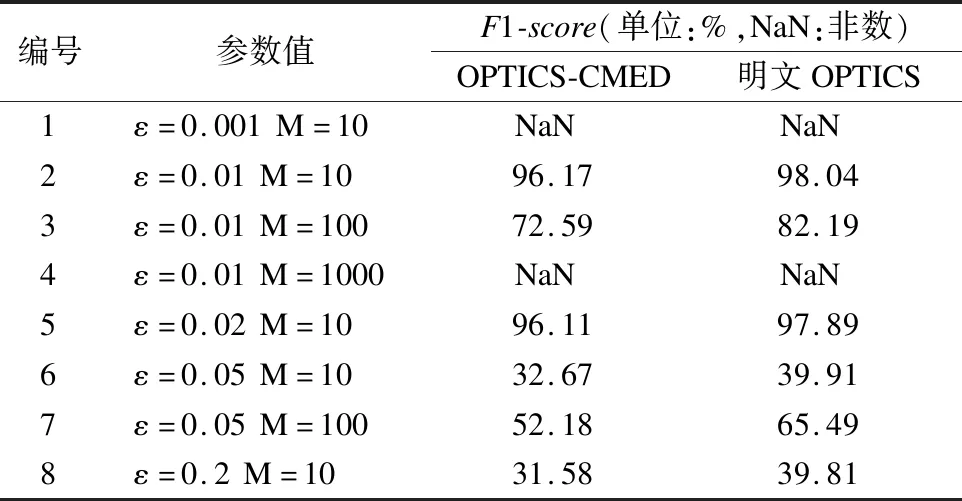
表2 OPTICS-CMED与明文OPTICS的F1-score对比结果Table 2 F1-score comparison of OPTICS-CMED and plaintext clustering

表2中1与2、5与6对照数据可知，当MinPts相同时，参数ε越小，F1-score越来越大，整体性能得到提升；但当参数ε达到最低阈值时，将无法聚类.由2与4、6与7组对比数据可知，MinPts值越大，F1-score也越来越大.

综合分析轮廓系数与F1-score可知，当OPTICS参数ε=0.01且MinPts=10时，聚类效果最优.

在参数为ε=0.01且MinPts=10情况下，利用Lsun数据集(n表示数据总数，取n=50、100、200、300、400)分别进行实验.

表3给出了当n变化时明文聚类与OPTICS-CMED模型客户端和服务器运行时间的对比.数据表明，其运行时间随n线性增长，服务器承担了主要的开销，减轻了客户端的负担.

表3 明文聚类与OPTICS-CMED的时间开销对比Table 3 Time cost comparison of plaintext clutering and OPTICS-CMED

6 结束语

针对面向密文数据的OPTICS聚类研究成果较少的问题，利用全同态加密构建了面向密文数据的OPTICS聚类模型(OPTICS-CMED).首先，对OPTICS-CMED的实体构成进行介绍，给出了形式化定义，详细描述了模型的通信协议及其在聚类过程中的调用方式，从正确性、安全性两方面进行理论分析，通过实验对模型进行性能测试，结果表明本文设计的OPTICS-CMED能够在密文下完成聚类运算，同时可以保证在密文下的聚类效果，具有一定的实际应用价值.