基于VMD能量熵及LSSVM的减速顶故障检测方法
2022-10-15穆鹏丞金志浩
穆鹏丞, 金志浩
(沈阳化工大学 装备可靠性研究所, 辽宁 沈阳 110142)
在铁路货运系统中,由于各车厢的目的地不同,列车需要在编组站进行解体并重新编组.列车编组站对列车的编组形式以驼峰编组为主[1].在编组时,为防止列车自由溜向某一轨道发生冲撞,需要使用减速顶进行调速.减速顶是通过滑动油缸帽头与车轮接触时产生的反作用力对车厢起到制动、调速作用的设备,被广泛应用于各种铁路编组站[2].减速顶的工作状态严重影响列车在溜车时的位置以及安全连挂,所以,监测减速顶的健康状态在驼峰编组工作中是极其重要的.
减速顶的故障类型主要表现为滑动油缸组合件破损失效.现阶段对减速顶的故障检测手段主要依赖于人力巡检,通过采用脚踩的方式凭借人工经验来判断减速顶的工作状态[3].现阶段,由于信息技术和工业技术的发展,一些其他检测手段在铁路系统中得到了应用,如室外实车检测、室内模拟检测以及减速顶油气压力检测仪[4-5].但这些技术都存在一定的局限性,如:室外实车检测方法成本高、效率低;室内模拟实验台检测方法的故障识别率不高、检测周期长、且不能同时检测多个减速顶;减速顶油气压力检测仪的检测成本过高、费时费力[6].
声发射技术是一种新型无损检测技术,由于其采集的信号是机械结构所产生的高频应力波信号,具有不易受振动以及环境噪声的干扰等特点,因此被广泛应用于机械设备工作状况的检测.李晓晖等[7]利用声发射信号有效实现了机械密封端面健康情况的无损检测,证明了声发射技术在无损检测领域的前景;党轩等[8]将声发射传感器布置在柴油机表面的不同位置,通过对比不同测点的异常声发射信号峰值响应来定位故障源.
变分模态分解(variational modal decomposition,VMD)是一种完全非递归、且具有完备数学理论支撑的信号处理方法[9].相比于小波变换,VMD克服了小波阈值的不同选取对信号分解、降噪时的影响;相比于EMD分解,VMD避免了EMD分解时带来的模态混叠和端点效应,因此VMD非常适用于处理分析声发射信号[10].
针对铁路货运系统中不能实时检测减速顶状态,从而可能会造成列车冲撞、脱轨,影响铁路运输并造成重大经济损失的问题,根据声发射信号能体现机构内部破裂和变形的剧烈程度,且VMD能量熵可以较好体现机械零件的破损程度的优点,并考虑到减速顶的故障检测效率,本研究提出了一种利用声发射技术、VMD能量熵及最小二乘支持向量机(least squares support vector machine,LSSVM)的减速顶故障实时检测方法.该方法可以在极短的时间内识别待测减速顶的健康状态,并且可以有效避免由于减速顶故障的检测不及时对铁路系统造成的危害.首先,使用VMD方法对减速顶声发射信号进行处理得到多个本征模态函数(intrinsic mode function,IMF);然后,提取各IMF分量信号的能量熵作为LSSVM训练的特征向量;最后,用训练得到的模型对未知状态的减速顶工作状态进行识别.
1 变分模态分解
变分模态分解(VMD)是一种基于维纳滤波的完全非递归自适应信号处理手段[11].VMD可以将给定的复杂信号通过最优变分模型的频域迭代方式计算得到一系列分量信号的中心频率和带宽,进而获得一定数量调幅-调频的分量信号uk,k∈(1,2,…,K),其表达式为
uk=Ak(t){cos[φk(t)]}.
(1)
式中:Ak(t)是第K个IMF分量的振幅;φk(t)为相位.
在求解信号的中心频率和带宽的过程中,假设原多频带信号可分解为多个窄带IMF分量,需要建立如下约束变分模型表达式.
(2)
式中:ωk=φ′(t)是各uk(t)的中心频率;uk是第K个IMF分量;f是原始信号.
在该变分模型中,对uk(t)进行Hilbert变换得到单边谱,然后通过乘指数项e-jωt调节预估的中心频率,并将其频谱调整到相应的基带上.为了将原变分约束模型转换为非变分约束模型,引入增广Lagrange函数
(3)
式中:α是二次惩罚因子;λ是Lagrange因子.
最后利用交替方向乘子算法不断迭代求解出如下自适应中心频率及各IMF分量表达式.
(4)
(5)

VMD算法分解过程如下:
(1) 初始化uk、ωk、λ和N;
(2)N=N+1,进入算法的循环更新过程;
(3) Fork=1.k为假设分解的IMF的数量,由式(4)和式(5)更新uk及ωk;
(4) 由公式
(6)
更新λ;
(5) 重复步骤(3)和(4)直到满足迭代终止条件
(7)
2 最小二乘支持向量机
最小二乘支持向量机(LSSVM)是对支持向量机的拓展,LSSVM将传统SVM决策函数的不等式约束转化为等式约束,并采用二次损失函数作为最优化指标[12],这使得LSSVM在处理大数据的样本时具备更快的求解精度及运算速度,LSSVM的约束优化模型定义为:
(8)
式中:xi为输入信号序列;yi为输出信号序列;ω是权值向量;γ是二次惩罚因子;ξi是松弛因子;b是偏置向量.
根据Mercer定理,核函数定义为
K(xi,xj)=φ(xi)Tφ(xj).
(9)
为解决以上优化模型,引入拉格朗日函数及KTT条件,得到LSSVM模型为
(10)
式中αi为拉格朗日乘子.
LSSVM中的核函数选取径向基函数,如式(11)所示.
(11)
式中σ为核函数的宽度.
3 VMD能量熵
在列车由减速顶调速过程中,减速顶内部的缺陷会导致其产生不同于正常状态的应力波声发射信号.采集的声发射信号经过VMD分解为固定数量的本征模态信号时,此时表征减速顶状态的特征信息寄存于各IMF分量中.但由于IMF分量的带宽较窄,容易出现模态混叠,造成特征提取困难的问题.为了提高信号类型的识别效果,引入VMD信息熵的概念[13].
在VMD对不同状态的减速顶声发射信号f(t)进行分解时,可得到多个IMF分量信号,可由式(12)计算出不同IMF分量信号的能量E1,E2,…,Ek.
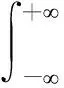
(12)
式中:ui为第i个IMF分量;t为采样时间.
由于VMD分解的IMF分量具有正交性,因此k个IMF的能量之和恒等于原始信号f(t)中的总能量
(13)
式中:E为信号f(t)的总能量;Ei为第i个IMF分量信号的能量.
由于各IMF分量包含原始信号中的不同频率成分,且包含的能量值不同,因此形成了相应声发射信号在频域空间不同的能量分布,其对应的VMD能量熵为
(14)
式中pi=Ei/E,即第i个IMF的能量占总能量的比值.
依据VMD的分解结果得到减速顶各状态的能量熵如表1所示.从表1中可以看出正常状态减速顶的VMD能量熵值明显大于故障状态减速顶的能量熵值.这是因为当减速顶发生故障时,在其相应的频域空间内会发生共振现象,在这种情况下能量便会集中汇聚到该频率空间内,降低了能量分布的不确定性,所以VMD能量熵值较小.由于故障状态的共振影响更大,造成了能量更加集中在某一频域带内,因此故障减速顶的能量熵值明显小于正常状态的减速顶.

表1 不同工作状态减速顶的VMD能量熵Table 1 VMD energy entropy of retarders in different working states
4 基于VMD能量熵及LSSVM的故障诊断模型
本研究的故障诊断模型是在减速顶声发射信号基础上,使用VMD能量熵和LSSVM 相结合的方法对减速顶状态进行故障检测,具体流程如图1所示.具体步骤为:

图1 故障诊断模型的流程Fig.1 Flow chart of the fault diagnosis model
(1) 通过声发射检测仪采集不同健康状态减速顶的声发射信号;
(2) 利用VMD能量熵方法获取不同状态下减速顶声发射信号中各个频带内的能量值,并构建特征向量T=[E1,E2,…,Ek];
(3) 由于各IMF的能量熵值复杂,因此将其进行归一化处理得到T′={[E1/E],[E2/E],…,[Ek/E]};
(4) 将构建的特征向量训练LSSVM分类器,用以识别未知状态的减速顶.
5 试验验证
5.1 减速顶声发射信号分析
本实验在沈阳裕国站进行,试验装置布置如图2所示.本次实验采集减速顶故障状态及正常状态的减速顶声发射信号.实验中的声发射仪为北京声华兴业公司的SDAEA声发射检测仪,传感器型号为SR150 A.实验参数设置如下:设采样频率为1250 kHz,采样点数为2000,采样时间为1.6 ms,门槛值为40 dB.火车速度约为10 km/h,试验时共测减速顶8个,其中故障减速顶和正常减速顶均为4个.

图2 试验装置布置Fig.2 Schematic of experimental equipment arrangement
将采集到的两类信号进行时频域分析,所有正常状态和故障状态的减速顶时频域信号有高度的相似性,图3为采集到的不同工作状态的时域信号及其频谱图.

图3 不同状态减速顶的时频域波形图Fig.3 Time-frequency waveforms of retarders in different states
从图3(a)和图3(b)中可以看出正常状态的减速顶与发生故障的减速顶时域信号存在着一定程度的区别,但不明显.然而,从图3(c)和图3(d)中可以看出正常状态声发射信号的波形比较平滑,且频率的最高振幅在520 kHz附近;而故障状态的减速顶声发射信号的最高幅值在580 kHz附近,且峰值变化杂乱.从频谱图可分辨出正常状态和故障状态两种类型的减速顶.推测频谱不同的原因是当列车处于制动状态时减速顶会起到对车厢整体的制动减速作用,并且此时故障和正常的减速顶内部滑动油缸帽头与缸体所产生的应力差别极大,因此在某一频带内产生的应力波不同,即在该带宽内所产生的能量不同.由于从减速顶时频域图上分析减速顶状态需要人为经验,难以在单一的时频域图上快速准确地实现对缺陷的有效识别,且不能在编组站中达到线上的快速辨别,因此需要对信号进行相关处理后进行快速辨别.
5.2 构造VMD能量熵
将不同状态的减速顶产生的声发射信号进行VMD分解,经过分解得到的各个IMF分量信号能够较好地剥离出原始声发射信号中的实际组分.通过大量试验后设定VMD中IMF的数量K=5、α=2000.为了节省篇幅,仅绘制了故障状态减速顶声发射信号的时域图,如图4所示.从图4中可看出:设定的IMF的数量理想且不存在模态混叠,表明减速顶声发射信号中包含着这些频率成分的信号.
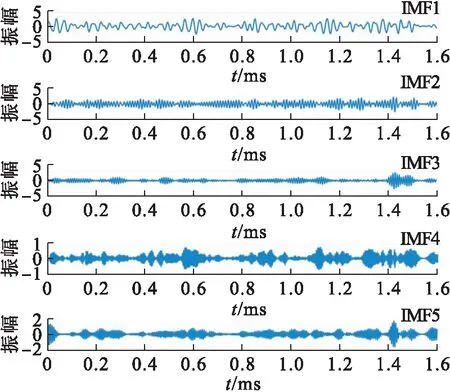
图4 VMD分解得到的故障减速顶声发射信号时域图Fig.4 Time domain diagram of acoustic emission signal of the fault retarder by VMD decomposition
为了实现在工程中达到对减速顶的快速、有效地检测,将VMD能量熵与LSSVM结合来实现减速顶的状态识别.在实验中,对正常和故障状态下的减速顶声发射信号分别采样,各得120组样本数据.首先将各组信号进行VMD分解得到IMF分量,再分别求取各IMF分量的能量熵后构建特征向量矩阵.由于篇幅原因,表2仅列出了每种状态下3组能量熵特征向量值.从表2中可以看出两种状态的能量熵值存在明显差异.此后将这些能量值作为训练LSSVM的输入特征向量.

表2 减速顶不同工作状态下的特征向量值Table 2 Eigenvalue vector of retarders in different working conditions
5.3 LSSVM的模式识别
随机选取两种状态各100组VMD能量熵值作为训练LSSVM的特征向量,其中LSSVM中的参数设置为惩罚因子γ=10、核函数σ=0.02.利用训练好的LSSVM识别两种状态共40组测试样本的状况,识别分类结果如图5所示.从图5中可看出仅有1个样本点识别错误.为了阐述VMD能量熵结合LSSVM的识别率及耗时方面的优越性,将其与目前常用的故障诊断方法进行了对比,如表3所示.从表3中可以看出:基于VMD能量熵结合LSSVM的减速顶声发射故障方法的识别率为97.5%,耗时为0.57 s.这种故障诊断方法在各方面皆优于被比方法,并且该方法在耗时及识别率上皆能满足编组站对减速顶状态实时监测工作的需求.
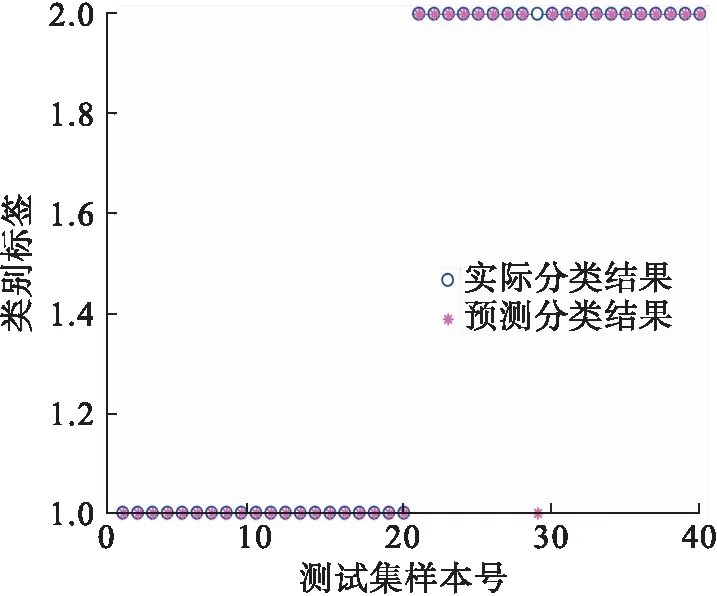
图5 LSSVM识别分类结果Fig.5 LSSVM recognition classification results

表3 不同诊断模型的识别率Table 3 Recognition rate of different diagnostic models
6 结 论
针对长期以来在列车编组站系统中需要人为经验判断火车减速顶工作状态的局限性,依据声发射信号能最大限度地反映减速顶内部破坏程度的优点,提出了结合VMD能量熵及LSSVM的减速顶故障诊断方法,得到了如下结论:
(1) VMD能够较好分解出减速顶声发射信号中的实际频率组分,且将VMD与能量熵结合后能够有效反映减速顶的损伤程度.
(2) 结合VMD能量熵及LSSVM的减速顶故障诊断方法能够在极短时间内完成对减速顶状态的识别,且识别率高达97.5%.这种故障检测方法能够满足列车编组站对减速顶故障实时监测的需求.
