二阶差商kNN在多模态过程故障检测中的应用

郭金玉， 刘玉超， 李 元

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

近年来，随着生产过程的复杂化与智能化，基于数据驱动的工业过程故障检测方法[1-6]备受国内外学者关注.主成分分析[7-11](principal component analysis,PCA)作为最早的统计过程控制算法，可以对数据进行降维，最大程度地保持了原有数据的信息.但是PCA是一种线性算法，在多模态非高斯分布的情况下，PCA方法得出的主元可能并不是最优的，此时在寻找主元时不能将方差作为衡量重要性的标准，具有一定的局限性.

为了克服PCA的局限性，提高工业生产过程的故障检测率，He等[12]提出基于k近邻(knearest neighbor,kNN)的工业过程故障检测方法，通过计算已知样本点到其k近邻样本的距离来实现故障检测，解决了工业过程的非线性和多模态问题.为了解决工业过程批处理数据的高维性和多条件性故障检测问题，Li等[13]提出一种局部保持测地线距离-k近邻(locality preserving geodesic distance-knearest neighbor,LPGD-kNN)方法，该方法通过对局部邻域(LNS)进行标准化处理，克服了多条件下预处理数据的特点，然后，利用局部保持投影方法提取多模态批次数据的自适应变换矩阵，形成新的建模数据.与传统的kNN方法不同，基于测地线距离的kNN方法提取相似信息，构造统计指标进行故障检测，准确表征局部区域内非线性数据的最短距离.为了检测非线性多模态工业过程中的故障，Zhong[14]等提出一种基于k近邻核独立分量分析的故障检测方法，该方法将过程数据与其k近邻进行标准化处理，消除多模态特性，考虑到数据变量之间的非线性相关性，利用核函数技术将原始非线性空间中的数据映射为线性空间，最后应用独立分量分析(independent component analysis,ICA)构造故障检测的监测统计量.但是，上述kNN及其扩展算法对于工业过程方差差异明显的多模态问题依然存在局限性.为了克服kNN的局限性，冯立伟[15]等将PCA与kNN相结合，并利用距离的权重对统计量进行加权，提出主元-加权kNN(PCA and weightedk-nearest neighbor，PC-WkNN)方法.与此同时，Guo[16]等分析了传统的kNN方法在密集模态下微弱故障的检测性能较差，提出一种基于概率密度kNN(kNN based on probability density，PD-kNN) 的多模态故障检测方法，该方法建立多个模型,实现多模态故障检测，不需要考虑模态间的不同方差差异，避免了小方差模态的微弱故障漏检的问题.为了建立单个模型提高传统kNN算法对方差差异明显的多模态过程监控性能，本文研究二阶差商kNN(kNN based on second order difference quotient，SODQ-kNN)在多模态过程故障检测中的应用，其主要思想是运用二阶差商算法对原始数据进行预处理，消除多模态和方差差异特性，在此基础上运用kNN进行故障检测.

1 基于二阶差商kNN的多模态过程故障检测方法

1.1 kNN算法

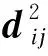
(1)

现用一个数值例子说明kNN算法的不足.随机生成一个方差差异较大的两个模态实例：模态1中，变量x1和x2为服从[0,0.05]的正态分布；模态2中，变量x1和x2为服从[3,1]的正态分布.每个模态分别产生100个正常样本,另外产生一个密集模态的故障样本.原始数据的散点图如图1所示.在kNN算法中，近邻数选2，利用kNN方法对该例子进行故障检测，其结果如图2所示.从图2可以看出:故障点在控制限下方，被模态2的样本覆盖.因此,利用近邻距离的平方和并不能将故障点与模态2的正常样本区分出来，kNN方法很难检测这类微弱故障.

图1 数据分布散点图Fig.1 Scatter plot of data distribution

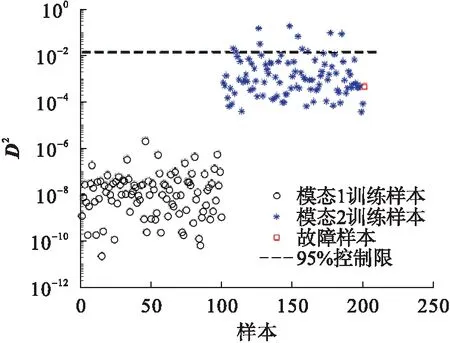
图2 kNN对训练与故障样本的检测结果Fig.2 Detection result of kNN for training and fault samples

1.2 二阶差商预处理算法

为了剔除数据的多模态特性，郭金玉等[17]提出运用差分(difference，DIF)算法对数据进行预处理，其计算方式为

(2)

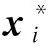
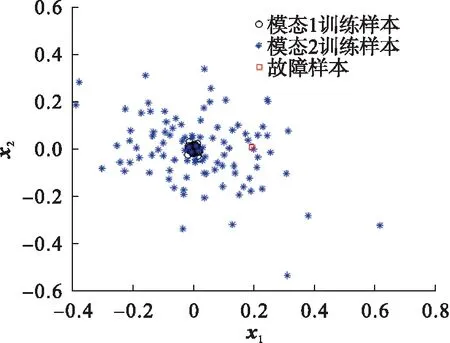
图3 DIF预处理的数据散点图Fig.3 Scatter plot of preprocessed data by DIF

为了克服上述问题的缺陷，剔除各模态间的方差差异，Zhang[18]等提出近邻差分算法，对于样本xi先找到它的第k个近邻样本xi,k，进行DIF得到

(3)

再运用同样的方法，找到样本xi,k的第k个近邻样本xi,kk，再进行一次DIF得到

(4)

利用两次DIF消除数据的多中心结构，同时保持当前样本与其近邻之间的位置信息.为了描述数据的空间结构差异，定义样本xi的二阶差商(second order difference quotient，SODQ)如下：

(5)

根据公式(5)运算后，不仅消除了数据的多模态特性，同时消除了各模态间的方差差异.同样利用SODQ方法对以上数值例子进行数据预处理,得到的数据散点图如图4所示.从图4看出，SODQ可以将原始数据的多模态特征和方差差异消除，同时能够分离出密集模态的微弱故障.

1.3 基于二阶差商kNN的多模态过程故障检测方法

基于SODQ-kNN的多模态过程故障检测方法由建模过程和在线检测两部分构成.

(1) 建模过程

(2) 故障检测

① 新来的测试数据xnew，在训练样本中寻找其k近邻样本xnew,k，再寻找样本xnew,k的k近邻样本xnew,kk，进行SODQ运算.

② 用SODQ矩阵代替测试数据来确定统计量d.

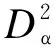
2 仿真结果与分析

2.1 多模态数值例子

利用一个多模态数值例子[19]来验证SODQ-kNN算法对模态间离散程度较大的多模态工业过程检测的有效性.产生数据的模型为：

(6)

其中e1、e2和e3均为服从[0，0.01]分布的白噪声.

模态1：s1和s2为[5，0.1]的正态分布.

模态2：s1和s2为[-5，0.5]的正态分布.

在每个模态中分别生成100个数据集，作为原始训练数据集.再从每个模态中生成100个样本，组成校验测试数据集.通过在变量上设置偏移产生6个故障点组成故障集.图5为数据分布散点图.从图5可以看出，其为各模态间离散程度较大的多模态实例，其中编号为f1、f2和f5的故障数据靠近密集模态.

图5 多模态数据散点图Fig.5 Scatter plot of multimodal data

分别用PCA、kNN、PC-kNN和SODQ-kNN方法对以上数据集进行故障检测，结果如图6所示.其中:PCA和PC-kNN方法的主元个数通过累计贡献率确定，主元个数为7；在kNN中，近邻数k=3；在SODQ-kNN中，选取近邻样本k=3.从图6可以看出:在PCA算法中，SPE统计量检测样本时有4个漏报，8个误报；T2统计量也有4个漏报，8个误报.在kNN算法中，有3个样本漏报，8个误报.在PC-kNN算法中，有3个漏报，10个样本误报.在SODQ-kNN算法中，没有出现漏报，在误差允许范围内出现4个误报.将SODQ-kNN与PCA、kNN和PC-kNN方法进行对比可以看出，SODQ-kNN故障检测率最高，误报率最低，验证了SODQ-kNN算法的优越性.

图6 四种方法对多模态数据的检测结果Fig.6 Detection results of four methods for multimodal data

2.2 半导体生产过程数据

半导体仿真平台[20-21]作为一个典型的时变、非线性和多模态间歇过程，被广泛应用于工业过程故障检测领域.生产过程数据由3个模态组成，其中包括107个正常批次和20个故障批次.在每个模态中分别选取32个批次建模，其余正常批次作为校验批次，因此建模批次为96个，正常校验批次为11个，故障批次为20个.在 21个测量变量中选取 17个变量作为过程检测变量，如表1所示.

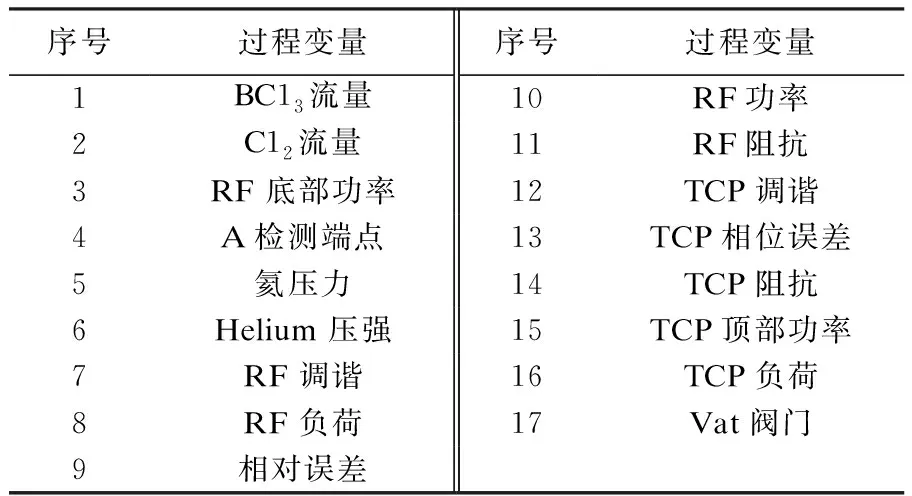
表1 半导体生产过程所用的检测变量Table 1 Detection variables used in semiconductor manufacturing process

数据集中EndPt A变量如图7所示.从图7可以看出:每个批次是不等长的，持续时间在95～112 s变化，根据最短长度法获得等长批次.为了消除初始波动对传感器的影响，去除开始的5个样本，保留85个样本适应最短的批次.将三维建模数据X(96×85×17)沿批次方向展开成二维数据矩阵,得到X(96×1445).同样，将校验数据和故障数据也展开成二维数据矩阵.

图8是半导体数据的前两个主元空间分布图.从图8可以看出:数据分布在不同的区域内，故障3和故障9可以看成是密集模态的虚弱故障，kNN和PC-kNN很难检测出这类故障.

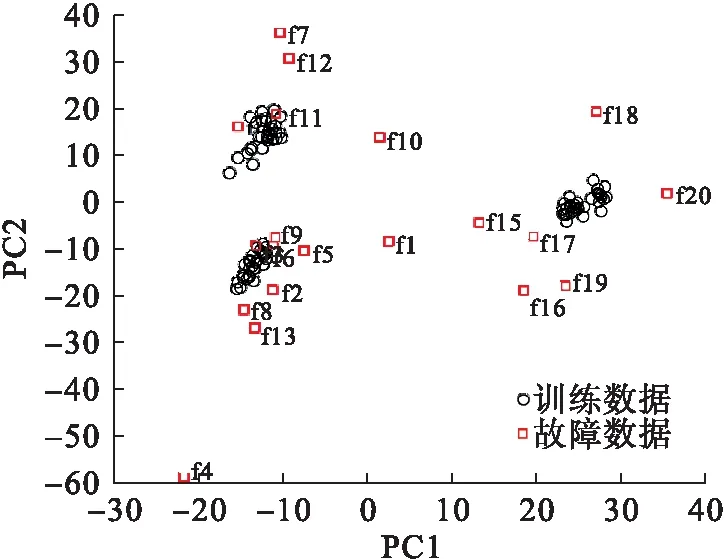
图8 主元空间分布散点图Fig.8 Scatter plot of data distribution in principal component space

对二维数据矩阵分别运用PCA、kNN、PC-kNN 和SODQ-kNN方法进行建模，并对11个校验批次和20个故障批次数据进行故障检测.PCA和PC-kNN方法的主元个数由累计贡献率决定.在kNN中，近邻数k=3；在PC-kNN中，近邻数k=5；在SODQ-kNN中，近邻数k=3.四种方法的检测结果见图9，图中虚线代表95%控制限.从图9可知:PCA的SPE统计量检测出17个故障数据，5个校验数据出现误报；T2统计量没有出现误报，而故障数据仅检测出5个.kNN算法没有出现误报，但是故障数据仅检测出16个.PC-kNN算法没有出现误报，故障数据也仅检测出16个.SODQ-kNN算法没有出现误报，检测出全部故障.与PCA、kNN和PC-kNN算法相比，SODQ-kNN算法的检测效果最好，验证了基于二阶差商kNN算法在方差差异明显的多模态过程故障检测中的有效性.

图9 四种方法对半导体数据的故障检测Fig.9 Fault detection of semiconductor data by four methods

现用PCA、kNN、PC-kNN 和SODQ-kNN方法对96个批次进行建模，并对11个校验批次和20个故障批次数据进行检测.在PCA和PC-kNN方法中，其主元个数根据累计贡献率决定，主元个数为3.在kNN方法中，选取近邻数k=3；在PC-kNN算法中，选取近邻数k=5；在SODQ-kNN中，近邻数k=3.表2 是四种方法对半导体数据的检测结果对比.由表2可以看出：PCA算法的SPE检测指标故障检测率较高，但是其误报率也相对较高；T2检测指标没有误报，但其故障检测率较低，效果不如SODQ-kNN算法.SODQ-kNN算法和kNN算法均没有误报，但是SODQ-kNN算法的故障检测率要高于kNN算法.PC-kNN算法没有误报率，但是未检测出全部的故障.综上所述，与其他三种算法对比，SODQ-kNN算法在没有误报的情况下，故障检测率最高，说明该方法在工业过程的故障检测中具有很好的检测效果.

表2 四种方法对半导体数据的检测结果对比Table 2 Comparisons of detection results of four methods for semiconductor data

3 结 论

研究SODQ-kNN在多模态过程故障检测中的应用.该方法先对数据进行一次DIF运算，去除数据的多中心，再进行SODQ运算，去除多模态数据之间的方差差异，建立kNN模型，克服传统kNN的局限性，提高故障检测性能.用数值例子和实际的半导体实例进行检验，仿真实验可以看出，与其他方法相比，SODQ-kNN算法可以有效地降低漏报率和误报率，证明了该方法的有效性.